基于Kriging方法的整流罩氣動外形設計優化①

楊希祥，周 張，彭 科

(1.國防科技大學航天科學與工程學院，長沙 410073;2.北京理工大學 宇航學院，北京 100081)

0 引言

氣動外形設計在運載火箭總體設計中占有極其重要的地位。運載火箭外形一般由頭部、箭身和尾舵(小型運載火箭)等部分組成。頭部外形設計即整流罩外形設計對飛行性能影響至關重要，是外形設計的關鍵［1］。運載火箭總體設計需重點考慮的氣動阻力、表面傳熱特性和有效載荷容積等因素，都與整流罩外形息息相關。整流罩外形設計在國外飛行器設計中歷來受到高度重視［2－4］，國內卻鮮有文獻對這一問題進行研究。

氣動外形設計優化過程往往需要多次調用氣動參數計算模型，直接采用高精度計算模型將面臨嚴重計算復雜性問題，近似建模方法應運而生。近似建模方法基本思想是用一個簡單逼近函數近似替代復雜高精度實際性能分析模型。根據近似函數所能模擬設計空間的大小，近似建模方法可分為局部近似方法、全局近似方法和中等范圍近似方法。全局近似方法中的Kriging函數法以具有樣本點處無偏估計、良好的高階非線性擬合能力和靈活的近似模型參數選擇等優點，在近似建模領域得到廣泛應用。Meunier和Laurenceau 等采用其建立機翼氣動力近似模型［5－6］;Han等提出一種基于Kriging函數的變復雜度近似建模方法，并應用于氣動力近似建模［7］;Ahmed等分別研究了Kriging函數在高超聲速鈍錐體氣動力和氣動熱近似建模中的應用［8］。

本文研究小型運載火箭整流罩氣動外形設計優化問題，近似模型構造選用Kriging函數法。

1 Kriging函數法及其仿真實現

1.1 參數估計與預測

假定n維輸入變量X與輸出響應y之間的函數關系y(X)未知，給定組s訓練樣本數據(X，y)=［(X1，y1)，…，(Xs，ys)］T，結合線性回歸參數模型和隨機過程非參數模型，采用Kriging函數可構造y(X)的近似模型 y^(X)如下［9］:

式中 fT(X)=［f1(X)，…，fe(X)］為回歸函數;β=［β1，…，βe］T為回歸系數;z(X)為隨機過程。

工程應用中，線性回歸參數模型常采用二階多項式回歸函數，

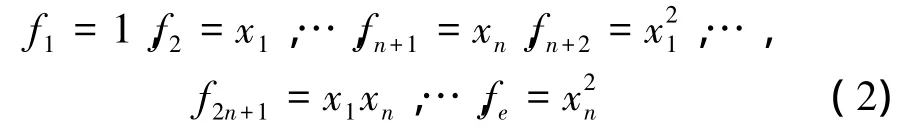
隨機過程非參數模型考慮為真實響應與假設線性模型的偏差，常采用均值為零、高斯相關函數的隨機過程模型，其協方差函數為

隨機變量 y=y(X)和 Ys=［y(X1)，…，y(Xs)］T服從如下多元正態分布:

其中:

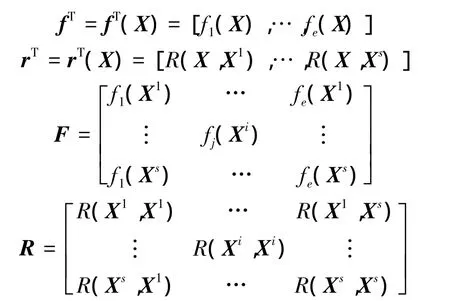
式中 fT為e維回歸函數行向量;rT為s維相關函數行向量;F為s×e維回歸函數矩陣;R為s×s維相關函數矩陣。

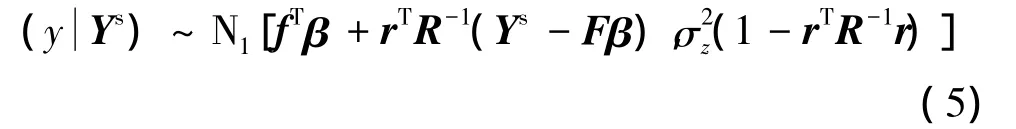
y Ys服從如下條件分布:給定訓練樣本數據Ys下，y的最小均方誤差估計為yYs的條件均值:

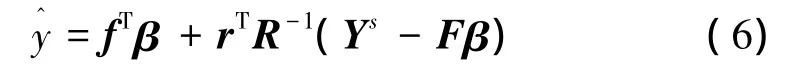
要得到式(6)的Kriging函數近似模型，需基于訓練樣本數據估計近似模型參數β、θ，通常采用兩步估計法，β與θ相互獨立，即滿足下式:

第一步估計是假定已知相關函數模型及參數θ，得到β的廣義最小二乘估計(θ):

第二步估計是得到θ的某個估計θ^，然后將θ^代替θ，得到β^(θ^)作為β的估計。相關參數θ的估計方法有交互驗證估計方法和極大似然估計方法，訓練樣本點數較少時，可選擇交互驗證估計方法，否則選擇極大似然估計方法。

相關參數θ的交互驗證估計值θ^為所有樣本訓練點處的均方預估誤差的最小值點:

采用極大似然估計方法時，假設訓練樣本Ys=［y(X1)，…，y(Xs)］T服從多元正態分布:

取似然函數FMLE為訓練樣本數據Ys概率密度f(Ys):

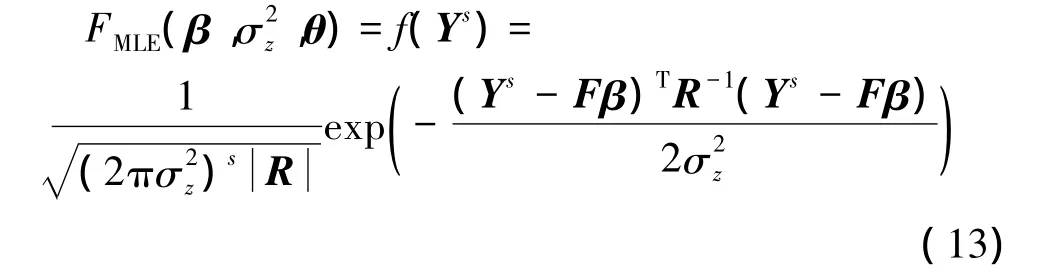
不考慮常數項的對數似然函數為

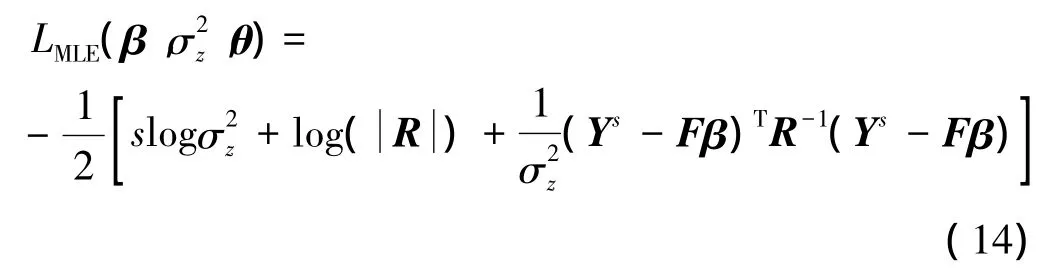
將式(15)代入式(14)，得到只與相關參數θ相關的對數似然函數:

式(18)所示的近似模型不僅可以預估輸入變量X和輸出響應關系y(X)，而且還可以預估輸入變量X處一階偏導數:

1．2 仿真實現

實際應用中，由于訓練樣本數量大，致使高維相關函數矩陣的求逆運算計算復雜，同時訓練樣本點選擇不合理會導致相關函數矩陣病態，無法計算逆矩陣。由于相關函數矩陣對稱，屬稀疏矩陣，為避免直接計算產生較大計算誤差，對相關函數矩陣進行Cholesky分解;為避免不同的設計變量量級不同產生計算誤差，對訓練樣本數據進行標準化處理，具體步驟如下:

(1)對訓練樣本數據進行標準化處理，得到標準空間［－1，1］s上的訓練樣本數據

(4)對回歸函數矩陣F進行正交轉化并做QR分解:QG=C－1F。

(5)計算基于標準化訓練樣本數據的Kriging函數近似模型:

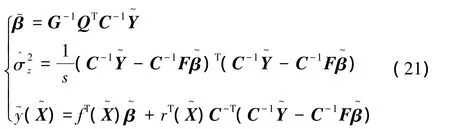
(6)計算式(11)均方預估誤差值fCV(θ)或式(17)對數似然函數值LMLE(θ)。

(7)更新相關參數比例參數θ，重復執行步驟(3)～(6)，直到找到目標函數極小值。

(8)基于訓練樣本數據的Kriging近似模型:

2 整流罩氣動外形設計優化問題

2．1 設計變量選取

研究的運載火箭整流罩前罩基線外形如圖1所示。為靈活表示整流罩氣動外形，便于選取控制變量，采用易修改性和局部調整特性好的非均勻有理B樣條曲線(Non-Uniform Rational B-Spline，NURBS)對整流罩外形進行參數化表示。

控制點選取如圖2所示，除首末2點外，另取4個控制點，共6個控制點。其中，控制點2和控制點1具有相同橫坐標(均為0)，目的是保持NURBS曲線光滑性，控制點3距離頭部頂點很近，目的是增強外形多樣性，控制點5與控制點6具有相同縱坐標，目的是保持后端光滑性［4］。根據NURBS曲線性質，改變控制點坐標即可方便調整整流罩外形，為此，選取控制點坐標為設計變量，共4個，具體如下:控制點3的橫、縱坐標分別為x1和x2，控制點4的縱坐標為x3，控制點5的橫坐標為x4，即控制變量:

圖1 整流罩基線外形Fig.1 Primary shape of fairing

圖2 控制頂點選取Fig.2 Selection of control points

設計變量邊界值的確定對優化設計速度和結果有重要影響。為加快收斂速度，同時確保得到全局最優解，首先采用DATCOM氣動特性工程估算程序與Fay和Riddell熱流密度計算公式，結合Powell法，求得粗略最優解，用于收縮設計空間，然后采用基于Kriging函數近似模型的方法進一步精確求解。

DATCOM是美國空軍實驗室研究的一套用于導彈氣動力工程估算的程序，對整流罩這樣的標準細長體預估誤差在10%～15%，對DATCOM源程序進行校核和修正，形成核心計算程序，編制輸入輸出文件，嵌入優化流程對迭代過程氣動力進行計算。Fay和Riddell熱流近似計算公式用于求解軸對稱體駐點區熱流密度:

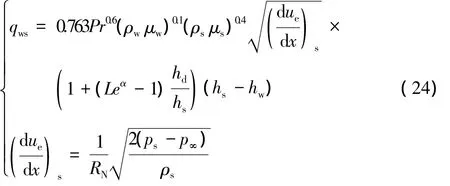
式中 下標w、e、s分別表示壁面條件、邊界層外緣條件、駐點條件;qws為駐點熱流密度;ρw、ρs為密度;μw、μs為粘性系數;hs、hw為比焓;hd為離解比焓;RN為鈍頭半徑。

為便于計算，Le和hd用下式近似計算［10］:

2.2 目標函數和約束條件

運載火箭大氣層飛行段阻力對運載能力有重要影響，而氣動阻力主要集中在頭部。為此，以一級飛行段平均阻力最小為目標函數，選取基線方案3個典型彈道特征點，阻力系數最大點、動壓最大點和一級發動機關機點，3點相關參數如表1所示。

表1 彈道特征點參數Table 1 Trajectory characteristic parameters

引入加權因子對目標函數進行處理，約束條件包括3個設計點駐點熱流密度最大值、整流罩內部容積及設計變量約束:

式中 Di、qwi(i=1，2，3)分別表示設計點i阻力和駐點熱流密度;qw，max為允許熱流密度最大值;V表示整流罩內部容積;Vb表示基線方案整流罩容積值，設計變量邊界根據初步優化值和設計變量實際允許的邊界值得到。

3 設計優化結果與分析

采用Kriging函數建立運載火箭整流罩氣動性能計算近似模型，采用正交表型均勻拉丁超立方試驗設計方法［11］選取樣本點，樣本點選取36個。

樣本訓練采用非結構網格和基于N-S方程的數值計算方法，湍流模型采用k-ε兩方程模型，空間離散采用上風差分格式中的通量差分分裂(FDS)格式，時間分裂采用LU-SGS方法，由于3個特征設計點訓練樣本總數較多，采用并行計算產生氣動力參數。優化方法選取Powell法，初值設定采用2.1節所述方法。

式(25)中，w1、w2和 w3分別取為 0.2、0.5、0.3。經4次迭代優化過程收斂，優化方案目標函數和約束條件如表2所示，表中同時給出了基線方案和在3個特征點分別以阻力最小為目標函數設計結果對應的目標函數和約束條件值。

優化前后整流罩外形(含計算網格)對比如圖3所示。

特征點2處，優化方案和基線方案表面壓力和熱流分布對比如圖4所示。

表2 整流罩外形優化設計結果Table 2 Optimization design results of fairing shape

圖3 基線方案與優化方案外形對比(含計算網格)Fig.3 Comparison of shape between basic scheme and optimal scheme(computation grid)

圖4 基線方案和優化方案軸向參數分布對比Fig.4 Comparison of axial parameters between basic scheme and optimal scheme

由圖4可見，由于頭部鈍度減小，優化方案在頭部具有更小表面壓力，但在距頭部約45～650 mm處，優化方案表面壓力大于基線方案;優化方案母線光滑過渡，表面壓力分布脈動較小，有利于整流罩結構設計;由圖4還可看出，頭部鈍度減小使得優化方案駐點熱流密度較高，但滿足設計約束。

4 結論

(1)采用Kriging函數建立整流罩氣動參數計算近似模型，可有效避免整流罩氣動外形設計優化計算復雜性問題，在保證優化精度的前提下，實現較高的優化效率。

(2)采用建立的整流罩氣動參數計算近似模型，實現了運載火箭整流罩氣動外形設計優化問題，優化方案平均阻力比基線方案減小22.2%，各項約束條件得到良好滿足。

(3)研究成果對于方案論證與方案設計階段飛行器氣動外形設計優化研究具有重要借鑒意義。

［1］龍樂豪.總體設計(上)［M］.北京:宇航出版社.1989.

［2］Lee Young Ki，Lee Jae-Woo，Byun Yung-Hwan.The design of space launch vehicle using numerical optimization and inverse method［C］//17th AIAA Applied Aerodynamics Conference.Norfolk，VA，1998:757-767.

［3］Deeppark N R，Ray T，Boyce R R.Evolutionary algorithm shape optimization of a hypersonic flight experiment nose cone［J］.Journal of Spacecraft and Rockets，2008，45(3):428-436.

［4］Lee Jae-Woo，Min Byung-Young，Byun Yung-Hwan，et al.Multipoint nose shape optimization of space launcher using response surface method［J］.Journal of Spacecraft and Rockets，2006，43(1):137-146.

［5］Meunier M.Simulation and optimization of flow control strategies for novel high-lift configurations［J］.AIAA Journal，2009，47(5):1145-1157.

［6］Laurenceau J，Sagaut P.Buliding efficient reponse surfaces of aerodynamic functions with Kriging and Cokriging ［J］.AIAA Journal，2008，46(2):498-507.

［7］Han Z H，Ralf Z，Gortz S.A New Cokriging method for variable-fidelity surrogate modeling of aerodynamic data［C］//48th AIAA Aerospace Sciences Meeting.Orlando，Florida，2010:1-17.

［8］Ahmed M Y M，Qin N.Metamodels for aerothermodynamic design optimization of hypersonic spiked blunt bodies［C］//48th AIAA Aerospace Sciences Meeting.Orlando，Florida，2010:1-17.

［9］Matheron G.Principles of geostatistics［J］.Economic Geology，1963(58):1246-1266.

［10］王國雄.彈頭技術(上)［M?.北京:宇航出版社，1993.

［11］張潤楚，馬長興.正交表型均勻LH設計和抽樣［J］.應用概率統計，2001，17(3):243-254.