考慮UPFC安裝位置的靜態電壓穩定分析

高 松，高運泉

(1.東北電力大學電氣工程學院，吉林吉林132012;2.吉林建筑大學城建學院，長春130111)

目前，電力系統采用超高壓遠距離輸電和大型區域電網互聯［1］，使系統處在電壓穩定裕度很低的工作點上運行。對此，國內外學者對靜態電壓穩定問題已經進行了較為深入的研究，文獻［2］基于擴展潮流方程雅克比矩陣的特征結構分析法，提出了一種確定大規模電力系統電壓失穩區的計算方法;文獻［3］提出了運用特征結構分析法進行靜態電壓穩定性分析，通過節點參與因子和節點靈敏度指標確定了弱穩定區域;文獻［4］是基于特征結構分析法探討了風電場接入系統后對系統電壓穩定性的影響，并在系統中安裝FACTS裝置提高電壓穩定性;文獻［5］提出了一種用TCSC提高交直流系統的靜態電壓穩定性的方法;文獻［6］采用自適應遺傳算法和連續潮流法結合，進行了計及統一潮流控制器作用的靜態電壓穩定裕度計算;文獻［7］判斷了全電網最有可能發生電壓不穩定的節點和區域，并采用STATCOM提高靜態電壓穩定。而UPFC是FACTS裝置中功能最強大的器件，上述文獻沒有將UPFC與電壓穩定問題相結合，沒有考慮UPFC的安裝位置對靜態電壓穩定的影響，因此，本文建立了UPFC的節點等效注入功率模型，并運用特征結構分析法對當前系統運行狀態進行靜態電壓穩定分析及UPFC的潮流計算找出系統薄弱環節，改善了系統的電壓穩定裕度。

1 UPFC的節點等效注入功率模型

UPFC(統一潮流控制器)由兩個共用直流側電容的背靠背電壓源換流器構成。其中一個換流器通過變壓器串聯接入系統，向線路注入一幅值和相角可調節的串聯電壓，以控制線路的潮流，在系統中可等效為一個串聯電壓源UT。另一個換流器通過變壓器并聯接入系統，該換流器可以通過變壓器向系統吸收或注入無功功率，在系統中可等效為一個并聯電流源Ish;向串聯側的換流器提供有功功率，使裝置與系統總的有功交換為零，從而維持直流側電容兩端的電壓恒定［8－10］。

假設在線路i－j的節點i側加入UPFC裝置，其等效電路模型如圖1所示，并聯電流源可分解成與Ui同相的有功分量It和與Ui正交的無功分量Iq。

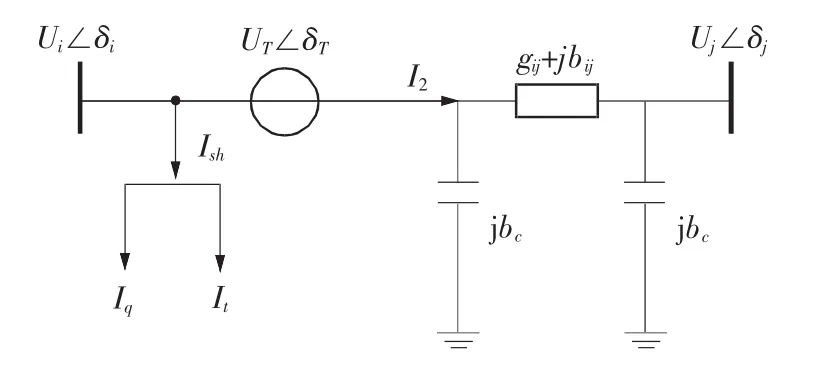
圖1 UPFC的等效電路圖Fig.1 Equivalent circuit of UPFC

采用等效功率注入法將UPFC嵌入電力系統，該方法相當于一種網絡變換，即將UPFC對潮流的控制作用轉移到所在的線路兩側的節點上，如圖2所示，這樣可以不改變原有節點導納矩陣情況下方便地嵌入模型。

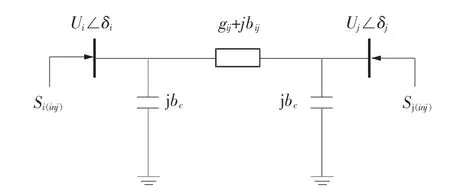
圖2 UPFC的等效注入功率模型Fig.2 UPFC’s equivalent injected power model

通過一系列的公式整理計算可以得到i、j側的UPFC等效注入功率的直角坐標下的形式:

式中:e、f分別為節點電壓的實部和虛部;eT、fT分別為串聯電壓源 UT∠δT的實部和虛部，即 eT=UTcos(δT)、fT=UTsin(δT)，gij、bij和 bc分別是線路i－j的電導、電納和對地電納。

2 含UPFC的潮流計算

2.1 電力系統潮流方程

在一個電力系統中，假設共有n個節點，其中PQ節點為m個、PV節點為n－m－1個，還有一個平衡節點，則直角坐標系下的潮流方程為

式中:Pis和Qis分別為給定的節點有功注入量和節點無功注入量;Uis為給定的PV節點電壓值;Gij和Bij對應為節點導納矩陣元素的實部和虛部;ei和fi對應為節點電壓的實部和虛部。

2.2 含UPFC的電力系統潮流方程

若線路安裝UPFC時，在潮流計算中原有潮流方程則需增加UPFC等效注入附加功率的影響。假設在線路i－j的節點i側加入UPFC裝置，則僅將UPFC所在線路兩端的i和j兩個節點的潮流方程進行修改即可，而其他節點的潮流方程均不變。i和j兩個節點的潮流方程修改為

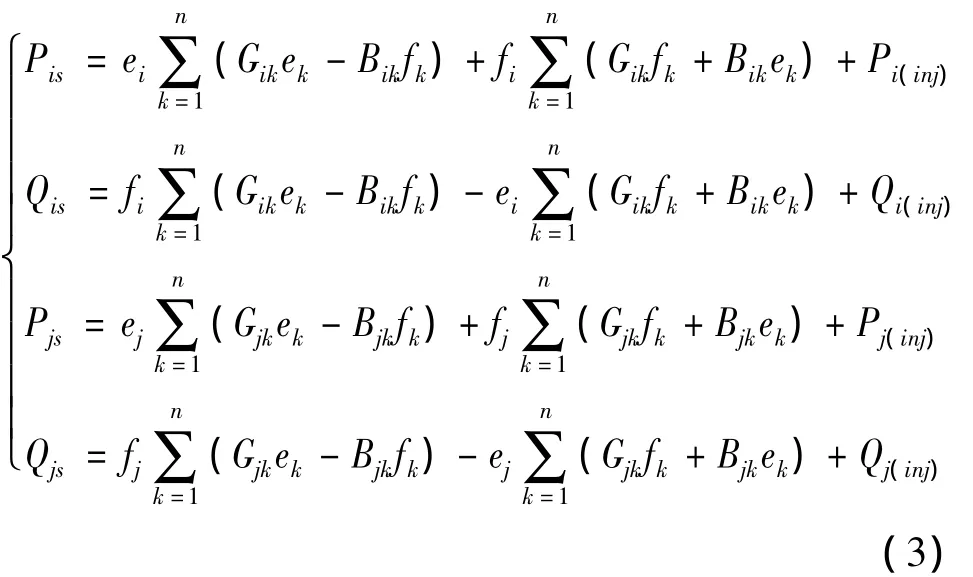
式中:Pis和Qis分別為節點i的有功注入量和無功注入量;Pjs、Qjs分別為節點j的有功注入量和無功注入量;Pi(inj)、Qi(inj)、Pj(inj)、Qj(inj)為 UPFC 的等效注入功率。由于此式的i、j代表的是安裝UPFC線路兩端的節點，故將原潮流方程式的j改為k，從而避免沖突。

2.3 含UPFC的潮流計算中雅克比矩陣的修正

當系統中加入UPFC時，由式(1)可知，UPFC的等效注入功率是關于節點電壓的方程，因此在進行系統潮流計算時，需要對關于節點i和節點j的雅克比矩陣元素進行修正，而原矩陣中關于其他節點的元素不變。記雅克比矩陣的形式

則修正量如下:

對于節點i，有

對于節點 j，有

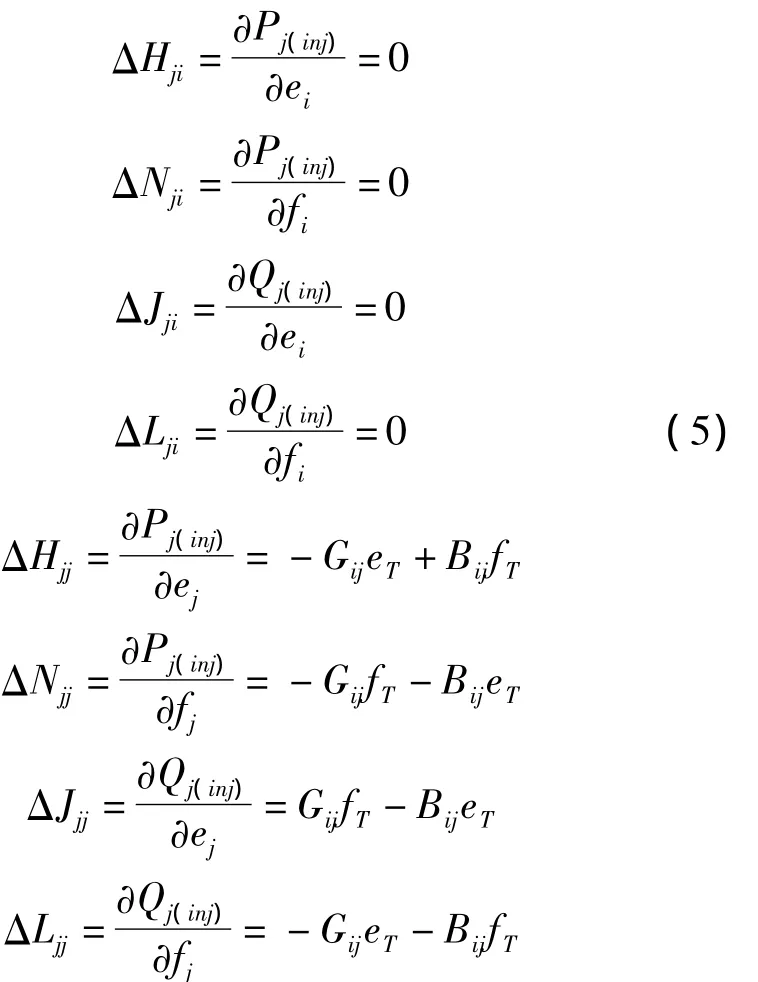
3 靜態電壓穩定分析

3.1 電壓穩定性的特征結構分析法

應用特征結構分析法進行靜態電壓穩定性分析的實質就是對潮流雅克比矩陣的特征結構進行分析。該方法首先對潮流方程取偏差量進行攝動分析，如式(6)表示了一個矩陣形式的線性關系:

把注入向量的攝動量ΔYs和狀態向量的偏差量ΔX表示成Jr的右特征向量基的形式:

式中:αi、βi分別為 ΔYs和 ΔX 與右特征向量 Ui間的標量耦合系數。又根據如下關系

可以求得耦合系數間的關系:

那么，將式(14)、式(11)代入式(9)可以得到:

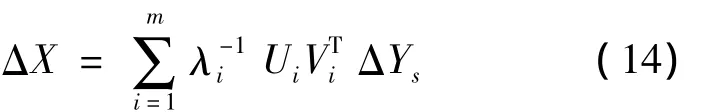
根據電力系統的特點，當系統的運行從正常狀態向其靜態穩定的極限過渡時，雅克比矩陣會向著奇異方向變化，會有一特征值首先通過零點，因其模為最小，故稱為最小模特征值，記作λmin。當雅克比矩陣奇異時，則λmin=0，那么此時觀察式(14)，只要是‖ΔYs‖不為零，無論多小，都要使狀態向量無限漂移，即‖ΔX‖趨向于無窮大，顯然此時達到了系統靜態穩定的極限。可以用λmin的大小來度量系統工作點的靜態穩定裕度，λmin越小，所引起的狀態量變化就越大，當前系統電壓穩定性越差［11］。

為了準確地確定系統電壓薄弱環節，本文采用基于特征結構譜分解的狀態變量對特征模式的參與因子指標，該參與因子可指示與特征模式強相關的主要節點。參與因子矩陣如下:

式中:pki為第k個狀態變量對第i個特征根λi的參與因子;uki為λi對應的右特征向量的第k個元素;vki是λi對應的左特征向量的第k個元素。

通過進一步推導可以得出第k個節點電壓靈敏度為

當無功功率變化方向與λmin對應的右特征向量方向一致時，會導致系統狀態變量發生最大變化，該變化方向對應系統最容易發生失穩的方向，故通過比較特征模式為λmin下的參與因子pkmin的大小，可以很好地確定與最小模特征值強相關的主要節點［12］。綜合分析節點參與因子pkmin和各節點電壓靈敏度數據，即可找到全系統最薄弱的節點或區域。

3.2 考慮UPFC的靜態電壓穩定分析步驟

考慮UPFC的靜態電壓穩定分析步驟如下:

1)利用牛頓－拉夫遜法的最優乘子法進行潮流計算得到系統狀態雅克比矩陣。利用反冪法原理計算其最小模特征值，求出其相應的左、右特征向量。

2)計算以最小模特征值λmin為特征模式下的節點參與因子以及各節點電壓靈敏度，找出系統的薄弱環節。

3)設置適當的 UPFC的控制參數，并將該FACTS控制器分別在最薄弱環節和一般薄弱環節處安裝。

4)再次求取電壓穩定裕度λmin，驗證UPFC提高電壓穩定性的作用，以及UPFC的不同安裝位置的效果。

4 算例分析

本文采用新英格蘭39節點系統進行算例分析。設節點2為平衡節點，其余發電機節點均為PV節點。對該系統在正常運行狀態下進行仿真計算，在得到的計算結果中，抽取了該系統中的17個節點數據，這些節點擁有較大的最小模特征值λmin對應的參與因子pkmin和較大的電壓靈敏度，整理如表1所示，其中的數值均為標幺值。

對表1數據的參與因子和電壓靈敏度結果的大小進行比較，參與因子越大，該節點越容易出現失穩，而電壓靈敏度越大，則該節點越不穩定。將系統薄弱節點的順序(由弱到強)排列和計算得到的系統電壓穩定裕度結果整理如表2所示，其中的數值均為標幺值。

通過表2可以看出，由參與因子指標與節點電壓靈敏度指標確定的薄弱節點順序有一些差異，但兩種指標確定的最薄弱節點都是節點17，故該系統的節點17最容易出現電壓失穩。

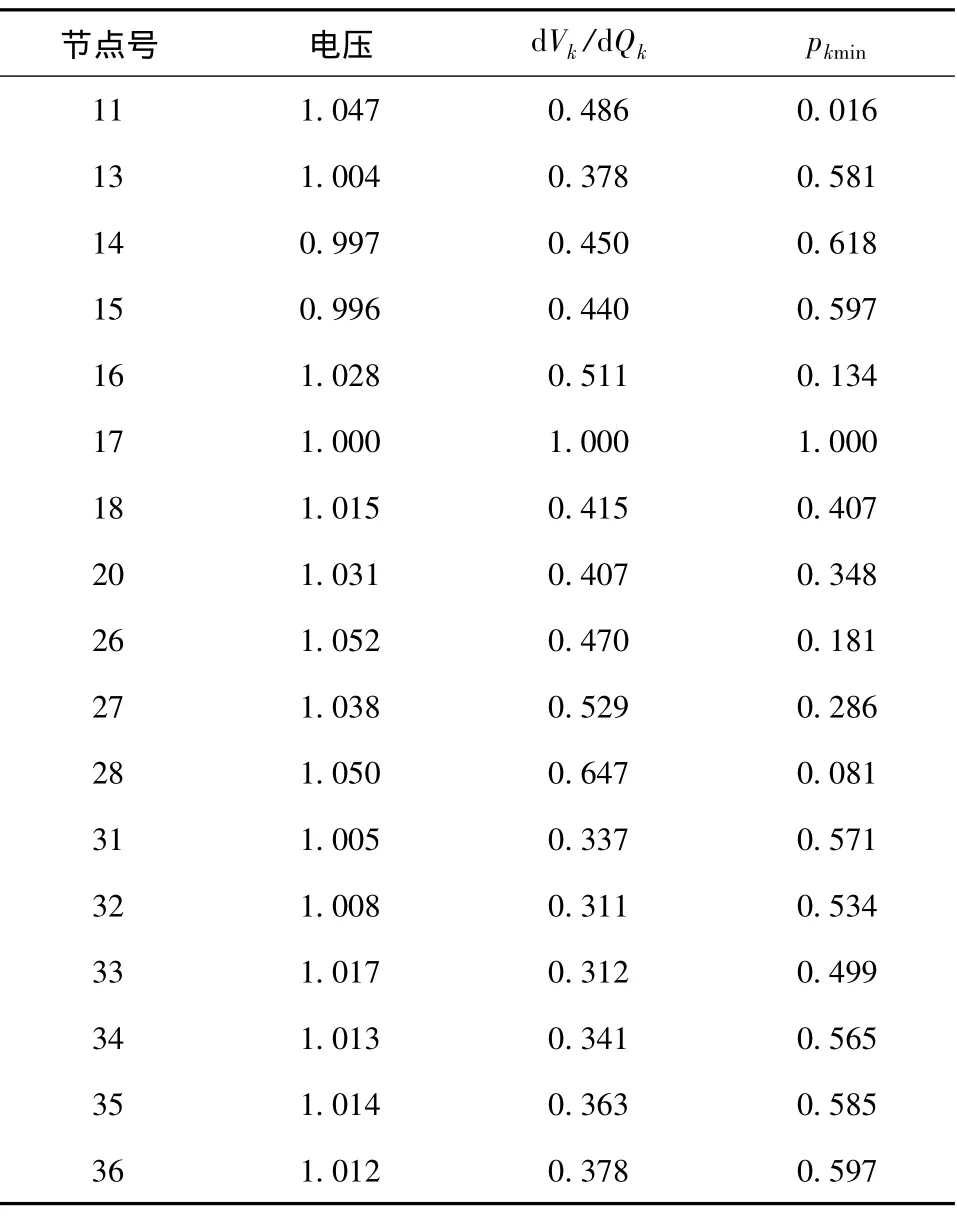
表1 根據計算結果抽取的17個節點的綜合數據Tab.1 Comprehensive data of extracting17 node according to calculation results

表2 由不同指標確定的薄弱節點排序及系統電壓穩定裕度Tab.2 weak node order and voltage stability by different indicators margin to determine

為了提高系統的電壓穩定性，本文考慮將UPFC安裝到系統中，同樣在新英格蘭39節點系統進行算例計算，通過適當調整UPFC的控制參數，以及安裝位置，驗證UPFC對系統電壓穩定性的影響。經過測試，當UPFC的控制參數為串聯環節的電壓幅值 UT=0.121(p.u.)，相角 δT=79.15°，并聯環節的電流無功分量Iq=0.141(p.u.)時，可以有效地提高電壓穩定(此參數是否為最優控制參數不是本文研究的重點)。在UPFC安裝在標準測試系統的一般薄弱的節點處進行測試，根據表2的薄弱節點順序選取薄弱程度較靠后的線路20－37的節點20處;再將UPFC安裝在最薄弱節點，即線路17－34的節點17處，經過計算得到結果如表3所示，其中的數值均為標幺值。

表3 不同位置安裝UPFC的穩定裕度及全網最低節點電壓Tab.3 Stability margin and the lowest whole network node voltage of UPFC installed at different positions

由表3可以看出，系統安裝UPFC后電壓穩定裕度λmin和全網最低的節點電壓均有了一定的提高，其中在最薄弱節點17處安裝UPFC，系統的電壓穩定裕度和最低節點電壓提高最為顯著，從而證明了在最薄弱節點位置安裝UPFC可以更好地提高電壓穩定性。

5 結論

1)采用等效注入功率模型將UPFC嵌入電力系統，僅對潮流計算中的雅克比矩陣進行修改即可，不需要改變原有節點導納矩陣，并可使UPFC的控制變量(UT的幅值和相位、Ish的有功和無功分量)從 4 個減少為 3 個(UT，δT，Iq)，降低了一些工作量。

2)運用特征結構分析法對當前系統運行狀態進行靜態電壓穩定分析，找出系統薄弱環節，并在最薄弱節點和一般薄弱節點處安裝UPFC。

3)經過算例驗證，本文提出的方法能較好地改善系統電壓穩定裕度。

［1］ 李娟，劉海龍.動態連續潮流與改進捕魚算法結合計算靜態電壓穩定裕度［J］.華北電力大學學報，2013，40(3):11 －16.LI Juan，LIU Hailong.Calculation of static voltage stability margin based on dynamic continuation power flow and improved optimization algorithm on simulating the fisher’s fishing［J］.Journal of NCEPU，2013，40(3):11－16.

［2］ 馮治鴻，周雙喜.大規模電力系統電壓失穩區的確定方法［J］.中國電機工程學報，1997，17(3):152 －156.FENG Zhihong，ZHOU Shuangxi.Determination of voltage collapse areas in large scale power system［J］.Proceedings of the CSEE，1997，17(3):152 －156.

［3］ 錢俊良，李鵬，陳巧玲，等.基于特征結構分析法的靜態電壓穩定算法［J］.華北水利水電學院學報，2013，34(1):97 －99.QIAN Junliang，LI Peng，CHEN Qiaoling，et al.Static voltage stability algorithm based on eigenvalue structure analysis［J］.Journal of North China Institute of Water Conservancy and Hydroelectric Power，2013，34(1):97 －99.

［4］ 張建平，丁權飛.基于ESA的風電場并網系統靜態電壓穩定性分析［J］.電力系統保護與控制，2010，38(21):33 －38.ZHANG Jianping，DING Quanfei.Analysis of static voltage stability of grid－connected wind farm system based on ESA［J］.Power System Protection and Control，2010，38(21):33 －38.

［5］ 吳杰康，丁一琰，何杲杳.計及TCSC的交直流系統靜態電壓穩定性分析［J］.電網技術，2009，33(11):23 －32.WU Jiekang，DING Yiyan，HE Gaoyao.Static voltage stability analysis of AC/DC power system with thyristor controlled series compensator taken into consideration［J］.Power System Technology，2009，33(11):23 －32.

［6］ 李杰，夏彬.計及統一潮流控制器的靜態電壓穩定裕度計算［J］.電力科學與工程，2012，28(2):32 －36.LI Jie，XIA Bin.Static voltage stability margin calculation considering unified power flow controller［J］.Electric Power Science and Engineering，2012，28(2):32 －36.

［7］ 吳杰康，詹厚劍，齊佳鑫，等.計及STATCOM的電力系統電壓穩定特征結構分析［J］.電力系統及其自動化學報，2009，21(6):1－5.WU Jiekang，ZHAN Houjian，QI Jiaxin，et al.Eigenvalue structure analysis for voltage stability of power system considering statcom installation［J］.Proceedings of the CSU －EPSA，2009，21(6):1－5.

［8］ 武智慧.考慮統一潮流控制器的電力系統優化潮流研究［D］.沈陽:沈陽工業大學碩士學位論文，2013.WU Zhihui.Research on power system optimal power flow considering unified power flow controller［D］.Shenyagn:Shenyang U-niversity of Technology，2013.

［9］ 劉光時.計及統一潮流控制器的電力系統無功優化研究［D］.重慶:重慶大學，2012.LIU Guangshi.Research on power system reactive power optimization considering unified controller［D］.Chongqing:Chongqing University，2012.

［10］ 孫國強，衛志農，李陽林，等.計及統一潮流控制器的電力系統狀態估計［J］.電力系統自動化，2006，30(2):63 －67.SUN Guoqiang，WEI Zhinong，LI Yanglin，et al.The algorithm of state estimation for power systems with unified power flow controllers［J］.Automation of Electric Power System，2006，30(2):63－67.

［11］ 王業庭.基于特征值算法的靜態電壓穩定分析與控制［D］.北京:北京交通大學，2012.WANG Yeting.Analysis and control of static voltage stability based on eigenvalue structure algorithm［D］.Beijing:Beijing Jiaotong University，2012.

［12］ 蔡智慧.考慮靜態電壓穩定性的電力系統多目標最優潮流研究［D］.長沙:長沙理工大學，2008.CAI Zhihui.Research on power system multi－ objective optimal power flow considering static voltage stability［D］.Changsha:Changsha University of Science and Technology，2008.