基于有限元的某汽車排氣系統模態分析及懸掛點的優化

（濰柴動力股份有限公司上海研發中心，上海201315）

基于有限元的某汽車排氣系統模態分析及懸掛點的優化

郭深深，王云英，喬海周

（濰柴動力股份有限公司上海研發中心，上海201315）

在整車開發前期，為了盡可能減小排氣系統懸掛點位置對整車NVH性能的影響，采用有限元分析的方法對某汽車排氣系統的振動模態進行分析，同時利用平均驅動自由度法（ADDOFD）對系統懸掛點位置進行優化。研究結果顯示：在汽車開發前期，采用ADDOFD法進行排氣系統懸掛點位置的優化布置是有必要的。所做仿真分析研究對于縮短整車開發周期、節約成本、優化性能有重要意義。

排氣系統模態分析懸掛點優化有限元分析平均驅動自由度法

1 引言

隨著人們生活水平的提高和汽車工業的不斷發展，人們對汽車的要求也越來越高，結構緊湊、寬敞舒適、NⅤH性能良好的汽車產品普遍受到歡迎。

汽車排氣系統一般通過法蘭和吊耳與發動機歧管及車身底板相連。在汽車的使用過程中，排氣系統由于受到發動機振動和排氣激勵的影響，會產生較大的振動，而振動能量通過懸掛點傳遞至車身底板，引起車身振動并產生車內噪聲。與此同時，在整車開發后期，由于油箱、底板、懸架的布置往往會造成吊耳的懸掛點無法滿足整車NⅤH性能的要求。因此，在整車開發前期對排氣系統振動進行分析，優化吊耳懸掛點的位置，以減少車身振動及噪聲水平，是排氣系統設計時需要重點關注的方面[1,2]。

對排氣系統振動問題的早期研究方法是試驗法，即通過試驗手段進行排氣系統與整車NⅤH性能的匹配，這種方法研究周期長且成本較高。本文利用排氣系統三維數模及質量分布情況，借助有限元分析軟件對排氣系統進行振動仿真及模態分析，在整車開發前期實現吊耳懸掛點位置的優化選擇，降低排氣系統振動對車內噪聲及駕乘舒適性的影響，同時縮短研發周期，降低研發成本，這對整車開發及NⅤH性能的優化具有重要的意義。

2 模態分析理論

2.1模態分析的理論基礎

對于一個n個自由度線性的定常系統，其基本振動方程可寫成[3,4]：

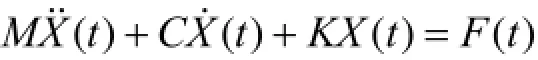
其中，M為系統的質量矩陣，C為阻尼矩陣，K為剛度矩陣，X(t)為加速度向量，X(t)為速度，F(t)為動激勵載荷向量。

機構動力特性分析是屬于經典的模態分析領域，通過分析能確定結構的各階固有頻率、各階振型及阻尼，而結構的固有頻率和振型是分析結構動力學響應及其他動力特性問題的基礎。在進行模態分析時，一般因結構阻尼較小，對固有頻率和振型影響甚微，故通常忽略不計。于是，任何一個無阻尼線性彈性結構振動系統自由振動運動方程可表示為：

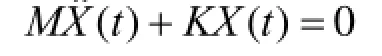
在此情況下，分析結構的固有頻率與振型問題就轉化為求解方程的特征值與特征向量問題。

2.2平均驅動自由度位移法（ADDOFD）

假設單點激勵，由多自由度系統模態分析理論，響應點l和激勵點p之間的頻率響應函數為[5,6]：

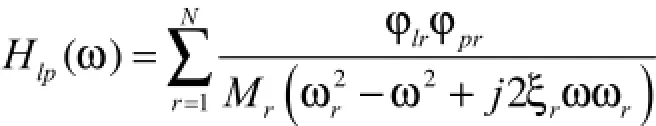
其中，φlr是第l個測點，第r階模態振型系數，Mr和ξr分別是模態質量和模態阻尼比。如果激勵力的頻率為ωr，則近似地有：

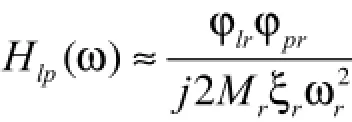
對于線性系統，位移響應的幅值和頻率響應函數的幅值成正比，即

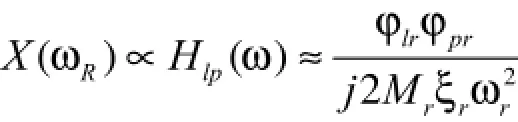
假設振型以質量矩陣歸一化，各階模態阻尼近似相等，則

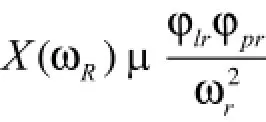
可定義第j個自由度的平均去頂自由度位移（ADDOFD）為

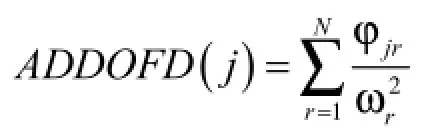
ADDOFD(j)可獲得某個自由度在一般激勵情況下的（在某個頻率范圍內所有模態均被激發）的位移響應相對大小，以此對排氣系統吊耳懸掛點的位置進行優化選擇。

3 某車型排氣系統模態分析

3.1 有限元模型的建立

該車型排氣系統由以下幾部分組成：波紋管、三元催化器、后消音器、排氣管路及聯接法蘭。由于排氣系統結構較為復雜，在建立有限元模型時對系統進行適當程度的簡化：（1）法蘭簡化為體單元；（2）三元催化器及后消音器簡化為集中質量單元，集中質量單元位于三元催化器和后消音器的幾何中心；（3）波紋管簡化為CBUSH彈簧聯接單元。

模型參數如下：三元催化器前法蘭厚度10 mm，三元催化器后法蘭厚度6 mm，三元催化器及后消音器壁厚1.2 mm，其余管路部分厚度均為1.5 mm，材料彈性模量E=2.1×105MPa，泊松比μ=0.3，密度ρ=7.9×10-3g/mm3，CBUSH彈簧單元在X、Y、Z三個方向剛度為Kx=20，Ky=1，Kz=1。有限元模型見圖1。

圖1 排氣系統有限元模型

3.2系統模態分析

不考慮排氣系統原懸掛、支撐及排氣歧管約束對排氣系統振動的影響，對排氣系統自由模態進行分析。通過對自由模態的分析，求解排氣系統固有振動屬性，為整車NⅤH性能匹配提供依據。該車型所配的發動機轉速范圍0～3 300 r/min，通過計算可以得到發動機激勵頻率范圍0～110 Hz。即在自由狀態下只需對0～110 Hz頻率范圍內排氣系統各階模態進行分析。

表1列出了排氣系統各階固有頻率，由于1-9階頻率很小，排氣系統是剛性體，可以認為是離散剛體的固有頻率，其并未顯示在表1中。在發動機0～110 Hz激勵頻率下，僅對10～19階振型進行分析。

選取排氣系統幾個典型自由模態（11階、15階、17階、18階）位移分布云圖見圖2。

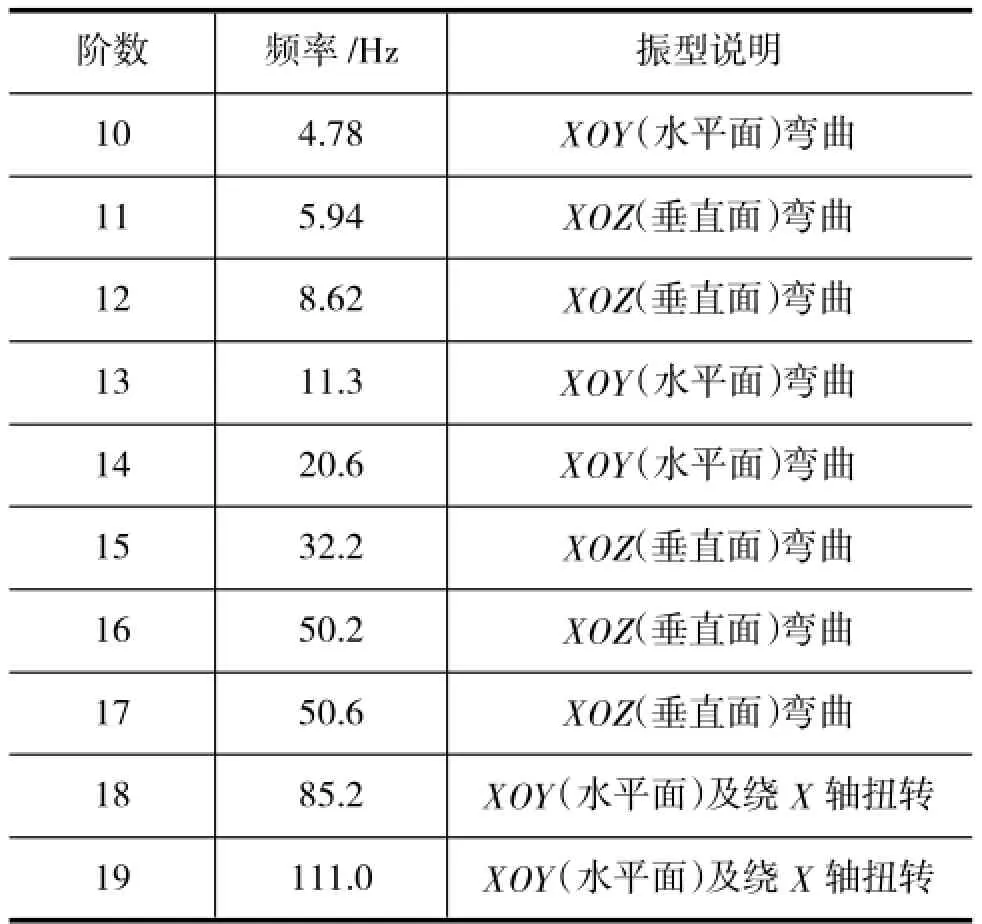
表1 模態分析結果

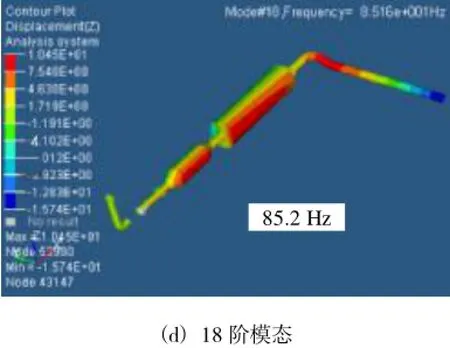
圖2 排氣系統有限元模型

由圖2可以看出，各階模態振動位移各有不同，11階模態的波紋管前位置相對位移較小，而三元催器與后消音器相對位移較大；15階后消音器整體相對位移偏小，尾管拐彎處相對位移較大；17階模態波紋管前段相對位移較大，而尾管相對位移較小；18階波紋管之前相對位移較小，波紋管之后相對位移較大，而且存在扭轉現象。

根據以上模態分析，在選擇最優懸掛點時，因綜合考慮各階模態（11～19階），將懸掛點布置在綜合相對位移較小的位置。

4 排氣系統懸掛位置的優化選擇

4.1懸掛位置選擇的原則

排氣系統懸掛位置選擇一是考慮質量分布，即在系統中的質量集中位置安裝懸掛點，如三元催化器、消音器前/后附近的位置[7]。

其二是懸掛點位于系統XOZ（垂直平面）方向主要振型節點位置。排氣系統彎曲振動主要發生在XOY平面（水平面）及XOZ平面（垂直平面），排氣系統吊掛點垂直安裝的情況下，XOY平面彎曲振動傳遞到車架及車身的振動力影響很小，因此在吊掛點布置時，主要考慮位于XOZ內彎曲振動節點附近。

4.2懸掛點位置的選擇

基于質量分布的懸掛位置選擇原則，在排氣系統中，選擇可能的所有懸掛點位置（包括現懸掛位置），進行標號。該車型排氣系統可能的懸掛位置見圖3，一共13懸掛點位置，其中4、7、8、12為原設計的4個懸掛位置。

根據平均驅動自由度位移法（ADDOFD）計算各懸掛位置在XOZ方向的位移比值，計算結果見圖4。位置點4、7、8、10、13為XOZ方向振動節點位置，即為該車型改進后的排氣系統五個最優懸掛點位置。與原懸掛位置4、7、8、12相比，即在消音器后端增加掛點10，并將尾管處懸掛點12移至靠近尾管出口的懸掛位置13。

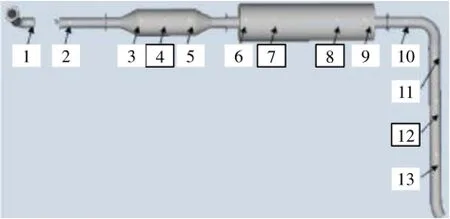
圖3 排氣系統可能的懸掛位置

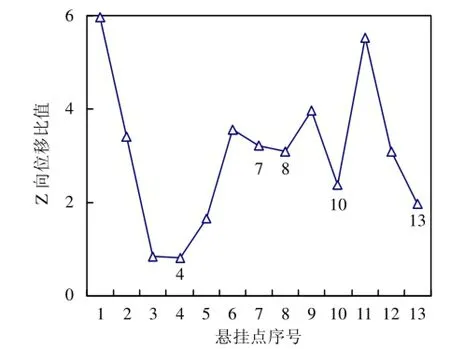
圖4 各懸掛位置Z向位移比值曲線圖

5 懸掛點優化前后車內噪聲測試對比與分析

排氣系統通過法蘭與吊耳與排氣歧管及駕駛室底板連接，由于發動機本身振動及排氣激勵的影響，振動較大并通過懸掛點傳向車身，引起較大的車內噪聲[8]。

參考GB 18697－2002標準，按照圖5中的測點對該車輛進行怠速工況和二檔加速工況車內噪聲測試。測試懸掛點優化前后怠速工況時車內各測點聲壓級，測試結果對比見圖6。

測點4噪聲降幅較大，其二檔加速工況噪聲測試結果見圖7。由圖6、圖7可知，怠速工況下，車內各測點噪聲均明顯降低，其中，后排測點4、測點5噪聲降幅較大。優化后，測點1、測點2噪聲略高于目標值，測點3、測點4、測點5噪聲均優于目標值。

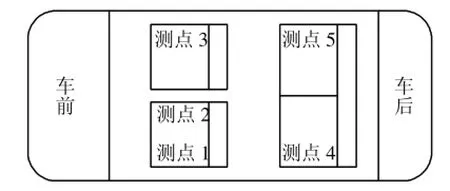
圖5 車內噪聲測點位置示意圖

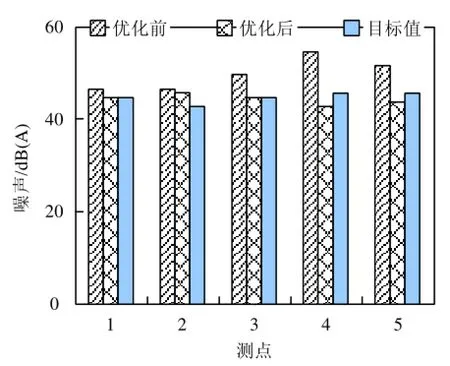
圖6 優化前后怠速工況各測點聲壓級對比

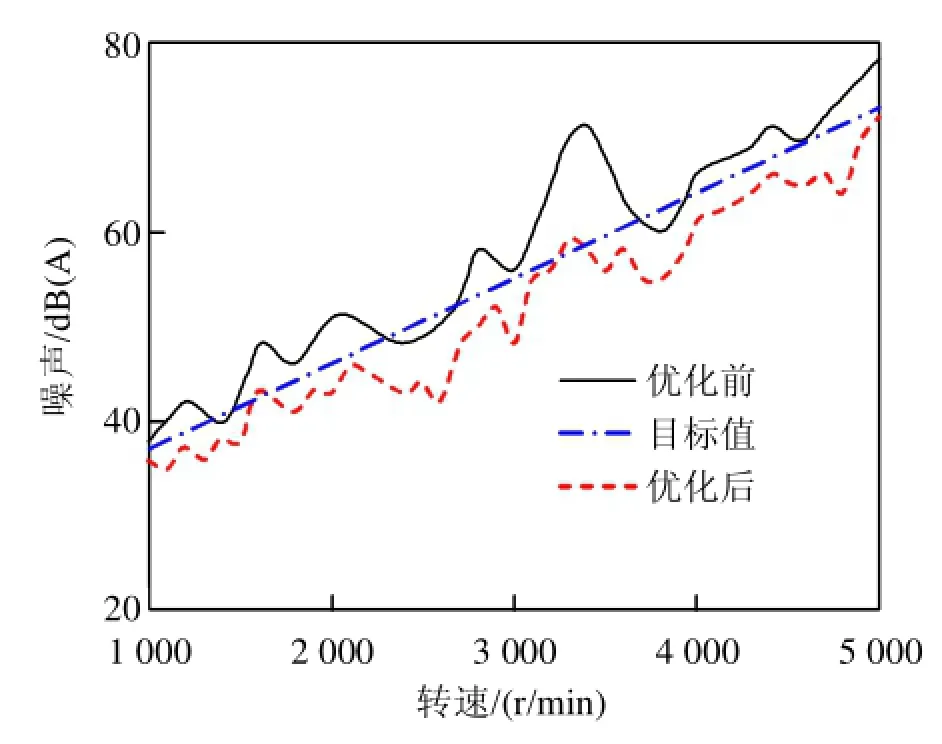
圖7 優化前后二擋加速工況測點4聲壓級對比

在二檔加速工況，測點4優化后的噪聲值下降較多，在測試轉速范圍內，噪聲呈波動式增長，除個別轉速處噪聲值略高于目標值，其余測試轉速區域噪聲優化效果明顯。

6 結束語

本文基于有限元分析的方法對排氣系統進行振動模態分析，獲取系統的固有頻率及振型信息。同時，基于平均驅動自由度位移法（ADDOFD）對排氣系統懸掛位置進行優化選擇，可以在整車開發前期縮短研發周期、降低研發成本，并有助于提高整車NⅤH性能。

采用以上方法對某車輛排氣系統懸掛點進行優化，將懸掛點設置在振動節點處。測試結果顯示，優化后車內噪聲明顯下降。其中，怠速工況時前排車內噪聲平均下降2 dB(A)，后排噪聲平均下降5 dB(A)；二檔加速工況時噪聲平均下降達到4 dB (A)，測試轉速范圍內最大降幅達到6 dB(A)。

1傅志方，華宏星.模態分析理論與研究[M].上海：上海交通大學出版社，2000.

2張勝蘭，鄭冬黎.基于HyperWorks的結構優化設計技術[M].北京：機械工業出版社，2007.

3楊萬里，陳燕，鄧小龍.乘用車排氣系統模態分析數值模擬研究[J].三峽大學學報：自然科學版，2005.

4王繼先，李兆文.內燃機排氣系統振動特性分析[J].內燃機工程，2008.

5趙海瀾，顧彥.汽車排氣系統懸掛點優化[J].計算機輔助工程，2006.

6李松波.車輛排氣系統振動建模與動力學特性研究[D].上海交通大學，2008.

7徐獻陽，李松波，張建武.某轎車排氣系統振動特性仿真及優化[J].設計與研究-機械，2008.

8 Lee C M,Park S T.Development of a Simple Numerical Method of the Exhaust System to Find Optimized Design Values[DO/OL].SAE, 2000(1):0117.

Ⅴibration Model Analysis of Automobile Exhaust System andⅠts Hanging Location Optimization

Guo Shenshen,Wang Yunying,Qiao Haizhou
（Weichai Power Co.,Ltd.,Shanghai R&D Center,Shanghai 201315,China）

Ⅰn order to reduce the impact of exhaust system vibration on vehicle NⅤH performance at the early stage of a vehicle design,finite element analysis is used to perform finite modeling and vibration modal analysis on a vehicle's exhaust system.Furthermore,a method called average driving DOF displacement (ADDOFD)is used to optimize hanging locations.The result suggests that the ADDOFD method is an effective method for determining hanging locations of exhaust system in the early stage of a vehicle design. Therefore,the simulation analysis presented in this paper could save both time and cost in developing a new vehicle.

exhaust system,vibration modal analysis,hanging location optimization, finite element method,ADDOFD method

10.3969/j.issn.1671-0614.2014.04.004

來稿日期：2014-07-14

郭深深（1987-），男，本科，主要研究方向為排氣系統設計及有限元分析。