具有馬爾可夫性的HJM模型下的廣義久期

薛冬梅，劉 巍

(吉林化工學院理學院，吉林吉林132022)

利率是金融市場上最重要的價格變量之一，它直接決定了相關金融產品的定價和利率風險的管理.HJM模型是描述利率隨機行為的連續時間模型，由Heath，Jarrow，Morton于1992年在其發表的論文《債券定價及期限結構:一種新方法》［1］中所提出.它的新穎之處在于:直接從遠期利率期限結構的跨期波動特征入手，設定債券和相關衍生品在有效期內的波動率函數結構，以整條收益率曲線作為狀態變量，根據給定的初始遠期利率曲線精確擬合當前的各種遠期利率曲線，已成為嵌套所有利率期限結構模型的一致框架［2］.

由于久期作為利率風險管理的重要工具，可以準確、有效地衡量利率水平對債券價格的影響，因此為了更好地在利率風險管理中實施有效的風險控制策略，本文研究了具有馬爾可夫性的HJM模型下的廣義久期.

1 HJM模型概述

考慮市場行為在有限時間間隔［0，τ］內發生，市場信息的到達可由一個完備過濾概率空間(Ω，F，P)獲得，其中Ω是狀態空間，F是可測事件的σ－代數，P是概率測度，完備過濾結構{Ftt∈［0，τ］}由n≥1個初始值為0的獨立標準布朗運動Wi(t)，1≤i≤n生成.

1.1 風險中性的單因素HJM模型

令r(t)表示t時刻當期的瞬時遠期利率，對所有的t∈［0，τ］，有r(t)=f(t，t).

對每一個T≤τ，HJM(1992)利用代表遠期利率運動的隨機過程族描述了利率期限結構的動態，遠期利率動態的積分形式為:

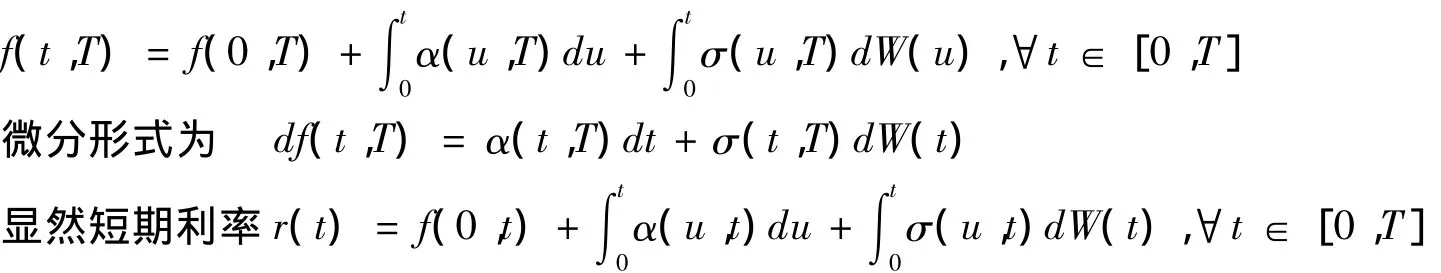
這里α:［0，t］×Ω→R是瞬時漂移率，σ:［0，t］×Ω→Rn是到期日為T的遠期利率在時刻t時的

瞬時波動率.W是一個n維標準布朗運動，過程……