多元均值方差比值檢驗

錢有程

(吉林化工學院理學院，吉林吉林132022)

變異系數(shù)(CV)是隨機變量的標準差和均值的比例，它給出了一個相對變化的度量.另一方面，夏普比例(SR)是超額預期收益與它的標準差的比例，給出了一個相對超額收益的量度.即使變量的均值和方差不相同，我們同樣可以獲得它的相對變化或者相對超額預期收益.本文在已有的二元均值方差比檢驗的基礎(chǔ)上提出了多元假設(shè)檢驗，以便可以比較多元資產(chǎn)的均值方差比，從而確定更有的投資組合［1］.

1 多元均值方差比假設(shè)檢驗

1.1 Bonferroni檢驗

著名的Bonferroni不等式:

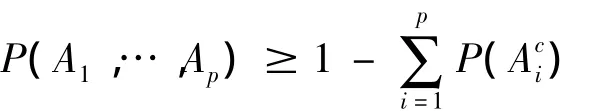
其中Ai是一事件，是它的余集.令Ai為事件 ti≤tδ/2(n)，i=1，…，p，，Bonferroni不等式變?yōu)?

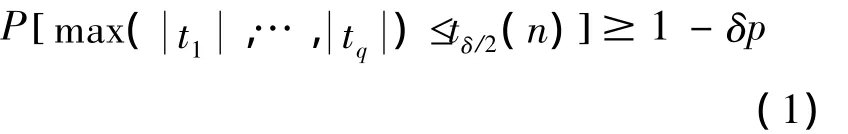
換言之，點(t1，…，tp)落在立方體中的概率是≥1 － δp.當顯著水平δ是α/p時，概率是1 － α［2］.

Bonferroni檢驗來自精確的檢驗利用Bonferroni不等式的臨界值B替換精確臨界值M.對H的正常α水平Bonferroni導出檢驗的接受域是:

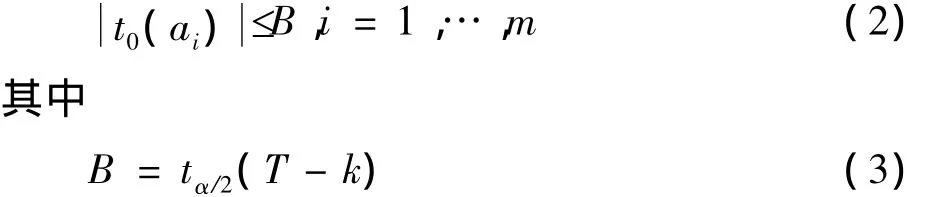
單獨假設(shè)的顯著水平是δ=α/m并且Bonferroni檢驗的顯著水平≤α.Bonferroni檢驗由利用接受域(2)的單獨假設(shè)構(gòu)成，其中臨界值B由(3)給出.z1，…，zq空間的 Bonferroni檢驗的接受域稱為Bonferroni多面體，并且t0(a1)，…，t0(am)稱為 Bonferroni方塊［3］.

1.2 多元均值方差比值檢驗

對于多元值方差比值假設(shè)我們有如下推論和證明:

推論:令 Xim，(i=1，2，…，k;m=1，2，…，n)為獨立的隨機變量，且對應的分布為N ( μi，σ2i)，在α水平下，存在k－1個導出的單獨假設(shè)

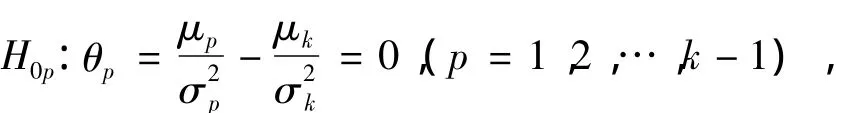
且每個單獨假設(shè)滿足臨界函數(shù)

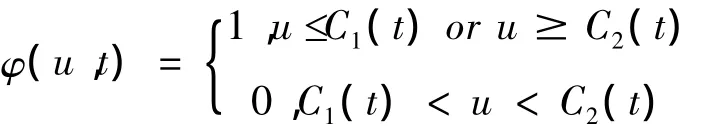
其中C1和C2滿足

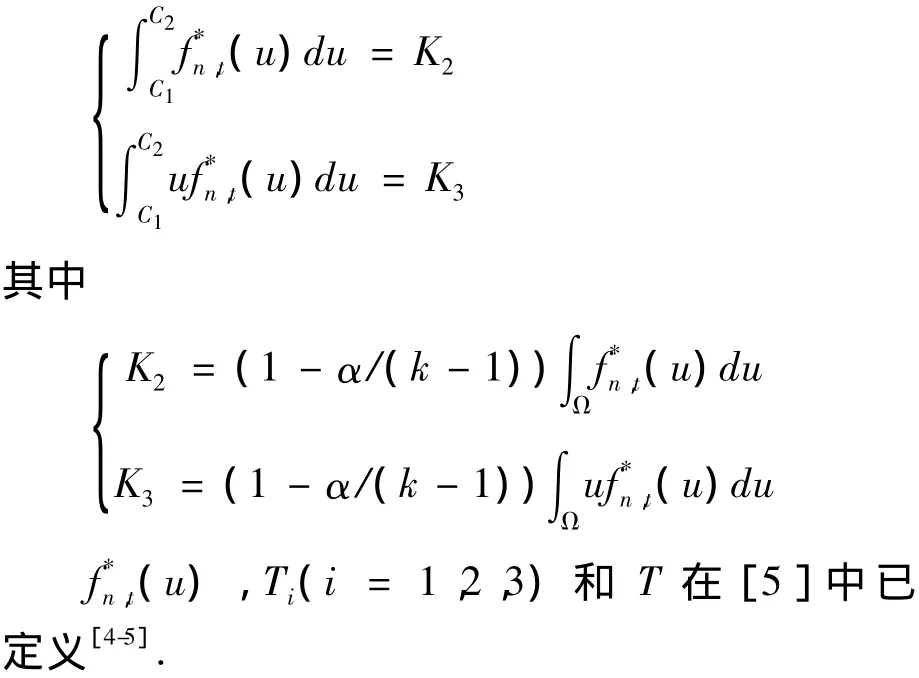
證明:利用Bonferroni檢驗，對于假設(shè)，可以導出k－1個單獨假設(shè):

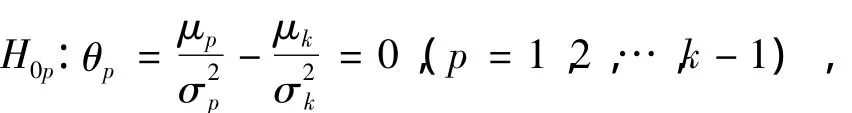
當接受 H0時，當且僅當 H0p，(p=1，2，…，k－1)均成立.對于每個單獨假設(shè)，利用Bonferroni不等式的思想:

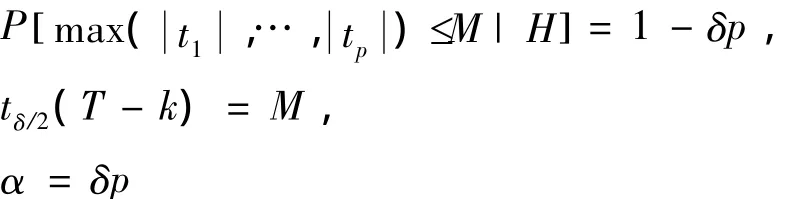
在α水平下，對于k－1個單獨假設(shè)的顯著水平是α/( k －1)，且每個單獨假設(shè)利用Lehmann(1986)的多參數(shù)……