考慮不同維修效果的多狀態(tài)可修系統(tǒng)可靠性模型

狄鵬，黎放，陳童

(海軍工程大學 管理工程系，湖北 武漢430033)

0 引言

隨著軍事裝備功能與結(jié)構(gòu)的日益復雜，系統(tǒng)功能與故障模式表現(xiàn)出多樣性的特點，將系統(tǒng)狀態(tài)簡單分為“運行”和“故障”的傳統(tǒng)可靠性分析方法已經(jīng)顯現(xiàn)出很大的局限性［1-2］。因此，多狀態(tài)系統(tǒng)于20世紀70年代被提出［3］，到20世紀80年代初步建立了多狀態(tài)系統(tǒng)的可靠性理論。

多狀態(tài)系統(tǒng)可靠性解析模型研究作為一個重要方向，受到國內(nèi)外學者的廣泛關注［4］。如Amico 等［5］利用非齊次半馬爾可夫過程研究了具有M+1 個工作狀態(tài)的系統(tǒng)可靠性問題。Lisnianski 等［6］利用多狀態(tài)馬爾可夫模型研究了具有多性能狀態(tài)的大型發(fā)電機組的可靠性規(guī)律，其中假設系統(tǒng)工作狀態(tài)的轉(zhuǎn)移服從指數(shù)分布，采用參數(shù)估計法獲取各轉(zhuǎn)移速率。Levitin 等［7］利用通用函數(shù)法和可靠性框圖研究了多狀態(tài)串并聯(lián)系統(tǒng)的可靠性規(guī)律。Moghaddass等［8］采用參數(shù)估計法對具有連續(xù)狀態(tài)劣化情況的環(huán)境監(jiān)測設備的可靠性規(guī)律進行了研究。王麗花等［9］利用馬爾可夫過程研究了離散狀態(tài)退化系統(tǒng)的可靠性問題，維修策略選擇小修和一般型更換，部件更換時間服從一般分布。Yuan 等［10］利用幾何過程研究了存在性能退化的可修系統(tǒng)可靠性問題，模型假設系統(tǒng)有一個多重休假模式的維修工，系統(tǒng)故障時間和維修工休假時間服從指數(shù)分布，維修時間為一般分布。

上述研究具有如下特點:解析建模過程復雜，模型假設條件嚴格，模型只適用于特定對象，重用性不佳。為了改善這種情況，Phase-type(PH)分布被引入到多狀態(tài)可修系統(tǒng)可靠性解析建模工作中。Frostig 等［11］研究了具有連續(xù)劣化和隨機沖擊的可修系統(tǒng)，沖擊烈度服從PH 分布。Ruiz-Castro 等［12］研究了具有多狀態(tài)部件的n 中取k 系統(tǒng)，部件壽命和維修時間均服從離散PH 分布。Segovia 等［13］研究了具有外部沖擊和內(nèi)部磨損的多狀態(tài)系統(tǒng)可靠性，沖擊到達間隔時間和沖擊損壞效果均服從連續(xù)PH 分布。

PH 分布作為指數(shù)分布的矩陣形式推廣，保持了指數(shù)分布的易處理性，其密度函數(shù)、拉普拉斯變換和各階矩等都具有簡潔的矩陣表示和概率意義。而由PH 分布在非負實數(shù)軸上全體概率分布函數(shù)中的稠密性所決定，對于任何非負隨機變量，總可以找到一個PH 分布把該隨機變量逼近到任意需要的精度。即對于未知分布規(guī)律，假設為PH 分布是合理的。因此采用PH 分布作為解析模型假設條件能夠有效提升模型的描述能力。此外，PH 分布在很多情況下使模型分析中復雜的數(shù)值積分轉(zhuǎn)化為矩陣運算，有利于提升模型的可計算性［14］。

本文對多狀態(tài)可修系統(tǒng)的一類常見現(xiàn)象展開研究，即這類系統(tǒng)通常可以根據(jù)實際需要選擇不同方式的維修，維修效果也隨之不同。本文考慮修理后恢復到修前狀態(tài)、維修效果較差和維修效果好3 種效果，假設系統(tǒng)狀態(tài)可以劃分為完好、一般和故障3 種狀態(tài)集，其中系統(tǒng)在完好和一般狀態(tài)的停留時間為系統(tǒng)工作時間。模型假設系統(tǒng)工作時間和維修時間均服從連續(xù)PH 分布，通過建立系統(tǒng)狀態(tài)馬爾可夫轉(zhuǎn)換的無窮小生成元矩陣，求得各狀態(tài)的穩(wěn)態(tài)概率向量，給出系統(tǒng)穩(wěn)態(tài)可用度、穩(wěn)態(tài)故障率的解析表達式，并通過算例驗證模型的有效性和適用性。

下面首先對連續(xù)PH 分布作簡要介紹。

1 連續(xù)PH 分布

定義［15］［0，+∞)上的概率分布函數(shù)F(·)稱為PH 分布，并具有m 階(α，T)表示，當且僅當它是一個有限狀態(tài)馬爾可夫過程的吸收時間分布，有分布函數(shù)F(x)=1 -αexp (Tx)eT.

該馬爾可夫過程具有狀態(tài)集{1，…，m，m +1}，狀態(tài)1，…，m 都是非常返的(瞬態(tài))，狀態(tài)m +1 是吸收態(tài)。初始概率為(α，αm+1)，其中α=(α1，…，αm)且滿足αeT+αm+1=1，e 為元素值均為1 的行向量，eT為e 的轉(zhuǎn)置。該馬爾可夫過程無窮小生成元Q 可寫成下列分塊形式:式中:T =(Tij)為m 階方陣，Tij≥0 (i≠j;i、j =1，…，m)表示從瞬態(tài)i 至瞬態(tài)j 的轉(zhuǎn)移率，且滿足Tii＜0;T0=(T01，…，T0m)T是非負列向量，其中T0i 表示從瞬態(tài)i至吸收態(tài)的轉(zhuǎn)移率，滿足TeT+T0=0. PH 分布中的每一個瞬態(tài)稱為相位。

2 問題描述

某多狀態(tài)系統(tǒng)的狀態(tài)集為S={1，…，n，n+1}.根據(jù)系統(tǒng)工況，可以將S 分為3 類:完好狀態(tài)，即系統(tǒng)性能保持在設計指標附近，有狀態(tài)集G ={1，…，k};一般狀態(tài)，即系統(tǒng)可以正常運行，但性能較差，有狀態(tài)集B={k +1，…，n};故障狀態(tài)，指系統(tǒng)發(fā)生停機故障，有狀態(tài)集F ={n +1}，此時必須經(jīng)過修理，系統(tǒng)才能恢復到狀態(tài)集G 或B.

由于使用和環(huán)境等因素影響，系統(tǒng)會從完好和一般狀態(tài)直接進入故障狀態(tài)。而本文考慮3 種維修效果:

1)修后恢復修前狀態(tài)，即系統(tǒng)經(jīng)過維修后，返回到發(fā)生故障前一刻的狀態(tài)，如圖1所示。

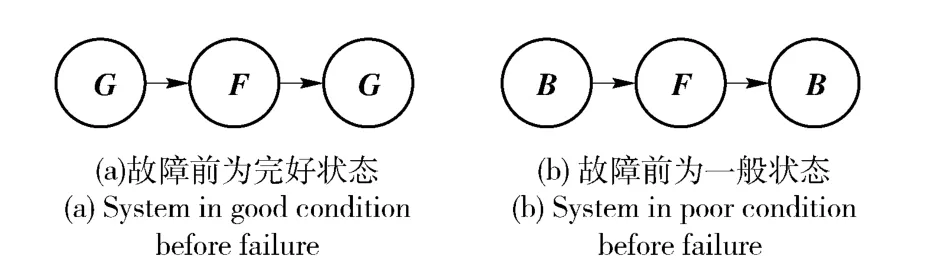
圖1 修后恢復修前狀態(tài)示意圖Fig.1 System state being the same as good/old after repair

2)維修效果較差，即系統(tǒng)經(jīng)過維修，只能恢復到一般狀態(tài)集B，如圖2所示。

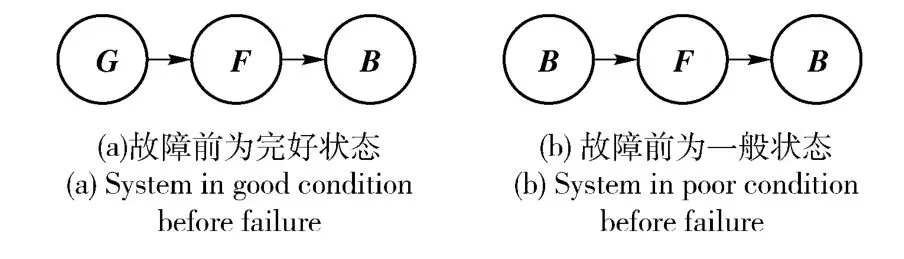
圖2 維修效果較差的系統(tǒng)狀態(tài)變化示意圖Fig.2 Transition of system state for imperfect repair

3)維修效果好，即系統(tǒng)經(jīng)過維修，恢復到完好狀態(tài)集G，如圖3所示。

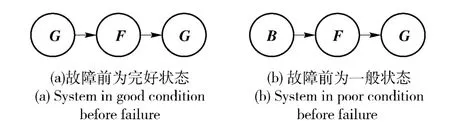
圖3 維修效果好的系統(tǒng)狀態(tài)變化示意圖Fig.3 Transition of system state for perfect repair

對該系統(tǒng)做進一步假設:

1)系統(tǒng)工作時間，即系統(tǒng)在狀態(tài)集G 和B 的停留時間服從PH 分布，(α，T)為該PH 分布的n 階不可約表示，其中α 和T 可以表示為分塊形式:α=

矩陣TGG、TGB、TBG和TBB分別表示系統(tǒng)在狀態(tài)集G 和B 內(nèi)部和相互之間的轉(zhuǎn)移速率。通常不經(jīng)過維修時，系統(tǒng)不能從一般狀態(tài)轉(zhuǎn)換到完好狀態(tài)，故TBG=0.

工作時間吸收速率矩陣T0亦可寫為分塊形式:

2)系統(tǒng)維修時間，即系統(tǒng)在狀態(tài)集F 的停留時間服從PH 分布，(β，S)為該PH 分布的m 階不可約表示。

因此，有PGGe+PGBe=e，PBGe+PBBe=e.

3 模型分析

3.1 無窮小生成元矩陣

根據(jù)系統(tǒng)狀態(tài)變化情況，需定義4 個宏狀態(tài):OG、OB、RG、RB. 系統(tǒng)狀態(tài)空間為Ω=OG∪OB∪RG∪RB，其中:OG={(i)，i∈G}表示系統(tǒng)處于完好狀態(tài)的相位i;OB={(i)，i∈B}表示系統(tǒng)處于一般狀態(tài)的相位i;RG={(i，j)，i∈G，j=1，…，m}表示系統(tǒng)故障前處于完好狀態(tài)的相位i，維修狀態(tài)處于相位j;RB={(i，j)，i∈B，j=1，…，m}表示系統(tǒng)故障前處于一般狀態(tài)的相位i，維修狀態(tài)處于相位j.

因此，該馬爾可夫鏈的無窮小生成元矩陣可以表示為

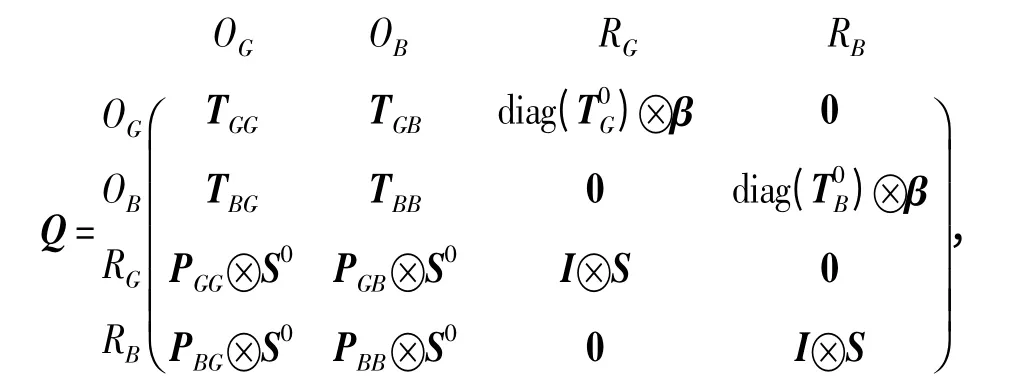
式中運算符?為Kronecker 積［14］，下面分別從4 個方面說明Q 中各元素的構(gòu)成。

3.1.1 宏狀態(tài)OX向OY(X，Y∈{G，B})的轉(zhuǎn)移

以宏狀態(tài)OG向OG的轉(zhuǎn)移為例，系統(tǒng)在OG內(nèi)部進行轉(zhuǎn)移，因此相位i(i∈G)之間的轉(zhuǎn)移率矩陣為TGG. 同理，可知宏狀態(tài)OB內(nèi)部，以及宏狀態(tài)OG和OB之間的轉(zhuǎn)移率矩陣。

3.1.2 宏狀態(tài)OX向RY(X，Y∈{G，B})的轉(zhuǎn)移

以宏狀態(tài)OG向RG的轉(zhuǎn)移為例，說明系統(tǒng)進入故障狀態(tài)的前一刻處于G，并以初始概率β 進入維修相位，因此有diag(T0G)?β，其中diag(T0G)為將單位矩陣的對角線元素換為T0G各分量。同理，可得OB向RB的轉(zhuǎn)移率矩陣。

以宏狀態(tài)OB向RG的轉(zhuǎn)移為例，因為系統(tǒng)進入故障狀態(tài)的前一刻處于B，不可能進入宏狀態(tài)RG，因此為0 矩陣。同理，可得OG向RB的轉(zhuǎn)移率矩陣。

3.1.3 宏狀態(tài)RX向OY(X，Y∈{G，B})的轉(zhuǎn)移

以宏狀態(tài)RG向OG的轉(zhuǎn)移為例，說明維修活動進入了吸收態(tài)，同時以概率矩陣PGG返回G，因此有PGG?S0. 同理，可得RG向OB、RB向OG、RB向OB的轉(zhuǎn)移率矩陣。

3.1.4 宏狀態(tài)RX向RY(X，Y∈{G，B})的轉(zhuǎn)移

以宏狀態(tài)RG向RG的轉(zhuǎn)移為例，系統(tǒng)在維修狀態(tài)內(nèi)部發(fā)生相位轉(zhuǎn)移，即I?S. 同理，可得RB向RB的轉(zhuǎn)移率矩陣。

因為不可能發(fā)生RG向RB、RB向RG的轉(zhuǎn)移，故相應的轉(zhuǎn)移矩陣均為0 矩陣。

3.2 穩(wěn)態(tài)概率向量

當系統(tǒng)進入穩(wěn)態(tài)時，由連續(xù)時間馬爾可夫過程穩(wěn)態(tài)概率向量定義［15］，無窮小生成元Q 矩陣中各個宏狀態(tài)所對應的概率組成了穩(wěn)態(tài)概率向量π=(πOG，πOB，πR，πRB)，并且π 滿足如下方程組:

將上述方程組展開，得(2)式～(6)式:

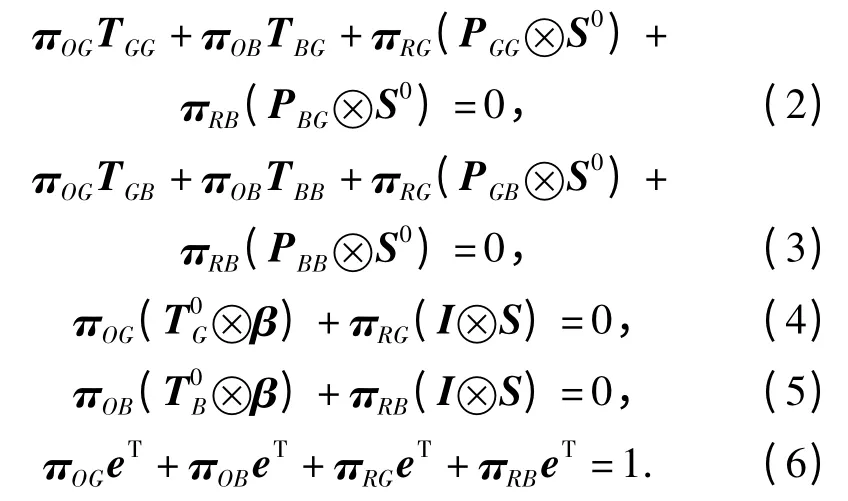
由(4)式和(5)式可知:

將(7)式、(8)式代入(2)式、(3)式和(6)式，即可求得π.

3.3 系統(tǒng)特性

3.3.1 系統(tǒng)穩(wěn)態(tài)可用度

在獲得π 后，可以確定系統(tǒng)穩(wěn)態(tài)可用度，即系統(tǒng)處于宏狀態(tài)OG和OB的概率:

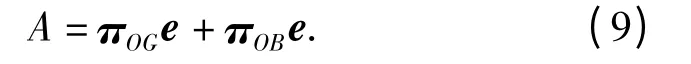
3.3.2 系統(tǒng)穩(wěn)態(tài)故障率

故障率是系統(tǒng)分別從完好和一般狀態(tài)進入維修狀態(tài)的速率，當系統(tǒng)進入穩(wěn)態(tài)后，穩(wěn)態(tài)故障率為

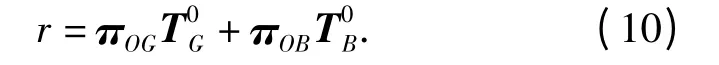
3.4 維修效果對系統(tǒng)的影響

下面考慮模型的特例:系統(tǒng)只存在一種維修效果的情況。

3.4.1 修后恢復修前狀態(tài)

令向量δG為從維修狀態(tài)進入完好狀態(tài)各相位的概率，向量δB為從維修狀態(tài)進入一般狀態(tài)各相位的概率。則PGG=eδG，PGB=0，PBG=0，PBB=eδB，并有

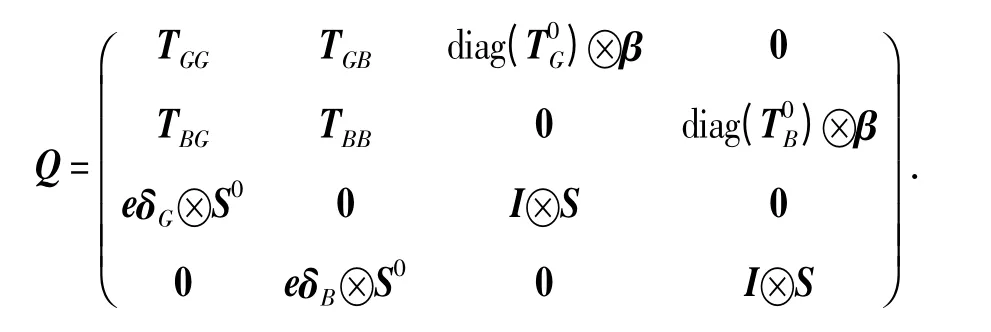
3.4.2 維修效果較差

此時PGG=0，PGB=eδB，PBG=0，PBB=eδB，并有

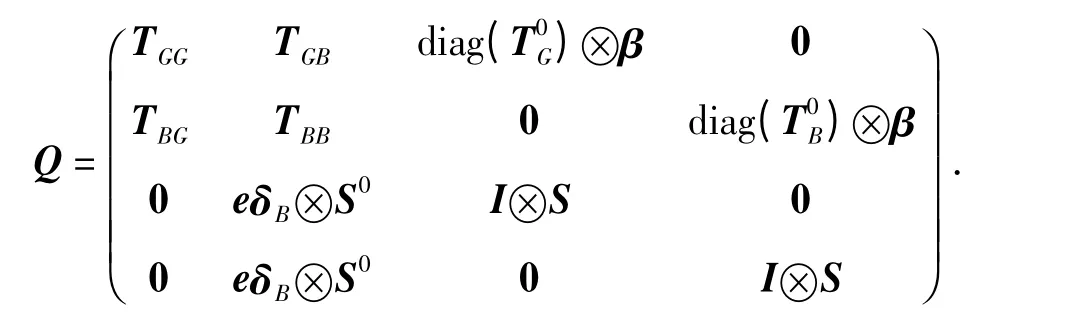
3.4.3 維修效果好

此時PGG=eδG，PGB=0，PBG=eδG，PBB=0，并有

4 算例

4.1 模型有效性驗證

某型艦用電站系統(tǒng)具有5 種工作狀態(tài)，如表1所示。

表1 電站系統(tǒng)工作狀態(tài)表Tab.1 Operating states of power station

將該型電站系統(tǒng)功率在50%以上的工況劃分為完好狀態(tài)，其余工況歸為一般狀態(tài)，故障停機時為故障狀態(tài)。該系統(tǒng)初始狀態(tài)概率向量為α=(1，0，0，0，0)。對該型電站系統(tǒng)長期的運行和維修記錄等數(shù)據(jù)進行分析，可得各工況之間的狀態(tài)轉(zhuǎn)移率矩陣為

維修時間分布為

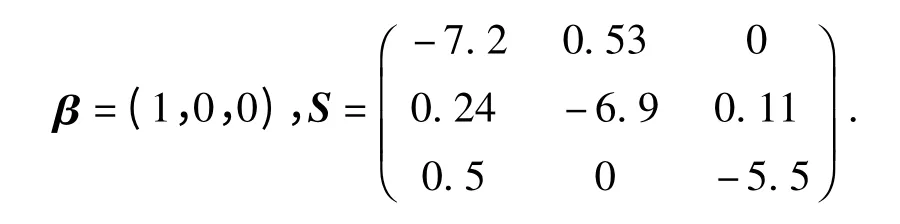
系統(tǒng)維修后狀態(tài)轉(zhuǎn)移概率矩陣為

由3.2 節(jié)得出系統(tǒng)穩(wěn)態(tài)概率向量后，根據(jù)(9)式和(10)式，可得系統(tǒng)穩(wěn)態(tài)可用度A =0.961 6，系統(tǒng)穩(wěn)態(tài)故障率r=0.255 7 次/1 000 h.

該算例說明利用本文模型能夠有效獲得該類多狀態(tài)可修系統(tǒng)的可靠性參數(shù)。下面通過改變模型輸入的隨機分布類型，驗證模型的適用性。

4.2 模型適用性驗證

當系統(tǒng)維修時間服從指數(shù)分布、Weibull 分布等典型分布時，可以將這些分布表示為PH 形式［16］，再利用本文模型即可求得系統(tǒng)可靠性。首先假設系統(tǒng)維修時間服從修復率為μ 的指數(shù)分布，則β =(1)，S=(-μ). 令μ 在區(qū)間(0，20］中變化，可以計算得到修復率分別與系統(tǒng)穩(wěn)態(tài)可用度、系統(tǒng)穩(wěn)態(tài)故障率之間的關系，如圖4和圖5所示。

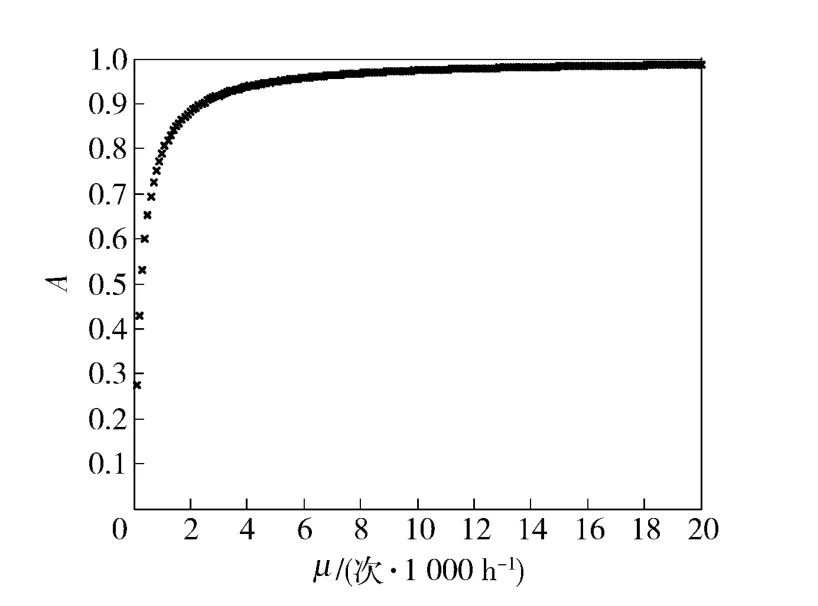
圖4 修復率與系統(tǒng)穩(wěn)態(tài)可用度關系圖Fig.4 Relationship between repair rate and stationary availability

圖5 修復率與系統(tǒng)穩(wěn)態(tài)故障率關系圖Fig.5 Relationship between repair rate and stationary failure rate

圖4說明修復率取值的增大能夠有效增加系統(tǒng)穩(wěn)態(tài)可用度。對于本文研究的多狀態(tài)可修系統(tǒng)，在系統(tǒng)進入穩(wěn)態(tài)之前，其故障率并非常數(shù)，只有當系統(tǒng)進入穩(wěn)態(tài)后，在給定修復率下，系統(tǒng)的穩(wěn)態(tài)故障率才會固定。而隨著修復率取值的增大，系統(tǒng)穩(wěn)態(tài)故障率也逐步上升，并最終趨于穩(wěn)定，如圖5所示。這是因為修復率直接影響到系統(tǒng)在完好狀態(tài)和一般狀態(tài)的停留時間，即穩(wěn)態(tài)概率πOG和πOB隨著修復率取值的增大而增大，結(jié)合(10)式可知，r 也將增大。圖5正是反映了r 與μ 之間的這種正相關關系。而r 最終趨向于某一穩(wěn)定值，這正是在忽略維修時間情況下系統(tǒng)長期運行時，系統(tǒng)固有的故障率。

當維修時間為Weibull 分布時，令a 為形狀參數(shù)，b 為尺度參數(shù)。采用文獻［16］方法將各Weibull分布擬合為PH 分布形式，然后帶入本文模型可得對應系統(tǒng)可靠性參數(shù)如表2所示。

從表2可以看到，當給定形狀參數(shù)a 后，尺度參數(shù)b 與系統(tǒng)穩(wěn)態(tài)可用度A 和系統(tǒng)穩(wěn)態(tài)故障率r 均表現(xiàn)出正相關關系，分別如圖6和圖7所示，可以清楚地看到:b 取不同的值時，a 對A、r 的影響機理并不會因為b 值不同而發(fā)生改變，顯現(xiàn)出本文算法的穩(wěn)定性。

算例說明本文模型能夠方便地用于不同隨機分布類型的輸入，適用范圍有所拓展。

表2 維修時間服從Weibull 分布時的系統(tǒng)可靠性Tab.2 System reliability measures with Weibull repair time

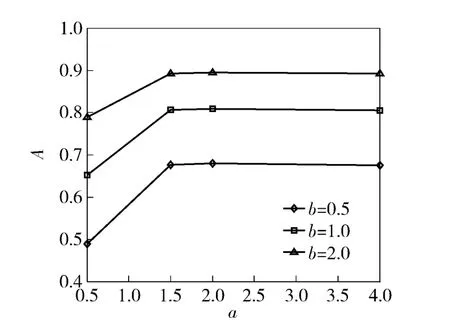
圖6 形狀參數(shù)a 對系統(tǒng)穩(wěn)態(tài)可用度的影響Fig.6 Influence of shape parameter a on system stationary availability

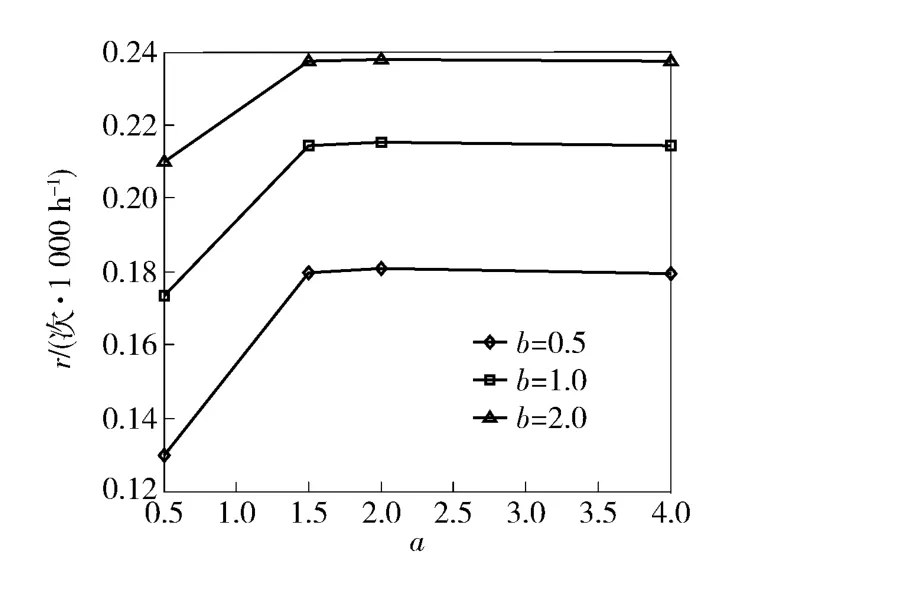
圖7 形狀參數(shù)a 對系統(tǒng)穩(wěn)態(tài)故障率的影響Fig.7 Influence of shape parameter a on system stationary failure rate

5 結(jié)束語

本文采用PH 分布研究了具有不同維修效果的多狀態(tài)可修系統(tǒng)可靠性規(guī)律，在保證良好解析特性的同時，有效提升了模型的描述能力。本文模型在計算時主要涉及矩陣運算，而目前高性能計算機和矩陣解析理論的應用能對大型矩陣的運算提供良好的支持，算例充分演示了模型的良好計算性和適用性。

References)

［1］ Zio E. Reliability engineering:old problems and new challenges［J］. Reliability Engineering and System Safety，2009，94:125 -141.

［2］ Ying K G，Jing L. Multi-state system reliability:a new and systematic review［J］. Procedia Engineering，2011，29:531 -536.

［3］ Barlow R E，Wu A S. Coherent systems with multi-state components［J］，Mathematics of Operations Research，1978，3:275 -281.

［4］ Lisnianski A，F(xiàn)renkel I，Ding Y. Multi-state system reliability analysis and optimization for engineers and industrial managers［M］，London:Springer，2010:8 -19.

［5］ Amico G D，Biase G D，Manca R. A customer’s utility measure based on the reliabilityof multi-state systems［J］. Decisions in Economics Finance，2011，34(1):1 -20.

［6］ Lisnianski A，Elmakias D，Laredo D，et al. A multi-state Markov model for a short-term reliability analysis of a power generatingunit［J］. Reliability Engineering and System Safety，2012，98(1):1 -6.

［7］ Levitin G，Xing L. Reliability and performance of multi-state systems with propagated failure shaving selective effect［J］. Reliability Engineering and System Safety，2010，95:655 -661.

［8］ Moghaddass R，Zuo M. A parameter estimation method for a condition-monitored device under multi-state deterioration［J］. Reliability Engineering and System Safety，2012，106:94 -103.

［9］ 王麗花，岳德權(quán)，張靜，等. 具有小修和一般型更換策略的多狀態(tài)退化系統(tǒng)［J］. 遼寧工程技術大學學報:自然科學版，2011，30(6):935 -938.WANG Li-hua，YUE De-quan，ZHANG Jing，et al. A multi-state degraded system with minimal repairs and the replacement policy in general distribution［J］. Journal of Liaoning Technical University:Natural Science，2011，30(6):935 -938.(in Chinese)

［10］ Yuan L，Xu J. A deteriorating system with its repairman having multiple vacations［J］. Applied Mathematics and Computation，2011，217(10):4980 -4989.

［11］ Frostig E，Kenzin M. Availability of inspected systems subject to shocks-a matrix algorithmic approach［J］. European Journal of Operational Research，2009，193(1):168 -183.

［12］ Ruiz-Castro J E，Li Q L. Algorithm for a general discrete k-outof-n:G system subject to several types of failure with an indefinite number of repairpersons［J］. European Journal of Operational Research，2011，211(1):97 -111.

［13］ Segovia M C，Labeau P E. Reliability of a multi-state system subject to shocks using phase-type distributions［J］. Applied Mathematical Modelling，2013，37(7):4883 -4904.

［14］ 陳童. 基于PH 分布和馬爾可夫到達過程的裝備備件需求與庫存模型研究［D］. 長沙:國防科學技術大學，2010.CHEN Tong.Research on demand and inventory models of equipment spare parts based on phase-type distribution and Markovian arrival process［D］. Changsha:National University of Defense Technology，2010.(in Chinese)

［15］ 田乃碩. 休假隨機服務系統(tǒng)［M］. 北京:北京大學出版社，2001:5 -7.TIAN Nai-shuo. Queuing systems with sever vacations［M］，Beijing:Peking University Press，2001:5 -7.(in Chinese)

［16］ 黃卓.Phase-type 分布數(shù)據(jù)擬合方法及其應用研究［D］. 長沙:國防科學技術大學，2007.HUANG Zhuo. Research on phase-type distributions data fitting method and its applications［D］. Changsha:National University of Defense Technology，2007.(in Chinese)