單通道多分量偽碼復合線性調頻信號分離及參數估計

朱航，張淑寧，趙惠昌

(1.南京理工大學 電子工程與光電技術學院，江蘇 南京210094;2.解放軍73015 部隊，浙江 湖州313000)

0 引言

由于具有頻率時變、截獲概率低等特點，非平穩信號在雷達、聲納和無線通信領域得到極大重視，作為一種特殊的非平穩信號，線性調頻(LFM)信號在雷達目標檢測、近程探測、引信抗干擾等領域得到廣泛應用。而為了獲得更好的抗干擾性能和低截獲概率，近些年來，國內外多種較為先進的雷達引信系統都采用偽碼復合線性調頻(PRBC-LFM)信號，它同時兼具了偽隨機碼和LFM 信號的特點，具有距離速度分辨率高、測速測距精度高、抗干擾性能好和截獲概率低等優點。目前已有不少文獻提出了針對PRBC-LFM 信號的參數提取方法，但多是基于合作接收機和先驗信息部分已知的假設，如文獻［1 -2］需要知道偽隨機碼序列或其功率譜，文獻［3 -4］提出的算法需要知道碼元寬度和載頻，但對于信號非合作的雷達引信信號偵察接收機，很難獲得這些先驗信息;文獻［5 -6］提出了對PRBC-LFM 信號識別和參數估計的譜相關方法，需滿足調頻帶寬大于編碼數與脈沖寬度之比，且計算量較大，文獻［7 -9］提出了基于時頻分布的偵察信號參數估計方法，但需要在時頻平面進行二維搜索，計算量也較大。雖然上述這些方法或多或少存在一些局限，但是在對單分量的PRBC-LFM 信號進行參數估計時，都能達到一定的效果。然而，在戰場環境中，由于信道資源十分寶貴，當在同一頻段同時接收到多個PRBCLFM 信號時，上述的這些方法不能夠對這種單通道多分量信號進行較好的分析。本文基于對多分量PRBC-LFM 信號的研究，提出噪聲背景下實現信號分離和參數估計的方法，較好地解決了對調制參數和偽碼進行估計的問題，實現了多分量信號的分離。

1 單通道多分量PRBC-LFM 信號

1.1 PRBC-LFM 信號

在一個重復周期Tr內，LFM 信號的相位表達式可以表示為

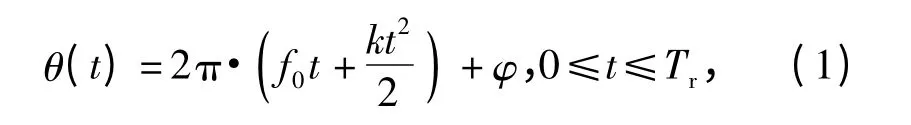
式中:f0為LFM 信號的載頻;k 為線性調頻斜率;φ是信號的初始相位。那么可以得到對該重復周期Tr內LFM 信號的描述:

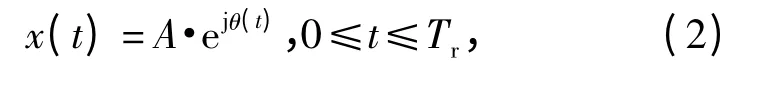
式中:A 為信號幅度，只要將這樣的信號按周期Tr重復，即可得到周期的LFM 信號。PRBC-LFM 信號可以由LFM 信號和偽隨機碼相乘得到，表示為

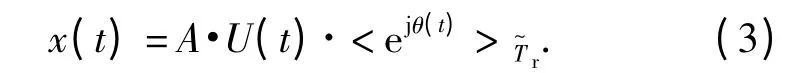
(3)式中，對于連續信號用＜·＞Tr表示變量取值范圍限定在0≤t≤Tr，＜· ＞表示在限定取值范圍為0≤t≤Tr的基礎上將信號以Tr為周期重復多次以進行延拓;相對應地，對于離散信號用＜·＞Nr表示變量取值范圍限定在1≤n≤Nr，＜·＞表示在限定取值范圍為1≤n≤Nr的基礎上將信號以Nr為周期重復多次以進行延拓。U(t)的表達式為

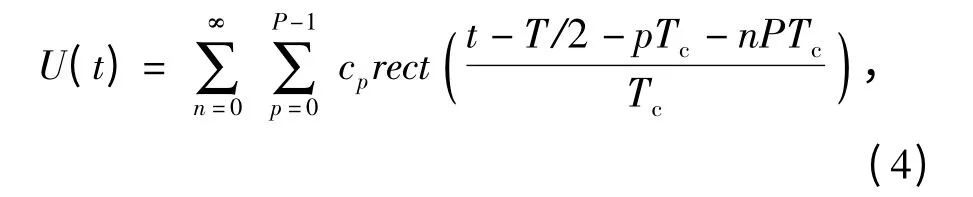
1.2 單通道多分量PRBC-LFM 信號

多分量PRBC-LFM 信號可以表示成(5)式:

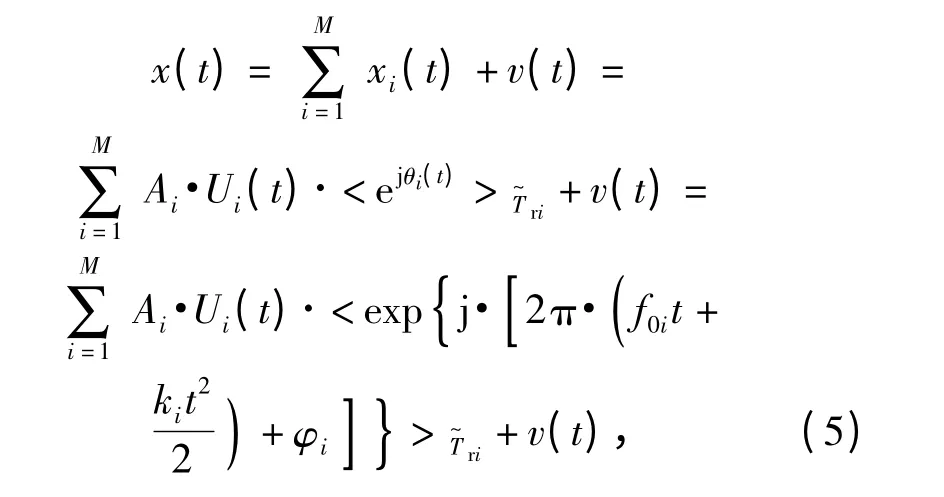
式中:M 表示為分量信號個數;v(t)表示噪聲;xi(t)表示第i 個分量的PRBC-LFM 信號。

這里所示的每個分量可以用參數(Ai，f0i，ki，φi，Tri)及對應的偽隨機碼序列Ui(t)來表示，其中Ui(t)包含了信號的偽隨機序列長度Pi和偽碼碼元寬度Tci.

2 調制參數及偽碼估計

對于各參數及偽碼的估計，都是基于信號的離散表示形式進行的，該離散表示形式(本文中，離散信號用方括號［n］表示，連續信號用圓括號(t)表示)可以表示為

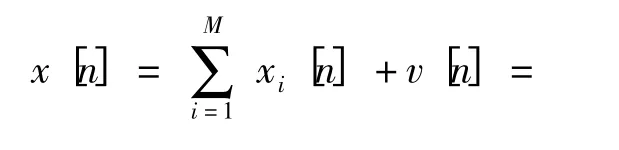
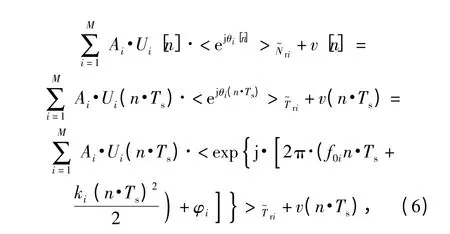
式中:Ts表示對信號的采樣周期;Nri為重復點數，與重復周期Tri相對應，有Tri=Nri·Ts.則各分量的離散形式可以用參數(Ai，f0i，ki，φi，Nri)表示。

本節中為了更好地說明參數估計方法，假設估計值同真實值無差別，而在實際情況中，估計值會存在一定誤差。

2.1 重復周期的估計

由第1 節可知，PRBC-LFM 信號都具有周期性，所以首先需要估計出各分量信號的周期。

對于(7)式所示的R 行N 列矩陣:

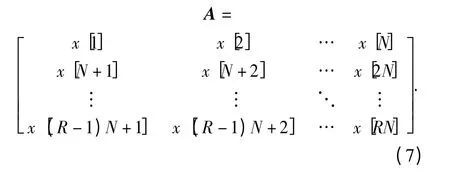
若該矩陣各行呈周期性，則該矩陣的秩為1，那么如果對A 做奇異值分解，得到的奇異值只有第一個不為0 且較大，其他奇異值均為0 或十分接近0;否則求解出多個不為0 且數值較接近的奇異值［10］.

因此，對于多分量PRBC-LFM 信號，可以按照(7)式，以1 為步進改變N 值，構建矩陣A，進行奇異值分解，對于不同的N，求解出奇異值比σ1/σ2，構建奇異值比譜。當N =N1時，如果N1為某一分量信號的重復周期，則在譜中會出現一個很明顯的峰值，而其他分量信號的周期不為N1，可以視之為噪聲，對σ1的貢獻很小，可以忽略不計。因此，可以通過找出這樣的峰值，找出分量信號的重復周期Tr1=TsN1，而且必須注意的是，若分量信號的幅度越大，則其所對應的奇異值比譜上的峰值越大，所以，應該優先找出峰值較大時所對應的分量信號重復周期。

如果通過奇異值比譜，可以估計出多個不同的周期，那么說明各分量信號重復周期不盡相同，此時的信號參數估計問題會較簡單;當只估計出一個周期時，則說明各分量信號周期相同，此時的參數估計問題相比而言要稍顯困難，具體的估計步驟在下文中給出。

2.2 取平方消除偽碼影響

由于在混合信號中，各分量是由偽隨機碼和LFM 信號復合而成，因此，原本用于提取LFM 信號的方法無法被應用。

考慮對(6)式中混合信號取平方，得到(8)式:

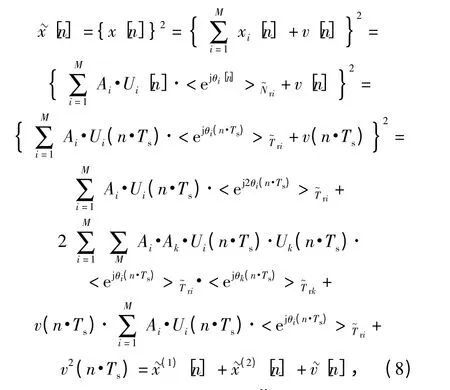
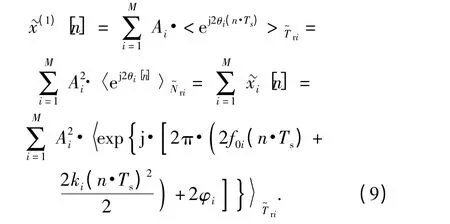
也就是說，通過取平方，消除了偽碼影響，得到了M 個新的周期LFM 信號同原分量相比，重復周期不變，它們的參數可以表示為(A2i，2fi，2ki，2φi，Tri).

2.3 周期積累減小噪聲影響

通過前面的奇異值比譜，確定了一個重復周期對應點數N1(相應的重復周期Tr1=N1Ts)后，而后又對混合信號取平方，這一步中，分別取LN1點的信號x［n］和［n］，令:

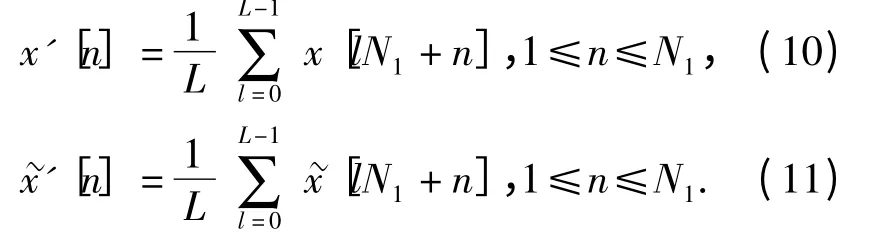
假設混合信號中有Q 個周期為N1的信號，那么經過周期積累后，對這些其余的周期不為N1的信號包括噪聲，都由于積累取平均能量減弱了，因此可以將這些信號作為新的噪聲分量，則(10)式和(11)式可以繼續寫作:

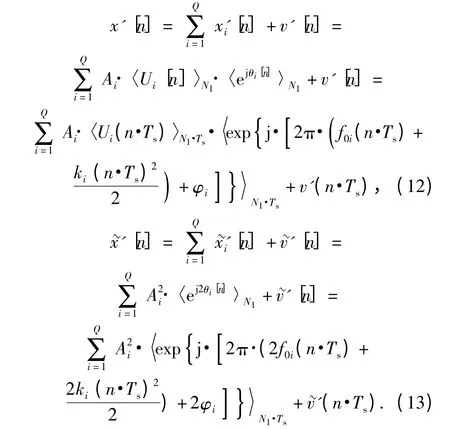
(12)式和(13)式中，由于取值范圍限定在1≤n≤N1(0≤t≤N1Ts)，所以不進行周期延拓，只用符號＜·＞N1和＜·＞N1·Ts.

2.4 調頻斜率的估計

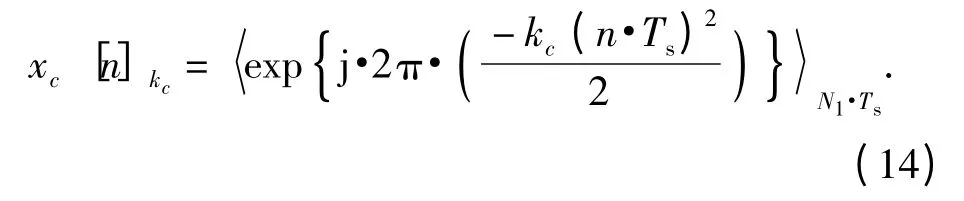
將xc［n］kc同［n］相乘，當kc=2kq時，得到:

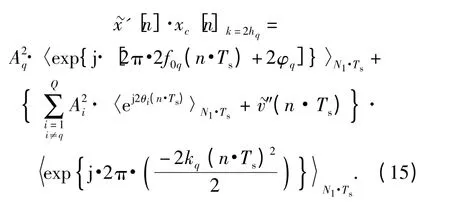
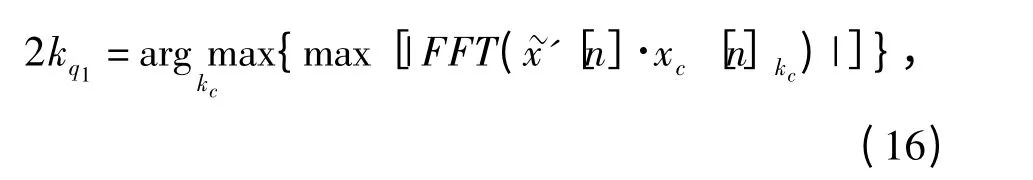
就得到了對2kq1的估計。

這里需要進一步說明的是，由于kc是以一定的步進變化的，事先不清楚2kq1的取值范圍，因此對于kc初始值和步進的設置很難明確，造成(16)式的搜索時間較長。這里，可以利用分數階傅里葉變換(FRFT)針對LFM 信號的聚斂特性［11］，先對平方處理周期積累后的混合信號［n］進行FRFT，得到其變換域上幅值最高處所對應的階數p，而后利用(17)式計算其斜率的粗略值Kr:

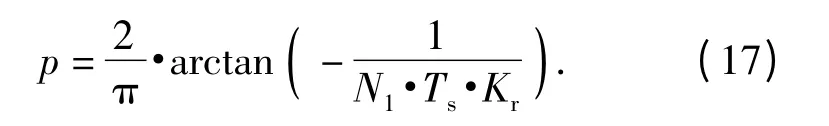
而后，使kc的取值在粗略值周圍的一個小范圍Δk內，kc∈［Kr-Δk，Kr+Δk］，以一定的步進改變kc的值，再進行(16)式計算，將減小搜索2kq1的時間。

2.5 載頻的估計

在2.4 節中，估計出2kq1之后，找出［n］·xc［n］kc=2kq1頻譜上能量最大點對應的頻率，就是對載頻2f0q1的估計，即

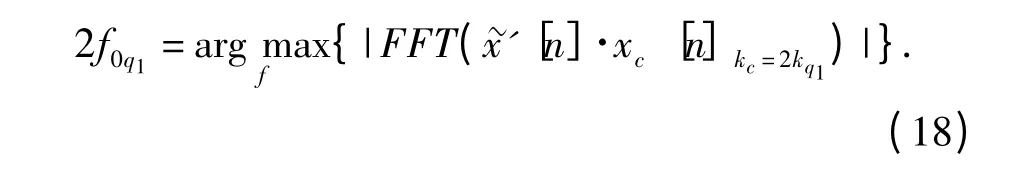
2.6 初始相位的估計

估計出(N1，2kq1，2f0q1)后，建立參考信號x'c［n］，其表達式為

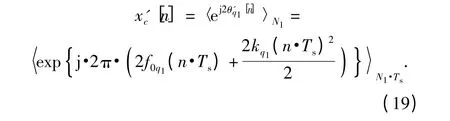
將x'c［n］的實部同［n］做內積，得到:

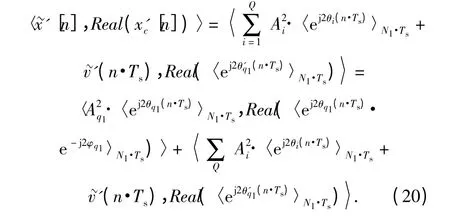
(20)式中，最后得到的兩項中，第二項中由于剩余信號同參考信號不相關，所以內積為0，因此對(20)式只考慮第一項，即

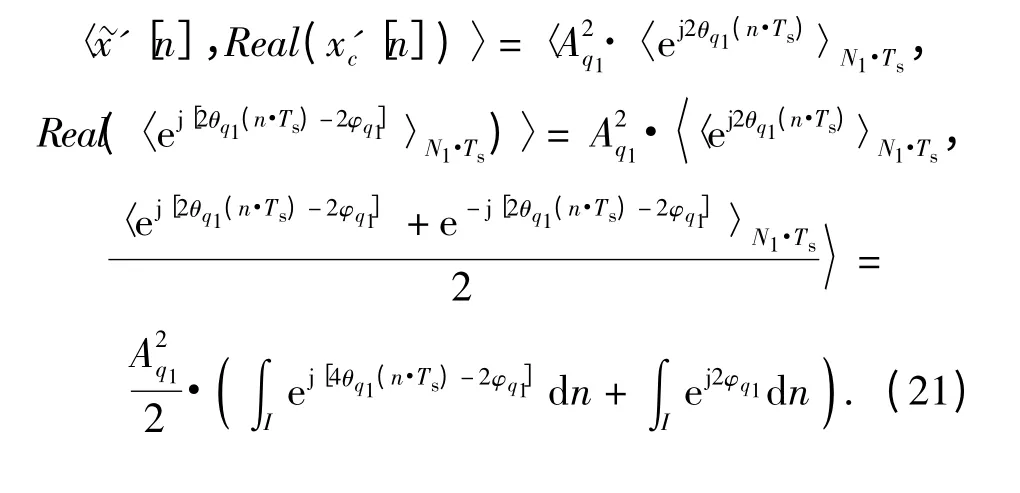
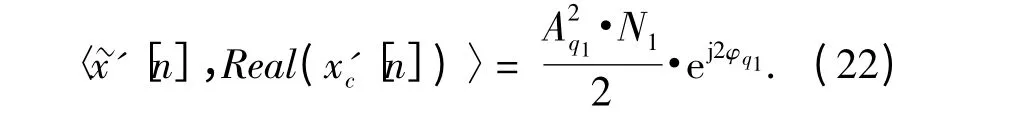
2.7 信號幅度及偽碼的估計

在求出(N1，2kq1，2f0q1，2φq1)之后，再次建立一個參考信號xd［n］，其表達式為

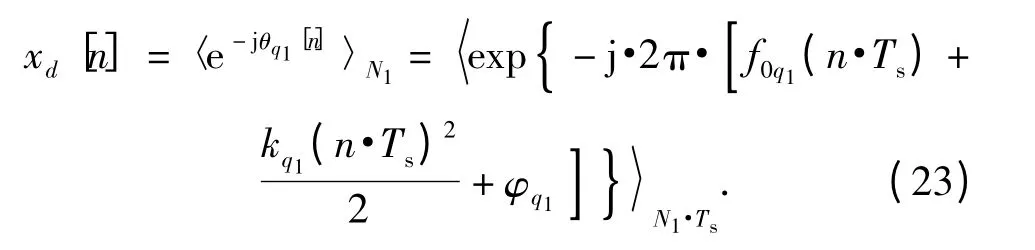
將未經平方處理的周期積累后的信號x'［n］同xd［n］相乘，得到:

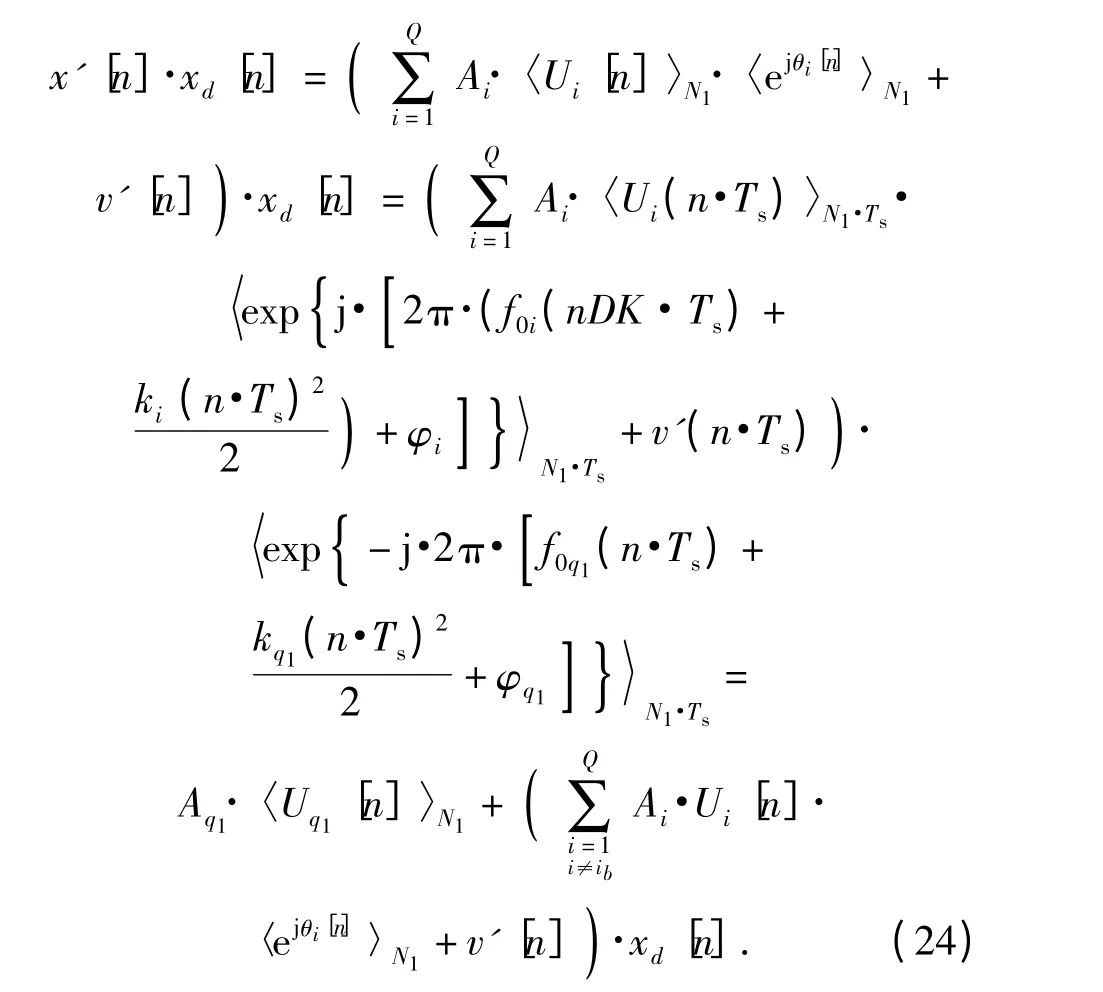
此時，(24)式得到的最后結果中，Aq1·〈Uq1［n］〉N1為實信號，它的虛部為0;而剩下的部分為復信號，有實部部分也有虛部部分。下面就是要從x'［n］·xd［n］中得到這個實信號Aq1·〈Uq1［n］〉N1.

可以知道，對信號取實部得到:

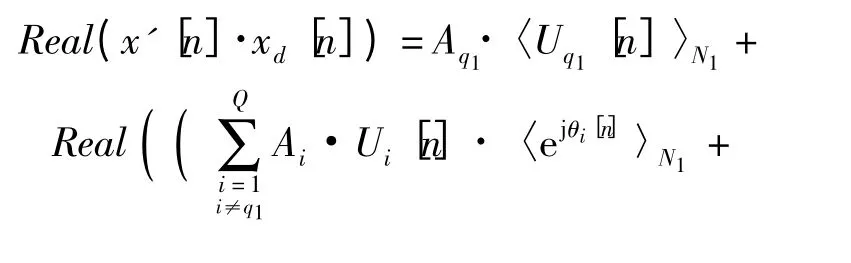
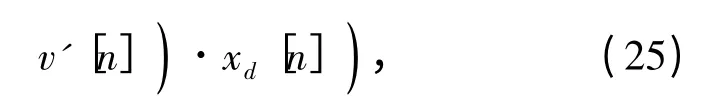
而對信號取虛部可以得到:

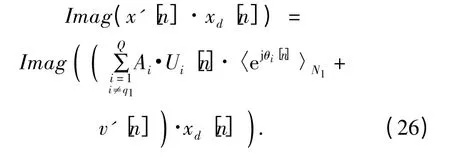
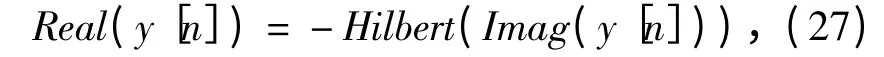
式中:Hilbert(·)表示求希爾伯特變換。將該式應用于求解Aq1·〈Uq1［n］〉N1，得到(28)式:

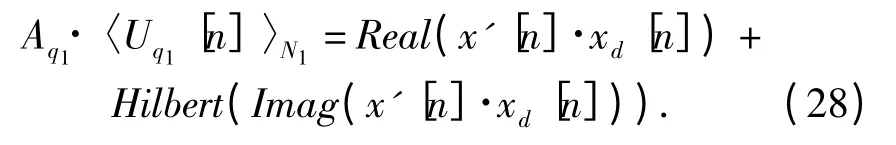
至此，就求得了一個N1周期內的Aq1·〈Uq1［n］〉N1波形，通過(29)式可以求得該分量信號的幅度，本文中假設分量信號幅度均為正數。

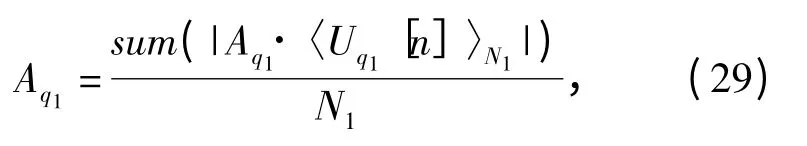
式中:sum(·)表示求所有點的加和。將Aq1·〈Uq1［n］〉N1除以Aq1就得到了理論上的一個N1周期內的偽碼波形，當然不可避免地要受到噪聲的影響，所以最后需要對波形進行整形處理，得到波形表達式:

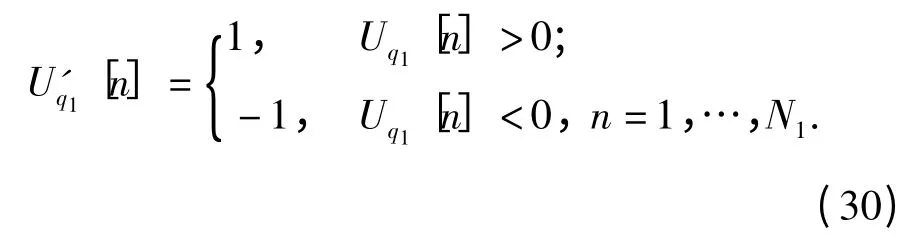
令A1=Aq1，f01=f0q1，k1=kq1，φ1=φq1，Nr1=N1和U1［n］=〈U'q1［n］〉，則重構出的第一個PRBCLFM 分量可以用參數(A1，f01，k1，φ1，Nr1)和偽碼序列U1［n］表示，該重構信號的離散形式可以表示為:

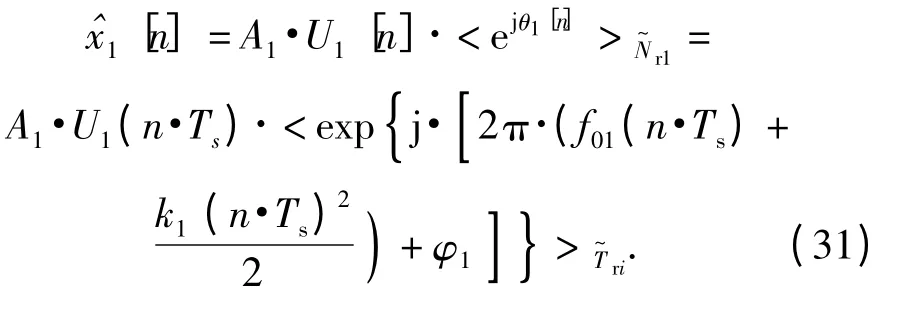
將該分量從混合信號中減去，重復本節步驟，就能依次估計出剩余各個分量信號的參數及偽碼并分離它們。

3 停止分解閾值的自適應確定

在第2 節中，給出了對多分量信號中各分量參數進行估計的方法，當估計出某一分量的各項參數及偽碼序列后，重構該分量信號，將其從混合信號中減去，重復第2 節步驟求解剩余分量。然而，對于接收到的混合信號，事先并不知道其中含有幾個分量，那么，就無法確定進行多少次分解是合適的，因此，在本節中，針對含有噪聲的多分量信號，介紹如何確定停止分解閾值的自適應方法。

對于混合信號x(n)，能夠求解出其能量SPx:

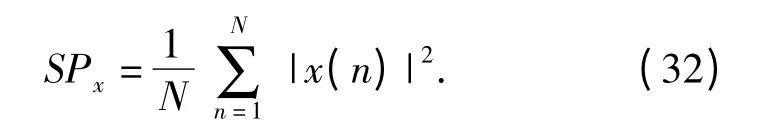
如果能夠知道混合信號的信噪比SNR，則通過求解方程組:

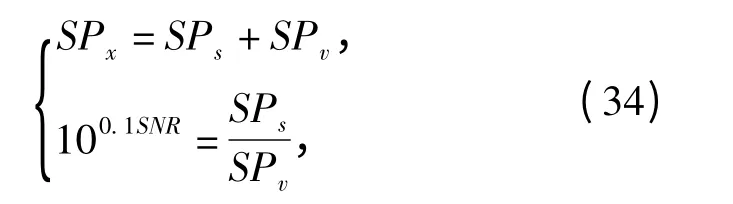
就能確定無噪信號同噪聲信號的能量值SPs和SPv，那么對于每次分解后剩余的信號能量SP(k)，k 表示分解次數，若SP(k)＜(1 +δ·100.1SNR)SPv=SPv+δ·SPs(δ 取小于1 的值，可以取0.01 ～0.20)，則可以認為對混合信號中各分量的分解已經完成，剩下的只是噪聲，這里(1 +δ·SNR)SPv即為停止分解的閾值，該閾值表示某次分解后，當混合信號中除噪聲能量以外，剩余的無噪信號能量小于最初能量的δ 倍時，可以認為剩余的無噪信號能量較小，則停止分解。

因此，需要對混合信號的SNR 進行估計。這里的信噪比估計采用自相關矩陣特征值分解法，該方法能夠適用于本文的多分量情況［12］。對混合信號構建自相關矩陣并對其做特征值分解，得到特征值bi(i=1，…，L)，且滿足:

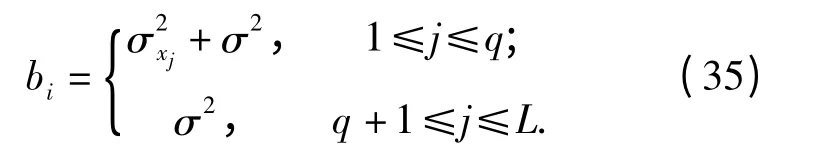
而后定義MDL 函數如(36)式所示，并求得使該函數值最小的k 值即為對q 的估計:q =

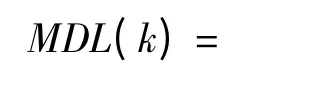
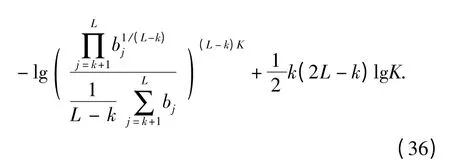
確定了q 之后，便可得到對σ2的估計如(37)式所示;進一步得到對信噪比的估計如(38)式所示:

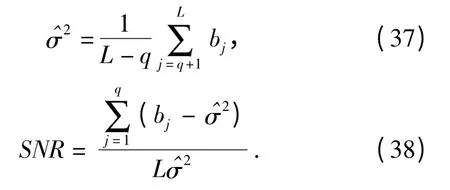
通過仿真，發現該方法對多分量信號的信噪比估計最大誤差不超過0.6 dB，平均誤差為0.132 dB，圖1為-5 dB ～25 dB 時，利用該方法對信噪比的估計同真實值之間的對比。

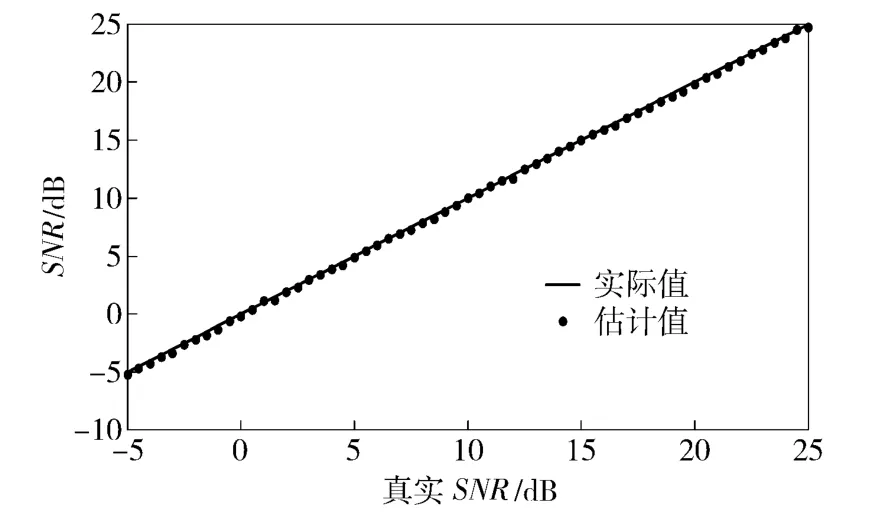
圖1 真實信噪比同估計信噪比的對比Fig.1 Contrast of true and estimated SNRs

4 仿真與分析

為說明本文方法的有效性，對含有3 個分量的多分量PRBC-LFM 信號進行分離，多分量信號處于5 dB 信噪比下。雖然在實際情況中，出現各分量信號周期相同的情況概率較小，但是為了充分驗證本方法，在這里仿真中考慮較為復雜的情況，有兩個分量信號重復周期相同。取采樣頻率為51.2 MHz 時，各個分量所對應的參數如表1所示。

各個分量所對應的偽隨機序列如圖2所示。

該多分量信號前256 個點的時頻分布繪于圖3中，圖3(a)是含噪情況下的，圖3(b)為理想情況及無噪情況下的。從圖3中可以看出，多分量PRBCLFM 信號在時域及頻域上均重疊且在時頻面上彼此交織在一起，現有的一般時頻分析法無法對這種多分量信號進行分析，這是很難實現信號分離的多分量信號混合形式，在噪聲條件下，困難更大。

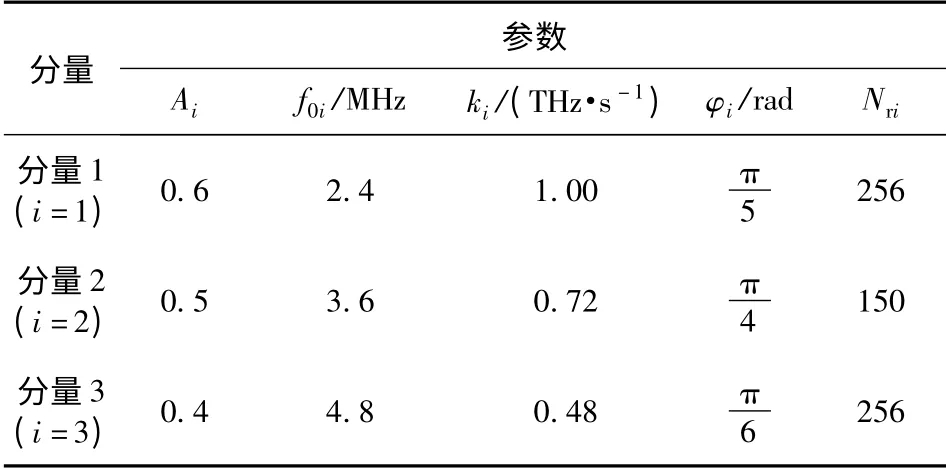
表1 多分量PRBC-LFM 信號各參數Tab.1 The parameters of multi-component signal

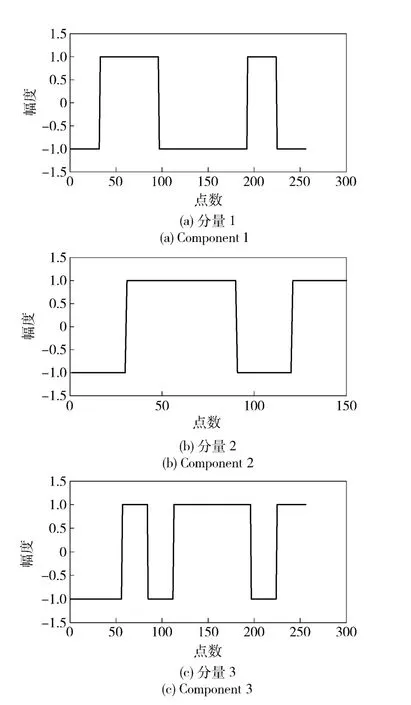
圖2 各分量對應的偽隨機序列波形Fig.2 The pseudo random sequence of each component

首先，按照第3 節所述方法，得到估計的信噪比為SNR=5.041 1 dB，并計算得到混合信號能量為1.201 4.而后，建立方程(39)式:

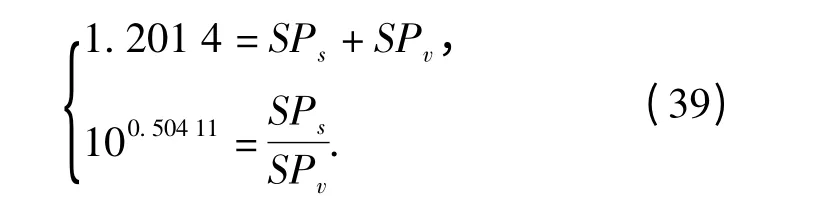
得出SPv=0.286 6，當δ =0.1 時，閾值(1 +δ·100.1SNR)SPv=0.378 1.

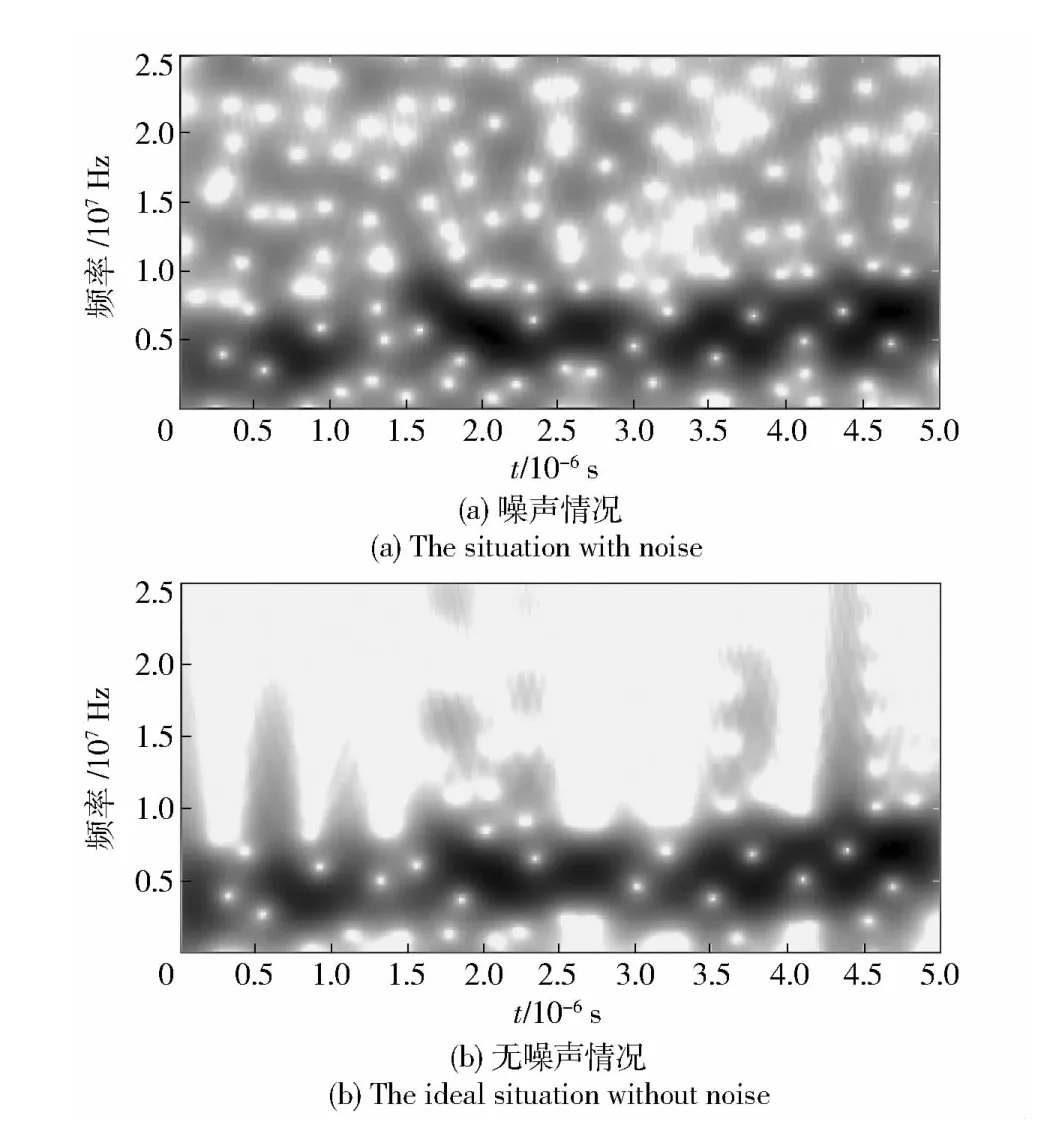
圖3 時頻分布Fig.3 The time-frequency distribution

得出閾值之后，按照第2 節所給方法，逐一估計各信號參數。

4.1 估計信號周期

以2.1 節方法，構建奇異值比譜，在譜圖中發現最大峰值對應點為256，因此令256 為第一個待分離信號的周期點數，該奇異值比譜如圖4所示。求出重復周期點數后，可以進行平方處理和周期積累處理。

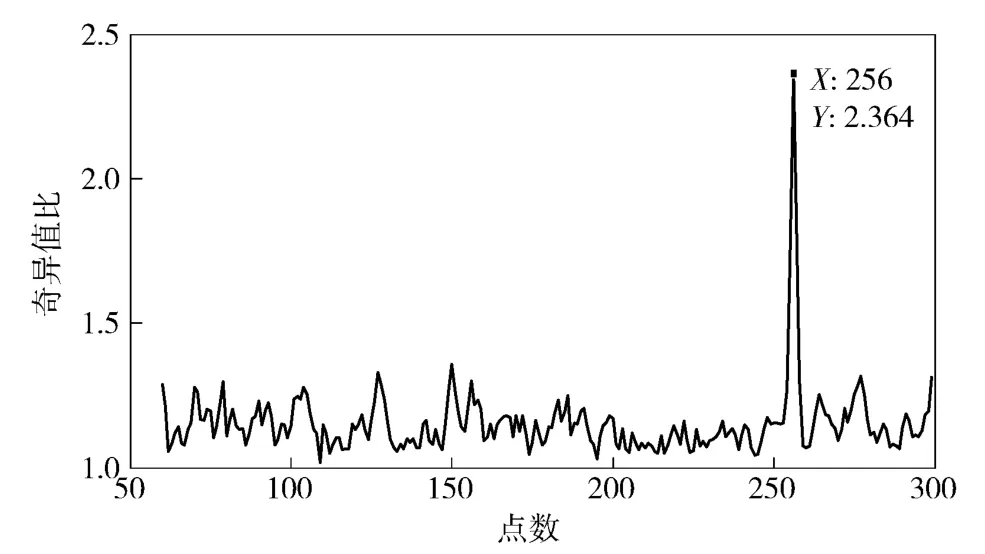
圖4 奇異值比譜示意圖Fig.4 The ratio of singular values

4.2 估計調頻率

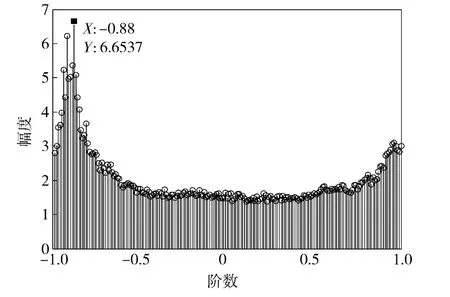
圖5 分數階傅里葉變換示意圖Fig.5 FRFT of［n］

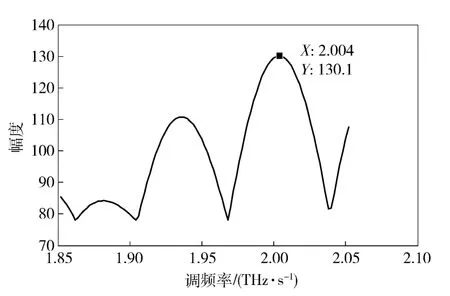
圖6 調頻率搜索示意圖Fig.6 Searching of modulation rate

4.3 估計載頻

在確定調頻率后，以2.5 節方法求解式2f0q1=以確定載頻，頻譜如圖7所示，最大值點頻率為2f0q1=4.807 MHz.

4.4 估計初始相位

4.5 估計偽碼序列

利用2.7 節方法，估計出偽碼序列，將整形前后的序列圖及源偽碼波形畫在一起，如圖8所示。

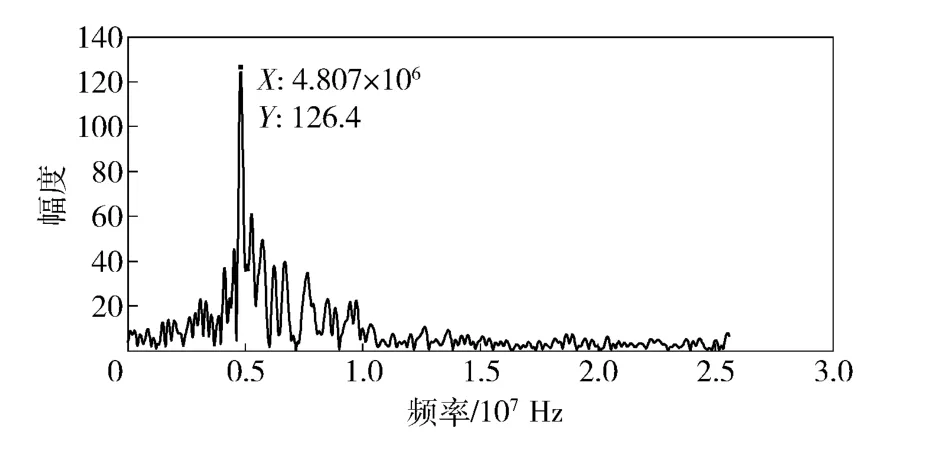
圖7 載頻估計示意圖Fig.7 Estimation of the carrier frequency

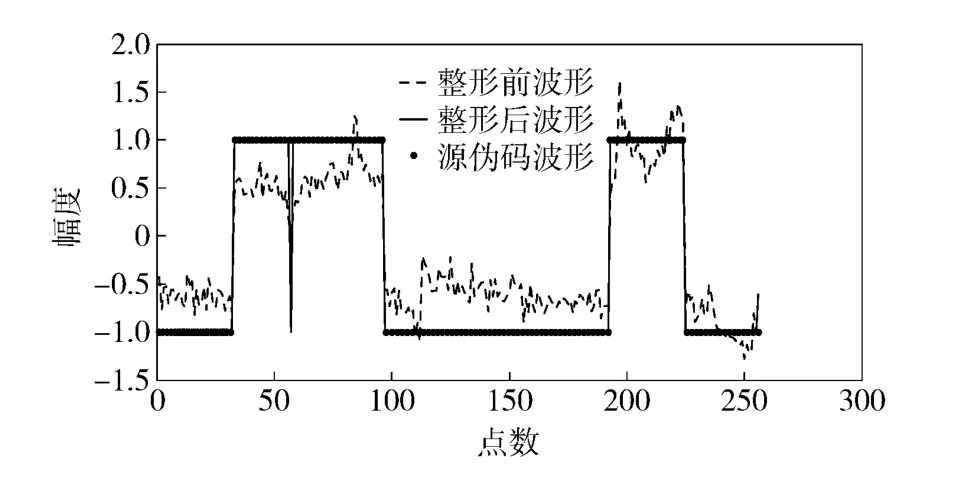
圖8 分量1 偽碼波形對比圖Fig.8 Contrast of the true and estimated pseudo random sequences of Component 1

圖8中，由于有兩個分量信號的周期相同，使用周期積累無法較好地減小同周期分量對待分離分量的干擾，造成在個別點上，受到了其他分量信號偽碼跳變的影響，致使估計出的待分離信號偽碼波形存在奇異值點，如圖8中56 點位置所示的一個跳變。為避免這種影響，在整形處理后，可以設定一個延遲參數，當波形在±1 跳變后，連續多個點都一直保持為跳變后的值，才認為這是一個偽碼跳變位置，否則判定為跳變前的值。

具體步驟為:對于整形后的一個重復周期的偽碼波形U'q［n］，給定一個延遲參數nb(本文仿真中nb=3)，重新給出一個偽碼波形U″q［n］，滿足:

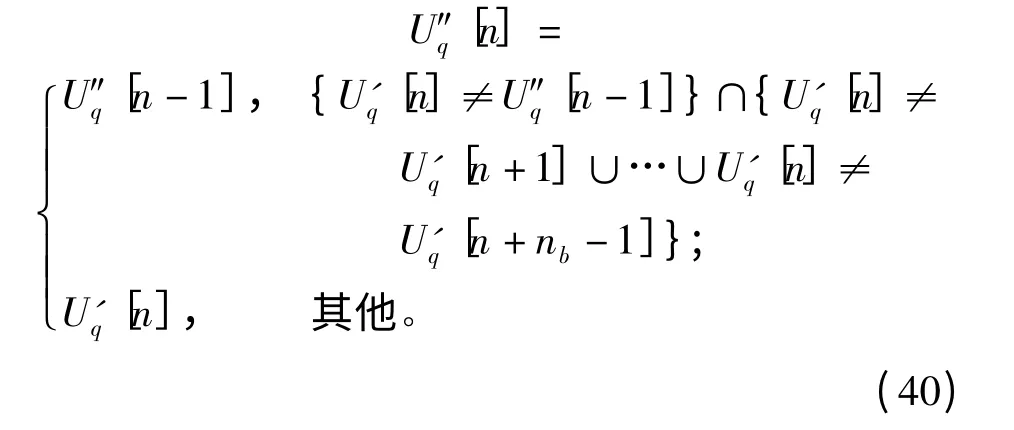
通過(40)式，可以消除圖7中的奇異值點，還原出源偽碼波形，所以，這里令U″q［n］為最后估計出的偽碼波形。

4.6 估計幅度

通過未整形前的偽碼波形，利用式Aq1=估計出幅度值為0.590 3.

4.7 波形對比

利用估計出的參數及偽碼序列，重構信號并同源信號進行對比如圖9所示，波形恢復效果較好。

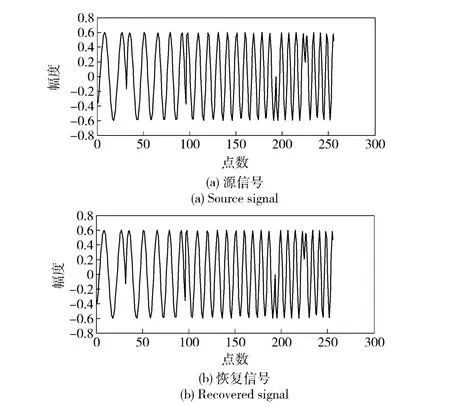
圖9 分量1 恢復信號同源信號波形對比Fig.9 Contrast of the recovered and source signals of Component 1

需要說明的是，本文算法在分離出一個分量并估計出其所有參數時，需要進行約3M + N +次復數乘法和次復數加法，其中M為混合信號長度，N 為得到的分量信號周期點數，2Δk為參考因子kc變化范圍，σ 為求解調頻斜率時的kc搜索步進，P 為進行FRFT 時的階數采樣點數，仿真時，分解一個分量并估計其相應參數的平均時間約為0.86 s，具有較高的運算效率，適用于實際應用。

對于剩余信號，這里不再具體說明各步步驟，將最后求得的偽碼對比圖和信號波形對比圖給出，如圖10～圖13所示。

圖10和圖12中，由于分解出第一個分量之后，剩余的分量信號周期不相同，能夠通過周期積累減小彼此之間的干擾，因此最后得到的偽碼波形沒有奇異值點;而圖11和圖13中，可以看出恢復波形同源波形很相似。恢復信號同源信號的各參數對比如表2所示。

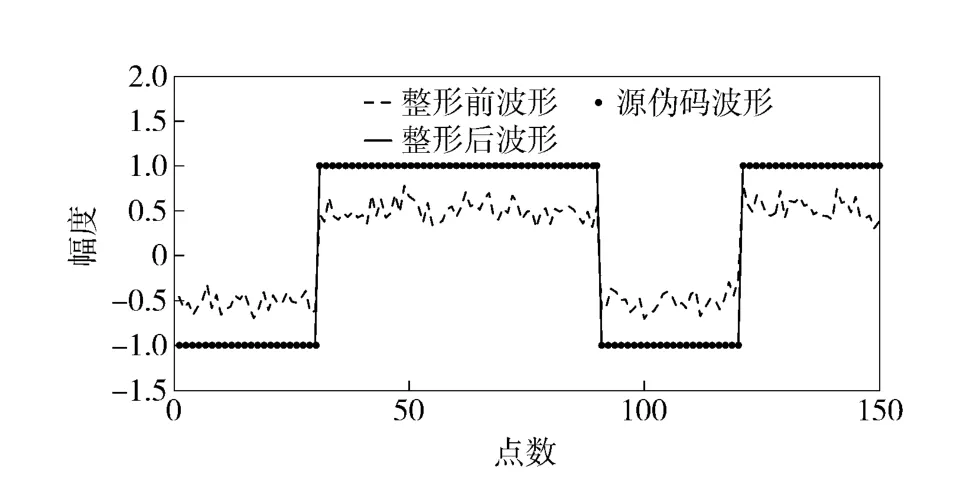
圖10 分量2 偽碼波形對比圖Fig.10 Contrast of the true and estimated pseudo random sequences of Component 2

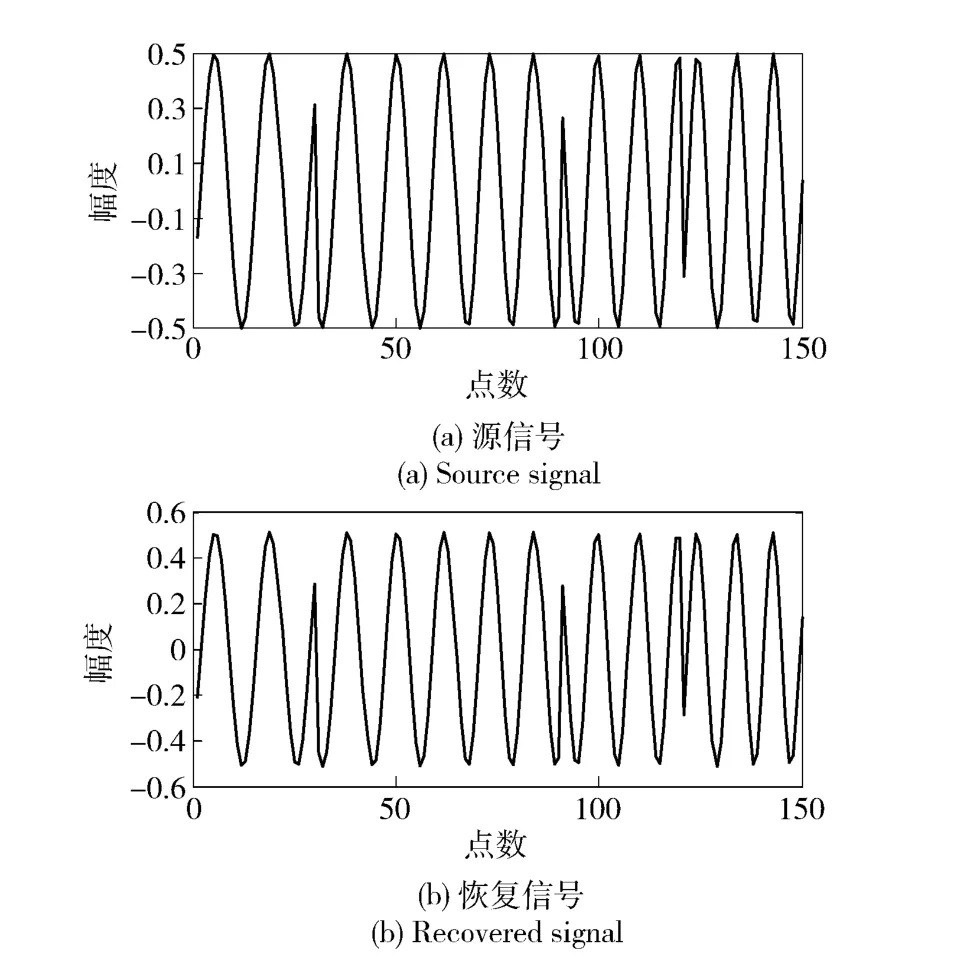
圖11 分量2 恢復信號同源信號波形對比Fig.11 Contrast of the recovered and source signals of Component 2

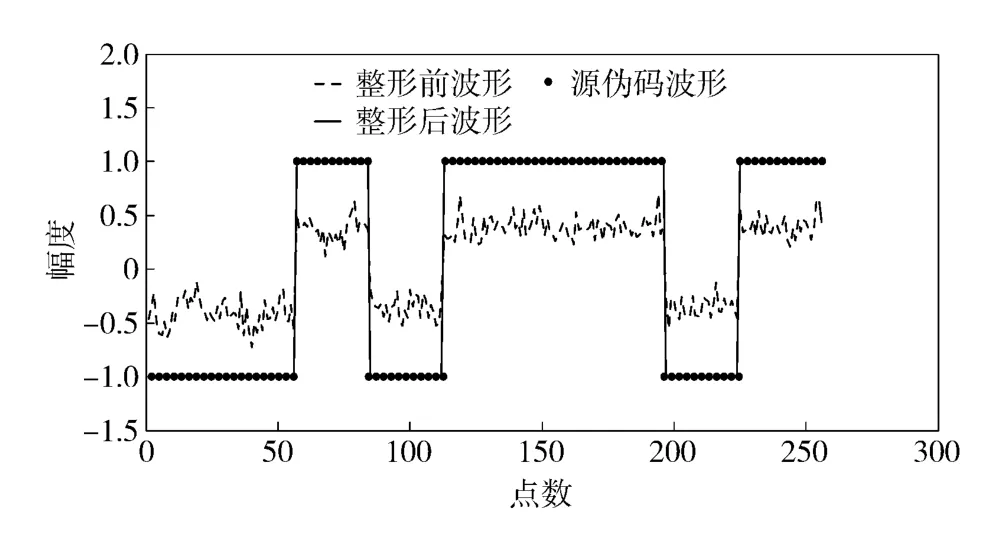
圖12 分量3 偽碼波形對比圖Fig.12 Contrast of the true and estimated pseudo random sequences of Component 3

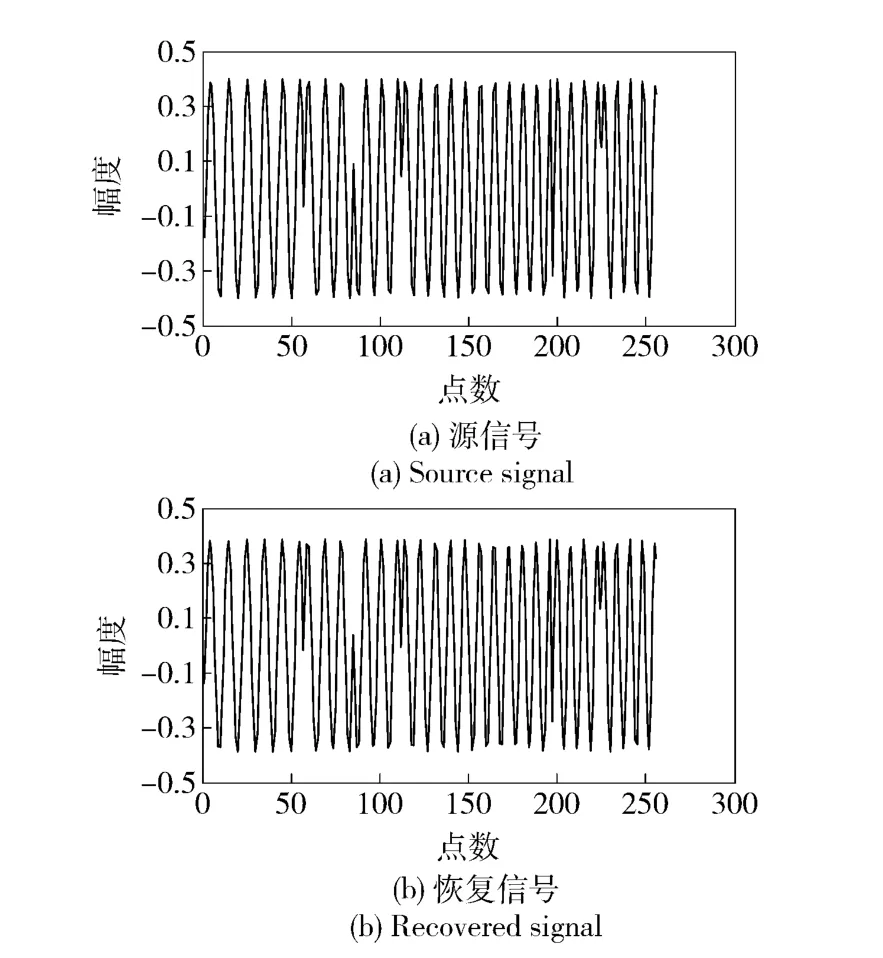
圖13 分量3 恢復信號同源信號波形對比Fig.13 Contrast of the recovered and source signals of Component 3

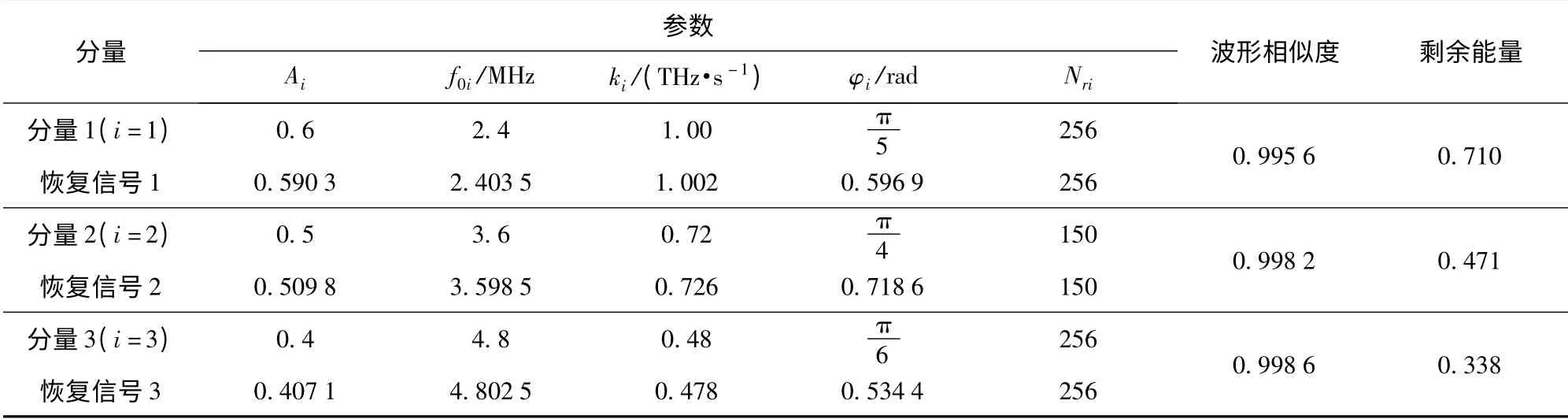
表2 各分量估計參數與原參數對比Tab.2 Contrast of the estimated and source parameters

在表2中，波形相似度用以下公式表示:

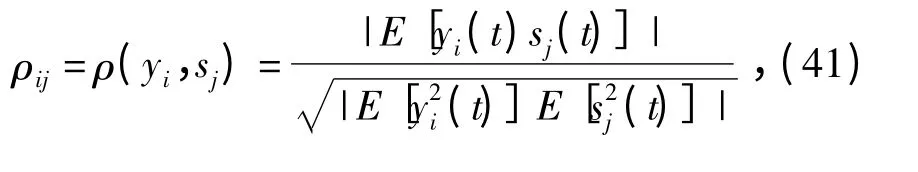
式中:ρij表示相似度系數;yi(t)和sj(t)表示求相似度的兩個信號;E［·］表示求解期望值。

從表2中可以看出，第一次及第二次分解完成之后，剩余信號能量均大于閾值，需要繼續重復步驟進行分解;當第三次分解完成之后，剩余信號能量0.338 小于閾值0.378 1，可以停止分解。

為了衡量不同輸入信噪比對這些參數估計的影響，下面畫出一般情況下，對應于不同輸入信噪比時，該方法成功估計出各參數相對于真實值歸一值的均方誤差曲線。從圖14中可以看出，這4 個參數隨輸入信噪比SNR 的增大，估計誤差NMSE 將減小。

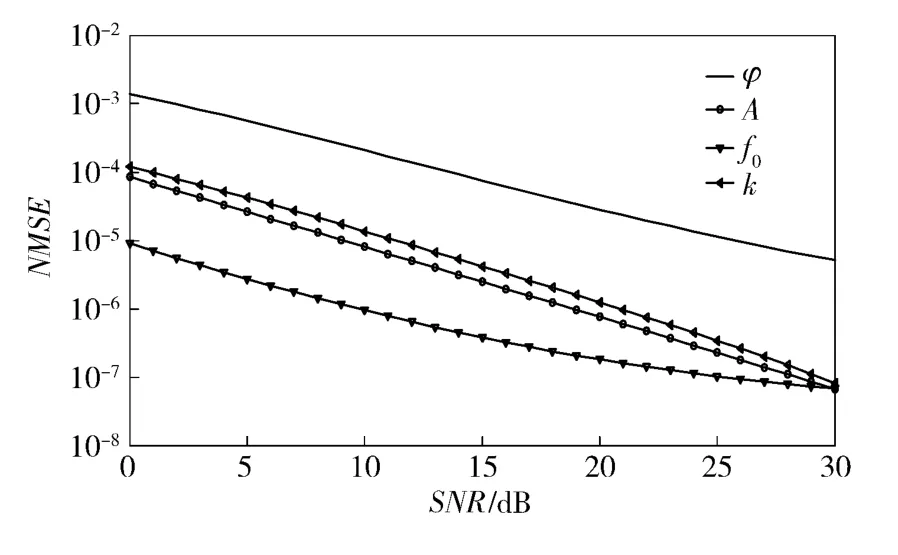
圖14 不同信噪比條件下參數估計精度Fig.14 The estimation precision of parameters under different SNRs

為了說明自適應閾值設定的有效性，圖15給出在不同信噪比條件下，各次分解后剩余能量及閾值相對于初始總能量比值曲線。從圖15中可以看出，由于采用了自適應的閾值設定，使得閾值曲線隨著輸入信噪比的變化而變化。然而，選擇不同的δ 值時，其閾值變化曲線也不同。

當信噪比較小時，由于噪聲能量占觀測混合信號能量的比重較大，使得各次分解后的能量曲線相距較近，此時信噪比估計誤差對閾值的影響較大，即使δ 取不同值，都容易出現閾值曲線不在最后兩次分解后剩余能量曲線的中間，導致分解不完全或分解不停止的情況。同樣能夠從圖15中看出，由于閾值曲線隨δ 的變小而下移，為了在信噪比較低時保證分解的成功，通常取較大的δ 值(如圖中的δ =0.20)，那么就容易無法分解出混合信號中能量較小的分量。

而當信噪比不至于過低時(＞0 dB)，由于噪聲信號能量所占的比重減小，使得各次分解后剩余能量的曲線相距較遠，那么δ 值的選擇范圍較大，此時就不容易出現分解不完全或分解不停止的情況，可以取較小的值(如圖中的δ=0.05)使得容易分解出混合信號中能量較小的分量。

綜上所述，對于絕大多數非極端情況下(信噪比不至于過低，各分量信號能量不至于太小)的混合信號，用本文方法進行信號分離和參數估計，能夠保證分解的成功和參數估計的較高精確度。

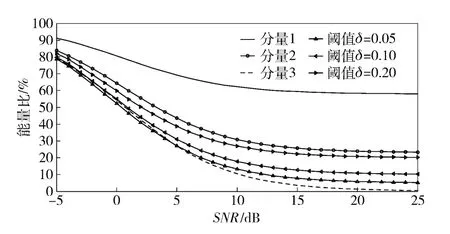
圖15 不同信噪比條件下的閾值曲線Fig.15 The curves of threshold values under different SNRs

為了衡量不同信噪比下的本文方法的效果，圖16給出了不同信噪比條件下，對于300 組不同的參數，最后能夠將各分量信號全部分離出并最后停止分解的成功率，可以發現:當信噪比大于0 dB 時，成功率大于50%;當信噪比大于3 dB 時，成功率大于90%. 可以認為該方法即使是在處理信噪比較低的情況時，也能達到較好的效果。

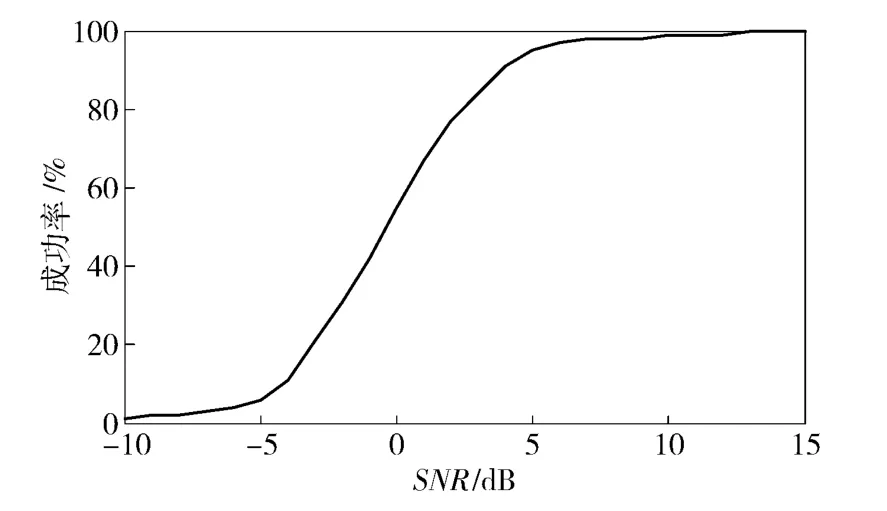
圖16 不同信噪比條件下的成功率Fig.16 The success rate under different SNRs

5 結論

本文提出一種噪聲條件下多分量PRBC-LFM信號的分離和參數估計方法，該方法通過平方計算消除偽碼影響，能夠利用PRBC-LFM 信號的周期性通過周期積累減小干擾，而后利用搜索和內積計算進行參數估計，最后利用偽隨機碼序列為實信號的特點，估計出偽碼。本文還利用自相關矩陣特征值分解估計混合信號的信噪比，從而自適應地確定停止分解的閾值。仿真結果表明，本文方法能夠對信噪比做到較好的估計，從而得到合適的閾值，且在不同信噪比條件下，對各參數的估計都能達到較好的精度，也能夠估計出偽隨機碼序列，很好地完成信號分離和參數提取。

References)

［1］ Gini F，Giannakis G B. Frequency offset and timing estimation in slowly-varying fading channels:a cyclostationary approach［J］.IEEE Trans on Communication，1998，46(3):400 -411.

［2］ Mazzenga F，Vatalaro F. Parameter estimation in CDMA multi-user detection using cyclostationary statistics［J］. Electronics letters，1996(2):179 -181.

［3］ Gardner W A，Spooner C M. Detection and source location of weak cyclostationary signals:simplifications of the maximum-likelihood receiver［J］. IEEE Trans on Communication，1993，41(6):905 -916.

［4］ Chin-Kang C，Gardner W A. Signal-selective time-difference-ofarrival estimation for passive location of man-made signal sources in highly corruptive environments(I)—theory and method［J］.IEEE Trans on Signal Processing，1992，40(5):1168 -1184.

［5］ 熊剛，趙惠昌，王李軍. 偽碼-載波調頻偵察信號識別的譜相關方法(Ⅱ)——偽碼-載波調頻信號的調制識別和參數估計［J］. 電子與信息學報，2005 ，27 (7):1087 -1092.XIONG Gang，ZHAO Hui-chang，WANG Li-jun. Reconnaisance signal recognition of PN code-carrier FM based on spectral correlation method(Ⅱ)—the modulation recognition and parameter estimation of PN code-carrier FM［J］. Jounal of Electronics ＆ Information Technology，2005，27(7):1087 -1092. (in Chinese)

［6］ 趙惠昌，熊剛，楊小牛. 基于譜相關的正弦調頻和脈間偽碼調相復合體制偵察信號識別［J］. 兵工學報，2006 ，27(2):258 -264.ZHAO Hui-chang，XIONG Gang，YANG Xiao-niu. Signal recognition of sine FM and interpulse pseudo code PM based on spectral correlation method［J］. Acta Armamentarii，2006，27(2):258 -264. (in Chinese)

［7］ 林俊，熊剛，王智學. 基于時頻分析的偽碼與線性調頻復合體制偵察信號參數估計研究［J］. 電子與信息學報，2006，28(6):1045 -1048.LIN Jun，XIONG Gang，WANG Zhi-xue. Study on reconnaissance signal parameter evaluation of PN and LFM based on time-frequency analysis［J］. Jounal of Electronics ＆ Information Technology，2006，28(6):1045 -1048. (in Chinese)

［8］ 熊剛，楊小牛，趙惠昌. 基于平滑偽Wigner 分布的偽碼與線性調頻復合偵察信號參數估計［J］. 電子與信息學報，2008，30(9):2115 -2119.XIONG Gang，YANG Xiao-niu，ZHAO Hui-chang. Parameter estimation of reconnaissance signal combined PN and LFM based on smoothed pseudo wigner distribution［J］. Jounal of Electronics ＆ Information Technology，2008，30(9):2115-2119. (in Chinese)

［9］ 李明孜，趙惠昌. 基于改進B 分布自適應窗長時頻分析的偽碼調相-載波調頻復合引信信號的參數提取研究［J］. 兵工學報，2011，32(5):543 -547.LI Ming-zi，ZHAO Hui-chang. Research on parameters extraction of pseudo code phase modulation-carry frequency modulation combined fuse signal based on the adaptive window length of improved B distribution［J］. Acta Armamentarii，2011，32(5):543 -547. (in Chinese)

［10］ Kanjilal P P. Fetal ECG extraction from single-channel maternal ECG using singular value decomposition［J］. IEEE Trans on Biomedical Engineering，1997，44(1):51 -59.

［11］ 齊林，陶然，周思永，等. 基于分數階Fourier 變換的多分量LFM 信號的檢測和參數估計［J］. 中國科學:E 輯，2003，33(8):750 -759.QI Lin，TAO Ran，ZHOU Si-yong，et al. Multicompoment LFM signal detection and parameter estimation based on fractional Fourier transform［J］. Science in China:Series E，2003，33(8):750 -759.(in Chinese)

［12］ 張金成，彭華. 一種魯棒的基于子空間分解的盲信噪比估計方法［J］. 數據采集及處理，2011，26(5):609 -614.ZHANG Jin-cheng，PENG Hua. Robust blind SNR estimation method based on subspace decompositon［J］. Jounal of Data Acquisition and Processing，2011，26(5):609-614. (in Chinese)