一種抗海浪擾動實時控制信號濾波方法
趙 江, 肖昌美, 雷霏霖, 江 濤, 王 超
?
一種抗海浪擾動實時控制信號濾波方法
趙 江, 肖昌美, 雷霏霖, 江 濤, 王 超
(海軍裝備研究院, 北京, 100161)
為了克服伺服控制系統中濾波效果與系統相位裕度不能兼顧, 消除高頻噪聲會損失有用低頻信號的問題, 以卡爾曼濾波算法為基礎, 提出了一種抗海浪用實時控制信號濾波方法, 該方法運用狀態空間法描述系統, 采用2階自回歸模型計算系統參數, 以遞推算法實現計算機實時處理, 從而達到大幅降低信號高頻噪聲, 抑制陀螺漂移, 提取有用信號的目的。仿真結果表明, 該濾波方法簡單, 實現方便, 抑制性好, 可有效減小系統的相位損失, 消除了高頻干擾, 對提高系統帶寬與系統開環增益有很大貢獻。
高頻噪聲; 實時控制; 擾動
0 引言
陀螺儀是廣泛應用于提供慣性空間基準方向的裝置。陀螺以及用陀螺構成的穩定平臺都具備穩定與跟蹤的功能, 這是由陀螺的進動性和定軸性決定的。海上各種平臺或浮標中, 一般采用陀螺穩定平臺來隔離載體擾動的影響。但是光纖陀螺的穩定性較差, 主要體現在零偏穩定性、零偏溫度靈敏度、隨機游走等指標中。陀螺的輸出噪聲和隨機游走會直接影響到陀螺穩定平臺或浮標伺服系統低速情況下的控制精度和系統的隨機漂移。特別當伺服系統在低速輸入下工作時, 未經濾波處理的陀螺輸出噪聲分量的標準偏差值甚至高于陀螺的期望輸出值, 使得陀螺輸出信噪比顯著降低, 期望輸出信號淹沒于陀螺輸出噪聲中。伺服系統輸出除了跟隨輸入信號外, 還要跟隨陀螺的輸出噪聲, 控制效果受噪聲影響較大, 伺服精度下降。且陀螺自身的漂移包括常值漂移、量化噪聲、角度隨機游走、零偏不穩定性等影響陀螺穩定平臺或浮標的漂移補償。采用實時補償的方法可有效去除常值漂移, 但對量化噪聲、角度隨機游走、零偏不穩定性構成的隨機噪聲卻無能為力。光纖陀螺輸出中包含的隨機噪聲, 常規的漂移補償方法不能滿足系統穩定性要求。上述的2個問題是光纖陀螺應用中必須解決的。傳統的滑動平均濾波技術應用可以適當減小陀螺輸出噪聲, 但效果不理想, 無法很好解決漂移問題。
本文針對光纖陀螺輸出噪聲大、隨機漂移難抑制, 普通濾波算法對陀螺穩定平臺伺服系統的控制精度造成的影響, 提出了一種抗海浪擾動光纖陀螺卡爾曼濾波方法, 該方法利用基于2階自回歸模型卡爾曼濾波技術來過濾光纖陀螺的高頻噪聲抑制系統的隨機漂移, 能有效消除陀螺高頻噪聲, 提高系統的低頻性能。
1 算法的主要內容及步驟
該方法優選實施是針對實時控制信號的濾波算法, 通過控制系統中伺服控制軟件包實現的, 其中軟件包根據圖1流程來完成。具體包括: 構建濾波模型; 計算第1步中的矩陣參數; 噪聲分析; 建立濾波遞推方程; 由建立的遞推方程, 對控制信號進行濾波, 將濾波后信號帶入系統控制回路等內容。
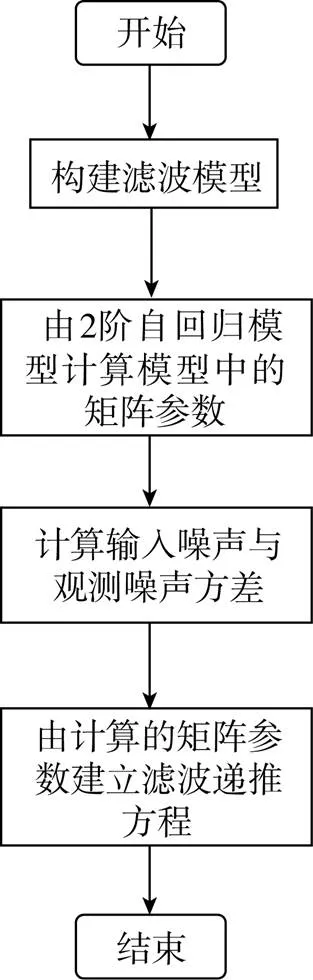
圖1 濾波器建立過程流程圖
1.1 構建濾波模型
卡爾曼濾波是用狀態空間法描述系統的, 由狀態方程(1)和測量方程(2)組成。卡爾曼濾波用前1個狀態估計值和最近1個觀測數據來估計狀態變量的當前值, 并以狀態變量估計值的形式給出
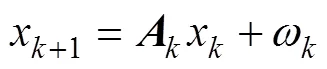
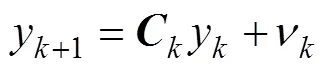
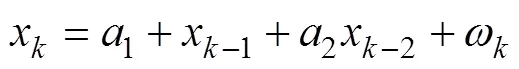
1.2 計算第1步矩陣中的參數
采用時間序列法的2階自回歸模型來描述陀螺在系統中的靜態輸出, 設狀態方程為
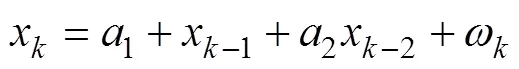
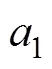
1.3 噪聲分析
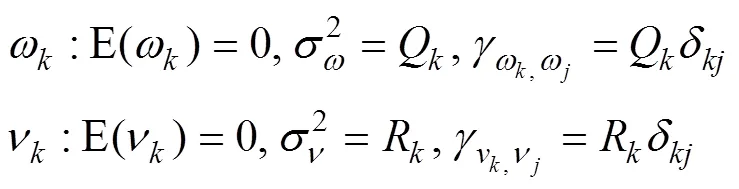
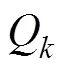
1.4 建立濾波遞推方程
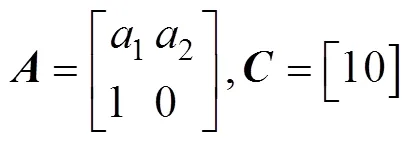
卡爾曼濾波遞推公式
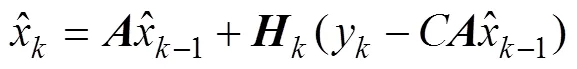
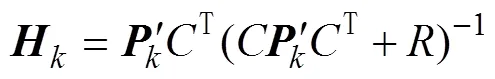
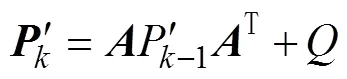
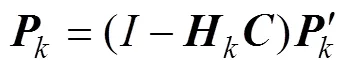
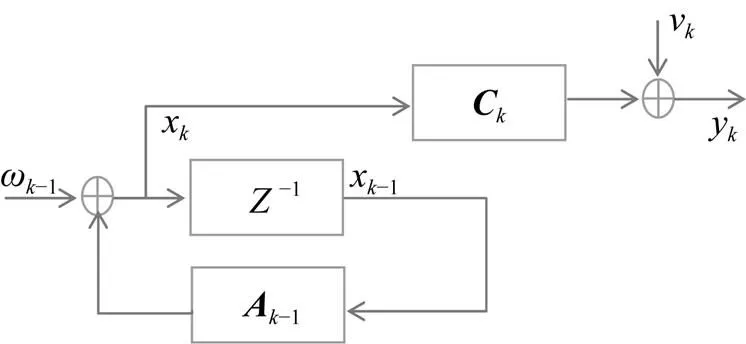
圖2 建立濾波器遞推信號流程圖
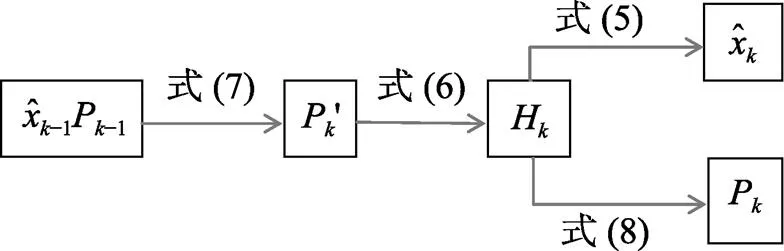
圖3濾波方程遞推過程圖
由建立的遞推公式, 對控制信號進行濾波, 將濾波信號帶入系統控制回路。
2 仿真結果及分析
以某型光纖陀螺為例, 通過采用上述方法對該型光纖陀螺建立濾波模型, 并使用該模型對此光纖陀螺的靜態噪聲和疊加噪聲分別進行濾波。對靜態噪聲濾波結果顯示, 濾波后方差是濾波前方差的0.335倍; 對疊加隨機噪聲濾波結果顯示, 濾波后方差是濾波前方差的0.201倍。其濾波前后對比如圖4、圖5所示。
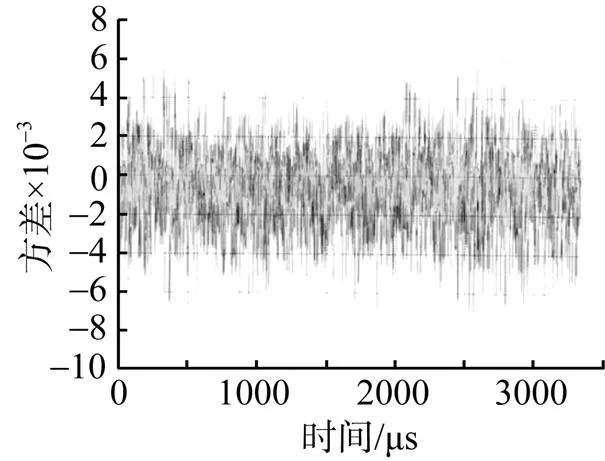
圖4 靜態噪聲波形圖
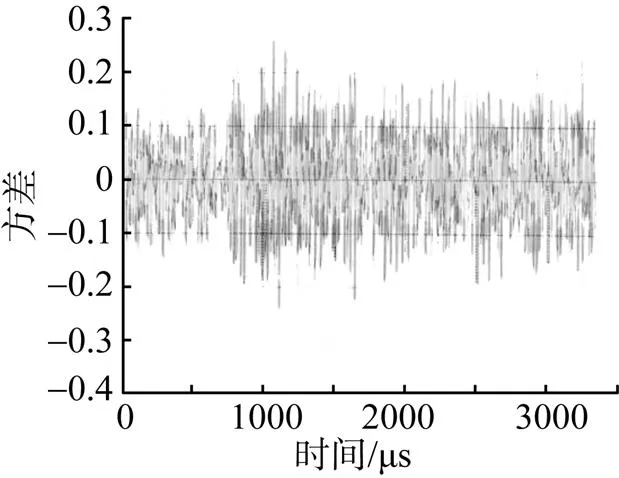
圖5 疊加隨機噪聲波形圖
分別采用滑動平均濾波器, 步長設為5步, 數字2階低通濾波器, 頻率為120 Hz以及卡爾曼濾波器, 對光纖陀螺的靜態噪聲進行濾波, 結果如圖6所示(圖的中間部分為濾波后波形)。
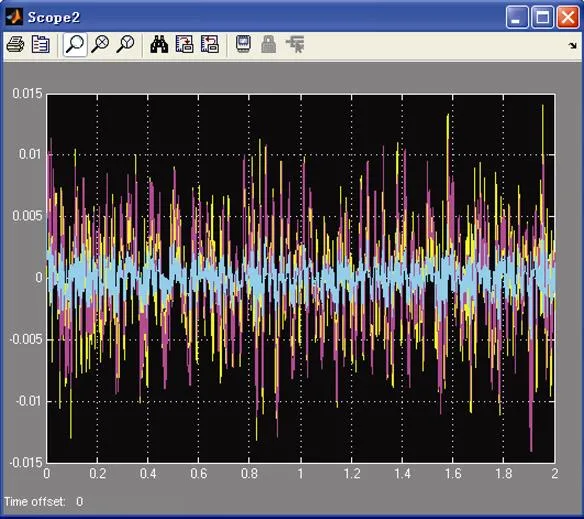
圖6 不同濾波算法結果比較
將上述3種濾波器加入伺服控制系統, 在相同的控制器下, 仿真結果如圖7所示。可見, 3種濾波器對系統開環頻響曲線的幅值影響區別不大, 但相位影響區別較大。在20 Hz處, 采用卡爾曼濾波器的相位為–104°, 采用滑動濾波器的相位為–123°, 采用2階低通濾波器的相位為–118°。卡爾曼濾波的相位裕度較大, 還可以繼續提高系統開環增益。系統閉環仿真如圖8所示, 不同濾波器對系統閉環帶寬影響不大。
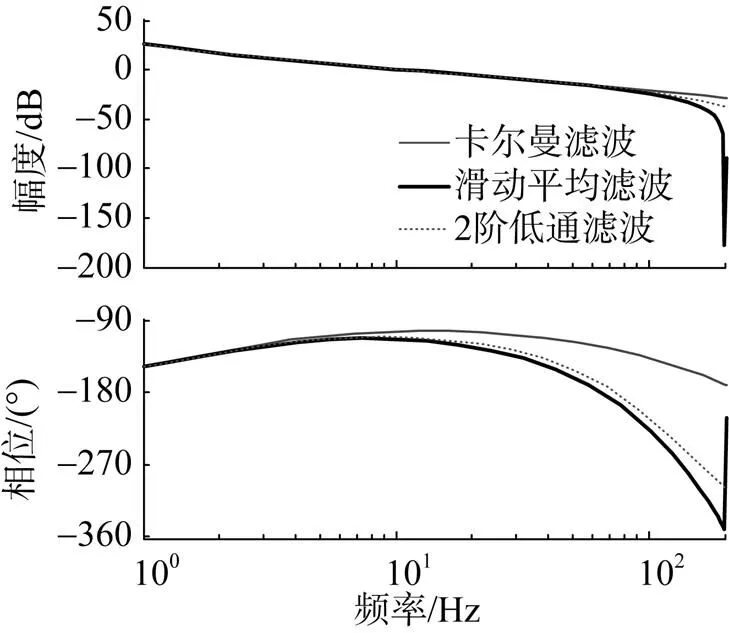
圖7 不同濾波器對系統相位的影響
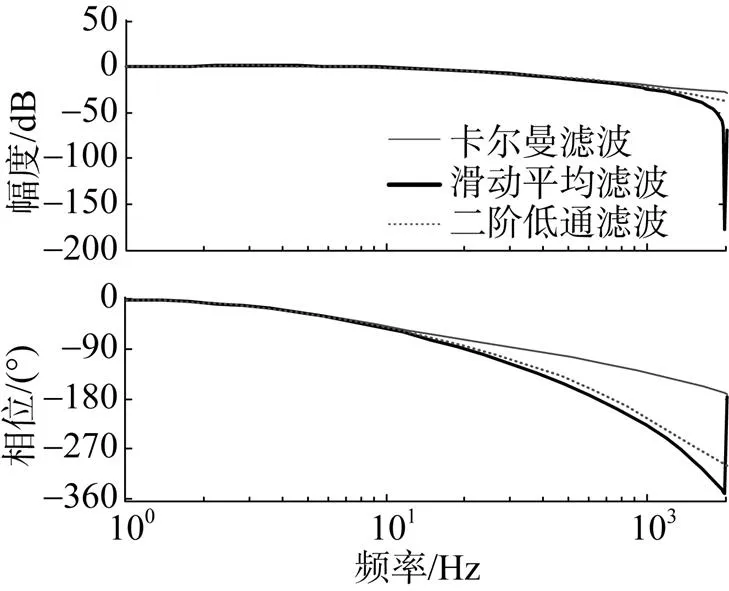
圖8不同濾波器對系統閉環曲線的影響
3 結束語
綜上所述, 本算法的預期效果體現在以下幾個方面: 通過對光纖陀螺建立濾波模型, 針對噪聲特性進行濾波, 使得本算法能消除高頻干擾, 有效抑制漂移; 該方法以卡爾曼濾波為基礎, 由2階自回歸模型計算濾波參數, 相比于其他濾波方法, 減小了系統的相位損失, 可以提高系統開環增益, 有利于提高控制系統的動態性能; 該方法中的濾波算法簡單, 實現方便, 移植性好, 具有廣闊的應用前景。
[1] 鄧自立. 卡爾曼濾波與維納濾波[M]. 哈爾濱: 哈爾濱工業大學出版社, 2001.
[2] 鄭大鐘. 線性系統理論[M]. 北京: 清華大學出版社, 2002.
[3] Anderson B D O, Moore J B. Optimal Filtering[M]. New York: Prentice Hall, Englewood Cliffs, 1979.
[4] Kalman R E. A New Approach to Linear Filtering and Prediction Problem[J]. Transactions of the ASME, Journal of Basic Engineering, 1960, 84(5): 35-45.
(責任編輯: 楊力軍)
A Filtering Method of Anti-waves Disturbance Real-time Control Signal
Zhao JiangXiao chang-meiLei fei-linJiang taoWang chao
(Naval Academy of Armament, Beijing 100161, China)
To solve the problem that filtering effect is incompatible with phase margin in servo control system, while eliminating high-frequency noise will lose useful low-frequency signal, we present a filtering method of anti-waves disturbance real-time control signal based on Kalman filter algorithm. In this method the system is described by state space method, the second-order autoregression model is used to calculate the system parameters, and recursive algorithm is adopted to achieve real-time process of computer, thus the high-frequency noise can be significantly removed, the gyro drift can be suppressed and the useful signal can be extracted. Simulation result shows that this method is simple and convenient in implementation, and has good disturbance suppression performance. Moreover, it effectively reduces the loss of system phase, eliminates the high-frequency interference, and greatly contribute improvement to the system bandwidth and the open loop gain.
high-frequency noise; real-time control; disturbance
TJ630.34; TB53
A
1673-1948(2014)01-0035-04
2013-05-07;
2013-09-18.
趙 江(1979-), 碩士, 工程師, 主要研究方向為武器系統與運用工程.

