基于投影尋蹤的低頻振蕩阻尼預測

黨 杰，王乙斐

0 引言

隨著電網互聯程度的不斷提高，系統規模越來越龐大，運行方式越來越復雜，低頻振蕩問題日漸凸現，已成為危及大規模互聯電網安全穩定運行的主要因素之一［1～5］。

近年來，國內外的學者對低頻振蕩起振的條件和機理以及抑制的措施等方面進行了不斷的探索和詳細的分析，也取得了大量的研究成果［6～10］;然而由于互聯電網的復雜性，低頻振蕩問題仍未得到有效解決。筆者認為，應借鑒電力系統三道防線的概念，分別從以下3 個階段對低頻振蕩現象進行認知、預防和控制:其一，在發電側設計合理的防止低頻振蕩的勵磁控制;其二，利用低頻振蕩在線預警系統進行預防控制;最后，當低頻振蕩事故發生時，采取緊急控制防止事故蔓延。

目前，研究低頻振蕩的方法主要是針對系統已檢測到的振蕩曲線判斷低頻振蕩是否發生，此類方法不能做到防患于未然。事實上，在電網的運行狀況發生改變時，如果能夠根據系統的實測數據及時掌握系統阻尼的變化情況，對低頻振蕩模式的阻尼做出準確預測，即可對電力系統可能產生的弱阻尼模式采取及時的控制措施，有效防范低頻振蕩的發生。

基于此，本文利用投影尋蹤方法，建立對低頻振蕩進行阻尼預測的數學模型，把描述電力系統運行特性的高維數據通過某種組合投影到低維子空間上，在低維空間上對數據結構進行分析。此方法成功克服高維數據的“維數災”問題，能夠對振蕩模式的阻尼進行準確預測。該方法的準確性和實用性在華中電網的工程實際中得到了有效驗證，從而為電力系統低頻振蕩問題的解決創造了條件。

1 投影尋蹤基本原理

隨著科學技術的發展，高維數據的統計分析越來越普遍，也越來越重要，如遙感衛星數據、GIS 中的大量數據、電力系統中廣域測量信息系統(WAMS)的數據分析等。

多元統計分析是解決這類問題的有力工具。傳統的多元統計分析方法是建立在總體服從某種分布，比如正態分布，這個假定的基礎上的，采用證實性數據分析方法(Confirmatory Data Analysis，簡稱CDA)，即“假定—模擬—檢驗”的方法。但在實際問題中有許多數據并不滿足正態分布，需要用穩健的或非參數的方法去解決。然而，當數據維數很高時，這些方法都將面臨一些困難:隨著維數的增加，計算量迅猛增大;對于高維數據，存在高維空間中點稀疏的“維數災”，非參數方法也很難使用;低維時，穩健性能好的統計方法用到高維時穩健性變差。因此，傳統的CDA方法對于高維非正態、非線性數據分析很難得到很好的效果［11］。

投影尋蹤 (Projection Pursuit，即PP)是20世紀70 年代由美國科學家Kruskal 提出的一種用來分析和處理高維觀測數據，尤其是非線性、非正態高維數據的一類新興統計方法，是應用數學、統計學和計算機技術的學科交叉，屬前沿領域［11］。其基本思想是:利用計算機技術把高維數據通過某種組合投影到低維子空間上，尋找出能反映原高維數據結構或特征的投影;再在低維上對數據結構進行分析，以達到分析研究高維數據的目的。該方法的優勢在于:它能夠在低維子空間上進行數據分析，可成功克服高維數據的“維數災”;另外，投影尋蹤與其他非參數法一樣，雖然是以數據線性投影為基礎，但它尋找的是線性投影中的非線性結構，可用來解決某些非線性問題。

2 投影尋蹤阻尼預測模型

投影尋蹤阻尼預測模型的建模過程包括以下幾步:

(1)樣本預測因子集的歸一化處理

為消除各預測因子的量綱、統一各預測因子的變化范圍，首先必須對樣本的預測因子集進行歸一化處理。假設x'(i，j)為第i 個樣本第j 個預測因子值，則各預測因子值的樣本集為{x'(i，j)| i=1，2，…，n;j =1，2，…，p}，其中n，p分別為樣本個數和預測因子的數目。歸一化的方法有很多，如:對越大越優的預測因子可采用:

式中:xmin(j)為第j 個指標值的最小值;xmax(j)為第j 個指標值的最大值;x (i，j)為預測因子特征值歸一化后的序列。

對越小越優的預測因子可采用:

本文采用標準化值，即:

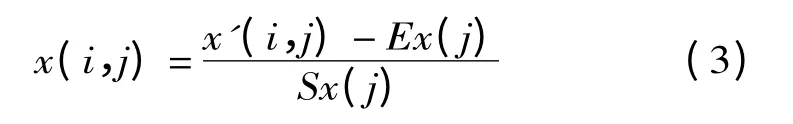
式中:Ex(j)，Sx(j)分別為第j 個預測因子x(j)的均值和標準差。

(2)構造投影指標函數Q(a)

設預測對象的樣本為{y(i)|i =1，2，…，n}，把p 維數據{x(i，j)|j =1，2，…，p}綜合成為以a ={a(1)，a(2)，…，a(p)}為投影方向的一維投影值z(i)，即:

式中:a 為單位長度向量。然后根據z(i) ～y(i)的散點圖建立適當的數學模型。

綜合投影預測因子值時，要求投影值z(i)應盡可能大地提取x(i，j)中的變異信息，即z(j)的標準差達到Sz盡可能大，即:

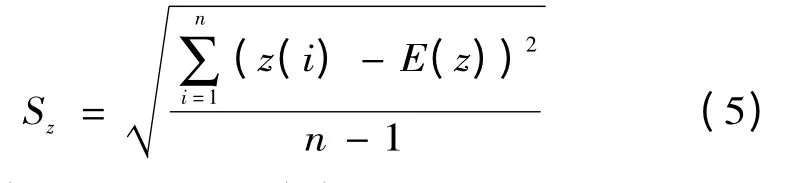
式中:E(z)為序列{z(i) | i =1，2，…，n}的平均值。

同時要求z(i)與y(i)的相關系數的絕對值| Rzy| 達到盡可能大。這樣得到的投影值就可望能盡可能多地攜帶預測因子樣本集{x(i，j)| i =1，2，…，n;j=1，2，…，p}的變異信息，并且能夠保證投影值對預測對象y(i)具有很好的解釋性;即局部投影點盡可能密集，最好凝聚成若干個點團，而在整體投影點團之間應盡可能散開。因此，投影指標函數可以構造成:

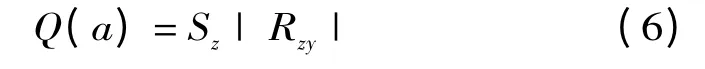
式中:Rzy為z(i)與y(i)的相關系數，即:

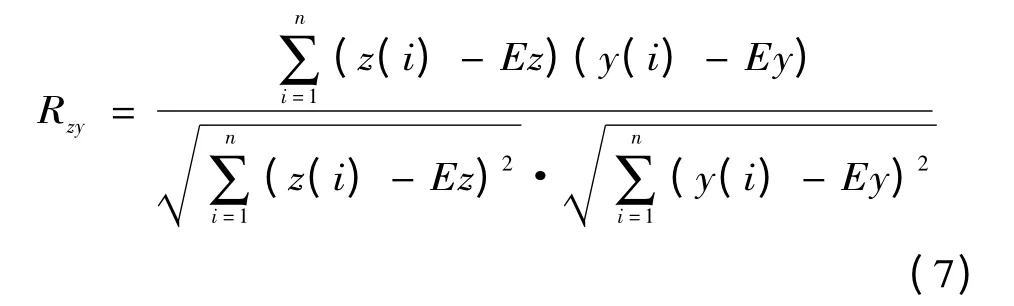
式中:Ez 和Ey 分別為序列{z(i)| i =1，2，…，n}和{y(i)| i=1，2，…，n}的平均值。

(3)優化投影指標函數

通過求解投影預測因子函數最大化問題來估計最佳投影方向，即:

這是一個以a ={a(1)，a(2)，…，a(p)}為優化變量的復雜的非線性優化問題，用傳統的優化方法處理較難;本文采用PSO 粒子群優化算法來解決全局尋優問題［12～15］。

(4)用門限回歸 (Threshold Regression，簡稱TR)模型描述投影值與預測對象之間的非線性關系

TR 模型能有效地描述具有突變性、準周期性、分段相依性等復雜現象的非線性動態系統，門限的控制作用保證了TR 模型預測精度的穩健性和廣泛的適應性。

把上一步求得的最佳投影方向a*代入式(4)后可得各樣本點的投影值z*(i)。當z*(i)～y(i)的散點圖中的點群大致呈分段線性分布時，就可采用分段線性模型來描述投影值與預測對象之間的關系。基于此，用如下TR 模型描述z*(i)～y(i)間的非線性關系:

r(0)= － ∞，r(L)= + ∞，r(j)(j =1，2，…，L－1)為門限值，L 為門限區間的個數。

e(j，i)對每一個固定的j 是固定方差的白噪聲序列。

Ez(j)，Ey(j)分別為對應z*(i)落在門限區間［r(j－1)，r(j)］中的樣本點z*(i)和y(i)的均值。

b(j)為第j 個門限區間內的回歸系數，為待定模型參數。

(5)用相關分析技術確定門限變量和門限延遲步數d

Rzy為z(i)與y(i)的相關系數，把相關系數絕對值最大的z*(i)作為門限變量，d 為y(i)與門限變量之間的時移相關系數最大值所對應的時移。

(6)確定門限區間個數L 和門限值r(1)～r(L－1)的尋優范圍

根據分段線性的段數來確定門限區間的個數L，在分段線性的轉折點附近確定各門限值r(1)～r(L－1)的搜索范圍，從而減少尋優的工作量。

大多數模型都只有兩個門限區間，此時只需對一個門限值r(1)尋優。綜合現有的文獻可知，r(1)可表征時間序列的均值特性，所以可將Ez(j)的一個領域作為r(1)的搜索范圍，計算開始時直接在此范圍尋優。

(7)用PSO 粒子群優化算法優化各門限值r(1) ～r(L－1)和各回歸系數b(j)

可以直接在模型的最小二乘估計準則下優化，即通過求解如下最小化問題來確定:

式中:y*(i)為把z*(i)代入式(9)中除白噪聲以外所得預測對象的計算值，它是各門限值r(1)～r(L－1)和各門限區間內回歸系數b(j)的函數。

(8)阻尼預測

按y*(i)值從大到小排序，可以將樣本從優到劣進行排序，知道哪種運行方式對系統阻尼較不利。

根據最佳投影方向，可以進一步分析各個預測因子對最后評價結果的影響程度，即將a*值進行排序得到各個預測因子的貢獻率大小。在此也可進一步了解哪些因素惡化系統阻尼最明顯。

3 投影尋蹤在低頻振蕩阻尼預測中的應用

將上文建立的投影尋蹤阻尼預測模型用于分析華中電網的低頻振蕩模式。表1 給出川豫振蕩模式在25 種不同運行方式下的系統阻尼y(i)，i=1，2，…，25，及其有關的5 個預測因子的值，其中5 個預測因子分別為:

z'(i，1):鄂豫斷面潮流，以鄂送豫潮流為正，豫送鄂為負。

z'(i，2):鄂湘斷面潮流，以鄂送湘潮流為正，湘送鄂為負。

z'(i，3):鄂贛斷面潮流，以鄂送贛潮流為正，贛送鄂為負。

z'(i，4):川渝斷面潮流，以川送渝潮流為正，渝送川為負。

z'(i，5):鄂渝斷面潮流，以鄂送渝潮流為正，渝送鄂為負。

首先利用表1 的25 組數據建立投影尋蹤門限回歸模型。由于樣本數量有限，用表1 中的任意24 個樣本建模，預留1 個樣本作預測。為了驗證該方法預測的準確性，第二次選擇預留另一個樣本作預測。這樣循環多次，在樣本數量有限的情況下，既可保證建模樣本的數量，又能證明預測的準確性。如表1 中，就是預留方式13 作為預測數據，其余作為建模數據，得到的結果。

把建模樣本根據式(3)轉換成標準化序列，依次代入式(4)～(8)，得到投影指標函數的值為0.630 5，最佳投影方向為a*= ［0.299 3，0.313 7，－0.063 9，0.674 7，－0.593 9］。

把a*值代入式(4)后即得各樣本點的投影值的計算值z*(i)，見表1。z*(i)～y(i)的散點圖見圖1。從散點圖可以看出，散點明顯分成2 部分，可以用門限回歸的方法用2 條直線分別擬合左右兩部分的散點。

圖1 z* (i) ～y(i)的散點圖

續表

圖1 表明，可用式(9)來描述圖1 所示的z*(i)與y (i)之間的關系。式(9)中的模型參數L=2，b (1)和b (2)通過PSO 粒子群優化算法得到。最后得到的川豫振蕩模式的阻尼預測模型為:

式中:y*(i)為與z*(i)對應的阻尼值。用式(11)進行擬合檢驗和預測檢驗，結果如表2 所示。表中擬合一欄是對24 組數據進行統計的結果，預測是對運行方式13 的統計。若預留其它方式做預測，結果也是類似的。若樣本數據的數量加大，預測和擬合的效果更好。

由表2 知:

(1)若以阻尼比小于5%的絕對誤差為合格，則阻尼預測模型的擬合合格率和預測合格率均為100%，這在工程上是完全可以接受的。

(2)若以相對誤差小于30%為合格，則除運行方式3 和運行方式4 不合格以外，阻尼預測模型的擬合合格率為92%，預測合格率均為100%;運行方式3 和運行方式4 可以看成是壞數據。

表2 阻尼預測中的擬合檢驗和預測檢驗

(3)阻尼預測模型由于有了門限的控制作用，可描述系統阻尼特性這一非線性復雜動態系統的問題。

(4)阻尼預測模型的擬合精度和預測精度是一致的，顯示出穩健的預測性能。

4 結論

本文提出了一種基于投影尋蹤的阻尼預測方法。該方法有別于已有的基于實測的低頻振蕩在線預測，不是在已檢測到的系統振蕩曲線上判斷低頻振蕩是否發生;而是對有限的系統振蕩模式進行高維數據統計分析，在事故發生前預測系統在當前運行方式下的阻尼情況，從而判斷系統是否會發生低頻振蕩，以及可能發生的低頻振蕩模式。結合華中電網工程實際驗證了該方法的有效性和準確性，從而為低頻振蕩的在線監測和預防控制提供了一種新的技術手段。

［1］朱方，趙紅光，劉増煌，等．大區電網互聯對電力系統動態穩定性的影響［J］．中國電機工程學報，2007，27(1):1-7．

［2］曾正，劉滌塵，向農，等．廣域系統低頻振蕩的諧振傳播 機 理 ［J］．電 力 科 學 與 工 程，2010，26(11):29-33．

［3］胡炳杰，趙書強，陳彩鳳．應用正規形理論的電力系統低頻振蕩分析［J］．電力科學與工程，2009，25 (2):10-12．

［4］朱方，湯涌，張東霞，等．我國交流互聯電網動態穩定性的研究及解決策略［J］．電網技術，2004，28(15):1-5．

［5］王洪濤，劉玉田，雷鳴，等．電網互聯對山東電網內部低頻振蕩模式的影響［J］．中國電力，2004，37 (6):12-15．

［6］吳海霞，常勇．低頻振蕩廣域監控研究現狀及新進展［J］．高電壓技術，2008，34 (8):1737-1744．

［7］張鵬飛，羅承廉，孟遠景，等．電力系統低頻振蕩的廣域監測與控制綜述［J］．電網技術，2006，30 (增刊):157-161．

［8］邱夕兆，于占勛，雷鳴，等．山東電網基于WAMS 的低頻振蕩統計與評估［J］．電力系統自動化，2008，32(6):95-98．

［9］鞠平，謝歡，孟遠景，等．基于廣域測量信息在線辨識低頻振蕩［J］．中國電機工程學報，2005，25 (22):56-60．

［10］韓松，何利銓，孫斌，等．基于希爾伯特—黃變換的電力系統低頻振蕩的非線性非平穩分析及其應用［J］．電網技術，2008，32 (4):56-60．

［11］付強，趙小勇．投影尋蹤模型原理及其應用［M］．北京:科學出版社，2006．

［12］唐權，吳耀武，熊信銀，等．SA-PSO 在水火電混合電力系統電源規劃中的應用［J］．高電壓技術，2006，32 (4):104-107．

［13］魏星，舒乃秋，張霖，等．基于改進PSO-BP 混合算法的電力變壓器故障診斷［J］．電力自動化設備，2006，26 (5):35-38．

［14］丁玉鳳，文勁宇．基于改進PSO 算法的電力系統無功優化研究［J］．繼電器，2005，33 (6):20-24．

［15］任沖，劉滌塵，潘曉杰，等．與三峽—萬縣輸電線路相連電網的等值簡化與實時仿真研究［J］．電力科學工程，2006，(1):15-18．