小波消噪在枯水期來水量預報中的應用

陳攀，姜志群

（1.華電四川發電有限公司寶珠寺水力發電廠，四川廣元628003；2.南京江山同和水利水電技術有限公司，江蘇南京210000）

小波消噪在枯水期來水量預報中的應用

陳攀1，姜志群2

（1.華電四川發電有限公司寶珠寺水力發電廠，四川廣元628003；2.南京江山同和水利水電技術有限公司，江蘇南京210000）

根據小波理論，將枯水期來水量序列進行小波分解，并用軟閾值方法進行消噪處理。用消噪后的小波系數進行序列重構，對重構后的序列進行時間序列分析，構建時間序列AR（p）模型，用AR（p）模型進行來水量的預測。

小波分析；枯水預測；時間序列分析；水庫

1 引言

早期枯水的研究進展較緩慢，從目前研究的內容、方法以及深度等方面來看，枯水研究遠不及洪水的研究。隨著社會經濟的發展和人口的急劇增長，人類生存和生產對水的需求十分迫切，水資源的供需矛盾日益突出，尤其是在枯水季節，這種矛盾就更加尖銳。枯水季節因河流徑流量減少水污染加重，同時人類過度開發利用枯水資源等造成河流斷流、地面下沉、海水入侵等一系列的環境問題。因此，開展枯水徑流研究和預測，揭示枯水徑流規律，對于水資源的評價計算和合理開發利用、解決枯季水資源的供需矛盾、保證經濟建設的持續穩定發展具有重要意義。

影響枯水徑流的自然因素很多，主要包括土壤巖石的類型及其滲透特性，水力特征，含水層的厚度，匯流的速度、頻率及流量，流域內的土壤水分蒸發蒸騰損失量，流域面積，植被類型，地形和氣候等。枯水徑流受單一因素影響的情況幾乎已不復存在，絕大部分是受各種直接或間接因素的復合影響。國內對枯水徑流預報和預測方面的研究方法多限于利用經驗的、比較簡單的傳統方法，主要有退水曲線法、前后期徑流相關法和河網蓄水量法、回歸分析法[1]、數理統計法、模糊數學法[2]、灰色系統法等。在新研究方法方面，人工神經網絡（LM）模型用于研究較復雜且影響因子眾多的非線性映射關系的枯水徑流問題[3]；遺傳算法原理直觀、方法簡便實用，且能更好地解決復雜模型參數的優化估計問題，為研究和建立更為復雜的枯水徑流預測模型提供了強有力的技術保證。

由于枯水期來水量小、測量誤差及其他不確定性影響因素較多，枯水期來水量本身含有較多的噪聲。本研究試圖通過小波消噪［4］來改善序列的自相關特性，并用時間序列分析進行枯水期來水量預測。

2 枯水期來水量隨機預測模型

實測水文序列含有噪聲，尤其是枯水期來水量含有較多的噪聲，這些噪聲的存在可能淹沒了水文時間序列的真實變化特性，特別是改變了序列的自相關結構，應用小波消噪方法將其噪聲消減。

2.1 水文序列的小波消噪

設水文序列xt，對其用Mallat算法進行J次小波分解，得到J尺度下的尺度系數序列和小波系數序列dt1，dt2，…，dtJ。

Mallat小波快速分解算法為：

式中：H為分解低通濾波器；G為分解高通濾波器；C為尺度系數；D為小波系數；j為分解的尺度（即分解次數）。

用Stain無偏估計法估計小波系數的閾值；利用軟閾值方法進行消噪；再用Mallat算法進行重構，得到消噪后的水文序列。

Mallat小波重構算法為：

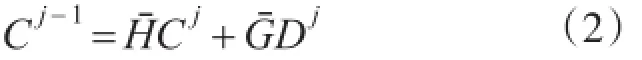
式中：Hˉ為重構低通濾波器；Gˉ為重構高通濾波器；其他符號意義同上。

2.2 隨機模型的建立

對消噪后的水文序列建立隨機模型。枯水期來水量消噪后的水文序列是平穩的，可采用AR（p）模型。

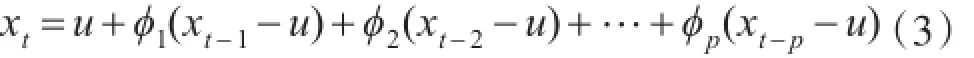
式中：u為消噪后水文序列的均值；?p為自回歸系數，p為模型階數。

模型的階數用AIC準則進行估計，即：

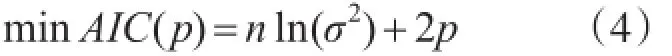
式中：n為序列長度；σ2為方差；其他符號意義同上。

3 實例研究

以四川寶珠寺水庫為例，研究其枯水期來水量預測。寶珠寺水庫位于四川省廣元市境內，以發電為主，兼有灌溉、防洪、旅游和養殖等綜合利用效益。水庫總庫容25.5億m3，調節庫容13.4億m3。

水庫枯水期來水量資料系列為1948—2012年共65年，均值35.027億m3，標準差8.32。

從枯水期來水量序列可見，序列存在明顯的趨勢項，即來水量呈遞減趨勢。所以，首先應將趨勢項分離出來，用最小二乘法以線性方程擬合趨勢項。

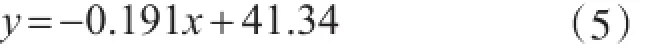
式中：y為來水量；x為時序。

由于過濾了趨勢項的殘差序列為非白噪聲序列，需對其進行白化處理，如圖1所示，即對該系列進行標準化處理。

圖1 原序列過濾趨勢項并標準化

對標準化后序列用Mallat算法進行1次小波分解，得到尺度系數序列和小波系數序列dt1，dt2，…，dtM，見表1。用Stain無偏估計法估計小波系數的閾值為0.445。用軟閾值法對標準化后序列進行消噪，如圖2所示。然后，對消噪后的小波系數用Mallat算法進行重構，得到消噪后的重構序列，如圖3所示。

原殘差序列的前4階自相關系數分別為0.0，0.0，0.07，0.13，不具拖尾性，為非平穩時間序列。重構序列的前4階自相關系數分別為0.57，0.32，0.26，0.07，具有良好的拖尾性，說明該序列為平穩時間序列。由此看來，通過小波去噪，大大改進了來水量序列的自相關特性。對重構的小波序列建立時間序列AR（p）模型。由AIC準則計算得到AR模型階數為1，模型為：

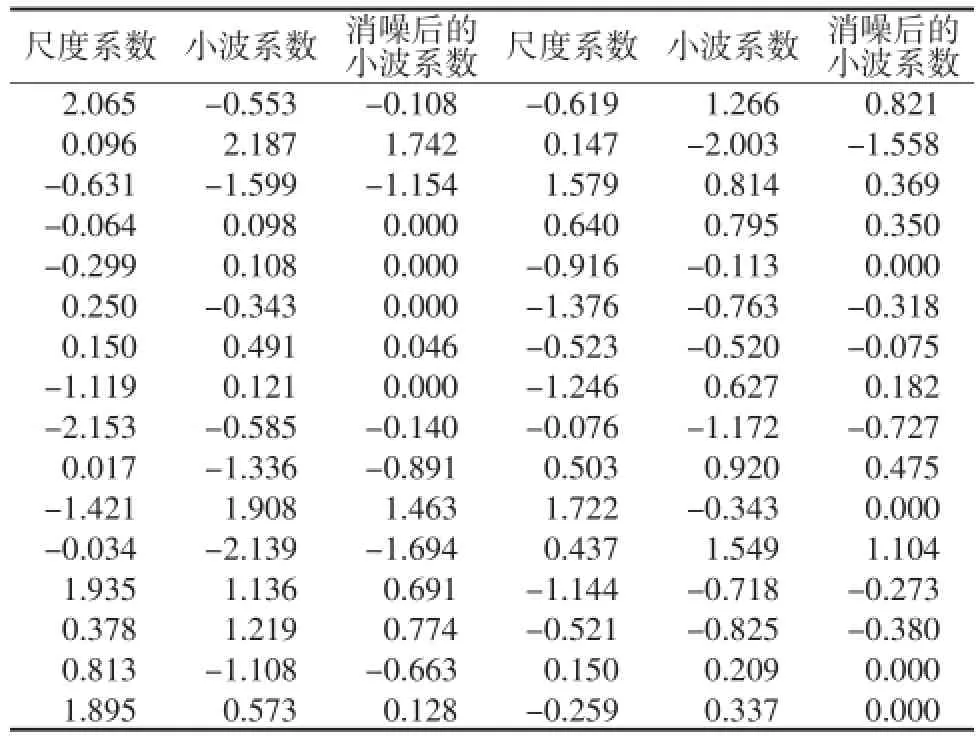
表1 小波分解后的系數和消噪后的系數

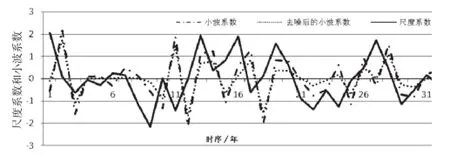
圖2 尺度系數和小波系數

圖3 原序列和重構后的序列

根據AR模型，計算得到2013年標準化后的來水量為0.066，還原為預測枯水期來水量為29.218億m3，實測2013年枯水期來水量為29.778億m3。

[1]Donald B.Percival&Andrew T Walden.時間序列分析的小波分法［M］.北京：機械工業出版社，2006.

[2]馮國章.枯水徑流預報的最優模糊劃分自激勵門限自回歸模型[J].西北農業大學學報，1997，（2）：21-26.

[3]繆益平，鄧俊.基于BP人工神經網絡的枯水徑流預報方案研究[J].水文，2008，28（3）：33-36.

[4]王文圣，丁晶.水文小波分析[M].北京：化學工業出版社，2005.

TV124；P338

B

1004-7328（2014）04-0042-02

10.3969/j.issn.1004-7328.2014.04.015

2014-03-10

陳攀（1970-），男，工程師，主要從事水文預報情報和水庫調度工作。