穩態法測量導熱系數的誤操作影響分析

柯 磊， 楊黨強， 袁艷紅

(上海電機學院 數理研究所， 上海 201306)

0 引 言

導熱系數是表征物質熱傳導性質的物理量，材料的導熱系數與材料的組分和結構有關，通常需要采用實驗的方法精確確定[1-4]。穩態法測量不良導體的導熱系數的目的是讓學生應用穩態法進行導熱系數的測量，同時學習用物體的散熱速率求傳導速率的實驗方法[5-8]。但我們在近些年的實驗教學過程中發現，學生在實驗操作中，出現了一系列誤操作行為，導致測量的導熱系數產生較大偏差。本文模擬實驗中一些常見的誤操作，并對大量實驗結果進行系統的比較，分析引起導熱系數出現偏差的主要因素，為實驗教學提供參考。

1 穩態法測量導熱系數

1898年，Lees首先使用平板法測量不良導體的導熱系數。實驗中，樣品制成平板狀，其上端面與一個穩定的均勻發熱體充分接觸;下端面與一均勻散熱體相接觸。由于平板樣品的側面積比平板面積小很多，可以認為熱量只沿著上下方向垂直傳遞，橫向由側面散去的熱量可以忽略不計，即可以認為，樣品內只有在垂直樣品平面的方向上有溫度梯度，在同一平面內，各處的溫度相同[9-10]。

設穩態時，樣品上、下平面溫度分別為θ1、θ2，根據傅里葉傳導方程[11]，在Δt內通過樣品的熱量ΔQ為

(1)

式中：λ為樣品的導熱系數；h0為樣品的厚度；S為樣品的平面面積；實驗中樣品為圓盤狀，直徑為D。

圖1為穩態法測量導熱系數的示意圖，當傳熱達到穩定狀態時，樣品上下表面的θ1和θ2不變，這時可以認為加熱盤通過樣品傳遞的熱流量與散熱盤向周圍環境的散熱量相等[12]。因此，可以通過散熱盤在穩定溫度θ2時的散熱速率來求出熱流量：

式中:m為散熱盤的質量;c為散熱盤的比熱容。

圖1 穩態法測量導熱系數示意圖

在達到穩態過程中，散熱盤的上表面并未暴露在空氣中，而物體的冷卻速率與它的散熱表面積成正比，故穩態時散熱盤散熱速率表達式應作面積修正[13]：

(2)

式中:R為散熱盤的半徑;h為散熱盤的厚度。

由式(1)、(2)可得樣品的導熱系數為

(3)

2 誤操作影響分析

在實際的實驗教學中發現，不少學生存在實驗誤操作，導致測量的導熱系數出現偏差，主要誤操作包括：樣品與加熱、散熱盤未對齊；樣品與加熱、散熱盤接觸過緊；未達到穩態時測試；未進行強迫對流換熱；熱電偶與加熱、散熱盤接觸不充分等。本文將模擬上述誤操作，分析穩態法實驗中誤操作對測量的導熱系數數值的影響。

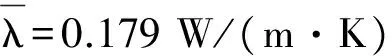
2.1 樣品與加熱、散熱盤未對齊

學生操作時最常見的一類誤操作是未將橡皮樣品與加熱、散熱盤對齊，通常未對齊的表面積比例在10%以內。分別將橡皮樣品與兩盤未對齊比例設置在5%和10%，并設置極端比例50%進行誤操作對比實驗，實驗曲線如圖2所示。從圖2可見，未對齊實驗的曲線和參考曲線相比出現了明顯的偏移，在散熱盤穩態溫度附近的曲率存在一定的偏差。結合表1實驗數據，隨著樣品與兩盤未對齊比例的增加，散熱盤穩態溫度和導熱系數均逐漸下降；在常見的未對齊比例10%的實驗中，導熱系數的百分差為6.7%，偏差較大。

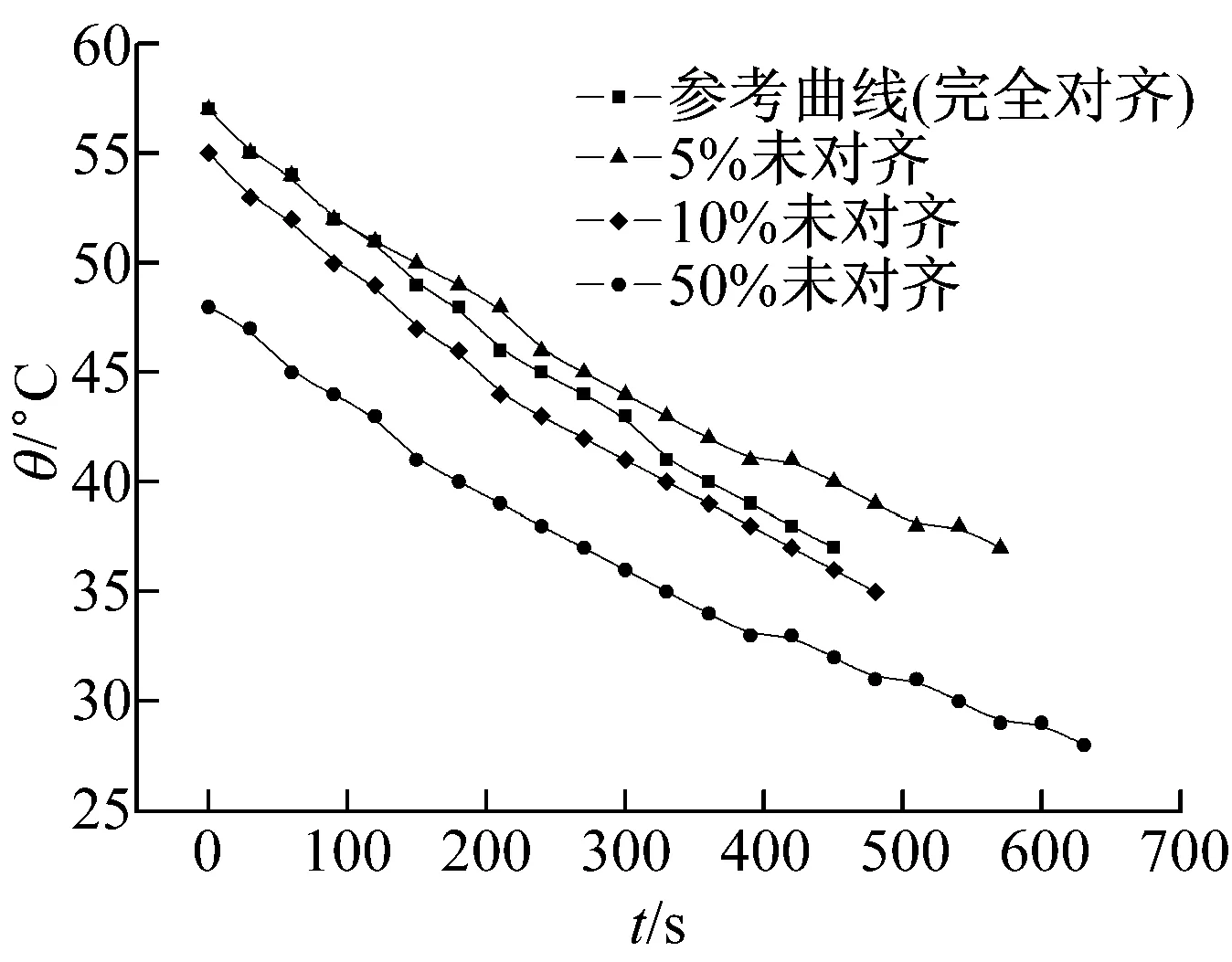
圖2 樣品與加熱、散熱盤未對齊對比實驗曲線

2.2 樣品與加熱、散熱盤接觸過緊

為了定量模擬樣品與加熱、散熱盤接觸過緊的誤操作，采取在加熱盤上方添加砝碼的方式。實驗中，添加的砝碼質量分別為0.5、1.0、2.0 kg，3組實驗數據高度一致。僅以2.0 kg的額外壓力為例來分析樣品與兩盤接觸過緊的誤操作，實驗曲線如圖3所示。從圖3可見，壓力實驗的曲線和參考曲線在散熱盤穩態溫度附近的曲率較一致，表1中實驗數據表明，導熱系數的百分差為2.2%，偏差較小。這也表明，2 kg以內的額外壓力對實驗的影響不大，樣品的導熱系數誤差較小。

2.3 未達到穩態時測試

在操作中未達到穩態時測試也是較常見的一類誤操作。根據穩態法的原理，必須得到穩定的溫度分布，這就需要較長的時間等待。不少學生在實驗中缺乏耐心，在散熱盤的溫度尚未穩定便進行數據的采集和記錄。圖4為未達到穩態時測試實驗的對比曲線圖，圖中分別模擬了低于穩態溫度1、2、3 ℃的實驗結果。從圖中可以看出，雖然未達到穩態時測試的曲線相對于參考曲線的偏移不是很大，但在散熱盤穩態溫度附近的曲率有明顯的偏差。結合表1中的實驗數據，隨著散熱盤穩態溫度的降低，樣品導熱系數大幅度下降；當散熱盤穩態溫度為44 ℃時，樣品的導熱系數降低到0.115 W/(m·K)，降低了35.8%，偏差非常大。

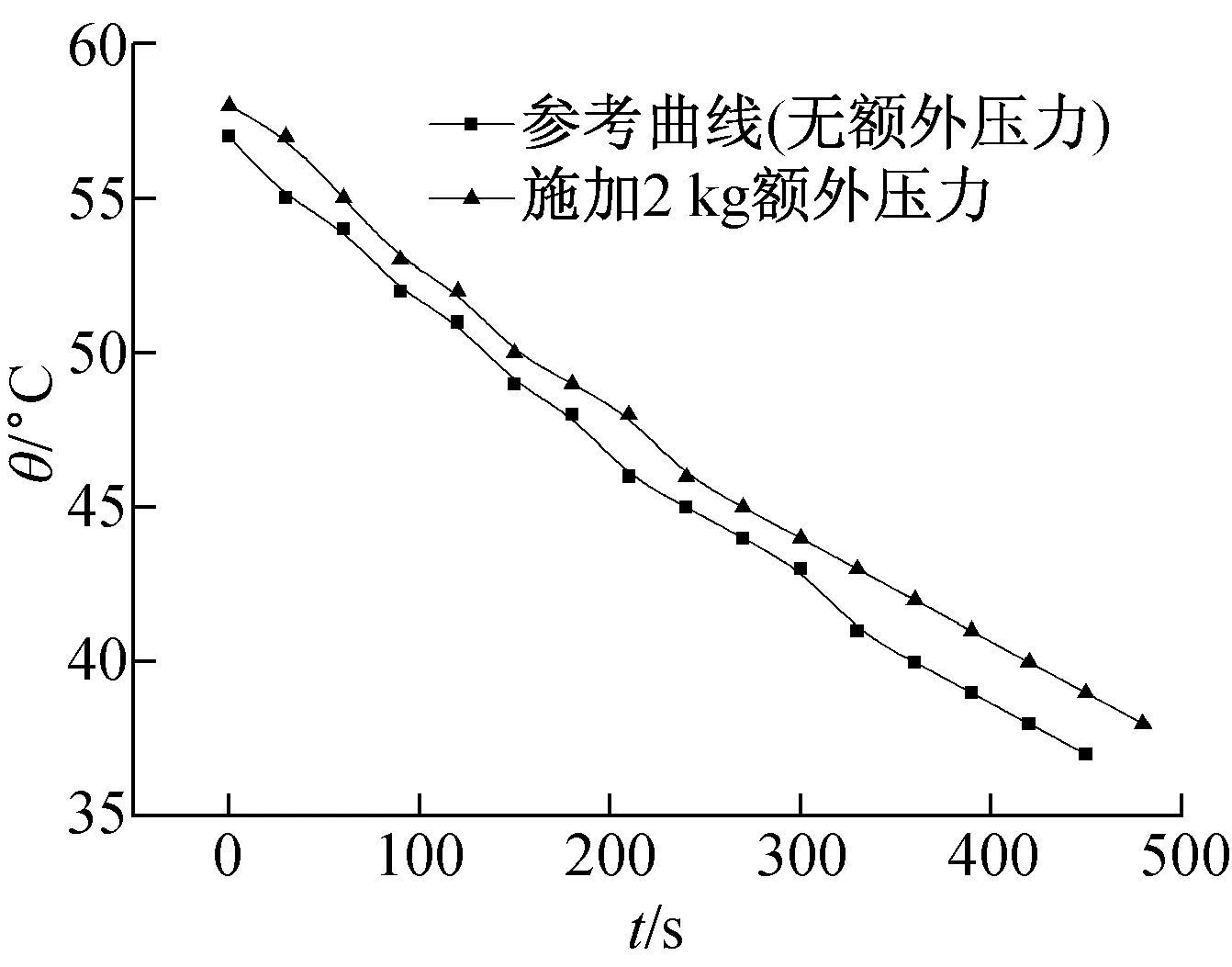
圖3 樣品與加熱、散熱盤接觸過緊對比實驗曲線

模擬誤操作名稱θ2/℃Δθ2/℃λ/(W·m-1·K-1)導熱系數百分差η/%樣品與加熱、散熱盤未對齊5%4700．177-1．1樣品與加熱、散熱盤未對齊10%45-20．167-6．7樣品與加熱、散熱盤未對齊50%38-90．093-48．0施加2kg額外壓力4810．1832．2未達到穩態時測試(θ2=46℃)46-10．163-8．9未達到穩態時測試(θ2=45℃)45-20．158-11．7未達到穩態時測試(θ2=44℃)44-30．115-35．8全程未開風扇59120．1863．9加熱過程未開風扇58110．26648．6熱電偶與加熱、散熱盤接觸不充分45-20．111-38．0

注：負值表示低于參考值

未達到穩態時測試，一方面使溫差θ1-θ2增加，另一方面較低的θ2值引起散熱盤穩態點向低溫處偏移，曲率(Δθ/Δt)|θ=θ2減小，這兩方面都會導致導熱系數降低。

圖4 未達到穩態時測試對比實驗曲線

2.4 未進行強迫對流換熱

在分析未進行強迫對流換熱對實驗的影響時，采取兩種不同的方式進行：全程未開風扇、加熱過程未開風扇。這兩種方式分別模擬整個實驗過程忘記進行強迫對流換熱，以及實驗過程中記起后再進行強迫對流換熱的情況，實驗曲線如圖5所示。從圖5可見，兩種方式均對實驗結果造成了影響，使曲線向高溫方向產生了較大的偏移。從表1的實驗數據中可以看出，兩種方式使散熱盤的穩態溫度值升高了11～12℃，其中全程未開風扇引起導熱系數的百分差只有3.9%，而加熱過程未開風扇對導熱系數的影響很大，百分差達到48.6%。

圖5 未進行強迫對流換熱對比實驗曲線

造成上述偏差的原因同樣可以從溫差θ1-θ2的變化和散熱盤穩態點處曲率(Δθ/Δt)|θ=θ2的變化兩方面來分析。全程未開風扇和加熱過程未開風扇均會使散熱盤的穩態溫度θ2升高，因此溫差θ1-θ2減小，導熱系數變大。然而，全程未開風扇的散熱過程變緩，散熱盤穩態點處的曲率(Δθ/Δt)|θ=θ2減小，導熱系數變小，縮小了溫差引起的偏差；而加熱過程未開風扇的散熱過程較快，曲率(Δθ/Δt)|θ=θ2較大，導熱系數變大，加劇了溫差引起的偏差。

2.5 熱電偶與加熱、散熱盤接觸不充分

實驗中需在熱電偶上均勻涂抹硅脂[15]，并要求插到加熱、散熱盤洞孔底部，以保證接觸良好，提高測試的準確性。但是不少學生忽略了這一點，在實際操作中經常出現熱電偶的硅脂涂抹部分裸露在兩盤洞孔外。將熱電偶搭在兩盤的邊緣模擬接觸不充分的實驗操作，實驗曲線如圖6所示。從圖6可見，熱電偶接觸不充分曲線和參考曲線位置比較接近，但曲線斜率偏差較大。從表1中的實驗數據可以看出，散熱盤的穩態溫度為45℃，但是導熱系數百分差為38.0%，偏差非常大。熱電偶與兩盤接觸不充分，導致測試靈敏度降低，測得的散熱盤溫度變化數據變緩，曲率(Δθ/Δt)|θ=θ2減小，計算出的導熱系數值偏低。

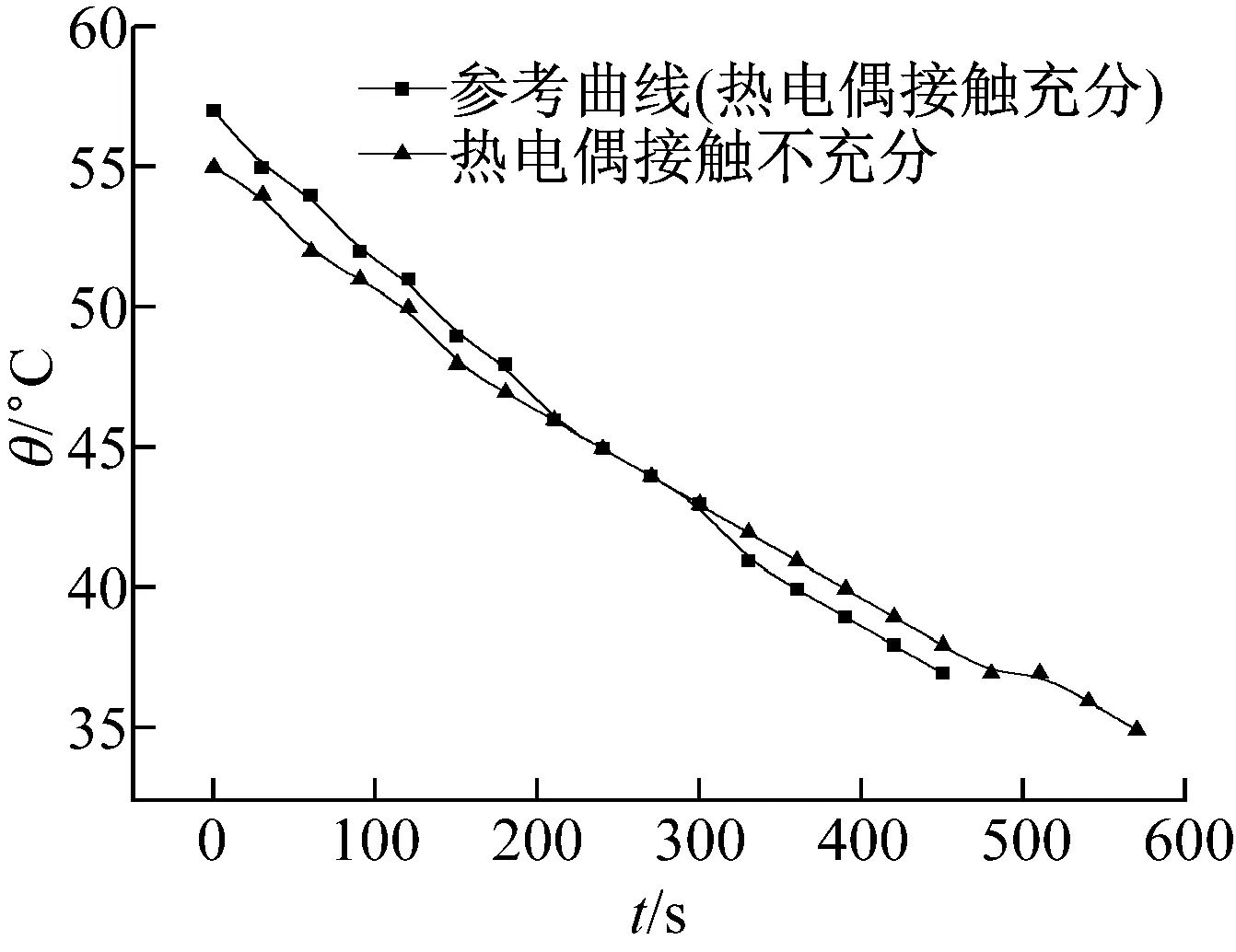
圖6 熱電偶與加熱、散熱盤接觸不充分對比實驗曲線

3 結 語

上述穩態法測量導熱系數的模擬誤操作實驗表明，誤操作影響散熱盤的穩態溫度和樣品的導熱系數。其中，樣品與兩盤未對齊10%時，散熱盤穩態溫度降低2℃，導熱系數減小6.7%；施加2 kg額外壓力時，散熱盤穩態溫度升高1℃，導熱系數增大2.2%；散熱盤穩態溫度降低3℃時，導熱系數減小35.8%；加熱過程未開風扇時，散熱盤穩態溫度升高11℃，導熱系數增大48.6%；熱電偶與兩盤接觸不充分時，散熱盤穩態溫度降低2℃，導熱系數減小38.7%。實驗中，誤操作對兩盤的溫差θ1-θ2和以及散熱盤穩態點處的曲率(Δθ/Δt)|θ=θ2影響較大。在未達到穩態時測試、熱電偶與兩盤接觸不充分的誤操作中，散熱盤穩態點處的曲率(Δθ/Δt)|θ=θ2大幅減小，導致導熱系數明顯減小；在加熱過程未開風扇的誤操作中，散熱盤的穩態溫度以及穩態點處的曲率(Δθ/Δt)|θ=θ2均有大幅增加，導致導熱系數明顯增大。

[1] 朱亞彬, 成正維, 劉依真. 對不良導體導熱系數測量實驗的改進[J]. 大學物理, 2004, 23(4): 25-27.

Zhu Ya-bin, Cheng Zheng-wei, Liu Yi-zhen. The improvement of the experiment for thermal conductivity of poor conductor[J]. College Physics, 2004, 23(4): 25-27.

[2] 楊永華, 曾 輝, 陳美華. 改進型導熱系數測量儀的研制與實驗[J]. 實驗室研究與探索, 2011, 30(3): 20-23.

Yang Yong-hua, Zeng Hui, Chen Mei-hua. Development and experiment of improved thermal conductivity measurement instrument

[J]. Research and Exploration in Laboratory , 2011, 30(3): 20-23.

[3] 孫慶龍, 王玉梅. 利用穩態法測定不良導體的導熱系數[J]. 計量與測試技術, 2010, 37(10): 69-70.

Sun Qing-long, Wang Yu-mei. Measuring the thermal conductivity of poor conductor by using the steady state method[J]. Metrology and Measurement Technique, 2010, 37(10): 69-70.

[4] 解俊梅, 田淑英, 侯方卓. 穩態圓筒法測定材料的導熱系數[J]. 實驗室研究與探索, 1997, 16(3): 42-45.

Xie Jun-mei, Tian Shu-ying. Measuring the thermal conductivity by using the steady cylinder method[J]. Laboratory Research and Exploration, 1997, 16(3): 42-45.

[5] 張建智, 周孑民, 章世斌. 穩態圓筒壁法自動測量顆粒導熱系數的改進[J]. 有色金屬, 2004, 56(4): 146-149.

Zhang Jian-zhi, Zhou Jie-min, Zhang Shi-bin. Improvement of particle thermal conductivity automatic measuring with steady cylinder method[J]. Nonferrous Metals, 2004, 56(4): 146-149.

[6] 周其云. 溶液導熱系數測定儀的研制[J]. 實驗室研究與探索, 1996, 15(3): 60-61.

Zhou Qi-yun. Development of the instrument for measuring the solution thermal conductivity[J]. Laboratory Research and Exploration, 1996, 15(3): 60-61.

[7] 李麗新, 劉圣春, 劉秋菊. 用綜合測量方法設計固體導熱系數測試實驗臺[J]. 實驗室研究與探索, 2006, 25(4): 435-438.

Li Li-xin, Liu Sheng-chun, Liu Qiu-ju. Design of thermal conductivity test desk for solid materials with multi-measuring method[J]. Research and Exploration in Laboratory, 2006, 25(4): 435-438.

[8] 賈斐霖, 李林, 史慶藩. 穩態法測算導熱系數的原理[J]. 材料科學與工程學報, 2011, 29(4): 609-613.

Jia Fei-lin, Li Lin, Shi Qing-fan. Principle of measuring thermal conductivity based on steady-state method[J]. Journal of Materials Science and Engineering, 2011, 29(4): 609-613.

[9] 馮毅, 梁滿兵. 穩態平板導熱系數測定儀的誤差分析[J]. 廣州化工, 2006, 34(1): 56-59.

Feng Yi, Liang Man-bing. Error analysis on the stable flat measuring instrument for thermal conductivity[J]. Guangzhou Chemical Industry, 2006, 34(1): 56-59.

[10] 李鋒, 鄧剛鋒. 基于LabVIEW的不良導體導熱系數測量系統[J]. 計算機測量與控制, 2009, 17(10): 1928-1930.

Li Feng, Deng Gang-feng. Measuring system of thermal conductivity of poor conductor based on LabVIEW[J]. Computer Measurement and Control, 2009, 17(10): 1928-1930.

[11] 楊世銘, 陶文栓. 傳熱學[M]. 北京: 高等教育出版社, 2000.

[12] 吳鐵山, 李道銀. 大學物理實驗[M]. 武漢: 湖北科學技術出版社, 2005.

[13] 徐福新, 劉碧蘭. 大學物理實驗[M]. 長沙: 中南大學出版社, 2011.

[14] 楊黨強, 吳綱, 金亞平. 大學物理實驗[M]. 北京: 中國電力出版社, 2009.

[15] 趙法剛, 王云霞. 保溫材料導熱系數的自動化測量[J]. 自動化與儀表, 2009, 24(1): 48-50.

Zhao Fa-gang, Wang Yun-xia. Thermal conductivity automatic measurement of insulated materials[J]. Automation and Instrumentation, 2009, 24(1): 48-50.