撓性航天器在軌分離沖擊緩沖模糊滑模控制研究①

趙剛練，姜 毅，陳余軍，劉 冬

(1．北京理工大學 宇航學院，北京 100081;2．中國空間技術研究院，北京 100094)

0 引言

隨著航天器的發展，空間伴飛、小衛星編隊等逐漸成為航天器發展的一個重要方向。有效載荷在軌分離是完成這些功能和任務的基礎。撓性航天器與有效載荷分離過程中，為保證有效載荷分離后具有一定的分離速度，分離機構必須提供足夠的分離推力推動有效載荷運動。近幾年國內對在軌分離過程進行了較多的研究［1－2］，但對于分離反作用力對航天器的影響及分離推力的緩沖并未進行深入分析。分離沖擊載荷具有時間短、頻帶寬和峰值大的特點，分離過程中航天器基座受到較大的沖擊，而且瞬間過載可能造成航天器中的精密設備損壞。因此，需要采用緩沖裝置降低傳遞到基座的沖擊載荷峰值。

有效載荷分離時間量級在150 ms左右，傳統的彈簧阻尼機構響應速度慢，難以根據沖擊載荷的變化實時調整。近年來，隨著材料科學的發展，智能材料被廣泛用于減振控制。其中，磁流變阻尼器具有可控、連續和響應快速的特點［3］，在沖擊減振領域已經得到較為廣泛的應用［4－5］。為了保證平穩的緩沖，需要對緩沖裝置實施主動控制。滑模控制具有設計靈活、控制精度高、對外部擾動和參數不確定性不敏感等特點，從而成為非線性控制的一種重要控制方法，并應用于沖擊減振領域［6－7］。然而，滑模控制由于采用不連續切換控制項使系統存在抖振現象，這種抖振可能會使系統不穩定。使用連續函數代替切換函數［8－9］與邊界層調整技術［10］能夠有效抑制抖振現象。此外，國內外學者將滑模控制與模糊控制相結合，也有效抑制了抖振，并提高了系統的控制品質，但均未考慮誤差變化速率的影響［11－12］。

基于以上研究，本文提出將磁流變阻尼器用于航天器沖擊減振，給出了磁流變阻尼緩沖器的基本結構和動力學模型，建立了大范圍運動撓性航天器的動力學模型，在傳統模糊指數趨近律［13］基礎上結合二維模糊控制，提出了以誤差和誤差導數作為模糊輸入，指數趨近律系數為模糊對象的控制策略。仿真結果證實了航天器平臺采用磁流變阻尼緩沖器減振的有效性和此控制策略良好的跟蹤特性。

1 含緩沖裝置撓性航天器動力學模型

1．1 磁流變阻尼緩沖器結構與動力學模型

單桿磁流變阻尼緩沖器結構見圖1，主要包括活塞桿、活塞、缸筒、磁流變液、線圈和氣囊。活塞與缸筒間的環形面積形成間隙，兩者相對運動使磁流變液體從該間隙流過。線圈與活塞和缸筒一起構成磁路，使流液間隙中產生磁場，當液體通過流液間隙時，受到磁場作用，產生屈服應力。

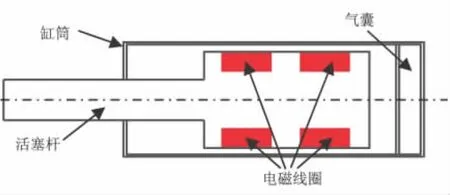
圖1 磁流變阻尼緩沖器結構圖Fig．1 Configuration of MR shock absorber

為了簡化計算和便于控制，選擇Bingham模型對緩沖器進行建模。在沖擊載荷作用下，環形阻尼通道內磁流變液的速度和加速度值可能很大，使磁流體的流動狀態為不規則流動(湍流)，必須考慮慣性力的作用。根據流體力學分析可知，磁流變阻尼緩沖器總阻尼力［14］為

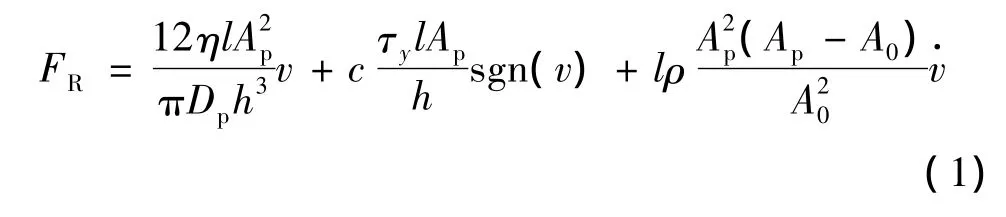
式中 第一項為粘滯阻尼力;第二項為庫倫力，即可控制力;第三項為慣性力;η為磁流變阻尼液的表現粘度;l為阻尼器的有效長度;Ap為活塞有效面積;h為環形間隙大小;Dp為缸筒內直徑;ρ為磁流變液的密度;c為給定流量條件下的常數，取值為2～3之間。

1．2 含緩沖裝置的撓性航天器動力學模型

典型飄浮基撓性航天器系統由中心基座和撓性附件組成，對飄浮基航天器進行如下假設:

(1)兩側撓性附件可作為等截面小變形梁處理;

(2)執行分離任務過程中撓性附件與中心剛體處于鎖定狀態，即撓性附件與基座采用固定連接;

(3)不對基座的位姿進行主動控制，忽略微重力、鎖定機構的柔性和摩擦;

(4)緩沖裝置和有效載荷都嵌入基座，且與基座是移動關系，有效載荷分離后解除與基座的移動約束。

撓性航天器模型如圖2所示，航天器基座和緩沖裝置的活塞缸統稱為B1，B2和B3為撓性附件，B4為緩沖裝置的活塞桿，B5為有效載荷。

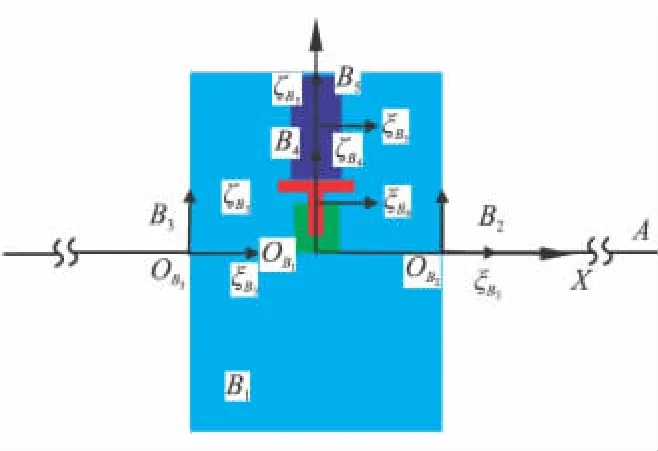
圖2 飄浮基撓性航天器動力學模型Fig．2 Dynamic model of free-floating flexible spacecraft

建立圖 2 所示的全局慣性坐標系 XYZ，ξB2ηB2ζB2和ξB3ηB3ζB3為撓性體 B2和 B3的動坐標系;ξB4ηB4ζB4、ξB5ηB5ζB5為位于B4、B5質心的隨體坐標系，基座的隨體坐標系位于基座質心且初始時刻與全局慣性坐標系重合。

撓性附件的廣義坐標為

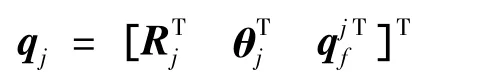
式中 Ri、Rj分別是隨體系原點、動坐標系原點的全局位置矢量;θi、θj分別是隨體系、動坐標系的歐拉轉角;是廣義彈性坐標。

RB1、RB4分別表示基座、活塞桿的質心 OB1、OB4的全局位置矢量，RB2、RB3分別表示B2和B3動坐標系原點的全局位置矢量，則基座上的任一點P和撓性體B2的任一點Q在全局坐標系中的位置矢量為

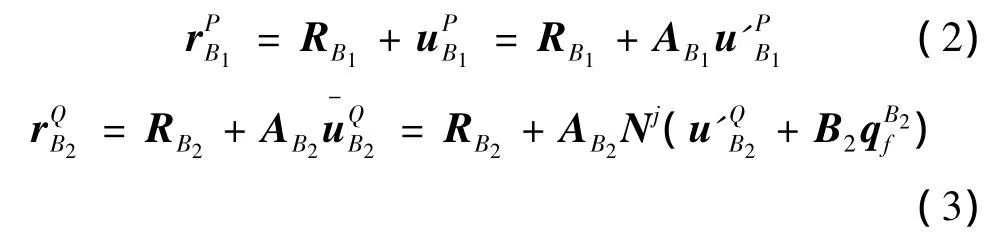
式中 AB1為B1隨體坐標系與全局坐標系的坐標變換矩陣;AB2為B2動坐標系與全局坐標系的坐標變換矩陣;為P點在隨體坐標系ζB1ηB1ζB1中的坐標列陣;和分別為Q點未變形前和變形后在動坐標系ηB2ζB2中的坐標列陣為 B2上第 j個單元在動坐標系中的單元形函數;Cj為單元局部坐標系向物體動坐標系的變換矩陣;為單元結點位移向量局部坐標與動坐標系之間的變換矩陣;為常數矩陣;Φj為單元局部坐標系中的單元形函數，本文采用三維二節點歐拉-伯努利梁單元進行離散。

同理，可得其他體上任一點的位置矢量。

對各個組件的矢量坐標求導，可得系統的總動能和彈性勢能如下:

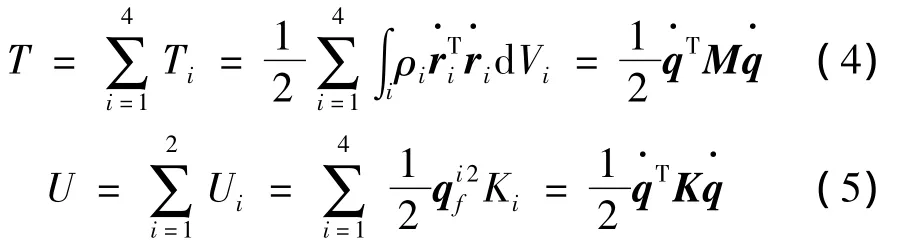
矩陣M為

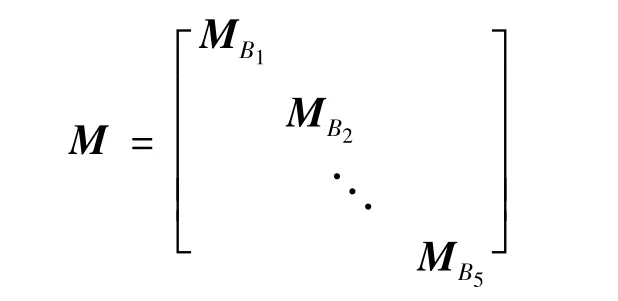
其中，柔性體B2和B3采用一致協調質量矩陣計算:

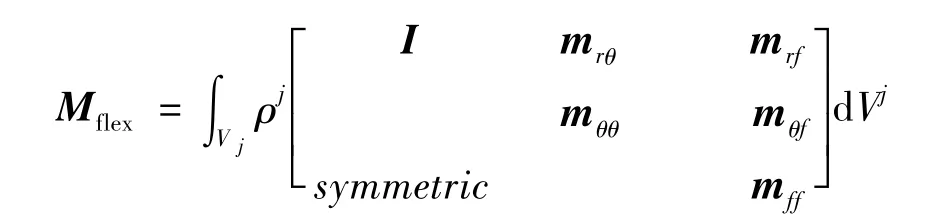
對于剛體B1、B4和B5的質量矩陣可由下式求解:

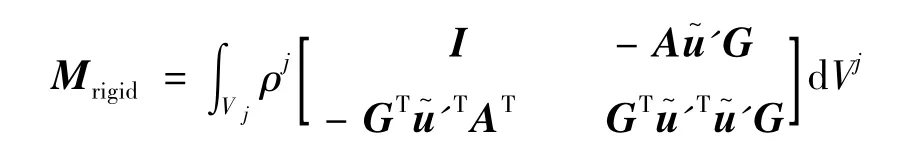
其中

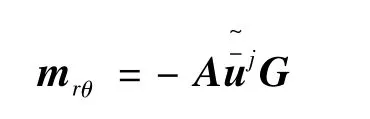
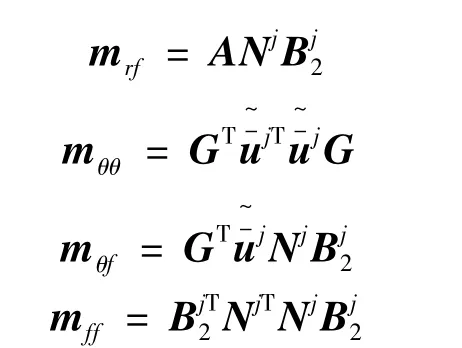
式中 G的各列分別為沿3個歐拉轉動軸的單位矢量在全局坐標系中的坐標列陣［15］。

利用式(4)和式(5)由拉格朗日方程可得漂浮基撓性航天器系統剛柔耦合多體動力學方程:

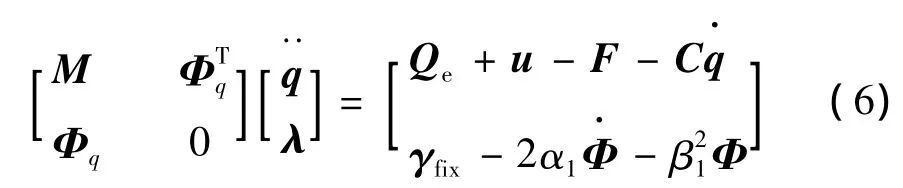
式中 q為系統的廣義坐標;Φ為系統約束方程;Φq為系統約束方程對廣義坐標的雅克比矩陣;λ為拉格朗日乘子;u為系統的廣義控制力;Qe為系統的廣義慣性力;F=Kq為系統的廣義彈性力;C=α2M+β2K為系統的阻尼;γfix為約束方程的右端項;α1、α2、β1、β2為常數。

令:

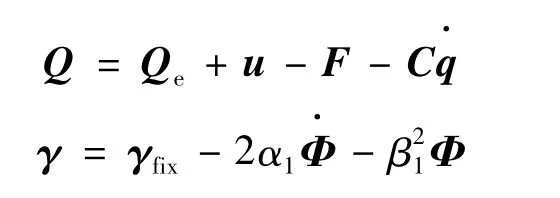
則

其中

由式(7)可得

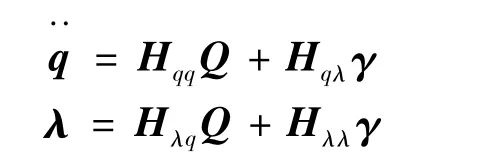
故此撓性航天器系統的狀態方程為

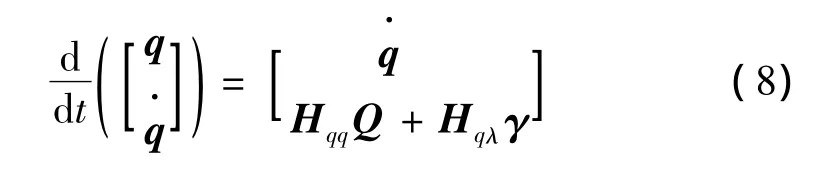
2 分離沖擊載荷下緩沖器控制策略

2．1 滑模控制設計與穩定性分析

為了降低沖擊載荷對安裝在基座中儀器的影響，采用緩沖裝置將短時大峰值的沖擊載荷轉換為長時小峰值的作用力。因此，需要控制磁流變阻尼緩沖器的庫倫力，保證緩沖裝置的總輸出阻尼力為恒定目標值，從而實現作用在基座上的力不隨沖擊載荷改變。根據此要求，將緩沖器的輸出與預期輸出值之間的差值e作為誤差控制。基于滑模控制的基本思想，選擇滑模面

其中，k的選擇滿足Hurwitz多項式條件。

為方便計算，采用高為炳教授提出的趨近律概念，選擇指數趨近律進行計算:

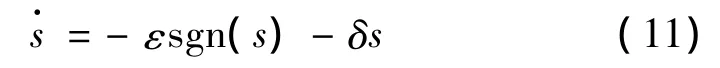
式中 ε和δ為調整趨近律的參數。

對式(9)求導得

由于航天器受到沖擊后基座和緩沖裝置同時運動，故式(12)中的位移、速度和加速度是緩沖裝置相對于基座隨體坐標系的值，則沿基座ζ方向的速度vζ和加速度aζ分別為

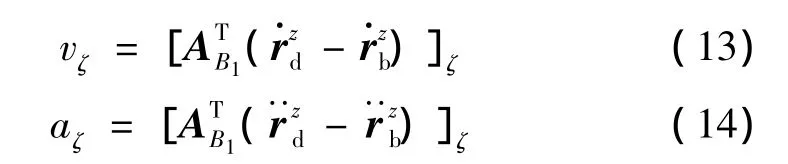
將式(1)、式(9)、式(10)、式(13)和式(14)代入式(11)，則有

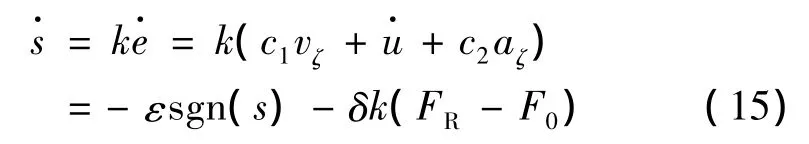
對式(15)進行化簡得

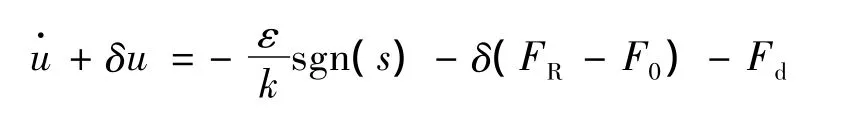
式中 Fd=(c1vζ+c2aζ)。

求解此微分方程并忽略與時間相關的冪次項，得控制力的表達式為

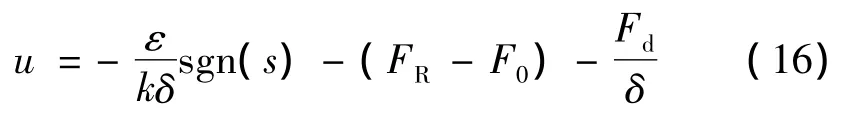
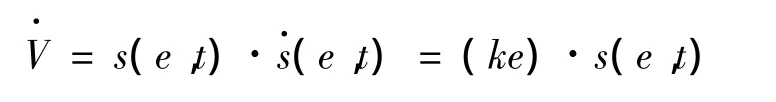
2．2 二維模糊滑模控制

控制律式(16)中的切換項用于補償建模誤差和外界干擾等不確定項，保證滑模存在性條件得到滿足，但也是造成抖振的主要原因。δs項影響系統趨近過程，從而影響系統的動態品質。為抑制抖振現象，本文提出以規范化的誤差和誤差的導數作為輸入的二維模糊規則來控制趨近律參數和的值和分別ε和δ是規范化后的值。將引入模糊控制后能夠考慮誤差導數變化對系統的影響，使控制系統根據誤差e的變化方向和當前誤差的正負及時調整輸出，從而提高系統對理想輸出的跟蹤效果，克服了傳統只通過e的正負控制輸出無法提前判斷誤差方向的缺點［16－17］。根據ε和δ對系統狀態的影響［18］，模糊控制規則設計原則為:

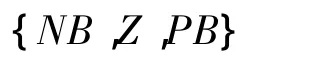
式中 NB為負大值;Z為零;PB為正大值。

為方便實時計算，采用三角形隸屬度函數，如圖3所示，模糊規則如表1所示。

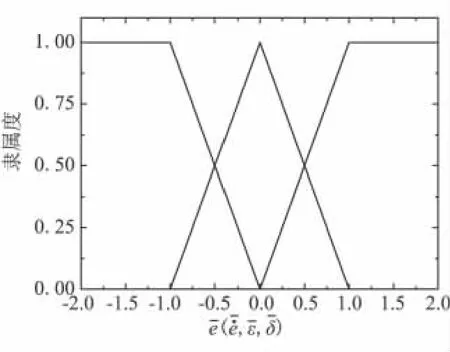
圖3 隸屬度函數Fig．3 Membership function

表 1 、控制規則Table 1 Fuzzy control rulesand

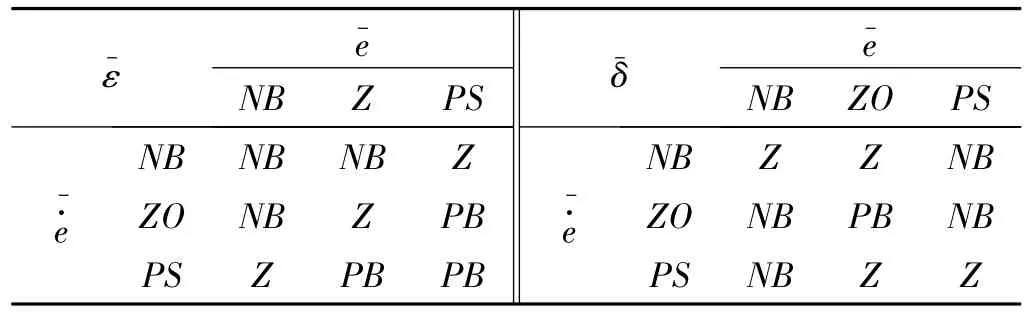
表 1 、控制規則Table 1 Fuzzy control rulesand

ε－ e －δ－ e －NB Z PS NB ZO PS e·－NB NB NB Z ZO NB Z PB e·－NB Z Z NB ZO NB PB NB PS Z PB PB PS NB Z Z

根據控制規則并采用代數積-Max-重心法［19］，將模糊控制器輸出量和轉化為精確的控制量。

采用模糊推理后控制量u的表達式為

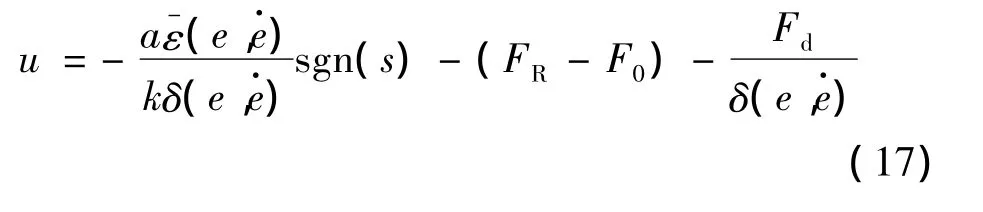
3 數值算例

飄浮基航天器處于無重力環境下，初始時刻系統處于靜止狀態。系統各組件的參數如表2和表3所示。撓性附件各劃分為6個梁單元，截面為20 mm×20 mm的正方形。緩沖裝置參數如下:ρ=3．09×103kg/m3、η =240 cP、l=350 mm、Ap=204 mm2、h=2 mm、Dp=8 mm，分離推力通過火工品燃燒產生高壓氣體作用于活塞產生，有效載荷所受推力如圖4所示。設仿真時間為5 s，仿真步長為1．0×10－5s，理想輸出 F0=90 N。經多次試探仿真，取 ε =0．05、δ=1 000、k=10對比緩沖裝置開啟(采用式(17)控制總阻尼力輸出)和緩沖裝置關閉(緩沖裝置與基座相對固定無阻尼力輸出)2種情況，仿真結果如圖5～圖9所示。

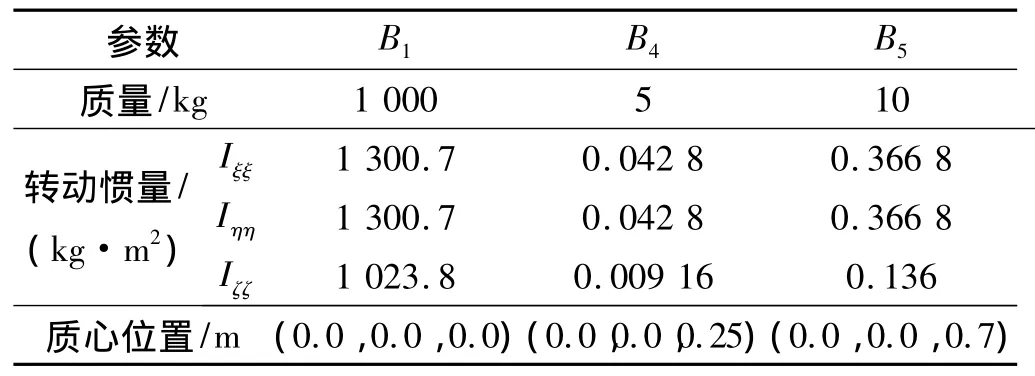
表2 基座和緩沖裝置物理參數Table 2 Physical parameters of the base and shock absorber

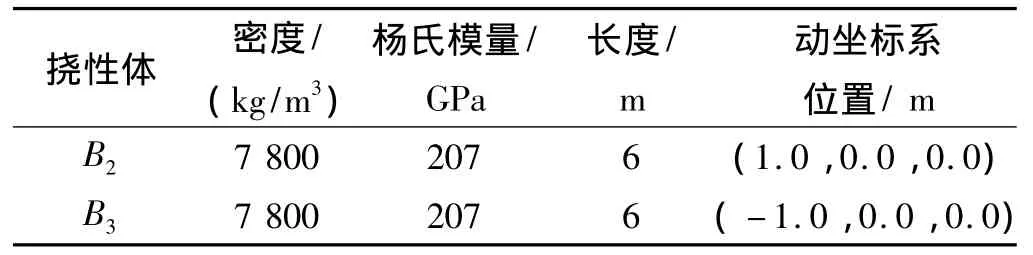
表3 撓性附件的物理參數Table 3 Physical parameters of flexible appendages

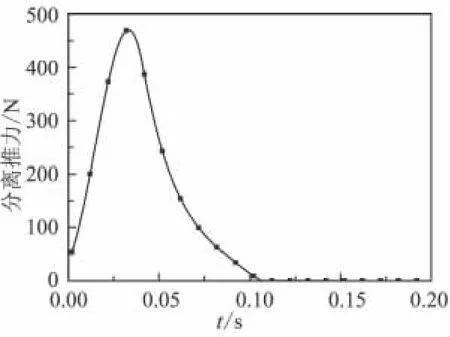
圖4 分離推力曲線Fig．4 Thrust curve

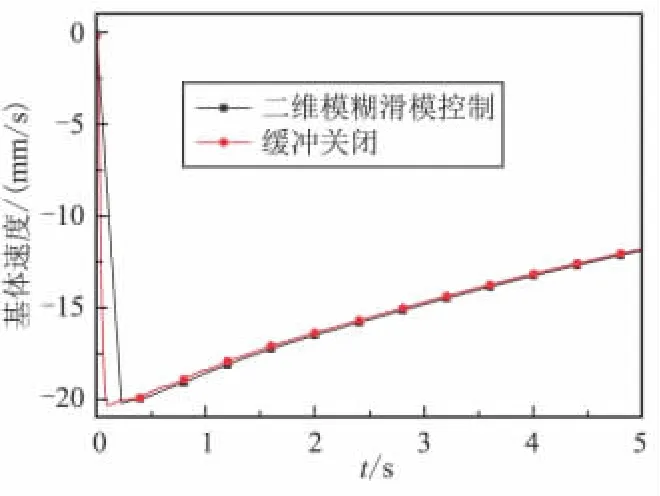
圖5 基體速度Fig．5 Velocity of the base

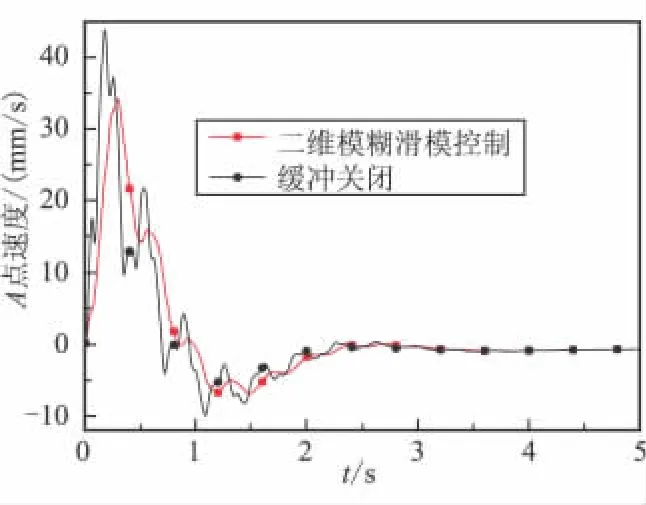
圖6 撓性體B2端點A相對于基體的速度Fig．6 Velocity of point A with respect to the base

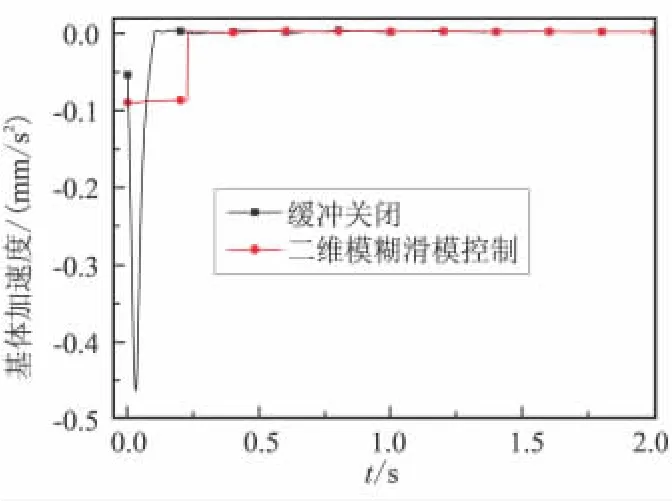
圖7 基體加速度Fig．7 Acceleration of the base

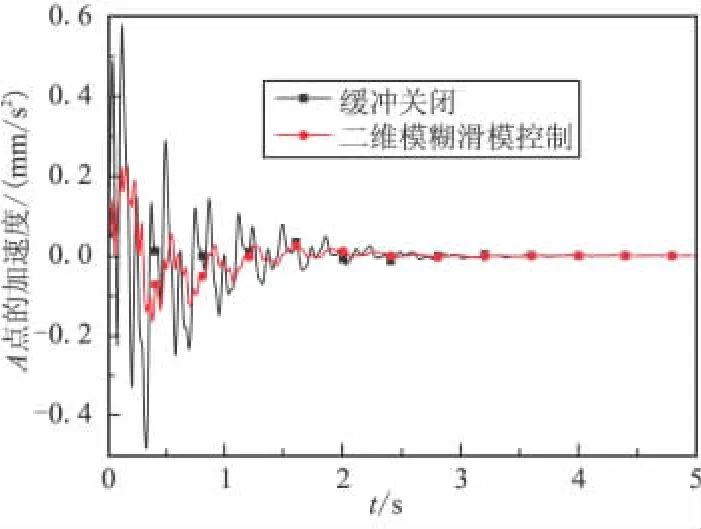
圖8 撓性體B2端點A相對于基體的加速度Fig．8 Acceleration of point A relative to the base

由圖5可知，緩沖裝置關閉時相對于減振裝置開啟時基座速度迅速上升，而且有波動，增加緩沖裝置后，基體最大速度由 20．35 mm/s降為 20．23 mm/s，到達最大速度后，由于撓性附件變形回彈基體逐漸減速。從圖6可看出，緩沖裝置輸出阻尼力時，端點A彈性變形速度曲線顯著平穩，波動頻率更低，而且峰值由43．81 mm/s下降為37．19 mm/s，下降幅度達到15．1%。

從圖7基體的加速度曲線可發現，采用緩沖裝置后，基體的加速度峰值顯著減小，由463．99 mm/s2降為90．87 mm/s2，降幅達到 80．4%，緩沖效果較為明顯。圖8為端點A相對于基體的加速度，與速度曲線類似，加速度峰值顯著下降，而且曲線波動減少，更為平穩。

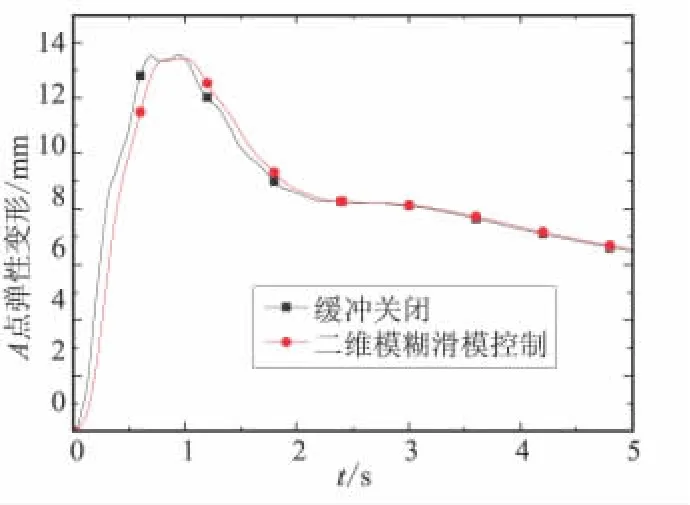
圖9 撓性體B2端點A的彈性變形Fig．9 Elastic deformation of point A in B2

從圖9中端點A相對于基座ζB1軸的彈性變形可看出，緩沖裝置關閉時在0．6～1 s內彈性變形曲線發生了局部波動，這是基座的剛性位移與撓性附件的彈性變形發生了強烈耦合所導致的。緩沖裝置輸出阻尼力后，彈性變形曲線變化較為平穩，最大彈性變形量由13．567 mm降為13．427 mm。另外可看出，由于分離時間短，且撓性附件振動頻率低。所以，緩沖裝置對撓性附件彈性變形的抑制作用不明顯。

為了說明本文控制方法的有效性，分別采用傳統滑模控制、單變量模糊滑模控制和本文的模糊滑模控制3種方法，對緩沖裝置進行控制，并進行仿真計算，仿真結果如圖10、圖11所示。

從圖10所示的緩沖裝置相對于基座的滑動距離曲線可看出，本文控制方法的滑動距離為0．313 2 m，此距離相對于基座的尺寸在接受范圍之內，滿足工程要求。從局部放大圖也可看出，穩定輸出后，采用二維模糊滑模控制的緩沖裝置滑動距離小于傳統滑模控制和單變量模糊滑模控制的滑動距離。這是由于磁流變阻尼緩沖器中的粘滯阻尼項和慣性力項與相對速度和加速度相關。

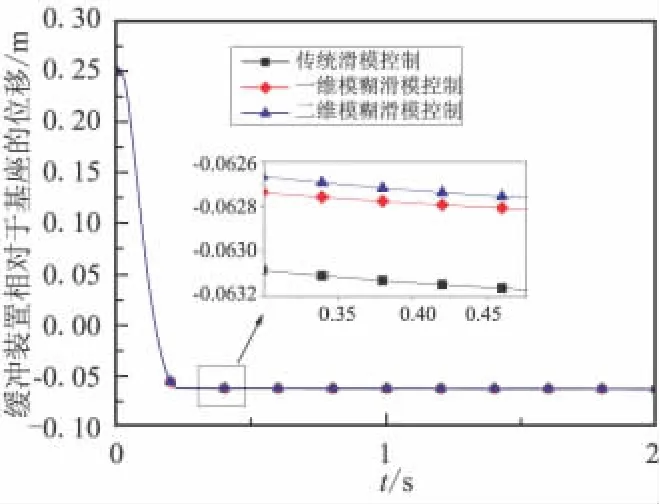
圖10 緩沖裝置相對于基座的位移Fig．10 Displacement of the shocker absorber relative to the base

3種控制策略下緩沖器輸出的總阻尼力如圖11所示，總阻尼力峰值分別為 92．51、92．14、91．78 N，超調量分別為 2．79%、2．38%、1．98%。從圖 11 可知，傳統滑模控制抖振嚴重，采用本文控制策略后，抖振現象得到了抑制，而且阻尼力的峰值小于另外2種控制方法，且穩定輸出值為90．03 N比單變量模糊的穩定值89．95 N更接近理想值90 N。以上兩點說明了本文控制方法在跟蹤理想輸出和穩定值與理想值接近程度兩方面的有效性。

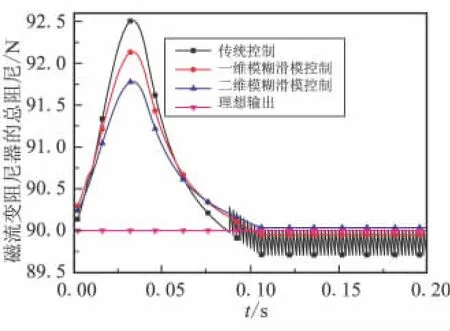
圖11 磁流變阻尼器的總阻尼力Fig．11 Damping force of MR damper

4 結論

(1)本文將磁流變阻尼器用于航天器沖擊減振，采用有限元與Lagrange方法，建立了含減振裝置的飄浮基撓性航天器的剛柔耦合多體動力學模型，并開發了相應的計算程序。基于此模型，針對指數趨近律滑模控制，提出了將誤差和誤差導數作為輸入的模糊控制方法，有效降低了分離推力對航天器的沖擊。

(2)數值計算結果表明了磁流變緩沖裝置對航天器緩沖的有效性。其中，緩沖裝置顯著降低了基座所受的沖擊，而且降低了基座與撓性附件的耦合作用，使附件的速度和加速度變化更為平穩。

(3)與傳統趨近律滑模控制方法和一維模糊滑模控制方法進行了仿真對比。結果表明，本文提出的控制方法提高了系統的動態品質，并有效抑制了系統的抖振。

［1］ 舒燕，李志．在軌釋放、分離載荷動力學仿真研究［J］．航天器環境工程，2012(1):18-22．

［2］ 沈曉鳳，肖余之，康志宇．小衛星偏心分離動力學仿真模型的建立與驗證［J］．飛行力學，2012(3):258-262．

［3］ Weiss K，Duclos T，Carlson J，et al．High strength magnetoand electro-rheological fluids［J］．Society of Automotive Engineers，932451，1993．

［4］ 張志勇，劉鑫，黃彩霞，等．具有參數不確定性的車輛座椅懸架輸出反饋半主動控制［J］．振動與沖擊，2013(14):93-97，147．

［5］ 涂奉臣，張洋，陳照波，等．采用磁流變阻尼器的整星隔振平臺試驗研究［J］．振動與沖擊，2012(21):33-36，40．

［6］ 李趙春，王炅．火炮磁流變阻尼器試驗分析與動態模型［J］．振動與沖擊，2012(1):64-67．

［7］ 張步云，陳懷海，賀旭東，等．磁流變阻尼器減振特性實驗研究［J］．南京航空航天大學學報，2012(6):855-861．

［8］ Chung J C Y，LIN C L．A transformed Lure problem for sliding mode control and chattering reduction［J］．IEEE Transactions on Automatic Control，1999，44(3):563-568．

［9］ Kuo T C，Huang Y J，Chang S H．Sliding mode control with self-tuning law for uncertain nonlinear systems［J］．Isa Transactions，2008，47(2):171-178．

［10］ Erbatur K，Kawamura A．Chattering elimination via fuzzy boundary layer tuning［M］．Iecon-2002，Proceedings of the 2002 28th Annual Conference of the Ieee Industrial Electronics Society，2002(1-4):2131-2136．

［11］ Wang J，Rad A B，Chan P T．Indirect adaptive fuzzy sliding mode control，Part I，fuzzy switching［J］．Fuzzy Sets and Systems，2001，122(1):21-30．

［12］ Wang S Y，Hong C M，Liu C C，et al．Design of a static reactive power compensator using fuzzy sliding mode control［J］．International Journal of Control，1996，63(2):393-413．

［13］ Gao W，Hung J C．Variable structure control of nonlinear systems，a new approach［J］．Industrial Electronics，IEEE Transactions on，1993，40(1):45-55．

［14］ 朱超．沖擊載荷下磁流變阻尼器設計優化與控制算法研究［D］．南京理工大學，2012．

［15］ Shabana A A．Dynamics of multibody system［J］．New York，Cambridge University Press，2005．

［16］ 張永生，趙淑琴．船用蒸汽發生器水位的模糊自適應PID控制［J］．中國艦船研究，2013，8(3):106-109．

［17］ Rojas-Ramírez E，Benítez-Read JS，Segovia-De-Los Ríos A．A stable adaptive fuzzy control scheme for tracking an optimal power profile in a research nuclear reactor［J］．Annals of Nuclear Energy，2013，58:238-245．

［18］ Kun Jiang，Zhang Jing-gang，Chen Zhi-mei．A new approach for the sliding mode control based on fuzzy reaching law［A］．Proceedings of the 4th World Congress on the Intelligent Control and Automation，2002(1):656-660．

［19］ Kandel A，Langholz G．Fuzzy control systems［M］．Florida，CRC Press Inc，1994．