基于逆最優問題的最優制導律及特性分析①

王 輝，王 江，郭 濤，王廣帥

(1．北京理工大學宇航學院，北京 100081;2．北京航天自動控制研究所，北京 100854)

0 引言

隨著智能彈藥及精確制導技術的快速發展，很多攻擊任務不僅要求精確命中，還對彈道末段的速度矢量角、攻角等提出了附加約束，如對裝甲目標的越頂攻擊、對堅固掩體內目標的侵徹攻擊等，這均對精確導引技術提出了新的要求。

實際上，根據不同的任務需求，相關學者一直在研究各種具有針對性的制導律，并不斷探索新的制導律。其中，能量最優制導律吸引的關注最多，工程應用也最廣泛［1－3］。比例導引和彈道成型可認為是能量最優制導律的典型代表，相關研究也最深入［1－6］。比例導引的種類較多，如經典比例導引、增強型比例導引［1－3］、分段式比例導引［7－8］等。彈道成型制導律的概念最早由Zarchan提出［1］，其提出的制導律也被稱為經典彈道成型制導律。在Zarchan工作基礎上，Ben-Asher，Yaesh，Ryoo等對彈道成型的制導特性、剩余飛行時間(time-to-go)估算方法等進行了深入研究［5－6，9－10］。傳統的能量最優制導律大都基于線性二次型最優控制理論，以控制量的平方的積分最小為目標函數，權函數取為常值1［1－2］。2006 年，Ryoo 和 Ohlmeyer等在研究角度控制問題時，引入導彈剩余飛行時間的冪函數，實現了彈道成型制導律的擴展，拓展了與此相關的制導律的研究范圍［4－5，10］。

本文在典型的能量最優制導律基礎上，創新性地將制導律的2個特征根從有限的點/線擴展到幾乎所有的正實根，提出了制導律的逆最優問題，闡述了逆最優制導律中性能指標加權矩陣的構造、求解過程，并對不同特征根下的逆最優制導律的制導特性進行了系統研究。

1 能量最優制導律的常規形式

對地面靜止或慢速移動目標，導彈和目標的幾何關系如圖1所示，OXY表示地面坐標系，M0表示導彈初始位置，LOS表示當前彈目視線(line of sight)，LOS0表示初始彈目視線，LOSf表示終端攻擊時刻的彈目連線，(xt，yt)表示目標位置。圖1中主要符號定義如表1所示，所有的角度定義逆時針為正，順時針為負。

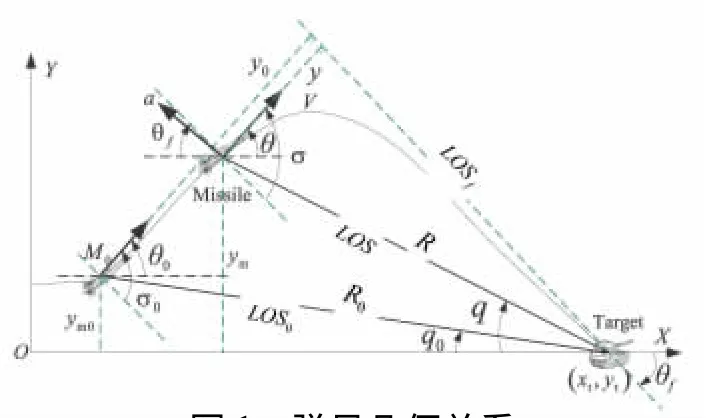
圖1 彈目幾何關系Fig．1 Geometry of the missile and target

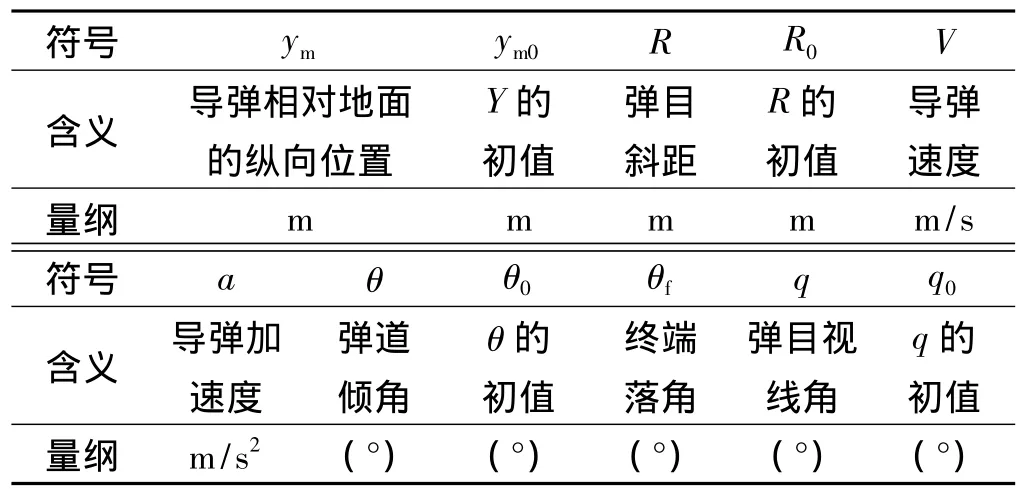
表1 主要符號定義Table 1 Definition of the main symbols

為便于后續的表述和推導，定義相對于終端彈目連線的縱向位置y和速度矢量角σ，初值分別為y0、σ0。由定義可知，σ、θ、θf的關系為

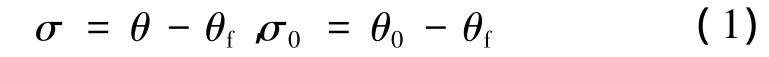
縱向位置 Y、y 與 θf、q 的關系為

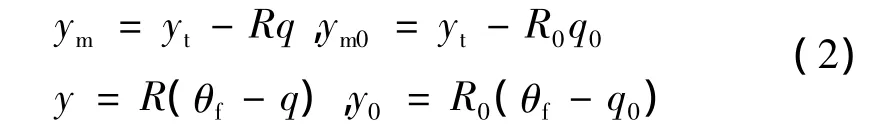
根據圖1所示的彈目幾何關系，建立如下的運動方程:

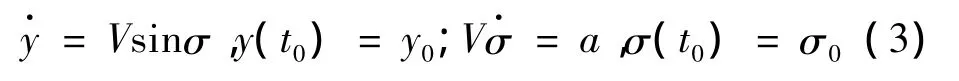
當忽略駕駛儀動力學時，導彈的加速度指令等于加速度響應，即u(t)=a，u為控制量。為了對式(3)進行線性化，假設V是常值、σ為小角，這也是研究線性最優制導律的2個常用假設［1－2］。這樣，經線性化后，式(3)可表示為

其中，v=Vσ表示垂直于終端彈目連線的速度分量。

將式(4)寫成矩陣的形式:

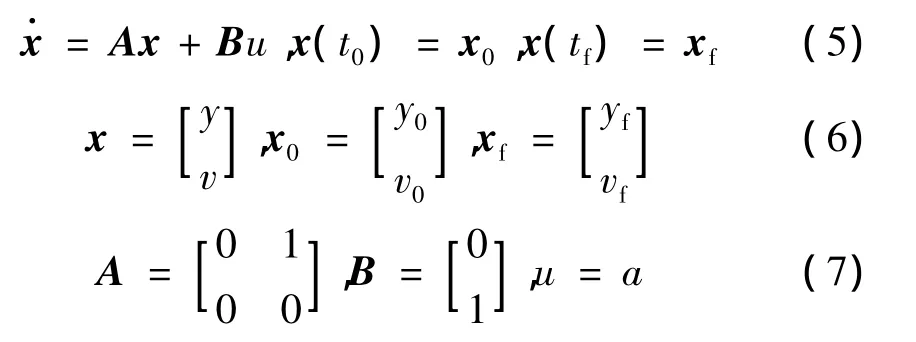
式中 tf為導彈制導時間;x0為狀態初值;xf為狀態終值。

根據式(5)～式(7)和最優控制理論，設定不同形式的權函數和目標函數，在不同的終端狀態約束下，則可得到不同的能量最優制導律。如僅約束終端位置yf=0，不考慮終端約束權函數和狀態權函數，控制權函數 R設為1，則得到傳統的比例導引制導律(CPNGL，classic proportional navigation guidance law)，權函數R設為1/(tf－t)n，n≥0，則得到擴展的比例導引律(EPNGL，extended proportional navigation guidance law);若同時約束yf=0，vf=0，則可分別得到傳統的/擴展的帶落角約束的最優制導律(COGLIAC/EOGLIAC，classic optimal guidance law with impact angle constraint/extended optimal guidance law with impact angle constraint)。

表 2 給出了幾種典型的能量最優制導律［1－2，4－5］。表2中，tgo=tf－t，表示導彈剩余飛行時間。對表2中帶落角約束的制導律，由于文中定義了相對于終端彈目連線的角度σ，終端角度約束θf隱式包含于制導律中;若將式(1)及線性化的式(2)帶入制導律中，則制導律可變換為直接含有終端角度約束θf的常規形式［1，4－6］。

2 逆最優制導律的提出及其加權矩陣的構造

2．1 最優制導律的擴展及其逆最優問題

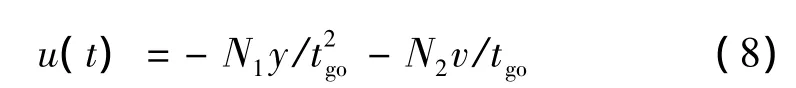
表示成矩陣的形式:

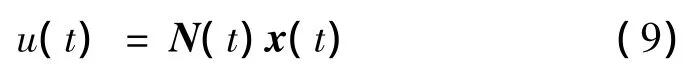
其中，N(t)為線性時變的制導增益矩陣，即

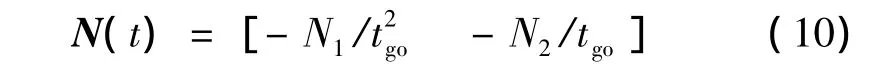
表2 典型的能量最優制導律Table 2 Typical energy optimal guidance laws

進一步，將式(8)表示成相對于地面坐標系的微分方程形式，有

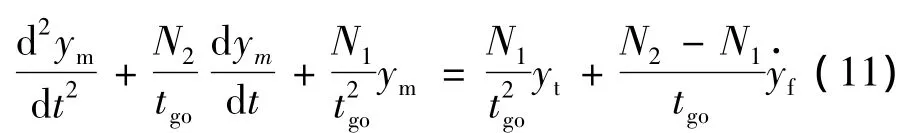
由式(11)可看出，制導律是否含有終端角度約束取決于N1、N2取值，當N1=N2時(如PN)，則制導律自然地不包含終端角度約束。

令y=tgoλ，則式(8)可寫為 λ2－(N2+1)λ +N1=1，不妨再令方程的兩實根分別為 λ1、λ2(λ1＞ λ2)，則N1=λ1λ2，N2=λ1+λ2－1，此時式(8)又可表示成:

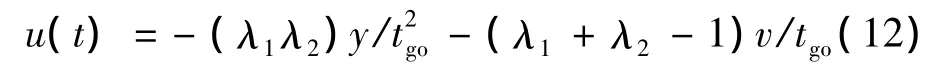
因 N1＞0，N2＞0，故 λ1λ2＞0，λ1+λ2－1 ＞ 0，即λ1＞0，λ2＞0，λ1+λ2＞1。根據表1中導航系數，容易得到典型最優制導律特征根(Characteristic roots，CR)λ1、λ2間的對應關系，如圖2所示，其中陰影區表示逆最優制導律可能的特征根區域。

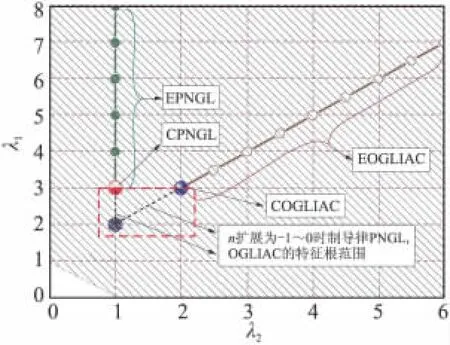
圖2 典型最優制導律的特征根Fig．2 CR of the typical energy optimal guidance laws

在圖2中，前述幾種典型最優制導律的特征根只占據了有限的點/線區域，而提出的逆最優制導律極大地擴展了可能的特征根范圍。現在的重點是能否找到合適的目標函數J，使最優制導律的形式滿足式(9)，這就是最優制導律中的逆最優問題［10］。相應的，式(8)或式(12)稱為逆最優制導律。

2．2 逆最優制導問題中加權矩陣的構造

為便于推導，將式(5)的狀態方程和式(9)的控制方程統一寫成如下形式:

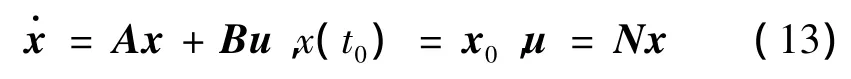
式中 x為m×1維向量;u為控制量，由式(5)的標量擴展為n×1維向量。

目標函數J設為

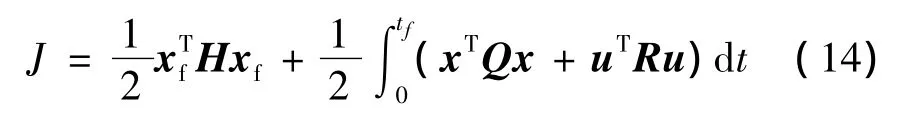
式中 H為終端約束權矩陣;Q為狀態權矩陣;R為控制權矩陣;H、Q、R均為對稱矩陣。

對由方程(13)構成的線性閉環制導系統，逆最優問題就是找到矩陣A、B、N所需滿足的充分必要條件，確定矩陣H、Q和R并使式(14)的性能指標最小［10－11］。

對式(13)所示的最優控制問題，其直接的最優解N可由Riccati微分方程得到，即

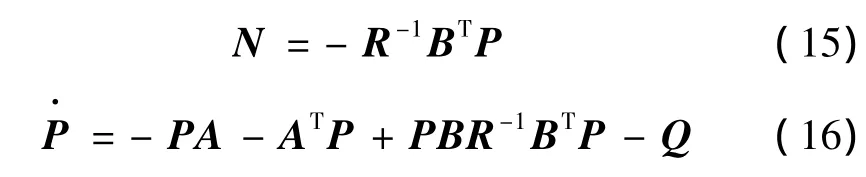
式中 P為對稱矩陣。

式(16)的邊界條件為

為了使方程(16)的解P(t)存在并唯一，傳統的結論是要求H≥0，Q≥0，R ＞0，但文獻［10－11］指出，對方程(13)～(14)所示的系統，當滿足一定條件時，Q≥0并不是必需的。

不加證明，給出定理1:對方程(13)所示的線性閉環系統，矩陣B、N在區間［t0，tf］上可微并具有確定的常量秩，則可構造如式(14)所示的性能指標函數，其中矩陣H、Q、R滿足如下條件:

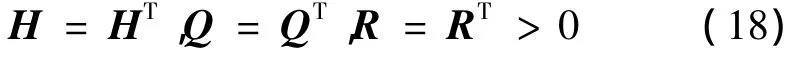
對區間［t0，tf］上的任意時間t及任意初值x0，如果矩陣NB具有n個線性獨立的實特征向量且所有的特征向量均非正，且矩陣B、N的秩滿足:

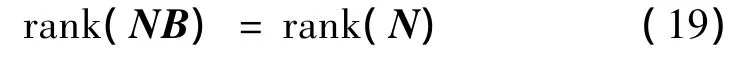
則能保證性能指標J的最小值J*≥0;

若矩陣B、N的秩滿足式(20):

則能保證J*＞0。

假設定理1條件都滿足，則可構造性能指標函數J的具體形式。首先構造矩陣R=RT＞0使矩陣RNB是對稱的。已經知道矩陣NB的特征向量是線性獨立的實向量，設矩陣V的列由BTNT的特征向量組成，則有如下表達式:

式中 U為BTNT特征值構成的對角陣。

這樣，有定理2:假設矩陣NB具有n個線性獨立的實特征向量，對由式(22)給定的實矩陣R=RT＞0可使矩陣RNB是對稱的，即

其中，矩陣V的列選自矩陣BTNT的特征向量。

下面根據式(15)的結果來求解對稱矩陣P:

設W為滿足下列等式的任意n×m實矩陣，則

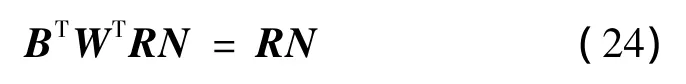
對比式(23)和式(24)可看出，－WTRN是式(23)中關于P的解，但－WTRN并不能保證P是對稱的。為了得到對稱的解，令

在式(25)兩邊同時左乘BT，得到

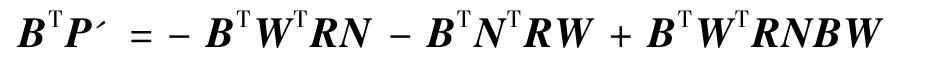
根據式(24)的結論，上式可簡寫為

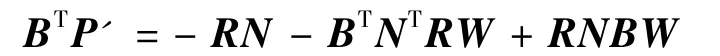
又由于矩陣R=RT，(RNB)T=BTNTR=RNB，則上式可進一步簡化為

假設P是式(23)的任意實對稱矩陣解，聯立式(23)和式(26)，有

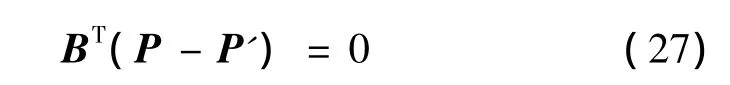
據此，可得式(15)的實對稱矩陣解P:

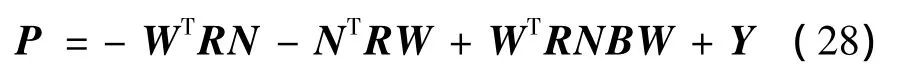
其中，Y為任意的實矩陣，滿足如下條件

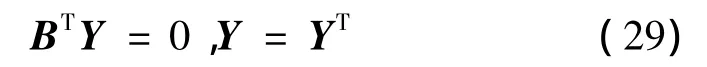
當矩陣NB的秩滿足式(19)的條件時，關于矩陣P有定理3:令矩陣R是實對稱的正定矩陣，RNB是對稱矩陣，如果rank(NB)=rank(N)，則滿足式(23)的實對稱矩陣P可由給定的矩陣R表示:

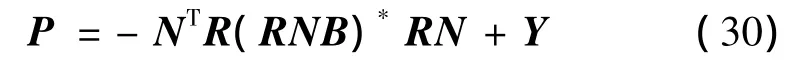
其中，矩陣Y滿足式(29)，符號*表示矩陣的Moore-Penrose廣義逆。

此外，矩陣H由H=P(tf)得到，矩陣Q由式(31)得到:

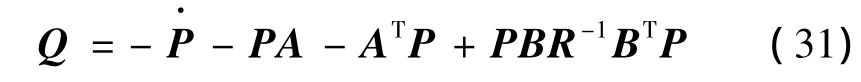
3 逆最優制導律中加權矩陣的求解

3．1 逆最優制導律對應的加權矩陣求解

對由式(5)～式(7)和式(9)構成的單輸入閉環制導系統，由于rank(NB)=rank(N)=rank(B)=1且矩陣NB的特征向量非正，滿足定理1的條件。由定理1中式(18)知，在性能指標函數J中，矩陣H、Q可設為對稱的，矩陣R設為正的線性時變的標量R(t)。由于NB也是標量，由定理2知，每一個正的R(t)都能保證RNB是對稱的。根據式(29)可知，矩陣Y是對稱陣，且BTY=0，設矩陣Y的形式為

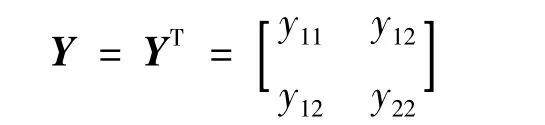
將Y帶入BTY=0中，有

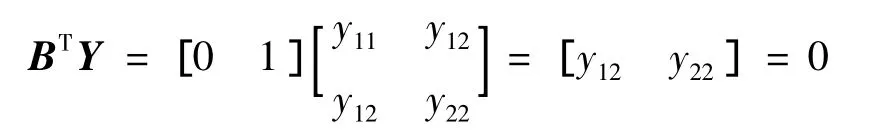
上式表明y12=y22=0，則矩陣Y可表示為

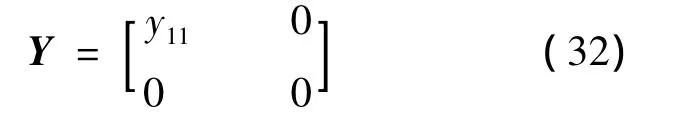
其中，y11為任意實數。

對任意給定的R(t)，定理3給出了實對稱矩陣P的解。將矩陣Y、N、B以及標量R(t)帶入式(30)中，求得矩陣P:

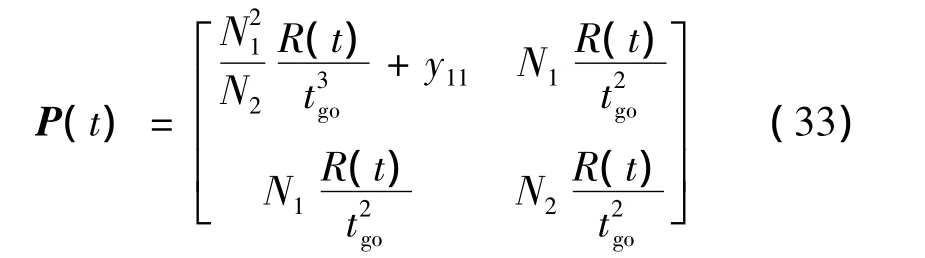
由于性能指標J*對所有的初值x0和t0都大于0，因此矩陣P也應為正定的，故要求y11＞0。為后續推導的方便，觀察式(33)，不妨令

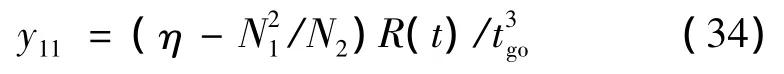
這樣，矩陣P又可表示為

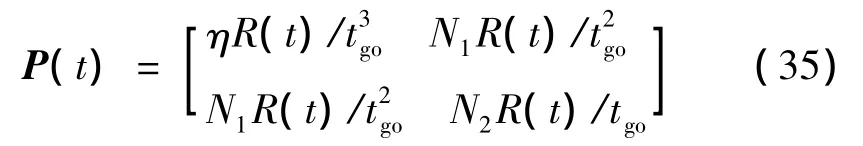
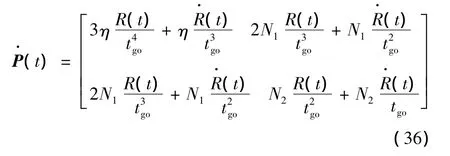
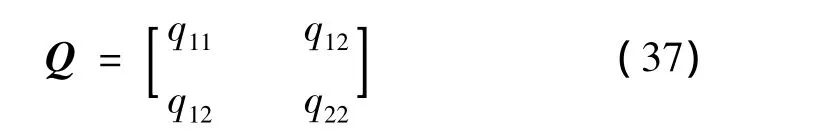
其中，Q的3個元素分別為

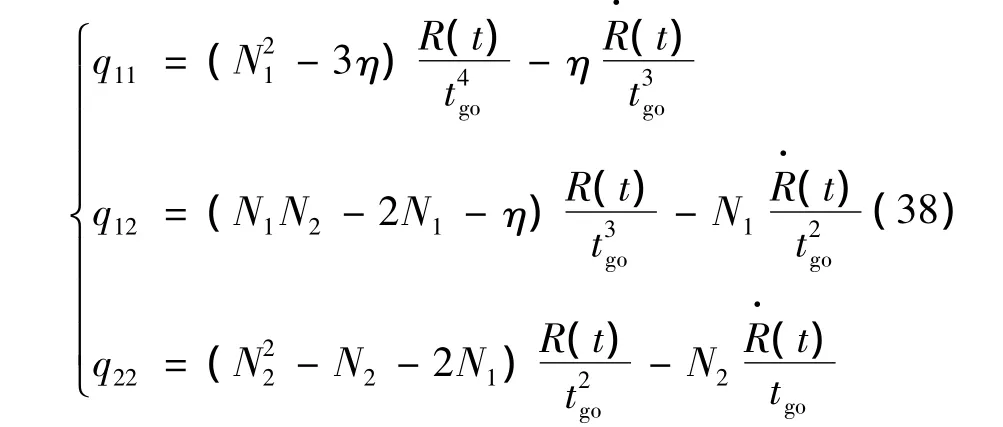
由于H=P(tf)，式(35)～式(38)即完成了逆最優問題中加權矩陣的構造。根據式(35)～式(38)，通過選取不同的η和R(t)，則可得到多組不同的［H，Q，R］。

3．2 加權矩陣求解的舉例說明

下面對上述結果舉例說明。不妨將R(t)取為表2中的形式，即

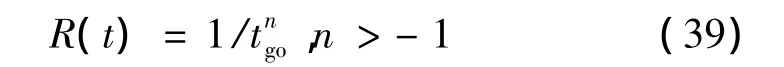
考慮矩陣Q的一種簡單情況，即Q為對角陣，則式(38)中q12=0。將上式的R(t)帶入q12，得

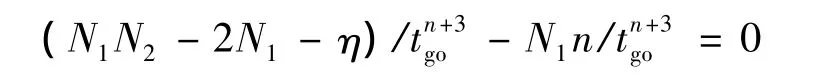
求解得

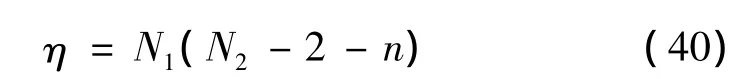
同時，η還需滿足條件η＞N21/N2，亦即

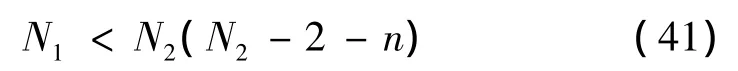
此時，矩陣P、Q分別為

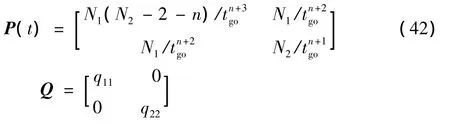
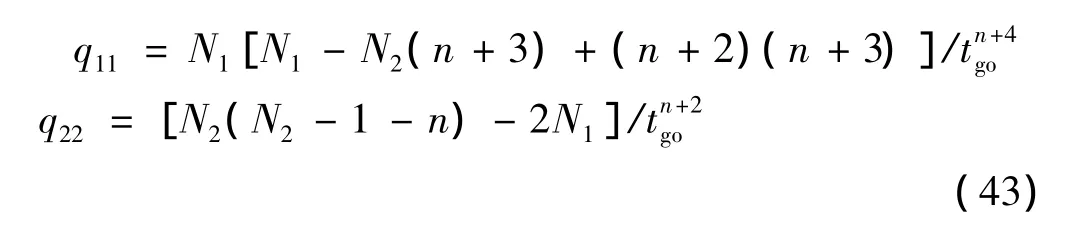
由式(43)可看出，若進一步使Q=0，則相當于在性能指標式(14)中不考慮狀態約束。令式(43)中q11=q22=0，求得 N1、N2的值為

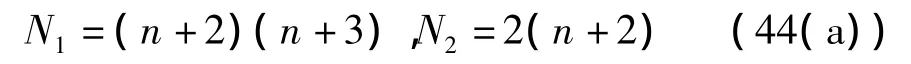
或

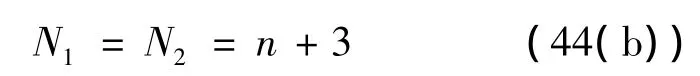
對比表2中的表達式可知，式(44(a))、式(44(b))的導航系數分別對應EPNGL和EOGLIAC兩種制導律，此時，與式(44(a))、式(44(b))對應的矩陣P分別為

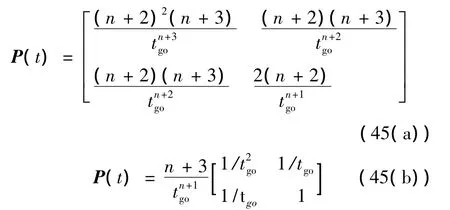
觀察式(45(a))、式(45(b))可看出，只要 n＞－1，在末段時刻 tf處，P→∞;又由于 H=P(tf)，則 H可表示為

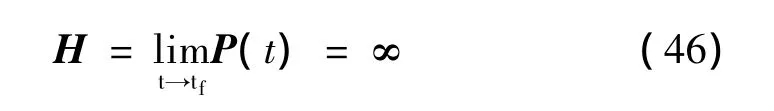
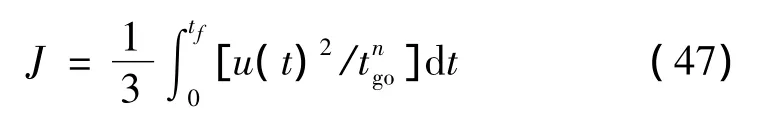
由前述的推導和分析可看出，對式(8)所述的制導律，通過選取合適的η和R(t)，任意大于零的導航系數N1、N2都可能是特定條件下的最優結果。這樣，通過制導律中逆最優問題的研究，再次拓展了最優制導律的內涵。

4 不同特征根下的制導律制導特性分析

4．1 特征根選擇

根據式(11)及 N1=λ1λ2，N2=λ1+λ2－1，相對地面坐標系的逆最優制導律可表示為

可進一步表示成以導引頭敏感的彈目視線角q、彈目視線角速率的形式:

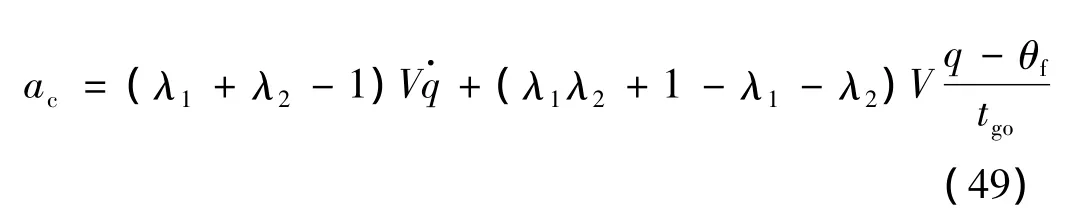
其中，ac為加速度指令。

根據式(44)的結果，容易計算得到EPNGL和EOGLIAC對應的特征根分別為λ1=n+3，λ2=1和λ1=n+3，λ2=n+2。

為研究不同特征根下的制導特性，并使研究具有代表性，特征根的選取如表3所示。其中，③、⑥分別對應EPNGL和EOGLIAC。

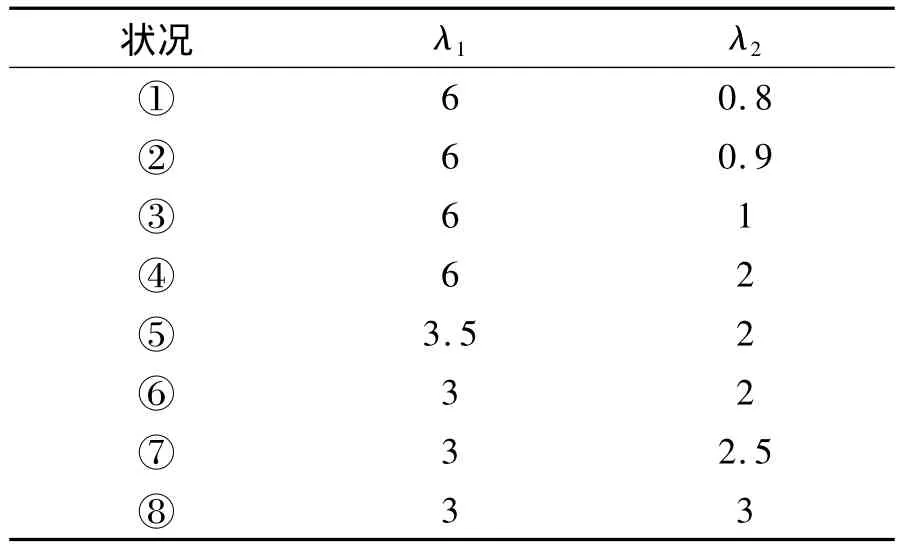
表3 選取的典型特征根Table 3 Chosen value of CR

4．2 制導特性對比分析

引入一階駕駛儀動力學1/(Tgs+1)，研究制導律在特征根變化時(如表1所示)的制導特性。據式(49)所示的制導律，構造圖3所示的制導系統模型，其中，初始方向誤差角 ε=5°，落角約束 θf= －45°，Tg=0．5 s，V=300 m/s．

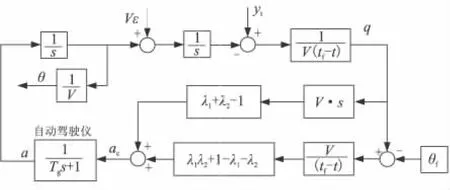
圖3 制導系統結構框圖Fig．3 Block diagram of guidance system

圖4～圖6分別為不同特征根作用下的彈道、彈道傾角及加速度曲線。為了使對比更直觀，圖6中沒有考慮駕駛儀動力學對加速度的影響。由圖4～圖6可看出，特征根的不同取值決定了制導律是否具有約束終端落角的能力;當特征根取值靠近EOGLIAC的特征根時，所對應的制導律對終端落角的約束也越嚴格，而當特征根取值靠近EPNGL的特征根時，所對應的制導律已經完全失去了對落角的約束能力。

需要強調的是，盡管每一對可能的(λ1，λ2)取值都能找到最優解釋，但這并不能保證其都能達到與EPNGL或EOGLIAC類似的制導性能，但特征根取值越靠近EPNGL或EOGLIAC，則所對應的制導律特性與EPNGL或EOGLIAC也越接近。

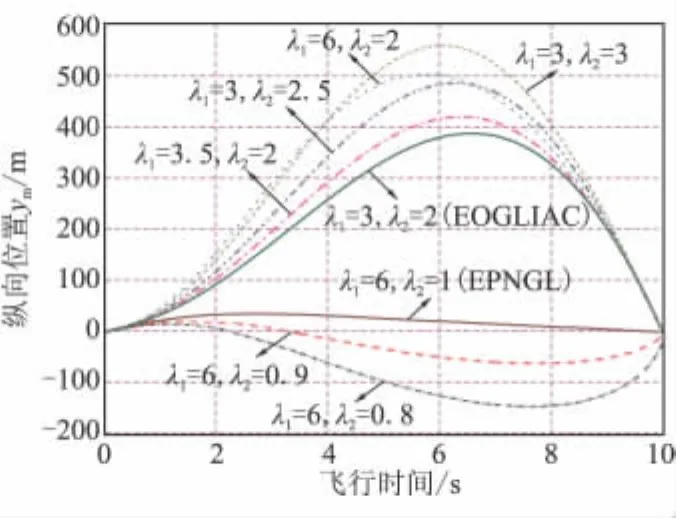
圖4 不同特征根下的彈道對比曲線Fig．4 Comparison of the trajectories for different CR

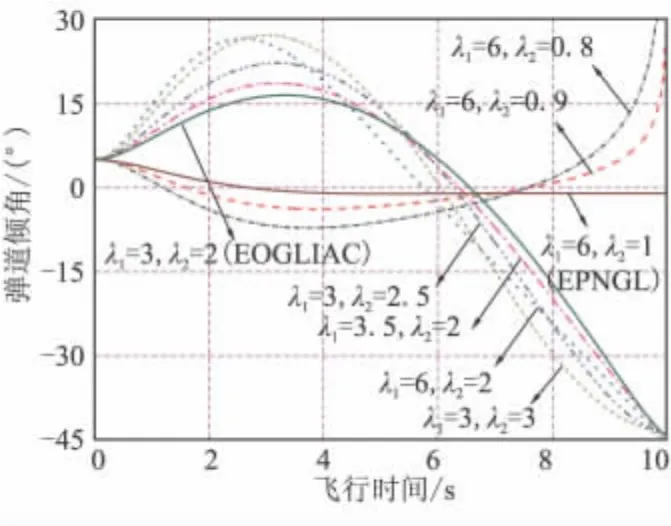
圖5 不同特征根下的彈道傾角對比曲線Fig．5 Comparison of the flight path angles for different CR

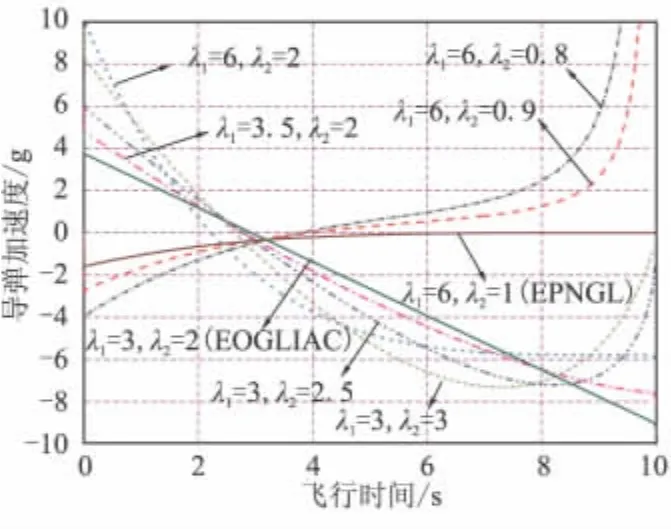
圖6 不同特征根下的加速度對比曲線Fig．6 Comparison of the accelerations for different CR

圖7、圖8所示的不同特征根下的脫靶量和終端落角誤差曲線也直接印證了上述結論。

因此，盡管逆最優制導律的提出將制導律的2個特征根(或導航系數)從有限的點/線擴展到幾乎所有的正實根，但對任意選擇的一對特征根，并不能保證其一定具有與EPNGL、EOGLIAC等類似的制導性能，每一對特征根都需要精細的挑選和嚴格的考核，而以EPNGL、EOGLIAC等為典型代表的常規最優制導律已經得到廣泛的應用，經過了充分的工程檢驗，在這個意義上，EPNGL、EOGLIAC等還是工程最優的。

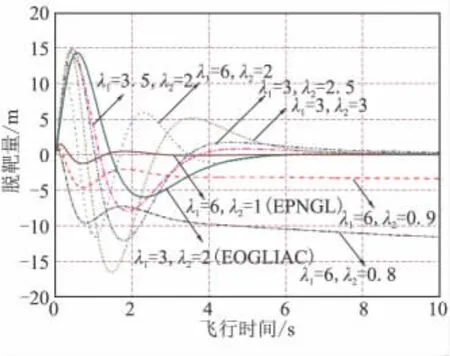
圖7 不同特征根下的脫靶量對比曲線Fig．7 Comparison of the miss-distances for different CR

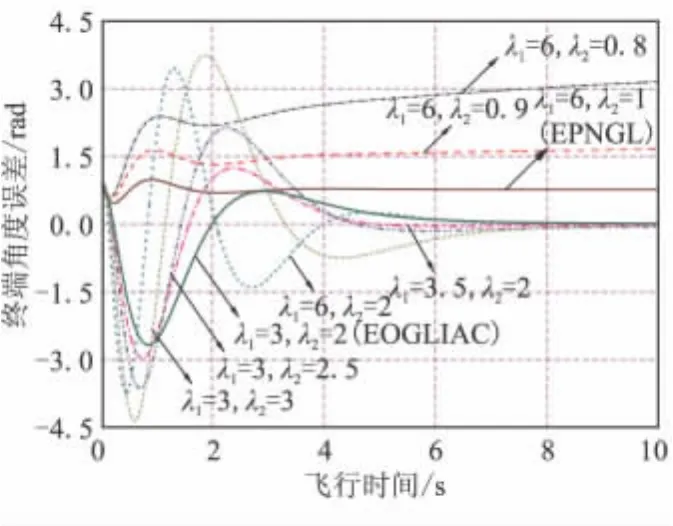
圖8 不同特征根下的終端角度誤差對比曲線Fig．8 Comparison of the terminal impact angle errors for different CR

5 結論

(1)通過建立相對于終端彈目連線的導彈運動方程，概括了典型的能量最優制導律，分析了其特征根分布范圍。將制導律的2個特征根從有限的點/線擴展到幾乎所有的正實根，提出了制導律的逆最優問題。詳細討論了逆最優問題中性能指標加權矩陣的構造過程，給出了加權矩陣和Riccati矩陣的計算公式。通過將控制權矩陣選為time-to-go的負n次冪函數的形式，對加權矩陣的求解進行了舉例說明。

(2)選取了多組具有代表性的特征根，對不同特征根下制導律的制導特性進行了全面的仿真研究。研究結果表明，盡管每一對可能的特征根取值都能找到最優解釋，但這并不能保證其都能達到與EPNL或EOGLIAC類似的制導性能，特征根取值越靠近EPNGL或EOGLIAC，則所對應的制導律特性與EPNGL或EOGLIAC也越接近。但特征根的取值范圍要滿足哪些限制條件才能達到與EPNGL或EOGLIAC類似的性能，尚有待于后續進一步的研究。盡管如此，文中通過逆最優問題的研究，拓展了最優制導律的內涵。

［1］ Zarchan P．Tactical and strategic missile guidance，5th edition［M］．Virginia:AIAA Inc．，2007:31-50，541-569．

［2］ Garnell P．Guided weapon control systems［M］．Beijing:Beijing Institute of Technology，2003:297-364．

［3］ Ryoo C K，Shin H S，Tahk M J．Energy optimal waypoint guidance synthesis for antiship missiles［J］．IEEE Transactions on Control Systems Technology，2010，46(1):80-95．

［4］ Ohlmeyer E J，Phillips C A．Generalized vector explicit guidance［J］．Journal of Guidance，Control，and Dynamics，2006，29(2):261-268．

［5］ Ryoo C K，Cho H，Tahk M J．Time-to-go weighted optimal guidance with impact angle constraints［J］．IEEE Transactions on Control Systems Technology，2006，14(3):483-492．

［6］ Ryoo C K，Cho H，Tahk M J．Optimal guidance laws with terminal impact angle constraint［J］．Journal of Guidance，Control，and Dynamics，2005，28(4):724-732．

［7］ Ratnoo A，Ghose D．State dependent Riccati equation based guidance law for impact angle constrained trajectories［J］．Journal of Guidance，Control，and Dynamics，2009，32(1):320-325．

［8］ Ratnoo A，Ghose D．Impact angle constrained interception of nonstationary nonmaneuvering targets［J］．Journal of Guidance，Control，and Dynamics，2010，33(1):269-275．

［9］ Ben-Asher J Z，Yaesh I．Advances in missile guidance theory［M］．Virginia:AIAA Inc．，1998:25-88．

［10］ Lee Y I，Kim S H，Tahk M J．Optimality of linear time-varying guidance for impact angle control［J］．IEEE Transactions on Aerospace and Electronic Systems，2012，48(3):2802-2817．

［11］ Kalman R E．When is a linear control system optimal［J］．Journal of Basic Engineering，1964，Series D(86):51-60．