翼傘轉彎機理及其影響因素仿真分析

李德榮，陳 楸，吳澤銳，于群濤

（西北工業大學 自動化學院，陜西 西安 710129）

與傳統降落傘相比，翼傘具有良好的滑翔性能、穩定性和可操縱性等特點[1]，這使得翼傘空投系統可從遠距離高空投放點精確地將物資裝備投送到預定地點，達到定點、無損的要求。鑒于翼傘在空投作業上的突出優勢，翼傘空投系統被廣泛應用到部隊兵力裝備的投送、飛行器的回收和人道主義救援等方面。

為了提高翼傘系統的航向安定性，翼傘系統可在傘衣后緣中部連接尾傘，或在傘衣兩側邊緣設計安定面[2]，德國ALEX系統在傘艙尾部也加裝了類似飛機垂尾的安定面。除設計方法外，翼傘自身的拱形結構是保持系統航向安定性的關鍵因素。但翼傘航向安定性是有一定范圍的，否則會對翼傘的轉彎特性造成不利影響。本文系統分析了翼傘轉彎的機理，建立了翼傘系統六自由度動力學模型，通過數值仿真，詳細分析了翼傘航向安定性和阻力方向舵對翼傘轉彎特性的影響。結果表明只有兩者相互匹配時，才能夠提供良好的轉彎性能。

1 翼傘動力學模型的特點

1.1 翼傘建模的特點

為了便于研究，本文建立了翼傘系統六自由度仿真模型，其動力學方程可通過動量和動量矩定理獲得。建模過程中要考慮到翼傘區別于飛機的結構特點，翼傘的重心較低且傘衣輕質柔軟易變形，同時必須將翼傘在空氣中所受到的附加質量影響考慮進來，本文采用的是Lissaman[3]提供的附加質量矩陣形式。翼傘動力學方程的具體推導過程在文中不再贅述，可參見文獻[4-5]。

像其它飛行器建模一樣，可以將翼傘看作剛體。但由于翼傘的結構特點，翼傘作為剛體的適用范圍是有限的。如圖 1所示，翼傘的傘繩匯集到吊掛物上，傘繩呈三角形分布。由于傘繩只能傳遞拉力，不能傳遞壓力，所以經過傘繩所能傳遞的力的方向只能限定在這個三角形的范圍內。

圖 1中吊掛物處于位置a時，受力不可能平衡，翼傘系統向右下方平行移動。此時，傘衣上受到的空氣阻力遠大于吊掛物上所受到的空氣阻力，形成使翼傘系統逆時針轉動的力矩。翼傘系統的合成運動基本上是以傘衣為中心的擺動，吊掛物將擺動到b點，而傘衣的運動相對于吊掛物的運動要小得多。此外，一般翼傘系統的傘繩都很長，以降低擺動的頻率。因此，在翼傘建模時，將機體系的坐標原點放在傘衣上某處比放在系統的質心更方便。氣動力的力矩都是按氣動焦點計算的，為了避免重新計算氣動力的力矩，可以將坐標原點放在氣動焦點處。

將機體系的坐標原點放在質心以外的位置，系統的轉動慣量需要按平移定律進行修正。重力對坐標原點的力矩很自然地表現出對系統姿態的穩定作用。

1.2 翼傘的縱向運動特性

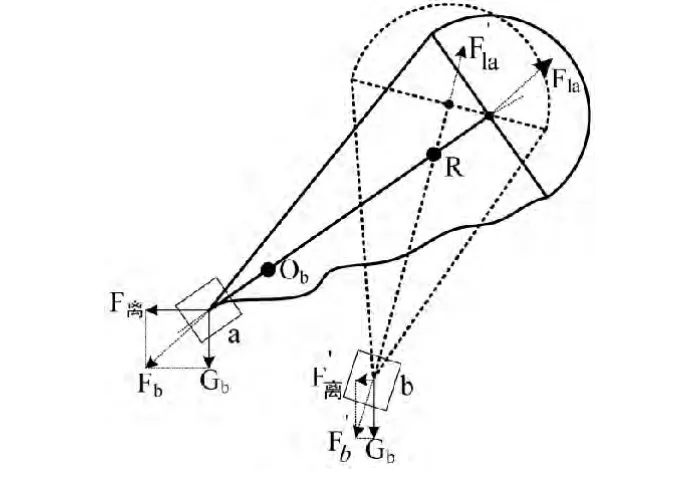
圖1 翼傘的建模特點Fig.1 Modeling features of parafoil

對于飛機可以按機身的軸線和翼尖的連線來定義機體坐標系，而翼傘系統的機體坐標就不這么明顯了。我們可以想象，如果沒有阻力，翼傘系統在穩定平飛時，氣動力和重力將在一條鉛垂線上。我們可以用這條鉛垂線來定義翼傘系統的機體坐標系。由于氣動力的壓力中心隨著迎角和側滑角而改變，為方便起見，我們選擇氣動焦點作為機體系的坐標原點。以氣動焦點到系統質心的連線作為機體系的z軸。在縱向對稱面內，以z軸的垂直線為x軸，方向指向翼傘的前緣。按右手定則確定y軸。

翼傘的安裝角定義為翼面弦線與x軸的夾角。同滑翔機一樣，翼傘的安裝角應該是負的，即翼的前緣低于后緣。如此，氣動力的合力Fp前傾，其水平分量F成為系統前飛的“牽引力”。當翼傘從靜止狀態開始下落時，自然穩定的狀態使機體系的Oxy平面基本上在水平面內，速度方向垂直向下。由于翼面弦線前傾，其上的氣動力也是前傾的，氣動力的水平分量使翼傘系統獲得前飛的加速度。當前飛速度足夠大時，升力與重力平衡，達到穩態。這時，翼傘系統有確定的滑翔速度和滑翔比。對于同樣的翼傘，不同的翼載比及（或）不同的安裝角，將有不同的滑翔速度和滑翔比。

圖2中翼傘系統處于穩定滑翔狀態。翼傘氣動升力Lp和阻力Dp按翼坐標系分解，阻力沿弦向，升力與弦向垂直。載荷重力Gb垂直向下，阻力Db水平向后。穩定滑翔時，系統沿傘衣焦點與載荷質心的連線pb受力平衡：

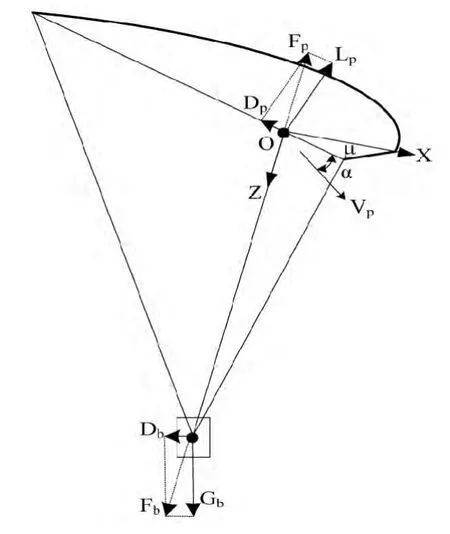
圖2 翼傘的縱向運動特性Fig.2 Longitudinal motion characteristics of parafoil

1.3 翼傘的橫向運動特性

翼傘后緣的左右兩側可以分別由兩根操縱繩下拉以實現對翼傘飛行軌跡的控制。當左側后緣下拉時，左側阻力增大，產生負的偏航力矩，使翼傘前緣向左轉動，出現正的側滑角。翼傘系統應有適當的航向安定性，出現側滑時會產生一個減小側滑趨勢的回復力矩。對于一定的操縱量，在操縱力矩和回復力矩的共同作用下，翼傘系統將穩定在一個確定的側滑角上。如圖 3所示，此時氣動力的水平分量F可以分解為切向力Ft和法向力Fn，其中法向力提供了轉彎所需的向心力。

翼傘后緣左側下拉時，其升力也會增加，產生一個正的滾轉力矩，使翼面略向外傾，這是不利于轉彎的。但由于翼傘系統的重心很低，正常情況下，這種作用很弱。

綜上所述，翼傘系統以側滑轉彎為主。為了達到適當的側滑角，翼傘的操縱力矩和航向安定性回復力矩的匹配是一個關鍵因素。本文對此進行了仿真分析。

圖3 翼傘的橫向運動特性Fig.3 Lateral motion characteristics of parafoil

2 翼傘的舵效和航向安定性

在影響翼傘轉彎性能的諸多因素中，翼傘的舵效和航向安定性是影響其轉彎性能的重要因素。兩者對轉彎性能的影響主要體現在偏航力矩上。偏航力矩系數表達式如下：

從式（2）可以看出，翼傘系統的偏航力矩主要由操縱偏航力矩和偏航回復力矩組成，氣動系數分別為 Cnδr（δr）和 Cnβ（β），代表了阻力方向舵的舵效和翼傘的航向安定性。當上述兩種偏航力矩匹配時，系統才會產生合適的側滑角，形成穩定的轉彎。

圖4是翼傘阻力方向舵的操縱特性，整體呈非線性關系。當翼傘單側下拉量很小趨近于0時具有死區特性，此時翼傘沒有轉彎的趨勢；當翼傘單側下拉量很大趨近于1.0時具有飽和特性，在趨于飽和范圍內的翼傘舵效對轉彎狀態的影響差別不大。阻力方向舵的舵效對阻力系數的影響比較大，當翼傘后緣單側下拉時，翼傘兩側產生的阻力大小不同，下拉一側的阻力要大于另一側，因此產生了朝向下拉一側的偏航力矩。右側下偏時產生正的偏航力矩，翼傘往右轉彎；左側下偏時產生負的偏航力矩，翼傘往左轉彎。

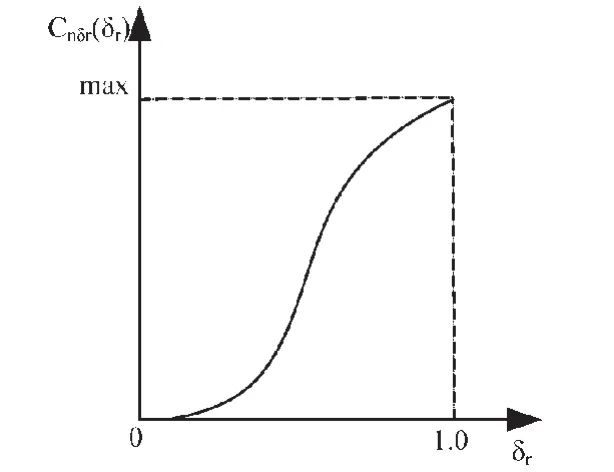
圖4 阻力方向舵操縱特性Fig.4 The handling characteristic of drag rudder

圖 5是翼傘的航向安定性特性，3條曲線分別代表了航向安定性不同的3種翼傘，整體呈非線性關系。對于同一種翼傘，側滑角越大，翼傘的偏航回復力矩越大，但側滑角是有限度的，當翼傘的側滑角超過25°時，翼傘的航向安定性效果急劇變差，轉彎狀態變得不穩定。

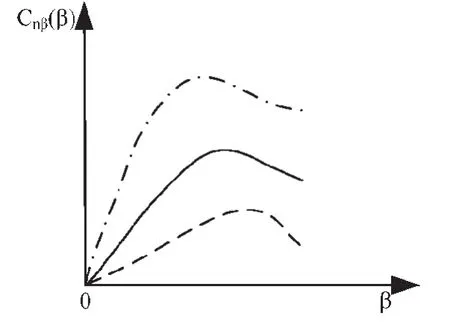
圖5 航向安定性特性Fig.5 The characteristic of directional stability

航向安定性特性曲線的斜率為航向靜穩定性導數，表達式如下：

它是衡量翼傘航向安定性的重要參數。翼傘在飛行過程中受風擾動或轉彎操縱時會產生側滑角β，同時翼傘航向也會發生變化，此時翼傘會通過Cnβ產生偏航回復力矩阻止側滑角β增加，翼傘系統重新進入平衡狀態，這種作用效果來自翼傘的展向拱形結構[6-7]。下面將仿真分析航向安定性對翼傘轉彎性能的影響。

3 仿真實驗

翼傘系統進行遠距離空投作業時，要根據位置、風向信息和任務規劃不斷消除側向誤差，進行航跡控制，以達到精確安全著陸的目的，此過程須進行轉彎操縱控制。

下面將通過仿真實驗研究翼傘航向安定性和操縱力矩對翼傘轉彎性能的影響。表1為翼傘的基本結構參數。

仿真實驗選取 Cnβ=10-5/deg、10-2/deg和 10-1/deg 3個值，分別代表航向安定性不足、合適和過強的3種不同翼傘；左側下拉量δr選取0.2～1.0 9個操縱量。仿真開始時，翼傘系統從6 000 m高空穩定滑翔50 s后進行轉彎操縱，穩定后的測試結果如圖 6～圖 8所示。

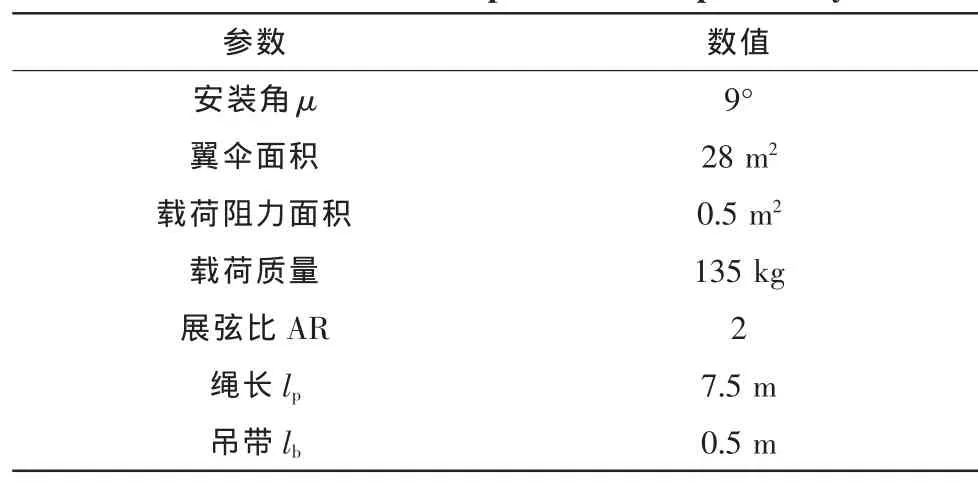
表1 翼傘系統基本結構參數Tab.1 The basis structure parameters of parafoil system

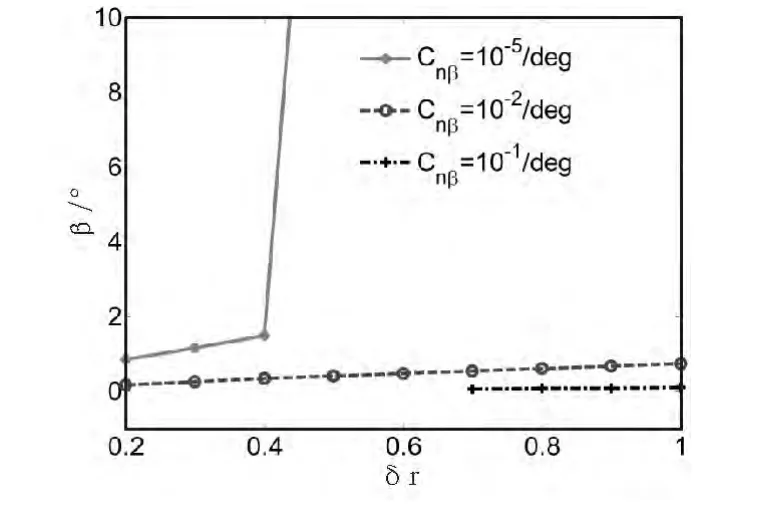
圖6 翼傘側滑角βFig.6 The side-slip angle β of parafoil

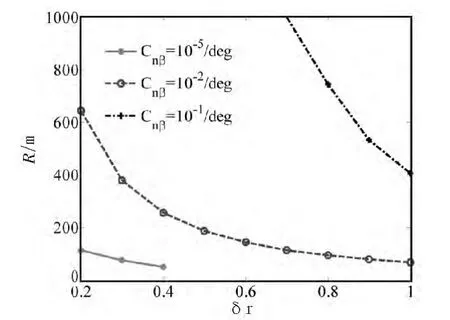
圖7 翼傘轉彎半徑RFig.7 The turn radius R of parafoil

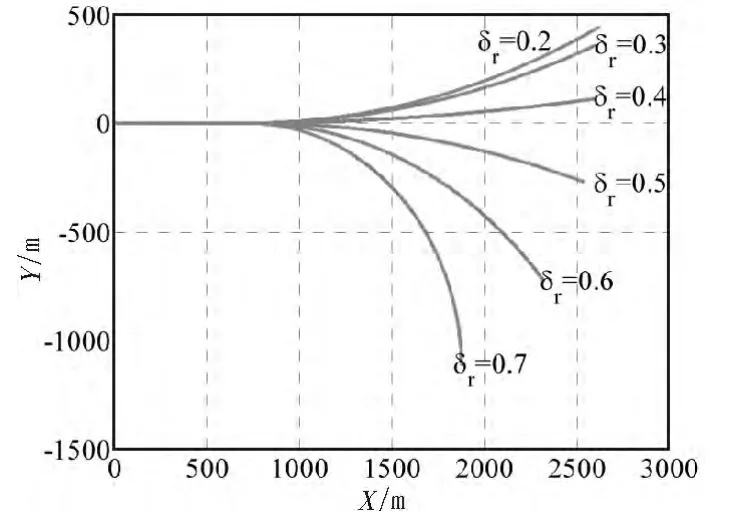
圖8 安定性過強時的反轉情況Fig.8 Reverse turn when excess of directional stability

圖6 、圖 7表明了翼傘航向安定性和單側下拉量都會影響到翼傘的轉彎狀態。圖6中安定性過強翼傘的側滑角和圖7中安定性不足翼傘的轉彎半徑只畫出了可正常轉彎時值。在以上兩圖中，對于航向安定性合適的翼傘，隨著單側下拉量的增加，翼傘側滑角增加，轉彎半徑減少。

從圖 6中明顯看出，當翼傘安定性不足時，較小的操縱量就會使側滑角變得極大。當δr=0.4時，側滑角為1.5°，而δr超過0.4后，翼傘側滑角變得極大，這種情況是由于翼傘的操縱力矩遠大于偏航回復力矩所致。

從圖 7中明顯看出，當翼傘安定性過強時，翼傘即使在較大操縱量時轉彎半徑也很大。如圖所示，當δr小于0.7時，轉彎半徑就已超過了1 000 m，此時翼傘變得難以轉彎。單側下拉量較小甚至出現了逆向轉彎的情況，如圖 8所示，δr≥0.5時，翼傘正常往左轉彎，但當δr≤0.4時，翼傘往右轉彎，這種情況是由于偏航力矩遠大于操縱力矩所致，而隨著下拉量逐漸增大，操縱力矩增加，翼傘恢復左向轉彎。

根據對仿真結果的分析，我們可以得出：翼傘航向安定性不足或者過強都會影響到翼傘的轉彎性能。只有翼傘的航向安定性和操縱力矩匹配時才會有良好的轉彎性能，才能實現翼傘系統的精確空投。

4 結束語

影響翼傘轉彎性能的因素有很多，文中在深入分析翼傘轉彎機制的基礎上，重點研究了翼傘的航向安定性和阻力方向舵對轉彎性能的影響，所得結論可為翼傘系統轉彎狀態研究提供有益的理論參考。

[1]秦子增，葛玉君.可控翼傘飛行轉彎控制性能仿真初步研究[J].宇航學報，1993（1）：89-96.QIN Zi-zeng，GE Yu-jun.Preliminary simulation of flight turn performance of controllable parafoil systems[J].Journal of Astronautics，1993（1）：89-96.

[2]Ward M，Costello M，Slegers N.Specialized System Identification for Parafoil and Payload Systems[J].Journal of Guidance， Control， and Dynamics，2012，35（2）：48-50.

[3]Lissaman P B S，Brown G J.Apparent mass effects on parafoil dynamics[R].AIAA-93-1236：10-13.

[4]Toglia C，Vendittelli M.Modeling and motion analysis of autonomous paragliders[J].Department of Computer and System Sciences Antonio Ruberti Technical Reports，2010，2（5）：32-35.

[5]焦亮，孫青林，亢曉峰.翼傘空投機器人系統的六自由度仿真[J].計算機仿真，2011，28（001）:39-42.JIAO Liang，SUN Qing-lin，KANG Xiao-feng.Simulation of 6-DOF parafoil and air-dropped robot system[J].Computer Simulation，2011，28（001）:39-42.

[6]Nicolaides J D.Parafoil wind tunnel tests[R].Notre Dame Univ in Dept of Aerospace and Mechanical Engineering，1971.

[7]Strickert G，Witte L.Analysis of the relative motion in a parafoil-load-system[R].AIAA，2001-2013.