應(yīng)力釋放技術(shù)識(shí)別在役鋼筋混凝土構(gòu)件內(nèi)力(I)——方法研究

魯 亮 李 鴻 劉紀(jì)軍

(1.同濟(jì)大學(xué)結(jié)構(gòu)工程與防災(zāi)研究所，上海200092;2.上海市機(jī)電設(shè)計(jì)研究院有限公司，上海200040)

1 引 言

我國(guó)城鎮(zhèn)現(xiàn)有存量建筑總面積超過(guò)200億平方米，由于設(shè)計(jì)、施工、壽命期等各種原因，有15%以上的建筑需要檢測(cè)、鑒定與加固。在西方發(fā)達(dá)國(guó)家，建筑維修和加固費(fèi)用約占其土建總投資的50%。既有建筑、橋梁等混凝土結(jié)構(gòu)的安全性評(píng)估中，混凝土結(jié)構(gòu)的受力狀態(tài)是一個(gè)十分重要的評(píng)估內(nèi)容。目前鋼筋混凝土結(jié)構(gòu)的安全性評(píng)估主要以分析計(jì)算為主［1］，輔以靜載試驗(yàn)和材料強(qiáng)度檢測(cè)結(jié)果，所建立的數(shù)值分析模型是處于理想狀態(tài)的，沒(méi)有充分考慮影響構(gòu)件內(nèi)力狀態(tài)的不利因素，比如施工帶來(lái)的尺寸偏差、外加荷載分布的不均勻性、材料特性在整個(gè)結(jié)構(gòu)內(nèi)分布的均勻性、結(jié)構(gòu)的變形狀態(tài)等。用處于理想狀態(tài)的分析模型計(jì)算得到的構(gòu)件內(nèi)力比實(shí)際內(nèi)力偏大或偏小，依據(jù)計(jì)算結(jié)果進(jìn)行結(jié)構(gòu)加固不能保證結(jié)構(gòu)的抗震承載力安全，所以需要尋找一種現(xiàn)場(chǎng)實(shí)測(cè)構(gòu)件內(nèi)力的方法。構(gòu)件表面應(yīng)力釋放法是一種值得探討的現(xiàn)場(chǎng)實(shí)測(cè)方法，采用應(yīng)力釋放法測(cè)試混凝土表面工作應(yīng)力，抽樣測(cè)試結(jié)果可以與計(jì)算結(jié)果進(jìn)行比較，并可以用來(lái)對(duì)整個(gè)結(jié)構(gòu)的內(nèi)力計(jì)算結(jié)果進(jìn)行修正，最終得到符合實(shí)際的構(gòu)件內(nèi)力分布［2］。

表面應(yīng)力釋放法廣泛應(yīng)用于鋼構(gòu)件表面殘余應(yīng)力的測(cè)試，已有相關(guān)測(cè)試規(guī)范和標(biāo)準(zhǔn)，是一種比較成熟的測(cè)試技術(shù)。表面應(yīng)力釋放法用于測(cè)試混凝土表面工作應(yīng)力尚有技術(shù)和理論上障礙，已有學(xué)者進(jìn)行了相關(guān)研究［3］，但是研究成果離工程應(yīng)用尚有一定距離。本文就應(yīng)力釋放技術(shù)用于測(cè)試混凝土構(gòu)件內(nèi)力的基本原理做理論闡述。

2 應(yīng)力釋放法測(cè)試在役構(gòu)件表面應(yīng)力

應(yīng)力釋放法是在構(gòu)件表面鉆一個(gè)小孔或開(kāi)一根槽，使得孔邊或槽邊應(yīng)力得以釋放，通過(guò)應(yīng)變電測(cè)的方法得到釋放應(yīng)變后反推測(cè)點(diǎn)表面原有應(yīng)力的方法。應(yīng)力釋放的方法有很多種，常用的有鉆孔法、盲孔法、環(huán)孔法、開(kāi)槽法等。鉆孔法和盲孔法是兩種常用的應(yīng)力釋放方法，該方法最早是由德國(guó)學(xué)者M(jìn)athar于1934年提出［4］，后經(jīng)Soete［5］等學(xué)者發(fā)展完善而形成系統(tǒng)理論。1981年美國(guó)材料與試驗(yàn)協(xié)會(huì)將盲孔法納入ASTM標(biāo)準(zhǔn)E837-81［6］，1992年中國(guó)船舶工業(yè)總公司也將其制定為殘余應(yīng)力測(cè)試的中國(guó)船舶行業(yè)標(biāo)準(zhǔn)CB 3395-92［7］。此兩種方法主要用于金屬材料表面應(yīng)力的測(cè)試。由于混凝土材料是非勻質(zhì)材料，研究表明用鉆孔法或盲孔法得到的測(cè)試結(jié)果離散性很大，所以研究人員嘗試采用環(huán)孔法和開(kāi)槽法測(cè)試混凝土表面應(yīng)力。

2.1 環(huán)孔法

環(huán)孔法是由Milbred于1951年提出來(lái)的，其基本原理是對(duì)有初始約束應(yīng)力的測(cè)試構(gòu)件，采用機(jī)械切割的方法在測(cè)點(diǎn)的周?chē)懈钜蝗Γ獬郎y(cè)點(diǎn)周?chē)膽?yīng)力約束，圈內(nèi)的應(yīng)力逐步被釋放。在圈內(nèi)貼上應(yīng)變計(jì)，測(cè)得釋放的應(yīng)變，即可算出表面的應(yīng)力大小。該種方法原理比較簡(jiǎn)單，國(guó)內(nèi)有學(xué)者采用此方法在混凝土構(gòu)件應(yīng)力測(cè)試方面做了相關(guān)研究。翁冠群［8］利用MSC/NASTRAN有限元軟件得出應(yīng)力釋放至零點(diǎn)的環(huán)孔深度與環(huán)孔直徑的數(shù)值關(guān)系，指出100 mm外徑的環(huán)形鉆孔其深度在30～35 mm之間時(shí)應(yīng)力逐漸釋放至零，并將環(huán)孔法用于橋梁預(yù)應(yīng)力損失的檢測(cè)中，同時(shí)指出33 mm可以作為合適的開(kāi)孔深度。劉永淼［9］采用混凝土取芯機(jī)開(kāi)環(huán)孔實(shí)現(xiàn)應(yīng)力解除，在試驗(yàn)室完成了既有混凝土構(gòu)件正應(yīng)力測(cè)量試驗(yàn)。

環(huán)孔法操作簡(jiǎn)單、易行，缺點(diǎn)在澆筑構(gòu)件時(shí)需預(yù)埋導(dǎo)線(xiàn)，否則采集釋放數(shù)據(jù)時(shí)在布線(xiàn)方面存在困難，故此方法可用于試驗(yàn)室科學(xué)研究，不易在實(shí)際工程中推廣使用。

2.2 開(kāi)槽法

開(kāi)槽法是由環(huán)孔法發(fā)展而來(lái)。該方法用四條長(zhǎng)槽解除測(cè)點(diǎn)約束，該處的應(yīng)力即被釋放，原應(yīng)力場(chǎng)失去平衡，這時(shí)測(cè)點(diǎn)周?chē)鷮a(chǎn)生一定量的釋放應(yīng)變(其大小與釋放應(yīng)力是相對(duì)的)，并使原應(yīng)力場(chǎng)達(dá)到新的平衡，形成新的應(yīng)力場(chǎng)和應(yīng)變場(chǎng)。測(cè)出釋放應(yīng)變?chǔ)う牛纯衫孟鄳?yīng)公式計(jì)算出初始測(cè)試點(diǎn)的應(yīng)力。對(duì)于圖1所示應(yīng)變計(jì)測(cè)得的釋放應(yīng)變，其應(yīng)變計(jì)算公式為［10］

圖1 開(kāi)槽法的應(yīng)變計(jì)粘貼方式Fig.1 Strain gauges paste way of grooving method

由于測(cè)量γyz比較困難，通常的做法是測(cè)定三個(gè)方向的線(xiàn)應(yīng)變，由這三個(gè)方向的線(xiàn)應(yīng)變，反解出γyz:

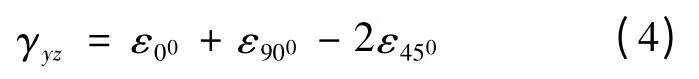
在求得測(cè)點(diǎn)的應(yīng)變后，利用平面應(yīng)力狀態(tài)時(shí)的胡克定律，求得測(cè)點(diǎn)的應(yīng)力:

式中，E，ν，G分別為被測(cè)材料的彈性模量、泊松比和剪切模量。

從上面推導(dǎo)可知，工作應(yīng)力測(cè)試的結(jié)果主要與兩個(gè)因素有關(guān)，第一個(gè)因素是材料屬性，第二個(gè)因素是電阻應(yīng)變片的測(cè)量值。

應(yīng)用應(yīng)變電測(cè)法可以測(cè)出以上釋放應(yīng)變值，此值是否是構(gòu)件表面原有應(yīng)變釋放至零的應(yīng)變值，有待進(jìn)一步試驗(yàn)或數(shù)值分析研究。此釋放應(yīng)變值與槽距、槽寬、槽深等因素有關(guān)，同時(shí)在應(yīng)變測(cè)試過(guò)程中會(huì)受到振動(dòng)擾動(dòng)、溫度變化、混凝土浸水等的影響，也有待進(jìn)一步探討。

國(guó)內(nèi)有學(xué)者采用此種方法在混凝土構(gòu)件正應(yīng)力測(cè)試方面做了相關(guān)研究工作。沈旭凱［11］通過(guò)對(duì)5根混凝土柱進(jìn)行開(kāi)槽法應(yīng)力釋放研究，指出采用開(kāi)槽法進(jìn)行應(yīng)力釋放可以得到與環(huán)孔法一樣的效果;王柏生等［12］采用切割兩條長(zhǎng)槽的方式釋放混凝土構(gòu)件的正應(yīng)力，通過(guò)有限元軟件分析了工作應(yīng)力隨開(kāi)槽深度的變化規(guī)律，與環(huán)孔法進(jìn)行了比較，得到了正應(yīng)力完全釋放的開(kāi)槽深度;并且在分析了各種影響因素后，就開(kāi)槽引起的擾動(dòng)應(yīng)變展開(kāi)試驗(yàn)研究，據(jù)此估計(jì)檢測(cè)時(shí)的擾動(dòng)應(yīng)變，并進(jìn)行了驗(yàn)證性試驗(yàn)，消除了檢測(cè)結(jié)果中的擾動(dòng)應(yīng)變，取得了滿(mǎn)意的結(jié)果。

3 既有鋼筋混凝土構(gòu)件內(nèi)力識(shí)別基本理論

建筑結(jié)構(gòu)混凝土構(gòu)件的基本形式有梁、柱、板、墻四種，四種構(gòu)件形式截面內(nèi)力分量的數(shù)量不同，墻主要有面內(nèi)剪力和彎矩，板主要有面內(nèi)軸力和面外彎矩，而梁、柱最多有軸力、雙橫向剪力、雙橫向彎矩和扭矩六個(gè)內(nèi)力分量，下面以一個(gè)含鋼筋截面的混凝土柱為例，見(jiàn)圖2，推導(dǎo)在內(nèi)力作用下產(chǎn)生于構(gòu)件表面中點(diǎn)處的正應(yīng)變和剪應(yīng)變公式，再由測(cè)試得到的釋放應(yīng)變值反推構(gòu)件截面內(nèi)力值，以證明表面應(yīng)力釋放技術(shù)的可行性。

圖2 矩形截面構(gòu)件受力簡(jiǎn)圖Fig.2 Force diagram of rectangular section member

3.1 鋼筋混凝土矩形截面構(gòu)件在軸力、彎矩作用下的應(yīng)力表達(dá)式

在圖2所示軸力Fz、作用下，截面四邊中點(diǎn)1、2、3、4處僅產(chǎn)生正應(yīng)力，如下:

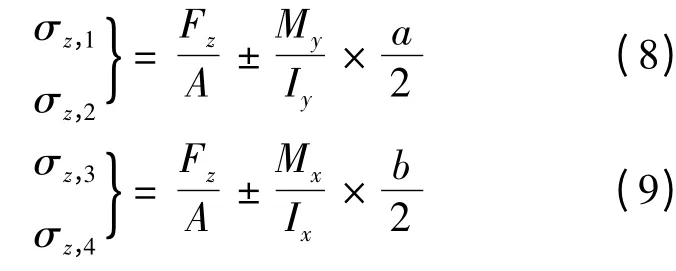
式中 a、b——截面邊長(zhǎng);

3.2 均質(zhì)材料矩形截面構(gòu)件在扭矩作用下的剪應(yīng)力表達(dá)式

扭矩作用下含鋼筋截面的剪應(yīng)力公式推導(dǎo)相對(duì)復(fù)雜，先從勻質(zhì)材料開(kāi)始，最后考慮用修正的方法得到含鋼筋截面的剪應(yīng)力表達(dá)式。由于非圓截面構(gòu)件扭轉(zhuǎn)時(shí)截面將發(fā)生翹曲，作為材料力學(xué)一維簡(jiǎn)化理論之基礎(chǔ)的平截面假定不再適用，所以非圓截面構(gòu)件的扭轉(zhuǎn)問(wèn)題要用二維彈性力學(xué)方法來(lái)推導(dǎo)。

矩形截面構(gòu)件受扭矩Mz作用，如圖3所示，其剪應(yīng)力表達(dá)式為［13］

式中，G為材料的剪切模量，

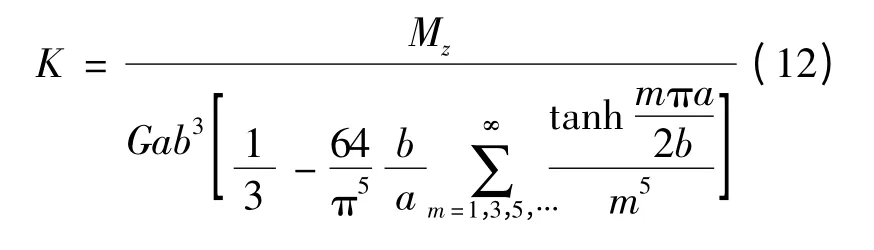
圖3 矩形截面構(gòu)件受扭Fig.3 Rectangular section member subjected to torsion

令式(10)中y=±b/2，得到AB、CD邊的剪應(yīng)力表達(dá)式:

令式(11)中x=±a/2，得到BC、AD邊的剪應(yīng)力表達(dá)式:

最大應(yīng)力發(fā)生在長(zhǎng)邊中點(diǎn)處，令式(10)中x=0，y=±b/2，得到點(diǎn)3處和點(diǎn)4處的應(yīng)力值，也即最大應(yīng)力值:

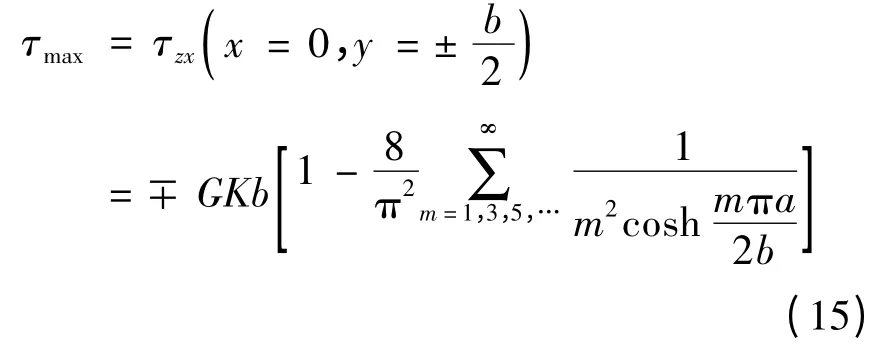
短邊的最大剪應(yīng)力發(fā)生在短邊中點(diǎn)處，令式(11)中x=±a/2，y=0，得到點(diǎn)1處和點(diǎn)2處的剪應(yīng)力值:

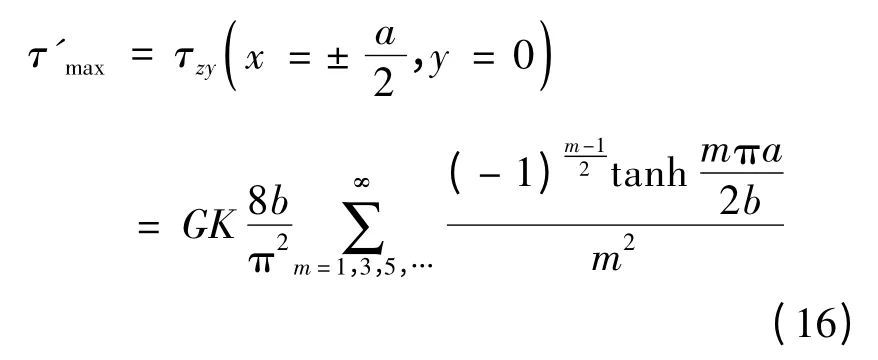
實(shí)際應(yīng)用中，記

則式(15)、式(16)簡(jiǎn)化為

則因子β1，υ1只與比值a/b有關(guān)，兩個(gè)因子的計(jì)算示例如表1所示。

表1 矩形截面構(gòu)件受純扭時(shí)的系數(shù)β1和υ1Table 1 Factorβ1 andυ1 of rectangular section members under the action of pure torsion

彈性力學(xué)的分析結(jié)果表明，矩形截面構(gòu)件在扭轉(zhuǎn)時(shí)，其橫截面上的剪應(yīng)力分布具有以下特點(diǎn):

(1)截面周邊各點(diǎn)處的剪應(yīng)力方向與周邊相切，且截面頂點(diǎn)處的剪應(yīng)力為0;

(2)最大剪應(yīng)力發(fā)生在長(zhǎng)邊中點(diǎn)處，而短邊中點(diǎn)處的剪應(yīng)力則為該邊上剪應(yīng)力的最大值;

(3)截面中心與頂點(diǎn)的連線(xiàn)上，剪應(yīng)力先增大后減小。

剪應(yīng)力分布如圖4所示［14］，最大剪應(yīng)力τmax和短邊中點(diǎn)處剪應(yīng)力可根據(jù)式(19)、式(20)計(jì)算得到。

3.3 均質(zhì)材料矩形截面構(gòu)件在剪力作用下的剪應(yīng)力表達(dá)式

材料力學(xué)中的剪應(yīng)力公式適用于狹長(zhǎng)矩形截面構(gòu)件，當(dāng)不滿(mǎn)足這一條件時(shí)，用于推導(dǎo)剪應(yīng)力公式的兩個(gè)假設(shè)不再成立(兩個(gè)假設(shè)內(nèi)容:假設(shè)矩形截面上剪應(yīng)力方向和剪力方向相同;假設(shè)截面上剪應(yīng)力沿厚度是均勻分布的)。彈性力學(xué)給出了適用于一般矩形截面構(gòu)件的剪應(yīng)力公式，受力如圖5的構(gòu)件截面的彈性力學(xué)解為［15］

圖4 矩形截面構(gòu)件受扭時(shí)剪應(yīng)力分布Fig.4 Shear stress distribution of rectangular section members subjected to torsion

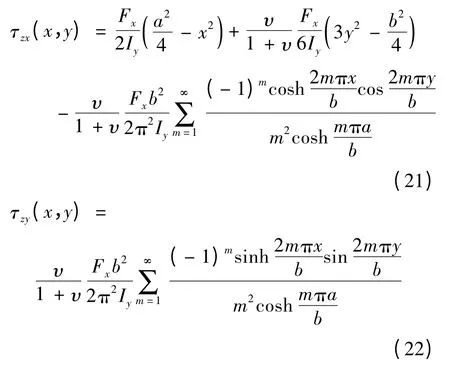
圖5 矩形截面構(gòu)件受剪Fig.5 Rectangular section members subjected to shear

式(21)第一項(xiàng)為基本部分，是狹長(zhǎng)矩形截面構(gòu)件剪應(yīng)力的解式，經(jīng)過(guò)第二、三兩項(xiàng)的修正適用于一般的矩形截面構(gòu)件。彈性力學(xué)計(jì)算表明，當(dāng)a/b≥2時(shí)，第二、三兩項(xiàng)所占比重很小，取第一項(xiàng)即可滿(mǎn)足工程精度的需要，其退化為材料力學(xué)矩形截面構(gòu)件剪應(yīng)力公式;當(dāng)不滿(mǎn)足a/b≥2時(shí)，式(21)中第二、三兩項(xiàng)所占比重不能忽略。

令式(21)中x=0，y=±b/2，得到點(diǎn)3處和點(diǎn)4處剪應(yīng)力值，即最大剪應(yīng)力值:

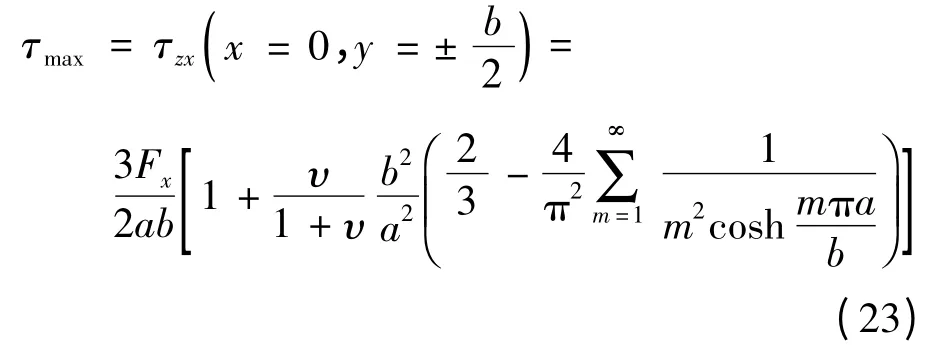
令式(22)中x=±a/2，y=0，得到點(diǎn)1處和點(diǎn)2處剪應(yīng)力值:

實(shí)際運(yùn)用中，令

則式(23)可以簡(jiǎn)化為

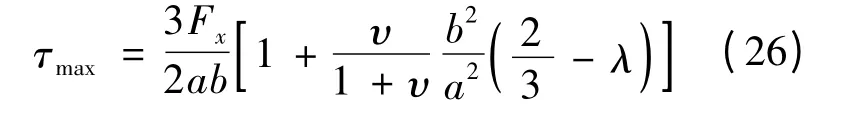
為方便應(yīng)用，將對(duì)應(yīng)于不同高寬比a/b的λ制成表格，如表2所示。

表2 矩形截面構(gòu)件剪應(yīng)力系數(shù)λTable 2 Shear stress factorλof rectangular section members

上面討論的是外力F平行于x軸的情況。當(dāng)外力F平行于y軸時(shí)，可類(lèi)似地導(dǎo)出截面內(nèi)應(yīng)力計(jì)算公式;當(dāng)外力F通過(guò)彎曲中心，但不平行于形心軸x或y時(shí)，把F沿x軸和y軸分解成Fx和Fy，分別計(jì)算兩個(gè)平面彎曲問(wèn)題，然后疊加;當(dāng)外力F不通過(guò)彎曲中心時(shí)則出現(xiàn)彎扭耦合變形，這時(shí)可先把F平移到彎曲中心上，按斜彎曲處理，然后再疊加由F對(duì)彎曲中心的力矩所引起的扭轉(zhuǎn)應(yīng)力。

3.4 鋼筋混凝土矩形截面構(gòu)件在扭矩、剪力作用下的應(yīng)力表達(dá)式

鋼筋混凝土矩形截面構(gòu)件受扭時(shí)，在彈性階段鋼筋與混凝土變形協(xié)調(diào)，整個(gè)截面的抗扭分為鋼筋抗扭和混凝土抗扭兩部分。根據(jù)勻質(zhì)材料矩形截面構(gòu)件扭矩作用下剪應(yīng)力公式(19)，扭矩作用下鋼筋混凝土矩形截面構(gòu)件在彈性階段可如式(29)的方式近似考慮鋼筋的抗扭貢獻(xiàn)。

式中，Gs為鋼筋剪切模量;Gc為混凝土剪切模量;n為鋼筋的根數(shù);τi為扭矩作用于勻質(zhì)材料矩形截面構(gòu)件時(shí)第i根鋼筋形心位置的剪應(yīng)力(以下稱(chēng)之為鋼筋的抗扭名義剪應(yīng)力);Ai為第i根鋼筋的面積;di為第i根鋼筋形心到截面形心的距離。

假設(shè)第i根鋼筋的位置(xi，yi)，此鋼筋兩個(gè)方向的抗扭名義剪應(yīng)力為τzx(xi，yi)和τzy(xi，yi)，則:

式中，τzx(xi，yi)，τzy(xi，yi)按式(10)、式(11)計(jì)算。

定義

在截面長(zhǎng)寬比確定的情況下，ηi僅與鋼筋所處的位置有關(guān)，稱(chēng)之為鋼筋的抗扭位置系數(shù)，且式(27)簡(jiǎn)化為

由勻質(zhì)材料矩形截面構(gòu)件剪力作用下剪應(yīng)力公式(26)，采用同樣方法考慮剪力作用下鋼筋混凝土矩形截面構(gòu)件鋼筋的抗剪貢獻(xiàn)，如下式所示:

式中，τi，zx為剪力作用于勻質(zhì)材料構(gòu)件時(shí)第i根鋼筋形心位置x方向的剪應(yīng)力(以下稱(chēng)為鋼筋的抗剪名義剪應(yīng)力)，按式(19)計(jì)算。

定義

在截面長(zhǎng)寬比確定的情況下，λi僅與鋼筋所處位置有關(guān)，稱(chēng)為鋼筋的抗剪位置系數(shù)，且式(32)簡(jiǎn)化為

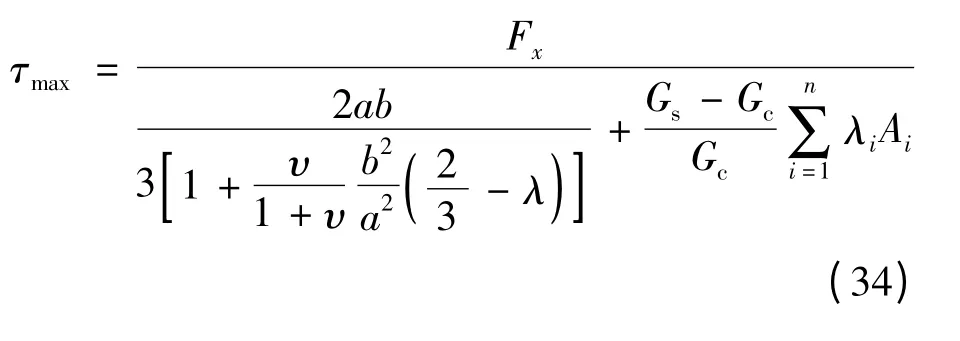
鋼筋的抗扭位置系數(shù)ηi和抗剪位置系數(shù)λi數(shù)值根據(jù)以上相關(guān)公式計(jì)算即可。例如，一個(gè)長(zhǎng)為a=500 mm、寬為b的矩形截面，鋼筋位置及編號(hào)如圖6所示，鋼筋直徑為20 mm，保護(hù)層厚度為30 mm，鋼筋的抗扭位置系數(shù)和抗剪位置系數(shù)計(jì)算結(jié)果分別見(jiàn)表3、表4。

圖6 矩形截面鋼筋位置Fig.6 Steel bar position of rectangular section members

表3 鋼筋抗扭位置系數(shù)ηiTable 3 Position factorηi of steel bar subjected to torsion

表4 鋼筋抗剪位置系數(shù)λiTable 4 Position factorλi of steel bar subjected to shear

在小變形條件下，利用疊加原理寫(xiě)出圖2截面中點(diǎn)1、2、3、4的剪應(yīng)力表達(dá)式如下:

3.5 鋼筋混凝土矩形截面構(gòu)件內(nèi)力識(shí)別

聯(lián)立式(8)、式(9)中任意三個(gè)即可求得Fz;Mx和My，如聯(lián)立前三個(gè)求得:

聯(lián)立式(35)、式(36)中任意三個(gè)即可求得Mz、Fx和Fy，如聯(lián)立前三個(gè)求得:

以上公式中的應(yīng)力由應(yīng)變花測(cè)得的應(yīng)變通過(guò)式(5)—式(7)求得;β1，υ1查表1得到，λ查表2得到，ηi查表3得到，λi查表4得到;a為矩形截面構(gòu)件的長(zhǎng)邊，b為矩形截面構(gòu)件的短邊，di，x，di，y分別為第i根鋼筋到相應(yīng)中性軸的距離。

由上面的推導(dǎo)可以看出，只要由應(yīng)力釋放法得到圖2截面上1—4點(diǎn)中任意三點(diǎn)的表面應(yīng)力，即可以計(jì)算出該截面的所有內(nèi)力分量。

4 結(jié) 語(yǔ)

介紹采用應(yīng)力釋放技術(shù)測(cè)試鋼筋混凝土構(gòu)件表面應(yīng)力的基本方法。理論推導(dǎo)了構(gòu)件截面各內(nèi)力分量作用下截面各邊中點(diǎn)處的正應(yīng)力和剪應(yīng)力，證明了只要測(cè)試出一個(gè)矩形截面三個(gè)邊中點(diǎn)處的正應(yīng)變和剪應(yīng)變值，就可以識(shí)別出截面內(nèi)力。

［1］ 劉紀(jì)軍，魯亮，王輝.應(yīng)力釋放法識(shí)別既有鋼筋混凝土構(gòu)件工作應(yīng)力的有限元分析［C］.第20屆全國(guó)結(jié)構(gòu)工程學(xué)術(shù)會(huì)議論文集Ⅰ，2011:366-371.Liu Jijun，Lu Liang，Wang Hui.Finite element analysis on the working internal forces in existing RC member by stress-release method［C］.Proceedings of the Twentieth National Conference on Structural EngineeringⅠ，2011:366-371.(in Chinese)

［2］ 劉紀(jì)軍.應(yīng)力釋放法識(shí)別既有鋼筋混凝土構(gòu)件內(nèi)力試驗(yàn)研究與分析［D］.上海:同濟(jì)大學(xué)，2012.Liu Jijun.Analytical and experimental study on internal forces measurement in existing reinforced concrete members by stress-release method［D］.Shanghai:Tongji University，2012.(in Chinese)

［3］ 時(shí)蓓玲，吳鋒，孫穆.既有混凝土結(jié)構(gòu)現(xiàn)存應(yīng)力測(cè)試方法研究［J］.水運(yùn)工程，2011，449(1):131-135.Shi Beiling，Wu Feng，Sun Mu.On the testing method for the existing stress of concrete structures［J］.Port and Waterway Engineering，2011，449(1):131-135.(in Chinese)

［4］ Mathar J.Determination of initial stresses by measuring the deformations around drilled holes［J］.Trans.ASME，1934，4:249-254.

［5］ Soete W，Van Crombrugge R.An industrial method for the determination of residual stresses［J］.Proc.SESA，1950，8(1)，17-26.

［6］ ASTM International E837 Standard test method for determining residual stresses by the hole-drilling strain gage method［S］.West Conshohocken，PA，USA:ASTM，2002.

［7］ 中國(guó)船舶工業(yè)總公司.CB 3395—92殘余應(yīng)力測(cè)試方法鉆孔應(yīng)變釋放法［S］.北京:中國(guó)標(biāo)準(zhǔn)出版社，1992.China State Shipbuilding Corporation.CB 3395—92 Residual stress determination method hole-drillingstrain-release method［S］.Beijing:Standards Press of China，1992.(in Chinese)

［8］ 翁冠群.橋梁預(yù)力損失檢測(cè)技術(shù)及安全評(píng)估［C］.2001年全國(guó)公路橋梁維修與加固技術(shù)研討會(huì)，2001.Weng Guanqun.Prestress-lossing detection technology and security assessments of bridges［C］.The highway bridge repair and strengthen technical seminar，2001.(in Chinese)

［9］ 劉永淼.環(huán)孔法測(cè)試混凝土工作應(yīng)力試驗(yàn)研究［D］.杭州:浙江大學(xué)，2006.Liu Yongmiao.Experimental research on the working stress measurement of concrete by the ring-hole method［D］.Hangzhou:Zhejiang University，2006.(in Chinese)

［10］ 宋子康，蔡文安.材料力學(xué)［M］.上海:同濟(jì)大學(xué)出版社，1998.Song Zikang，Cai Wenan.Mechanic of materials［M］.Shanghai:Tongji University Press，1998.(in Chinese)

［11］ 沈旭凱.開(kāi)槽法測(cè)試混凝土工作應(yīng)力試驗(yàn)研究［D］.杭州:浙江大學(xué)，2006.Shen Xukai.The testing and research on the working stress measurement of concrete by the grooving method［D］.Hangzhou:Zhejiang university，2006.(in Chinese)

［12］ 王柏生，沈旭凱，林湘祁.開(kāi)槽法測(cè)試混凝土工作應(yīng)力的試驗(yàn)研究［J］.浙江大學(xué)學(xué)報(bào)(工學(xué)版)，2010，44(9):1754-1759.Wang Baisheng，Shen Xukai，Lin Xiangqi.Experimental study on working stress measurement of concrete by grooving method［J］.Journal of Zhejiang University(Engineering Science)，2010，44(9):1754-1759.(in Chinese)

［13］ 徐芝綸.彈性力學(xué)［M］.北京:高等教育出版社，1990.Xu Zhilun.Elastic mechanics［M］.Beijing:Highher Education Press，1990.(in Chinese)

［14］ 殷之霖，張譽(yù)，王振東.抗扭［M］.北京:中國(guó)鐵道出版社，1990.Yin Zhilin，Zhang Yu，Wang Zhendong.Torsion［M］.Beijing:China Railway Press，1990.(in Chinese)

［15］ 陸明萬(wàn)，羅雪福.彈性理論基礎(chǔ)［M］.北京:清華大學(xué)出版社，2001.Lu Mingwan，Luo Xuefu.Basic theory of elasticity［M］.Beijing:Tsinghua University Press，2001.(in Chinese)