動目標雷達散射截面的建模研究

張晨新，莊亞強，張小寬，林存坤，王大朋

(空軍工程大學防空反導學院， 西安710051)

0 引言

目標的雷達散射截面(RCS)反映目標對照射電磁波的散射能力，是表征目標特性最基本、最重要的參數［1］。在實戰應用中，雷達目標總是處于運動狀態，因此，研究目標的動態RCS具有更高的實際價值。外場動態測量試驗是獲取動態數據必不可少的手段，世界主要軍事強國均建立了完善的外場動態測量系統［2-3］。由于外場試驗的成本高，因此，電磁計算和室內測量手段仍被廣泛采用。

目前，許多研究圍繞基于靜態數據獲取目標的動態電磁特性開展。文獻［4］根據空間目標的運動學特性，研究了彈道目標的中段動態RCS;文獻［5］考慮了氣流對飛行姿態擾動的影響，基于準靜態方法分析了運動目標的RCS特性;文獻［6］從空氣動力學原理出發，研究了靜態RCS和動態RCS在雷達檢測性能評估上的差異;文獻［7］研究了靜態數據獲取動態特性過程中的坐標變換和姿態的一致性問題。動態RCS隨姿態角劇烈起伏，通常采用起伏統計模型來描述起伏程度［8］，起伏特性將影響雷達檢測性能和雷達威力評估［9］。上述文獻的動態RCS仿真數據都沒有經過實測數據驗證，因此仿真結果的置信度值得商榷。

本文基于外場實測數據，提出了一種新的雷達目標動態RCS建模仿真方法。基于目標靜態RCS的仿真數據，采用線性插值方法獲得初步動態特性，并利用正態分布隨機數進行了修正;從而疊加了姿態擾動的影響，修正后的數據域實測數據的幅度起伏特性吻合得很好。

1 目標靜態RCS計算

1.1 復雜目標幾何建模

隨著計算機輔助設計(CAD)技術的發展，許多成熟的造型軟件可以利用不同的曲面造型方法對目標的幾何形狀進行精細化描述。本文將目標尺寸數據導入CAD軟件實現精確幾何建模，再導出為電磁仿真軟件要求的格式類型，并對模型進行修正和校驗，使之滿足電磁計算的要求。利用上述方法建立的目標模型如圖1所示。

圖1 目標模型

1.2 靜態RCS計算

將目標模型導入電磁仿真計算FEKO中進行仿真計算，仿真條件設定與測量條件一致，頻率位于C波段，垂直極化。目標坐標系定義如圖1所示，原點位于目標質心，Xb軸平行于機身縱軸指向機頭，Zb軸位于機身對稱平面內，垂直于Xb軸向上，Yb軸垂直于目標對稱平面，指向由右手法則確定。方位角φ為雷達視線在XbOYb平面的投影與OXb軸的夾角，φ的取值范圍為［0°，360°］。俯仰角θ為雷達視線在XbOZb平面的投影與OXb軸的夾角，向上為正，θ的取值范圍為［-90°，90°］。為了節省仿真計算時間，本文根據后文中將用到的飛行航跡，只計算了覆蓋該軌跡的雷達視線姿態角范圍的局部空域靜態RCS。采用物理光學法(PO)法進行計算，角度掃描步進取0.1°，因此，最后得到的局部空域靜態RCS數據如圖2所示。對于非合作目標，可將建立全空域靜態RCS數據庫作為一項基礎數據工程，便于在雷達系統仿真和目標識別時進行實時調用。

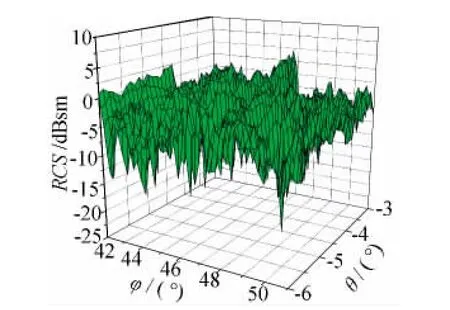
圖2 局部空域的靜態RCS數據

2 動態RCS的仿真

2.1 姿態角解算

在已知靜態數據的基礎上，根據雷達視線在機體坐標系中的方位角和俯仰角信息即可獲得目標的動態數據。目標的飛行航跡可由一般的測量雷達獲得，經過坐標變換可得雷達位置在目標坐標系中的實時坐標，則雷達視線角 φ(t)和 θ(t)分別為

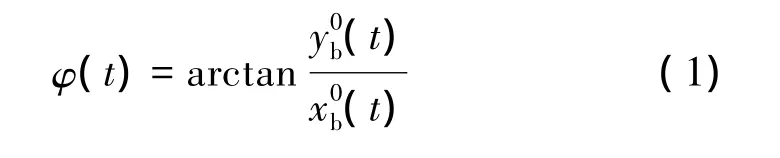
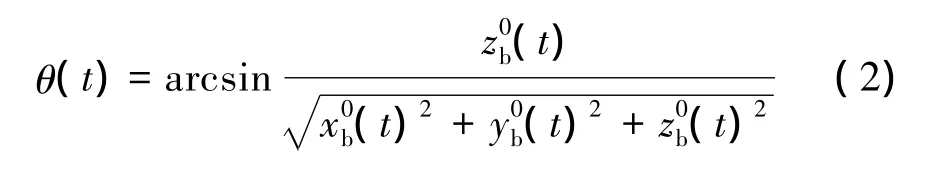
為了用實測數據驗證仿真方法的準確性，本文應用實測航跡進行姿態解算。飛行航跡為側站飛行，航跡在水平面的投影如圖3所示，距離從80 km到70 km，飛機以180 m/s的速度勻速飛行，共有1 113個采樣點。

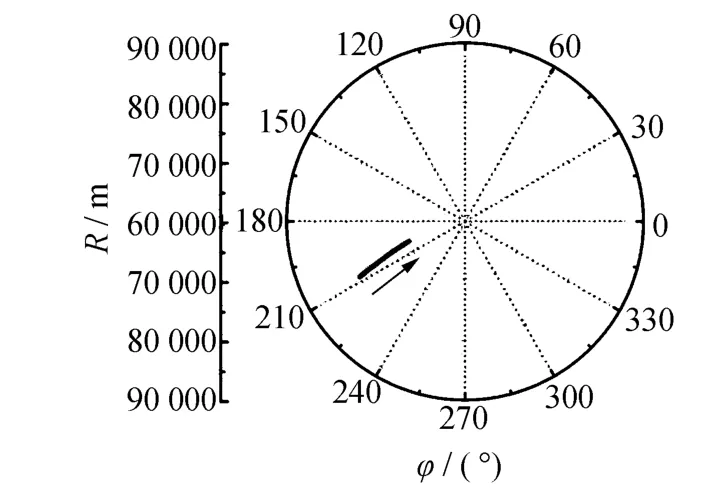
圖3 飛行航跡投影

由飛行航跡可求得雷達視線在雷達坐標系中方位角和俯仰角變化關系如圖4所示，飛行中距離一直減小，且飛行高度和航路捷徑保持不變，所以距離越小，方位角越小，俯仰角越大。經過坐標變換，可求得雷達視線在目標坐標系中的姿態角，如圖5所示，方位角變化趨勢與圖4相反。

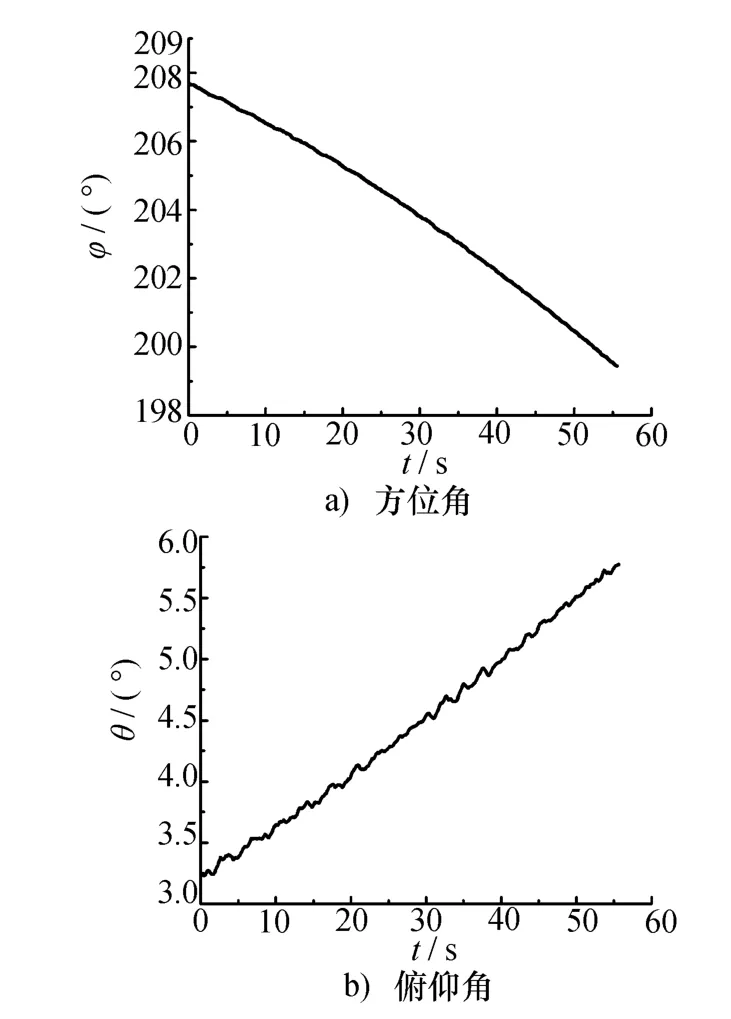
圖4 雷達坐標系中的雷達視線角

2.2 動態RCS的仿真及修正

根據雷達視線在機體坐標系中的方位角和俯仰角，在靜態RCS數據庫中提取對應的RCS值。由于數據庫的角度間隔為0.1°，因此，必然有部分姿態角的RCS值在數據庫沒有定義，本文采用線性插值法［10］計算了該部分姿態角的RCS值。由線性插值得到的動態RCS初步仿真值與實測值的比較結果如圖6所示。

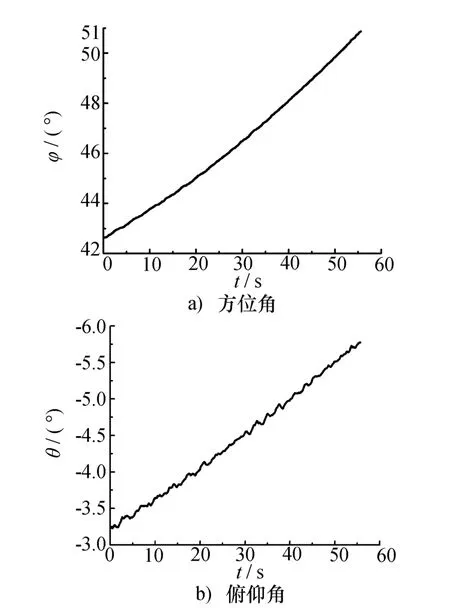
圖5 目標坐標系中的視張姿態角

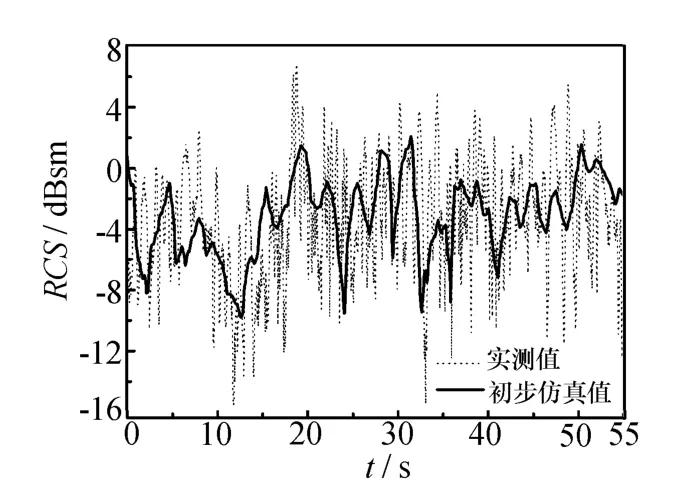
圖6 動態RCS初步仿真值和實測值比較

從圖6可以看出，雖然初步仿真值與實測值的起伏趨勢吻合得較好，但二者之間仍存在較大差距。動態數據區別于靜態數據的機理主要包括:目標運動引入的姿態角變化和上升氣流和側向風導致的飛行姿態擾動。由于初步仿真值已經考慮了前者因素的影響，因此，可以認為該差異是由飛行姿態擾動引起的。接下來，利用這種差異對初步仿真值進行修正，經過統計分析，用正態分布來擬合該項差異，如圖7所示，再用擬合參數生成隨機數對初步仿真值進行修正，修正結果如圖8所示。

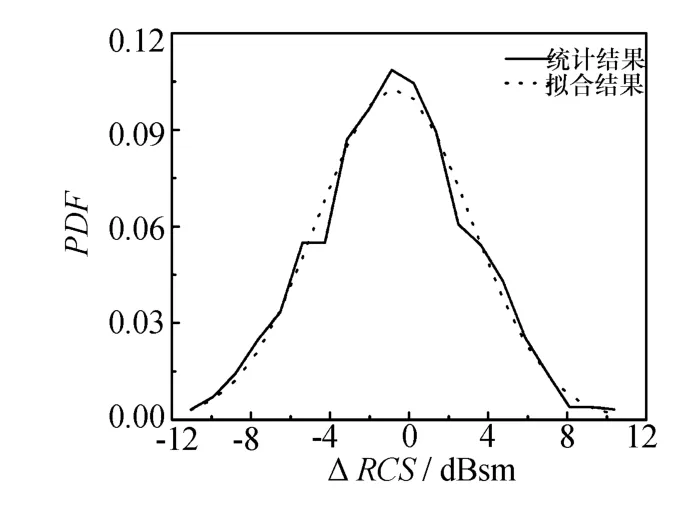
圖7 動態RCS差異分布

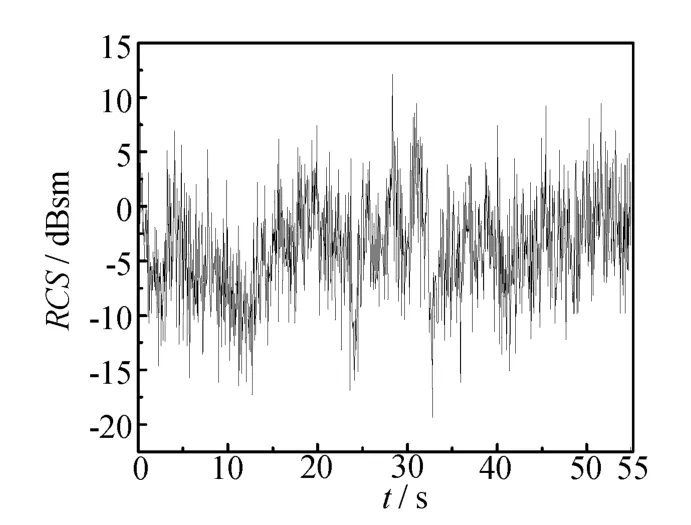
圖8 動態RCS仿真修正值

可以看出，修正結果與實測結果十分接近，但仍然有一定的差距。下面從動態測量和仿真兩個方面分析造成差距可能的原因。首先，根據RCS動態測量實施過程，認為主要由目標本身和測量系統兩個方面因素造成的。就目標本身而言，有可能是飛行控制方向舵自主轉動引起的轉動效應，也有可能是目標機動飛行機體結構變化引起的形變效應;就測量系統而言，引起測量誤差的因素主要有:定標與校準、系統穩定性、系統非線性、系統損耗、環境影響等［3］。其次，從仿真的過程看，隨機生成的正態分布隨機數將引入誤差，因為只能使隨機數服從所需的分布形式，無法確定隨機數的排序，因此，便無法確保生成的隨機數的頻譜特性也服從實際情況，故將引入偏差。上述因素對動態RCS數據的影響不大，為簡化仿真過程，故忽略其影響。

3 結果分析

3.1 RCS起伏統計模型

由于動態RCS起伏劇烈，在雷達工程領域，通常采用統計建模的方法描述RCS的起伏特性并加以應用。χ2分布模型是新一代的RCS起伏統計模型，具有通用性，包含更多的雷達目標類型［1］。其概率密度函數為

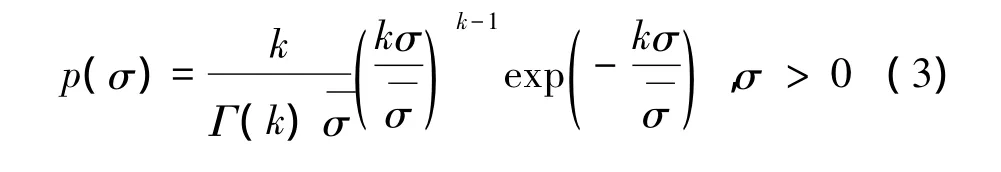
3.2 統計特性比較

為了定量比較三類動態RCS的起伏統計特性，表1給出了三者的統計參數。

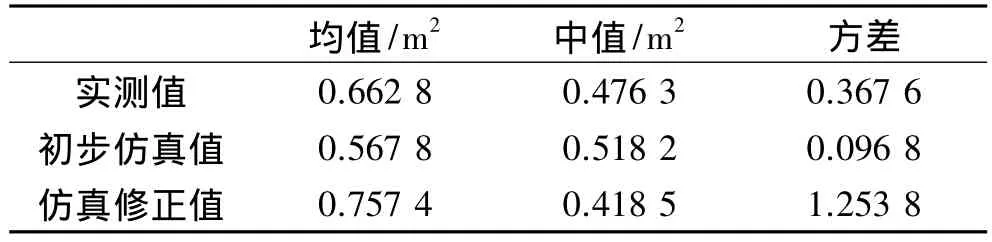
表1 統計參數比較

由表1可以看出，實測值和仿真修正值的均值和中值較為接近，但是方差相差較大，這是由仿真修正值中的個別大值和小值導致的。采用χ2分布模型對三類動態RCS進行統計建模［10］，擬合參數k和擬合誤差ef如表2所示，擬合結果如圖9所示。將誤差平方和定義為擬合誤差ef。

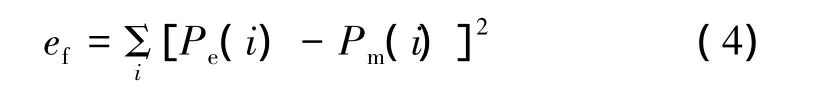
式中:Pe為RCS樣本統計分布的概率密度函數值;Pm為χ2分布模型擬合的概率密度函數值。

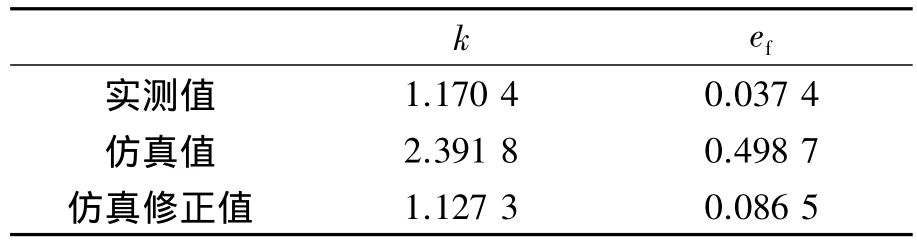
表2 擬合參數和擬合誤差

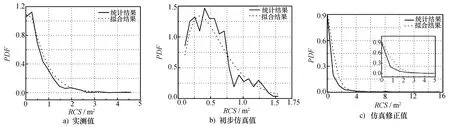
圖9 三類動態RCS結果的統計分布比較

由擬合參數和擬合結果可以得出，初步仿真值與實測值的幅度起伏特性相差甚大，而仿真修正值與實測值的幅度起伏特性吻合得相當好，分別為1.170 4和1.127 3，說明二者的起伏程度相當。雖然在仿真修正值中出現了個別大值和小值，但并不影響動態RCS的整體起伏水平，因此，可以認為仿真修正值可等效替代實測值進行應用。

4 結束語

本文提出了一種飛機目標動態RCS仿真建模的新方法。首先對目標進行幾何建模，在電磁仿真軟件中計算了目標全空域的靜態RCS數據庫。基于線性插值方法獲取目標的仿真動態RCS序列，針對飛行姿態擾動的影響，采用疊加隨機數的方法對仿真結果進行了修正。統計建模的比較結果表明:動態RCS仿真修正值與實測值的起伏特性一致，從而驗證了該仿真方法的準確性。

目標類型和運動航跡會影響飛行中姿態擾動，從而會對正態分布模型參數產生影響。探索目標和航跡類型與模型參數之間的關系，總結模型參數選取規律將是我們后續工作的重點。

［1］ 黃培康，殷紅成，許小劍.雷達目標特性［M］.北京:電子工業出版社，2005.Huang Peikang，Yin Hongcheng，Xu Xiaojian.Radar target characteristic［M］.Beijing:Publishing House of Electronics Industry，2005.

［2］ Range Commanders Council.Radar cross section(RCS)certification for static and dynamic RCS measurement capability［R］.ADA392116，New Mexio:Secretariat Range Coumanders Council U.S.Army White Sands Missile Range，2001.

［3］ 楊 濤，林 剛.飛機RCS動態測量的關鍵技術分析［J］.現代雷達，2011，33(7):75-78.Yang Tao，Lin Gang.Analysis of aircraft＇s RCS dynamic measurement technology［J］.Modern Radar，2011，33(7):75-78.

［4］ 張居鳳，馮德軍，王雪松，等.雷達目標動態RCS仿真研究［J］.系統仿真學報，2005，17(4):834-837.Zhang Jufeng，Feng Dejun，Wang Xuesong，et al.Simulation of dynamic RCS data of radar targets［J］.Journal of System Simulation，2005，17(4):834-837.

［5］ 蘇東林，曾國奇，劉 焱，等.運動目標RCS特性分析［J］.北京航空航天大學學報，2006，32(12):1413-1417.Su Donglin，Zeng Guoqi，Liu Yan，et al.RCS study of moving radar targets［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32(12):1413-1417.

［6］ 戴 崇，徐振海，肖順平.雷達目標動靜態RCS特性差異分析［J］.信號處理，2013，29(9):1256-1263.Dai Chong，Xu Zhenhai，Xiao Shunping.Analysis for differences between dynamic and static RCS characteristics of radar target［J］.Journal of Signal Processing，2013，29(9):1256-1263.

［7］ 李金梁，曾勇虎，周 波，等.飛機目標靜態與動態測量的姿態一致性［J］.北京航空航天大學學報，2013，39(4):453-457.Li Jinliang，Zeng Yonghu，Zhou bo，et al.Gesture consistency of airplane target between static and dynamic measurement［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(4):453-457.

［8］ Shi W Q，Shi X W，Xu L.Radar cross section(RCS)statistical characterization using Weibull distribution［J］.Microwave and Optical Technology Letters，2013，55(6):1355-1358.

［9］ 楊英科，李 宏，李文臣，等.目標起伏特性對雷達檢飛試驗的影響及應用［J］.現代雷達，2013，35(2):22-25，30.Yang Yingke，Li Hong，Li Wenchen，et al.Influence and application of target movement characteristic on radar flight test［J］.Modern Radar，2013，35(2):22-25，30.

［10］ 周 品.MATLAB概率與數理統計［M］.北京:清華大學出版社，2012.Zhou Pin.MATLAB probability and mathematical statistics［M］.Beijing:Tsinghua University Press，2012.