Li2MSiO4(M = Mn,Fe,Co)力學性能對電化學特性的影響 *
鄭壽紅,李 偉,姜茗浩,閆小童,侯育花,陶小馬
(1. 南昌航空大學 材料科學與工程學院,南昌 330063; 2. 廣西大學 物理科學與工程技術學院,廣西 南寧 530004)
0 引 言
能源作為人類生產生活的基石與保障,是社會繁榮與發展的重要推動力。然而隨著人口數量、能源消耗的增加以及化石燃料的枯竭和生存環境的日益惡化,迫使人們不斷發展新型能源材料及儲能材料[1]。鋰離子電池因具備較高的工作電壓、能量密度、輸出功率以及對環境友好等特點[2]而受到廣泛關注。自從Sony公司上個世紀九十年代,首次將LiCoO2作為正極材料的鋰離子電池成功商業化之后,鋰離子電池進入了飛速發展的時期。緊接著以尖晶石型LiMn2O4、橄欖石型LiFePO4和硅酸鹽類Li2FeSiO4等作為正極材料的鋰離子電池也相繼被發明與應用[3-4]。其中硅酸鹽類正極材料Li2MSiO4(M = Mn, Fe, Co)因為具有高放電比容量(理論比容量高達330 mAh/g)[5]、主體結構穩定性(具有穩定的Si-O共價鍵)[6]等特點而受到廣泛關注。
然而,硅酸鹽類正極材料Li2MSiO4(M = Mn,Fe,Co)在電化學特性和循環穩定性等方面的不足限制了其進一步發展。Dominko等[5]采用溶液-凝膠法合成了Li2MnSiO4正極材料,其最大的特點就是具備高的理論放電比容量(高達330 mAh/g),但是較差的導電特性和循環穩定性限制了其發展。研究表明Li2MnSiO4具有較差的循環穩定性主要歸因于脫鋰過程中非晶化現象的發生[7]以及Mn3+/4+離子的Jahn-Teller效應[8]。對于Li2FeSiO4正極材料,其最大特點是具備較好的循環穩定性,但是其實際放電比容量在首次充放電循環時只有165 mAh/g,并最終穩定在140 mAh/g[9],這與理論放電比容量330 mAh/g相差較大,較大程度上限制了Li2FeSiO4成為高性能鋰離子電池正極材料。此外,Li2CoSiO4正極材料因其較高的充放電平臺導致現有的電解液無法滿足其使用要求以及較差的循環特性也使得其應用受到限制[3]。
研究者們從實驗和理論的角度出發,對硅酸鹽類正極材料Li2MSiO4(M = Mn,Fe,Co)的性能改善和機理研究均做了大量工作[10-13],由于實驗條件的影響,對Li2MSiO4(M = Mn,Fe,Co)的力學性能研究是鮮有報道,而力學性能的優異與否將對正極材料的各項性能產生非常重要的影響,因此對正極材料各項力學性能參數的研究是非常有必要的。本文運用基于密度泛函理論框架下的第一性原理計算方法,嘗試計算了硅酸鹽正極材料Li2MSiO4(M = Mn, Fe, Co)的彈性常數Cij、體積模量B、剪切模量G、泊松比ν、楊氏模量E以及德拜溫度θD等參數,在一定程度上對Li2MSiO4(M = Mn,Fe,Co)體系力學性能對其電化學特性的影響進行了預測與分析。
1 計算方法與模型
1.1 計算方法
本文采用VASP(Vienna Ab initio Simulation Package)軟件包作為主要的計算軟件[14],并運用以密度泛函理論為基礎的投影綴加波法projector augmented wave(PAW)進行計算[15]。截斷能取值經過測試選取500 eV,用Monkhorst-Pack方法生成9×9×9的布里淵區K點網格。交換關聯近似則選取廣義梯度近似Generalized Gradient Approximation(GGA)條件下的Perdew-Burke-Ernzerhof(PBE)泛函[16]。自洽過程中電子的能量收斂標準為1.0×10-6eV,且原子間的相互作用力不大于0.01 eV/0.1 nm。此外,因為過渡族金屬M(M = Mn,Fe,Co)3d軌道電子間的強關聯相互作用,本文為提高計算的準確性,加入了Hubbard參數Ueff進行修正[17]。在GGA+U條件下,經過測試不同Ueff值條件下理論平均脫嵌電壓與實際放電平臺之間的關系,過渡族金屬Mn、Fe和Co的Ueff值分別選取4.5、4和5.5 eV,其具體測試結果如圖1所示。

圖1 不同Ueff值條件下理論平均脫嵌電壓與實際放電平臺之間的關系Fig 1 The relationship between theoretical averagedeintercalation voltages and actual discharge platforms under different Ueff values
1.2 計算模型


圖2 (a)Li2MSiO4(M = Mn,Fe,Co)晶胞結構;(b)相應的超胞結構Fig 2 Crystal cell structure of Li2MSiO4 (M = Mn, Fe, Co) and the corresponding supercell
2 結果與討論
2.1 結構分析
本文在GGA+U的計算條件下,計算得出了Li2MSiO4(M = Mn,Fe,Co)體系的具體晶胞參數,如表1所示。計算所獲得的晶胞參數與實驗值符合較好,表明本文所采用的GGA+U算法符合該體系。此外,通過分析比較計算理論值和實驗值可知, Li2MnSiO4擁有最大的晶胞體積,其次分別為Li2FeSiO4與Li2CoSiO4,這種晶胞體積的變化趨勢一定程度上取決于M(M = Mn,Fe,Co)的原子半徑大小。

表1 Li2MSiO4(M = Mn,Fe,Co)的晶胞參數
2.2 理論平均放電電壓分析
通過計算脫鋰前后正極材料反應物與生成物的基態能量差值,便可得出相應的理論平均脫嵌電壓[10],其計算公式如下所示:

(1)
式中Ecoh[Lix1Host]與Ecoh[Lix2Host]分別代表脫鋰前后體系的晶胞能量,Ecoh[Li]表示BCC結構Li單質的晶胞能量,x1與x2分別表示脫鋰前后晶胞中Li+的濃度。計算得出Li2MSiO4(M = Mn,Fe,Co)的理論平均脫嵌電壓如圖3所示。

圖3 Li2MSiO4(M = Mn,Fe,Co)的理論平均脫嵌電壓Fig 3 Average deintercalation voltages of Li2MSiO4 (R = Mn, Fe, Co)
由圖3可知,Li2MnSiO4,Li2FeSiO4與Li2CoSiO4單位公式內第一個Li+脫嵌時的理論平均電壓分別為4.1,3.11與4.17 V,與實驗結果一致[7,9,18]。此外,分析圖3中數據可知,對于Li2MnSiO4體系,與Li2MSiO4(M = Fe,Co)相比,其一次脫鋰與二次脫鋰之間的理論平均脫嵌電壓差值最小為0.36 V。對于Li2FeSiO4體系,與Li2MSiO4(M = Mn,Co)相比,雖然其一次脫鋰時的理論平均電壓最低,但是其一次脫鋰與二次脫鋰之間的理論平均脫嵌電壓差值卻最高為1.76 V,這主要歸因于Li2FeSiO4一次脫鋰時,Fe離子將由+2價氧化至+3價,相應的其3d軌道的電子排布也由3d6變為更為穩定的3d5半滿結構,這一過程僅需要較少的能量。而當體系進行二次脫鋰時,Fe離子將由+3價氧化至+4價,其3d軌道的電子排布將由穩定的半滿結構排布3d5向不穩定的3d4排布轉變,這一過程將需要較高的能量,因此對于Li2FeSiO4正極材料來說,使其完全脫鋰是十分困難的[19]。而對于Li2CoSiO4體系,與Li2MSiO4(M = Mn,Fe)相比,在整個脫鋰過程中其理論平均脫嵌電壓均為最高值,其原因之一是Co2+對其3d軌道電子的強烈束縛作用[20]。
此外,為了更好的厘清Li2MSiO4(M = Mn,Fe,Co)的電化學特性,本文還計算了Li2MSiO4(M = Mn,Fe,Co)的理論放電比容量及其能量密度,其具體的計算數值如表2所示。

表2 Li2MSiO4(M = Mn,Fe,Co)的理論放電比容量及能量密度
分析表2中數據可知,Li2MSiO4(M = Mn,Fe,Co)的理論放電比容量依次降低,其主要原因是Mn、Fe和Co的相對原子質量是依次遞增的進而使得體系的理論放電比容量呈現出不斷下降的趨勢。此外,分析表2中的能量密度參數可知,Li2FeSiO4表現出最低的能量密度,而Li2CoSiO4卻表現出最高的能量密度,這主要是因為正極材料的能量密度主要由體系的理論平均放電平臺與理論放電比容量共同決定,因此Li2FeSiO4(Li2CoSiO4)所表現出最低(最高)的理論平均脫嵌電壓,對體系的能量密度產生了影響。
2.3 力學性能分析
為了厘清Li2MSiO4(M = Mn,Fe,Co)體系的力學性能,本文采用應力-應變法[3],對Li2MSiO4(M = Mn,Fe,Co)體系的彈性常數矩陣[Cij]進行了計算,其具體數值如表3至表5所示。

表3 Li2MnSiO4的彈性常數

表4 Li2FeSiO4的彈性常數
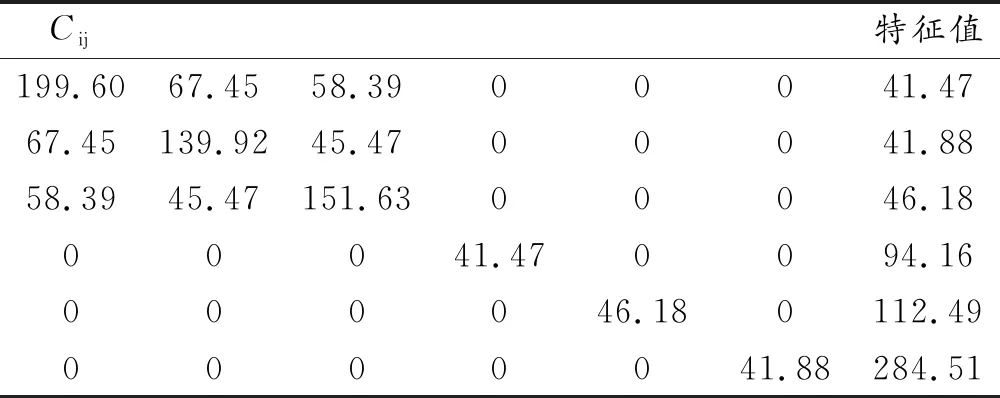
表5 Li2CoSiO4的彈性常數
由表3至表5中的特征值可知,Li2MSiO4(M = Mn,Fe,Co)體系的特征值均為正,表明Li2MSiO4(M = Mn,Fe,Co)體系的晶體結構是穩定存在的[21]。根據表3至表5中的彈性常數矩陣[Cij],本文采用Voigt-Reuss-Hill近似的方法[22-24],運用公式(2)至(14),對Li2MSiO4(M = Mn,Fe,Co)體系的體積模量B、剪切模量G、模量比B/G、泊松比ν、楊氏模量E和德拜溫度θD等進行詳細計算。具體的力學性能參數如表6所示。

表6 Li2MSiO4(M = Mn,Fe,Co)的體積模量B、剪切模量G、模量比B/G、泊松比ν、楊氏模量E和德拜溫度θD
9BV=(c11+c22+c33)+2(c12+c23+c31)
(2)
15GV=(c11+c22+c33)-(c12+c23+c31)+3(c44+c55+c66)
(3)
BR=1/[(s11+s22+s33)+2(s12+s23+s31)]
(4)
GR=15/[4(s11+s22+s33)-4(s12+s23+s31)+3(s44+s55+s66)
(5)
[S]=[C]*/│C│
(6)
公式(2)至(6)中的BV、GV是根據Voigt理論獲得,而BR與GR則是根據Reuss理論獲得。Hill認為根據Voigt與Reuss理論計算獲得的結果可以看做體系模量的上下限,所以其提出用算術平均值來表示體系的體積模量B與剪切模量G,具體公式如(7)和(8)所示。公式(6)中的[S]為相應體系的柔順系數,其具體數值是對相應體系的彈性常數矩陣[Cij]取逆來獲得。
B=(BV+BR)/2
(7)
G=(GV+GR)/2
(8)
公式(9)與(10)是計算體系泊松比ν與楊氏模量E的具體公式。
ν=(3B-2G)/[2(3B+G)]
(9)
E=9BG/(3B+G)
(10)
公式(11)為計算體系德拜溫度θD的具體公式. 公式(11)至(14)中的?為普朗克常數,kB為玻爾茲曼常數,vm為平均聲速,vt為橫向聲速,vl為縱向聲速,ρ為體系的密度。
θD=(?/kB)(3n/4πV)1/3νm
(11)
(12)
νt=(G/ρ)1/2
(13)
νl=[(3B+4G)/3ρ]1/2
(14)
模量比B/G的引入是為了對材料的延展性進行評估。其數值高(低)值與體系的韌性(脆性)有關,評判材料韌性或脆性的經驗標準數值為1.75[23]。由表6可知,Li2MSiO4(M = Mn,Fe,Co)的B/G值分別為1.97,2.19和1.94,表明Li2MSiO4(M = Mn,Fe,Co)體系均表現出良好的韌性,特別是Li2FeSiO4的B/G值最高,表現出最好的延展特性。類似的,泊松比ν也是判斷材料延展性的重要指標,其評判標準約為0.3[24],根據計算所得的泊松比ν可知,Li2MSiO4(M = Mn,Fe,Co)體系也均表現出良好的力學性能,與模量比B/G的比較結果相似,Li2FeSiO4也表現出最優的延展性特性。通過分析模量比B/G和泊松比ν可知,在Li2MSiO4(M = Mn,Fe,Co)體系中Li2FeSiO4具有最佳的力學性能,這與Li2FeSiO4具備良好循環穩定性的實驗報道是相符的[9]。此外,楊氏模量E的大小和德拜溫度θD的高低,則在一定程度上體現著體系原子之間相互作用力的大小。理論上楊氏模量E和德拜溫度θD數值越小,其原子之間的相互作用力就越小,這對正極材料來說,將有助于Li+的脫離[23]。由表6可知,Li2FeSiO4與Li2CoSiO4分別具備最小(最大)的楊氏模量E和德拜溫度θD,這與文獻中報道的Li2FeSiO4具備最低的放電平臺,Li2CoSiO4具備最高的放電平臺且Li+難以脫離的報道是相符的[3,25]。
3 結 論
本文運用第一性原理的計算方法對Li2MSiO4(M = Mn,Fe,Co)正極材料的力學性能進行了系統的研究。研究發現,對于Li2MSiO4(M = Mn,Fe,Co)體系,其模量比B/G與泊松比ν均高于和接近其韌脆轉變臨界值,表明Li2MSiO4(M = Mn,Fe,Co)正極材料均表現出較好的延展特性,其中Li2FeSiO4正極材料的力學性能最為優異。此外通過對體系的楊氏模量E與德拜溫度θD的研究可知,Li2CoSiO4電極材料具備最高的楊氏模量E和德拜溫度θD,表明其具有較強的原子間作用力,不利于Li+的有效脫離,與已有的實驗結果符合較好。

