一種克服載波頻偏的幀同步新方法*

楊 春，吳毅凌，金 野

(北京大學信息科學技術學院，北京100871)

目前，許多通信系統采用對特定序列進行相關的方法實現幀同步。例如，在IEEE 802.11［1］WLAN(Wireless Local Area Network)中，其前導序列中的短訓練符號即可被用于采用相關的方法進行幀同步。在實際通信系統中，發射機和接收機之間存在著載波頻率偏差，而接收機只有在檢測出幀起始位置后，才能進行后續的載波頻偏估計等，因而要求幀同步算法在存在載波頻偏等干擾的情況下也能夠正常工作。

目前，對特定序列進行相關的幀同步方法大體可分為兩類，一類基于求解接收信號序列的自相關函數［2-4］，另一類基于求解接收信號序列與接收端本地序列的互相關函數。基于自相關的幀同步方法對載波頻偏等干擾具有較強的抵抗能力，但采用傳統自相關方法獲得的接收信號自相關曲線往往在峰值附近變化平緩，難以在高斯噪聲較大的情況下準確檢測出幀起始位置。為了克服這一缺點，需要設計復雜的同步序列或者對自相關結果進行復雜的二次處理等［5-6］。

基于互相關的幀同步算法具有相關曲線峰值突出的優點，能夠較好的抵抗高斯噪聲的干擾。在獲得大小相近的歸一化相關峰值的情況下，互相關方法所需的同步序列長度也僅為自相關方法的一半，能夠有效降低同步序列在幀結構中所占的比例，提高傳輸效率。而且，由于本地序列為通常為雙值(‘+1’和‘-1’)序列，互相關方法所采用的相關器可以完全由加法器構成，因而硬件資源消耗遠少于自相關方法所采用的相關器。但是，互相關方法得到的相關峰值極易受載波頻偏影響［7］。當接收信號序列存在載波頻偏時，將會在每個接收樣點符號的相位中引入一個呈線性變化的干擾，導致接收信號序列與本地序列的互相關峰值隨載波頻偏增大而減小，嚴重時甚至會減小接近于0。為了克服載波頻偏的影響，文獻［8］首先根據最大似然準則估計出載波頻偏，然后將估計結果用于計算接收信號序列和本地序列的互相關結果。文獻［9］則根據最大似然準則推導出用于檢測幀同步的檢測量計算式，其仿真結果表明，當載波頻偏與信號帶寬的比值不超過0.2時，根據文獻［9］中所述表達式計算出的檢測量基本不受載波頻偏的影響。但是，文獻［8-9］中所采用方法的運算過程均過于復雜，其消耗的硬件資源隨幀同步序列長度的增加而顯著增長，不適合應用于實際通信系統。

本文對存在載波頻偏情況下接收信號序列與本地序列互相關結果的峰值變化規律進行了分析和仿真，進而提出了一種基于分段互相關的幀同步方法。此外，還分析和仿真了分段互相關方法對相關結果歸一化的影響，并提出了將相關窗內接收信號序列總能量作為輔助檢測量的解決方案。最后，本文給出了采用分段互相關方法的幀同步模塊的硬件結構，并對載波頻偏為不同數值情況下未采用分段方法和采用分段方法得到的互相關結果峰值進行了對比仿真。

1 系統描述

對于基于互相關的幀同步算法，通常在發送端將用于幀同步的序列插入到各幀的頭部，并在接收端將原始幀同步序列作為本地序列，對其與接收信號序列進行滑動相關。如果相關結果超過預先設定的門限值，則可以判斷幀起始位置在此時相關窗起點附近，進而繼續通過小范圍內的滑動搜索找出峰值位置，并將該峰值對應的相關窗起點判決為幀起始位置。為了使接收端得到的相關曲線峰值突出，通常采用具有良好滑動相關特性的序列作為幀同步序列，例如m序列等。

此外，接收端通常將相關值的絕對值或者模值平方作為檢測量與門限值進行比較，以消除相位對比較大小這一操作的影響。考慮到計算復雜度，本文采用相關值的模值平方作為檢測量。而且，由于基于互相關的幀同步算法具有很強的抵抗高斯噪聲干擾的能力，為了便于分析，以下討論只考慮載波頻偏的影響。

設發送端插入的長度為N的幀同步序列為S={s1，s2，…，sN}，該序列同時也作為接收端幀同步的本地序列。接收端得到的接收信號為R={rk，k∈(-∞，+∞)}，則本地序列與接收信號序列的滑動互相關結果為

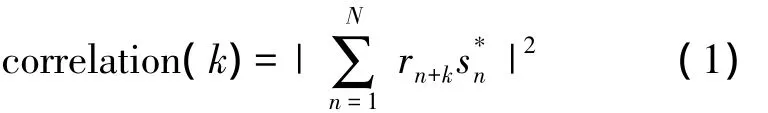
當相關窗起點恰好對應于幀起始位置時(設此時k=k0)，此時得到的互相關結果即為滑動相關結果的峰值。若載波頻偏為0，則rn+k·=1，由式(1)求出的互相關結果的峰值為N;當系統中存在的相對載波頻偏為 ε 時，rn+k·=ej2πε(n+k)，互相關結果的峰值為

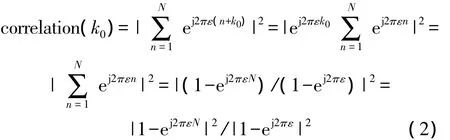
式中，ε=Δf/fband，Δf為載波頻偏，fband為信號帶寬。

由式(2)可知，在接收信號存在載波頻偏的情況下，互相關結果的峰值由N和ε共同決定。圖1(a)為N=32時互相關結果峰值與ε的關系曲線，圖1(b)為ε=0.015 6時互相關結果峰值與N的關系曲線。為了便于比較，圖1中的縱坐標為各種條件下的互相關結果峰值與無載波頻偏情況下的互相關結果峰值的比值。

由圖1(a)可知，在N一定的情況下，互相關結果峰值隨相對載波頻偏ε的增大而迅速減小，當ε的大小超過0.01時，互相關結果峰值將減小至無載波頻偏時的一半以下;由圖1(b)可知，在ε一定的情況下，互相關結果峰值隨相關窗長度N的增大而迅速減小，當ε=0.0156且N的大小超過40時，互相關結果峰值將減小至無載波頻偏時的一半以下。

在實際通信系統中，同步序列的長度為固定值。當系統中存在較大的載波頻偏時，如果采用直接對接收信號序列和本地序列進行互相關的方法檢測幀起始位置，由于相關結果峰值受載波頻偏的影響而減小，將使得漏檢概率大大增加，難以確保幀同步模塊的正常工作。

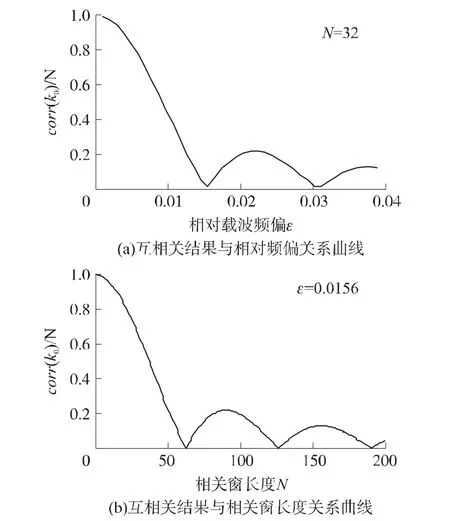
圖1 互相關結果峰值與相對頻偏和相關窗長度的關系曲線

2 現有常用幀同步方法描述

圖1(a)表明，當相關窗長度N確定時，如果使相對載波頻偏ε的數值足夠小，即可確保互相關結果峰值與無載波頻偏的情況大致相當。然而，在通信的初始階段，載波頻偏的數值是未知的。為此，可以將接收信號分為多路，每一路使用不同的載波頻偏值對其進行修正，只要其中一路修正過的接收信號的殘余載波頻偏足夠小，則可使該路接收信號序列與本地序列的相關結果峰值接近于無載波頻偏的情況［10］。

首先，設定載波頻偏的變化范圍Δfmax，并根據同步序列長度N計算出使相關結果峰值不小于幀同步判決門限Tcorr所允許的最大載波頻偏fstep/2。然后，分別以-M·fstep，-(M-1)fstep，…，-fstep，0，fstep，…，(M-1)fstep，M·fstep為預設的載波頻偏糾正值，并行對接收信號進行修正。其中，M=?Δfmax/fstep」，?」表示不小于括弧內數值的最小整數。經過頻偏糾正后各路接收信號中，必有一路接收信號殘留的載波頻偏小于fstep/2。之后，對各路接收信號序列與本地序列進行互相關運算，并選擇各路相關結果中的最大值與門限值Tcorr進行比較和判斷，從而實現幀同步。圖2為采用該方法的幀同步模塊結構框圖，圖中的比較器用于選擇各路相關結果的最大值，檢測器根據各路相關結果的最大值是否超過門限值判斷當前相關窗起點是否為幀起始位置。若檢測到幀同步位置，則輸出接收數據序列D。

由圖2可知，采用頻率掃描的方法，需要多路相關器。而且，在完成載波頻率偏差的估計和糾正之后，僅需保留其中一路用于幀同步。因此，頻率掃描的方法不僅需要消耗較多的硬件資源，而且資源利用率低下。

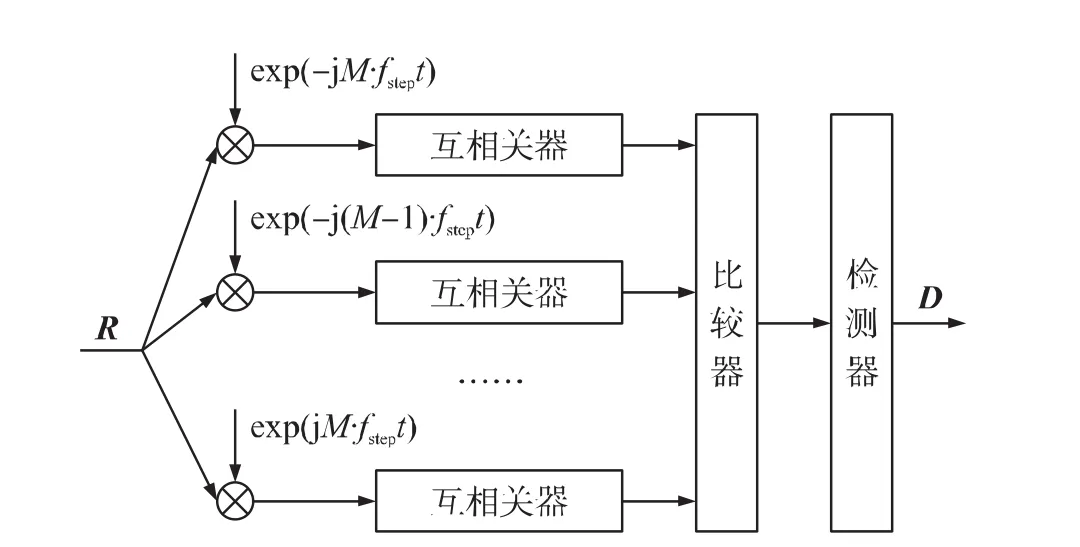
圖2 現有常用幀同步模塊結構框圖

3 基于分段互相關的幀同步方法

3.1 分段互相關方法

從另一個角度來看，在ε的大小不超過一定范圍的情況下，合理設置相關窗的大小(即N的數值)，同樣可以減小載波頻偏對相關結果的影響。本文提出的對原相關窗內的序列進行分段相關的方法，即是基于這一思想。

將原相關窗內的序列分為M段，每個分段的長度Nm≤「N/M?，分別對各分段內的接收信號子序列與本地子序列進行互相關，則第m個分段的互相關值 的 模 值 平 方 為 corrm(k)=。將各分段的互相關結果相加，得到用于檢測幀同步的相關結果

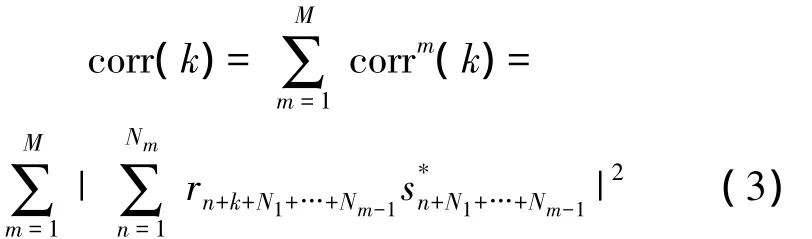
當相關窗起點恰好對應于幀起始位置時，

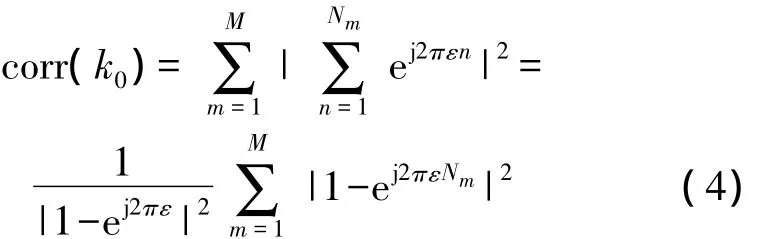
如果相關窗內的序列被等分為M段，即Nm=N/M，有載波頻偏和無載波頻偏情況下相關結果的比值為

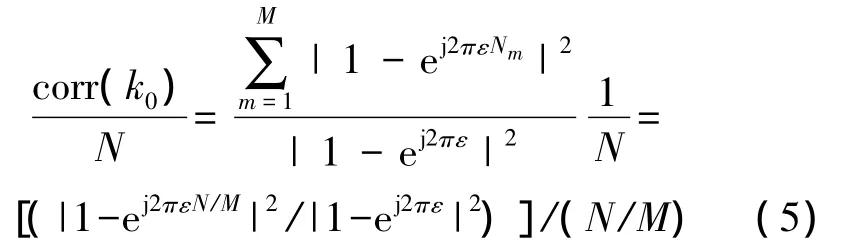
式(5)表明，采用分段相關的方法時，若相關窗內的序列被等分為M段，其等效于使總相關窗大小變為N/M。以圖1(b)所示情況為例，當ε=0.015 6時，如果要使 corr(k)/N≥80%，則N/M≤22，可得到M≥?32/22」=2，即將長度為32的相關窗等分為兩個長度為16的子相關窗進行分段相關即可確保相關結果峰值保持在無載波頻偏情況下的80%以上。

3.2 互相關結果的能量歸一化

此外，為了使相關結果不受接收信號功率的影響，通常對相關結果進行能量歸一化，即用相關結果除以相關窗內接收信號的能量總和。能量歸一化的相關結果表示為

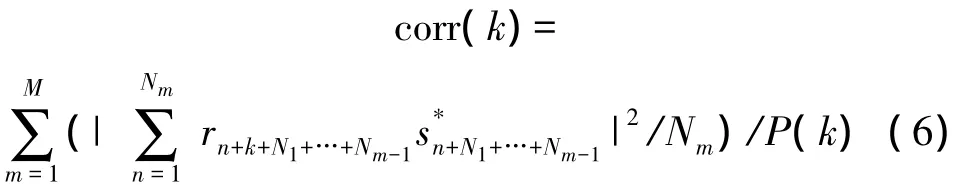
能量歸一化使得接收端可以不必根據接收信號功率調整幀同步門限值。但是，當相關窗內的接收信號全部為噪聲時，如果噪聲序列的相位恰好與本地序列相近，能量歸一化可能會使此時的相關結果超過幀同步門限值，導致幀同步出現虛警的情況。而且，分段互相關的方法使得每個子相關窗的長度遠小于原相關窗長度，使得各子相關窗內噪聲信號與本地子序列相似的可能性有所增加，從而提高了虛警概率。以幀同步序列采用長度為63的m序列為例，在信噪比為10 dB的情況下，不分段以及分斷數分別為4、8、16時幀起始位置附近的互相關結果示意圖如圖3所示。其中，橫坐標為離散序列編號，0為幀起始位置，即式(6)中的k;縱坐標為能量歸一化的相關結果，即式(6)中的corr(k)。

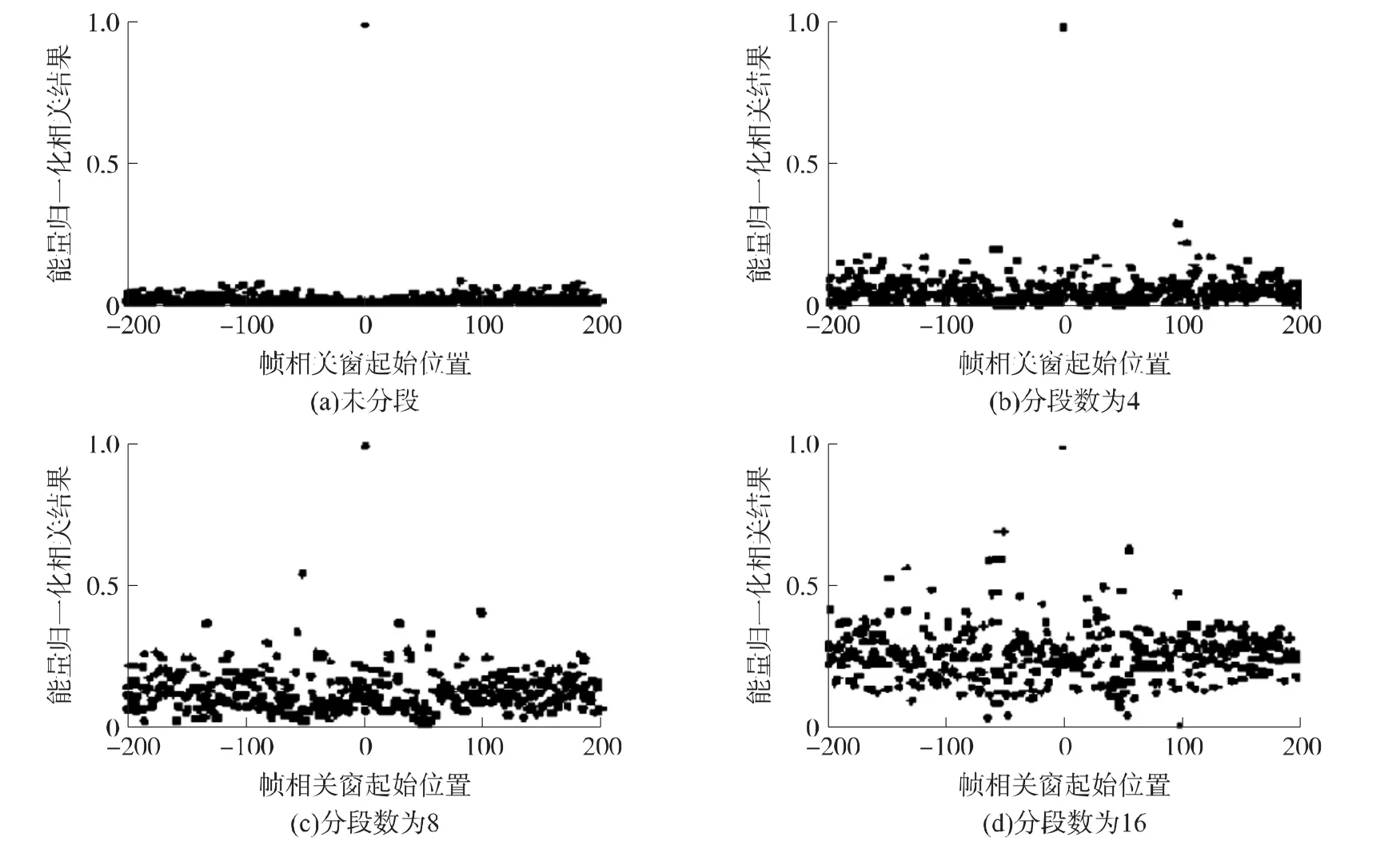
圖3 能量歸一化分段互相關結果與分段數的關系示意圖

由圖3可知，采用分段相關的方法后，隨著分段數目的增大，幀起始位置(圖中0點)之外的其他位置的相關結果數值逐漸增大，非幀起始位置的相關結果超過門限值的可能性也逐漸增大。如圖3(d)所示，當分段數目為16時，非幀起始位置處的部分相關結果甚至達到了峰值的70%。

此外，觀察圖3還可得知，在幀起始位置兩側不超過同步序列長度的范圍內，基本不會出現數值超過峰值50%的相關結果。因為此時接收信號序列的相位由發送端實際發送的信號序列相位決定，僅當相關窗起點與幀起始位置基本對準時才能使接收信號序列相位與本地序列相位相近。該結論表明，當分段數增多而導致非幀起始位置的相關結果超過門限值時，此時相關窗內的接收信號序列基本為噪聲序列，因而其序列總能量的數值較小。由此可知，使用能量歸一化相關結果作為檢測幀起始位置的判決量時，可以將相關窗內的信號能量總和是否超過功率門限值作為輔助的檢測手段，將檢測依據設為corr(k)≥Tcorr且P(k)≥Tpower，Tcorr和Tpower分別為相關結果和相關窗內信號能量總和的判決門限。在兩個不等式均滿足的條件下，再繼續進行小范圍的搜索，找出相關結果的峰值位置，峰值位置對應的相關窗起點即為幀起始位置。

綜合上述討論，使用分段互相關的方法進行幀同步時，首先需要確定相關結果的判決門限值Tcorr以及系統中可能存在的最大相對載波頻偏值εmax，由corr(k)/N≥Tcorrr+α以及式(5)確定出相關窗內序列的分段數目M，其中，α是為了防止噪聲導致相關結果減小而設置的裕度。在確定分段數目M時，盡量使M選取較小的數值，以減小分段相關導致的非幀起始位置處相關結果數值的增長。在接收端，依據盡量等分的原則將相關窗劃分為M段，并根據式(6)進行滑動分段互相關。當分段相關結果超過Tcorr時，則進一步判斷相關窗內的接收信號序列總能量P(k)是否大于Tpower:如果P(k)≥Tpower，則在小范圍內滑動搜索相關結果的峰值，并將峰值所對應的相關窗起點做為幀起始位置;否則，則認為是虛警，并繼續通過滑動分段互相關進行幀同步檢測。

3.3 硬件結構

圖4為采用不分段的互相關方法的幀同步模塊的結構示意圖。該模塊包括滑動互相關器和門限比較兩大部分。其中，主要的硬件資源消耗在互相關器中。對比圖2基于頻率掃描的同步模塊結構圖，由于圖2包含M路并行的互相關器，因此圖2中的幀同步方法的復雜度約為圖4中同步方法的M倍。

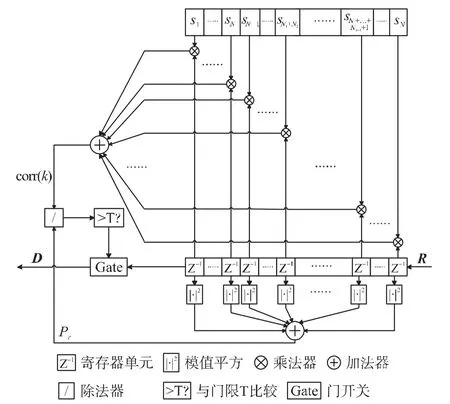
圖4 采用不分段的互相關方法的同步模塊結構圖

圖5為采用分段互相關方法的幀同步模塊結構示意圖。由圖5可知，分段互相關的方法僅需在圖4所示的滑動互相關器的基礎上增加M-1個求模值平方的單元以及M個加法單元，因而硬件資源與圖4中的方法相比沒有較大增加，其硬件資源消耗仍然約為圖2所示的頻率掃描方法所需硬件資源的1/M。而且，在完成對載波頻偏的估計和補償后，仍然可使用該相關器進行幀同步，因而其資源利用率也遠高于頻率掃描方法。

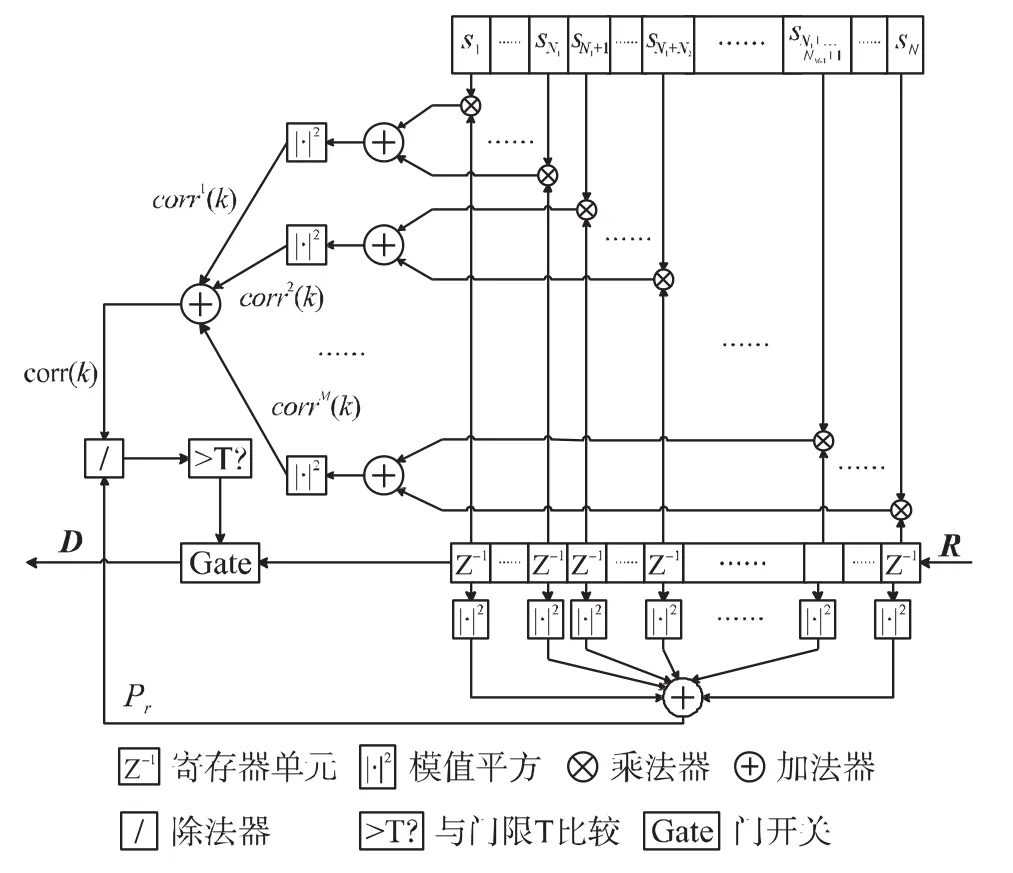
圖5 采用分段互相關方法的幀同步模塊結構圖

4 仿真結果

仿真系統以長度為63的m序列作為幀同步序列，且僅考慮載波頻偏和高斯噪聲的影響。其中，信噪比設為10 dB。

圖6為未采用分段互相關的互相關方法在ε=0、ε=0.005 2、ε=0.010 4以及 ε=0.015 6等4種情況下幀起始位置附近的相關結果示意圖，橫坐標為相關窗起始位置(0點對應于幀起始位置)，縱坐標為能量歸一化相關結果。由圖6可知，隨著ε的增大，相關結果的峰值顯著下降;當ε=0.010 4時，相關結果峰值已低于無載波頻偏情況的20%，此時已無法正常進行幀同步;而當ε=0.015 6，幀起始位置處的能量歸一化相關結果反而小于其他位置的結果。

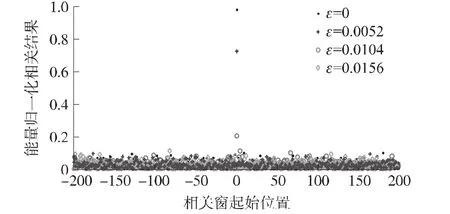
圖6 未分段互相關峰值與載波頻偏的關系示意圖

圖7為分段互相關方法在ε=0、ε=0.005 2、ε=0.010 4以及ε=0.015 6四種情況下幀起始位置附近的相關結果示意圖。相關窗內的序列被分為4段，各段的長度分別為16、16、16和15。由圖7可知，即使當ε=0.015 6時，分段互相關方法所得到的相關結果峰值仍然接近于無載波頻偏情況下的80%。仿真結果說明，分段互相關方法能夠有效抵抗載波頻偏對幀同步的影響，確保在接收信號中存在較大載波頻偏的情況下仍能正確地找到幀起始位置。

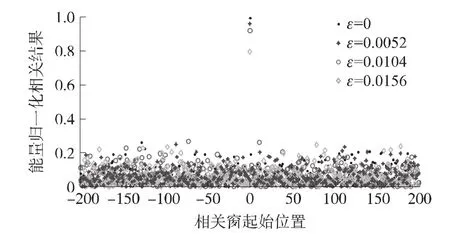
圖7 分段互相關峰值與載波頻偏的關系示意圖

5 結論

本文提出了一種基于對互相關窗進行分段的幀同步方法，該方法通過考察在存在載波頻偏情況下接收信號序列與本地序列的互相關結果峰值與相關窗長度的關系，根據系統中可能存在的最大載波頻偏確定出所需的分段數目，并按照盡量等分的原則對互相關窗進行劃分，從而有效克服載波頻偏對互相關結果峰值的影響。此外，本文還提出將相關窗內接收信號總能量作為輔助檢測量，以解決分段互相關對互相關結果歸一化的影響。本文提出的幀同步方法不僅能夠在信噪比較低且載波頻偏較大的情況下準確檢測出幀起始位置，而且實現復雜度低、硬件資源消耗小，適合于突發式通信系統幀同步模塊的實際硬件實現。

［1］IEEE 802.11—2007，IEEE Standard for Information Technology-Telecommunications and Information Exchange between Systems-Local and Metropolitan Area Networks-Specific Requirements—Part 11:Wireless LAN Medium Access Control(MAC)and Physical Layer(PHY)Specifications［S］.

［2］Tang S，Peng K，Gong K，et al.Robust Frame Synchronization for Chinese DTTB System［C］//IEEE Trans Broadcasting，2008，54:152-158.

［3］Almuzaini K K，GulliverT A.A New Time Synchronization Technique for OFDM Systems［C］//IEEE VTC.2008:1-5.

［4］Miao Shi，Yeheskel Bar-Ness，Seokhyun Yoon.A Novel Frame Synchronization Method Using Correlation between Permuted Sequences，Wireless Communications and Networking Conference，2007［C］//WCNC 2007.IEEE11-15.2007:2446-2451.

［5］羅仁澤，王汝言，朱維樂.保護帶疊加最佳訓練序列時間同步方法［J］.電子學報，2009，37(7):1584-1587.

［6］Gallardo A M，Rodriguez-Tellez J.Comparison of Joint Coarse Timing and Fine Carrier Frequency Estimation Algorithms for DVB-T of DM Based Single Frequency Networks，Vehicular Technology Conference，2002［C］//VTC Spring 2002.IEEE 55th Volume 2，6-9 May 2002.580-584.

［7］Fort A，Weijers J W，Derudder V，et al.A Performance and Complexity Comparison of Auto-Correlation and Cross-Correlation for OFDM Burst Synchronization，Acoustics，Speech，and Signal Processing，2003［C］//Proceedings.(ICASSP’03).2003 IEEE International Conference on Volume 2，6-10 April 2003.II-341-4.

［8］Younghoi Koo，Lee Y H.A Joint Maximum Likelihood Approach to Frame Synchronization in Presence of Frequency Offset［C］//Communications，2002.ICC 2002.IEEE International Conference onVolume 3，28 April-2 May 2002.1546-1550.

［9］Zae Yong Choi，Lee Y H.Frame Synchronization in the Presence of Frequency Offset，Communications［C］//IEEE Transactions on Volume 50，Issue 7，July 2002.1062-1065.

［10］劉曉明，張中山，劉元安.OFDM系統中高性能幀同步算法［J］.北京郵電大學學報，2005，28(1)，99-102.