用于語音降噪的級聯濾波器的設計與實現*

包永強

(南京工程學院通信工程學院，南京210096)

目前的一些語音信號識別系統在安靜的實驗室環境下已達到很高的性能，但在實際的帶有噪聲的環境下，由于訓練模型和識別環境的失配，系統的識別性能往往會有較大幅度的下降。為了提高語音識別系統的抗噪性，研究者提出了很多方法，除了對語音識別模型進行噪聲補償等方法外［1］，許多學者致力于研究更具魯棒性的語音特征。Hwang T H和Lee L M［2］研究了噪聲對LPC倒譜系數的影響，并對其進行噪聲補償，提高了其抗噪性。Mansour和Juang［3］提出了短時修正的相干系數 SMC(Short-Time Modified Coherence Coefficient)作為語音特征參數，Javier Hernadot［4］提出了 OSALPC(One-Sided Autocorr-elation Linear Predictive Coding)倒譜系數作為語音特征參數，它們都是基于單邊自相關函數序列的線性預測技術，實驗證明它們對加性白噪聲具有較好的抗噪性。

由于通過單一的變換很難實現語音和噪聲完全分離，1999年，Agarwal A［5］等人提出了兩級維納濾波的方法用于克服有色噪聲的干擾，獲得了很好的效果。兩級維納濾波方法的提出從某種程度上說明了采用兩種抗噪算法的系統普遍比只采用一種算法的要好，這種以復雜度換取性能飛躍的算法成為了歐洲電信標準化協會2002年10月頒布的分布式語音識別前端標準中的語音降噪的核心算法［5］。

兩級維納濾波算法的思路說明了存在著這樣一種可能——以其尋找一種復雜的變換，達到語音和噪聲的最大可能分離，不如將兩種普通的降噪算法通過某種方法結合起來，同樣可以達到很好的效果。目前國際上正展開對這方面的研究［5-6］，因此，尋找這樣一種結合方法同時又兼顧其復雜度的算法成為本章討論的主要內容。

分數階的概念最早應用于傅里葉變換中，1980年Namias V用Hermite多項式構建了分數傅里葉變換［7-8］，第一次給出了分數傅里葉變換的定義，20世紀90年代，Shih C C基于態函數重新給出了一種分數傅里葉變換的新定義［9］，Qzatkas H M［10］等人研究發現信號的冪次為α的分數傅里葉變換相當于信號在時頻面內角度απ/2的旋轉。分數傅里葉變換成為了研究熱點，在量子力學、光學、信號處理等領域內得到了廣泛的應用。

分數階理論的引入使得傅里葉變換成為分數階傅里葉變換的特例，通過改變分數階值，可使傅里葉變換的內涵得以擴展。由于傅里葉變換在信號處理領域內有著極其廣泛的應用，可以預見，分數傅里葉變換具有非常廣闊的應用前景［11］。

分數階變換的提出為兩級濾波的研究提供了一個發展方向，可以更加靈活地定義兩級維納濾波中的變換的定義。

本文把ETSI ES 202 050 V.1.1.3版本規定的Mel域上的兩級維納濾波結構推廣到分數Mel域上，提出了分數Mel域上的兩級維納濾波結構，獲得了性能的提高。

針對語音和噪聲在時域和頻域重合，而在分數余弦變換域上可能分離的特點，基于分數Mel域上的兩級維納濾波結構，提出了基于態函數的分數余弦變換域上的兩級最優濾波器;與Mel域上的兩級維納濾波結構中反復的時域-頻域轉換帶來計算量的急劇上升相比，其計算復雜度得以下降了，并且由于直接在分數余弦變換域上進行濾波，避免了由于Mel域參數較少導致的頻域不連續性帶來的時域截斷噪聲。

1 語音處理系統的DSP實現方案

系統由MIC語音輸入模塊、音頻模塊和處理模塊組成，系統框圖如圖1所示。語音信號由麥克風輸入至TLV320AIC23對語音信號進行AD轉換和濾波后，再通過DSP芯片TMS320VC5502對信號進行預處理、特征參數提取、建模及識別構成。

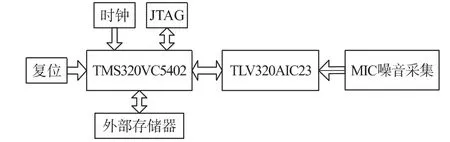
圖1 語音系統框圖

DSP芯片TMS320VC5502最高可在300 MHz主頻下工作，具有16 kbyte的緩存和17 bit×17 bit雙乘法器，并帶有32 kbit×16 bit的RAM和16 kbit×16 bit的ROM。其片上外設主要包括時鐘發生器、DMA控制器、外部存儲器接口(EMIF)、主機接口(HPI)、I2C總線、通用輸入輸出GPIO口、3個多通道緩沖串行端口(McBSP)、兩個64 bit通用定時器(GPT)和一個可編程看門狗定時器、通用異步收發器(UART)，外部尋址空間達8 Mbyte，可擴展大容量SDRAM。音頻編解碼芯片TLV320AIC23是可編程芯片，內置耳機輸出放大器，內部有11個16 bit寄存器，編程設置這些寄存器可得到所需的采樣頻率、輸入輸出增益和傳輸數據格式等。AIC23通過外圍器件對其內部寄存器進行編程配置，其配置接口支持SPI總線和I2C總線接口數據傳輸格式支持右判斷模式、左判斷模式、I2S模式和DSP模式，其中DSP模式專門針對TI公司的DSP設計。降噪算法為本文所研究的主要內容。

2 分數余弦變換域上的兩級濾波

圖2給出了在兩次濾波的示意圖，圖中白色不規則圖形的為有用信號，灰色不規則圖形為干擾信號，有用信號和干擾信號在時域和離散余弦變換(DCT)域都重疊在一起。無論從時域還是DCT域都無法簡單分離有用信號和干擾信號，除非采用復雜的方法。

從圖中可以看出，對于時域和DCT域都重疊的有用信號和干擾信號，在分數余弦變換域上，通過簡單的兩次濾波可以最大程度地消除干擾。

圖2說明了這樣一個事實，兩次簡單的變換和濾波能夠更有效地消除干擾和噪聲。對于噪聲環境下的語音信號而言，我們分析它的時域和DCT域的特性，不難發現，語音信號和干擾、噪聲無論在時域還是DCT域都是存在著重疊的可能。因此，靠一次降噪處理很難消除干擾和噪聲。

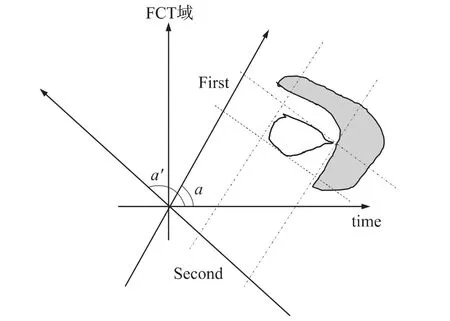
圖2 分數余弦變換(FCT)域上的兩級濾波示意圖

對于含噪語音而言，由于噪聲的非平穩性，噪聲與語音在時域和DCT域都有可能重疊，如果變換到分數余弦域上，可以最大程度地將其分開。

對于3周期的離散分數余弦變換而言

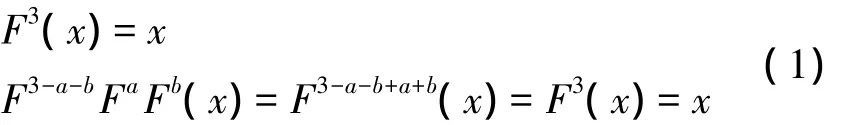
考慮到Mel域上的兩級維納濾波結構，可由兩次不同的分數階余弦變換替換其兩次傅立葉變換。具體思路如下:

首先對輸入信號進行分數離散余弦變換(FDCT)fa，然后進行濾波Ha(x);對濾波后的信號再進行分數余弦變換fb，再進行濾波Hb(x)，然后將輸出信號進行分數余弦變換f3-a-b，這樣又返回到了時域，取其實部為濾波后的輸出語音。

3 分數MEL域上的兩級維納濾波結構

分數Mel域上的兩級維納濾波沿用了ETSI ES 202 050 V.1.1.3版本規定的Mel域上的兩級維納濾波結構。與ETSI ES 202 050 V.1.1.3版本規定的Mel域上的兩級維納濾波不同的是，分數Mel域上的兩級維納濾波的頻譜估計的是獲取分數幅度譜。不同區域如圖2中的灰色部分所示。

在分數余弦變換域上，最佳線性濾波比維納濾波效果要好。無論是ETSI的Mel域上的兩級維納濾波結構還是分數Mel域上的兩級維納濾波結構，它們的結構都比較復雜，反復的時域-頻域轉換帶來計算量的急劇上升，并且不能夠避免由于Mel域參數較少導致的頻域不連續性帶來的時域截斷噪聲。

為了進一步降低計算量并提高性能，本節用最佳線性濾波器來代替維納濾波器;為了避免由于Mel域參數較少導致的頻域不連續性帶來的時域截斷噪聲，直接在分數余弦變換域上進行最優線性濾波，該方法稱為分數傅立葉域上的兩級最佳線性濾波結構TSOFF(Two Stage Optimal Filter Based on FDCT:TSOFF)。

分數余弦變換域上的兩級最佳線性濾波流程如圖3所示。

圖3 分數余弦變換域的兩級最優線性濾波的結構圖

與分數Mel域上兩級維納濾波相比，分數余弦變換域上兩級最優濾波有以下不同:

(1)采用3周期的離散分數余弦變換代替了分數傅里葉變換;

(2)相關值估計代替了頻譜估計;

(3)最優濾波代替了維納濾波;

(4)濾波直接在分數余弦變換域上進行，省去了一次傅立葉變換，從而使得結構更加簡單。

4 噪聲環境下分數余弦變換域上濾波器的性能分析

為了分析上提出的分數余弦變換域上TSMWFF、TSOFF濾波器的性能，本節針對不同噪聲環境下的語音進行分析。

在本章所有實驗中，語音數據為在實驗室內錄制的語音，采樣頻率是8 kHz，采樣位數8 bit。在純凈語音上疊加高斯白噪聲和非平穩噪聲(噪聲源由英國TNO感知學會所屬的荷蘭RSRE語音研究中心提供)。

Mel域上的兩級維納濾波在各種實際噪聲環境下可以取得良好的性能，本章將其作為基線系統，將本章提出的分數Mel域上的兩級維納濾波與之比較。

表1給出了Mel域兩級維納濾波器(TSMWF)、分數Mel域兩級維納濾波器(TSMWFF)、分數余弦變換域上的兩級最佳線性濾波(TSOFF)在高斯白噪聲(White Noise)、粉紅色噪聲(Pink Noise)、Volvo汽車噪聲(Volvo Noise)和工廠車間噪聲(Factory Noise)下的性能比較。

表1 濾波器性能比較 單位:dB

對照表1可以看出，TSOFF法最佳，TSMWFF法其次，TSMWF法最差。與 TSMWF相比，TSMWFF對pink噪聲的降噪效果要比其他噪聲要更好一些。

5 小結

本文針對語音和噪聲在時域和變換域重合，而在分數余弦變換域上可能分離的特點，把ETSI ES 202 050 V.1.1.3版本規定的Mel域上的兩級維納濾波結構推廣到分數Mel域上，提出了分數Mel域上的兩級維納濾波結構，獲得了性能的提高。

［1］Ivandro Sanches.Noise-Compensated Hidden Markov Models［J］.IEEE Trans on Speech and Audio Processing，2000，8(5):533-540.

［2］Hwang T H，Lee L M，Wang H C.Cepstral Behavior Due to Additive Noise and a Compensation Scheme for Noisy Speech Recognition［J］.IEE Proc on Vis Image Signal Process，1998，145(5):316-321.

［3］Mansour D，Juang B H.The Short-Time Modified Coherence Representation and Its Application for Noisy Speech Recognition［J］.IEEE Trans Acoust，Speech，Signal Processing，1980，28(4):357-366.

［4］Javier Hernando，Climent Nadeu.Linear Prediction of the One-Sided Autocorrelation Sequence for Noisy Speech Recognition［J］.IEEE Transactions on Speech and Audio Processing，1997，5(1):80-84.

［5］Agarwal A，Cheng Y M.Two-Stage Mel Warped Wiener Filter for RobustSpeech Recognition［C］//The 1999 International Workshop on Automatic Speech Recognition and Understanding(ASRU’99)，December，1999，Keystone，Colorado，USA.

［6］Li Jinyu，Liu Bo，Wang Renhua，et al.A Complexity Reduction of ETSI Advanced Front-End for DSR［C］//Acoustics，Speech，and Signal Processing，2004.Proceedings.(ICASSP ＇04).IEEE International Conference on Volume 1，17-21 May 2004:I-61-4.

［7］Namias V.The Fractional Order Fourier Transform and Its Application to Quantum Mechanics［J］.J Inst Math Applic，1980，25:241-265.

［8］Shih C C.Fractionalization of Fourier Transform［J］.Opt Commun，1995，118:495-498.

［9］Pei S C，Tseng C C，Yeh M H，et al.Discrete Fractional Hartley and Fourier Transforms［J］.IEEE Trans Circuit SystⅡ，1998，45:665-675.

［10］Pei S C，Yeh M H.Discrete Fractional Hadamard Transform［C］//IEEE Int Symp Circuits Syst，June 1999，1485-1488.

［11］Lohmann A W，Mendlovic D，Zalevsky Z，et al.Some Important FractionalTransformations for SignalProcessing［J］.Opt Commun，2003，125:18-20.