多參數恒Lyapunov指數譜Sprott-J系統及其數字硬件實現*

劉艷云 ，朱 雷

(1.常州紡織服裝職業技術學院機電工程系，江蘇常州213164;2.江蘇理工學院電氣信息工程學院，江蘇常州213001;3.南京航空航天大學電子信息工程學院，南京210016)

自1963年美國氣象學家Lorenz在數值實驗中偶然發現Lorenz系統以來［1］，混沌理論研究得到了長期和廣泛的關注。1999年，Chen等利用混沌反控制方法發現了與Lorenz系統相似但拓撲不等價的Chen系統［2］。2002年，Lü等發現了實現 Lorenz系統和Chen系統之間過渡的Lü系統［3］和連接上述3個系統的統一混沌系統［4］。從便于進行工程應用的角度出發，構建具有某些特殊動力學行為的混沌系統，使其產生混沌信號的幅度、相位等受系統參數控制，并呈現確定的控制規律，則易于實現參數調制或混沌鍵控，從而為混沌在通信系統中的應用奠定理論基礎，恒Lyapunov指數譜混沌系統便是這樣一類系統。2009年，Li等在一個改進Colpitts振蕩器模型［5］的基礎上，將其非線性指數項改為分段線性的絕對值項，得到一個恒Lyapunov指數譜混沌系統［6］，在3個系統參數中，有一個參數具有恒Lya-punov指數譜和局部線性調幅特性，隨后，Li進一步對系統進行了改進［7］和推廣［8］。2011 年至今，文獻［9-11］相繼報道了一些具有單參數或雙參數恒Lyapunov指數譜特性的新混沌系統，但目前尚未發現關于多參數恒Lyapunov指數譜混沌系統的報道。

1994年，美國學者Sprott在大量數值實驗的基礎上，提出了19種混沌系統，并為這些系統設置了固定的參數［12］，文獻［13］在其中的 Sprott-B 系統模型基礎上構建了一個具有調幅特性的分段線性混沌系統，本文則以Sprott-J系統作為研究對象，將其定參數改為變參數并進行巧妙的恒Lyapunov指數譜鎖定，從而得到一個多參數恒Lyapunov指數譜混沌系統。

1 系統模型

通過對Sprott-J系統進行多參數恒Lyapunov指數譜鎖定，得到如下系統:

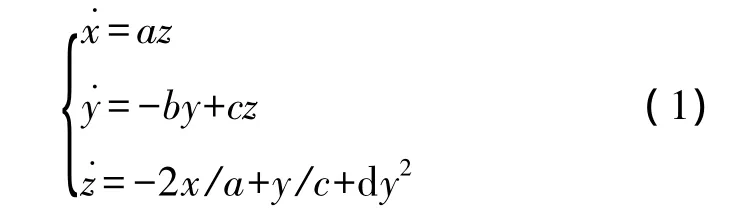
式中a，b，c，d為非零實參數，x，y，z為系統的狀態變量。當取參數a=2，b=2，c=1，d=1 時，系統(1)便成為基本Sprott-J系統，系統存在一個典型的單渦卷混沌吸引子，如圖1所示。此時系統(1)的3個Lyapunov指數為LE1=0.074，LE2=0.003，LE3=-2.076，Lyapunov維數為dL=2.037。

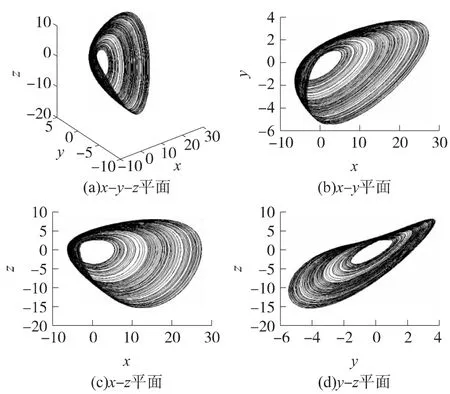
圖1 系統(1)的相軌圖(a=2，b=2，c=1，d=1)

2 動力學特性分析

2.1 基本動力學特性分析

對于系統(1)，滿足

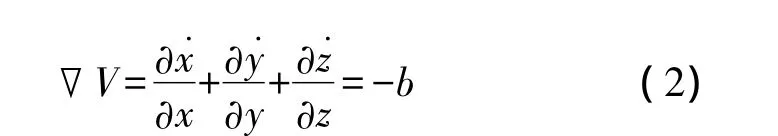
從而，當b＞0時系統(1)耗散。系統(1)的平衡點為S=(0，0，0)，在平衡點S處線性化系統(1)，得其Jacobi矩陣:

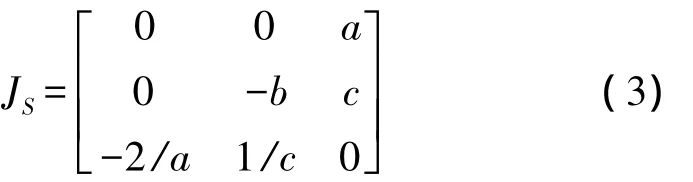
及特征多項式:

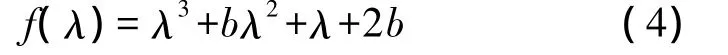
根據Routh-Hurwitz判據，對于任意實數b，平衡點S均不穩定，可能產生混沌，當a=2，b=2，c=1，d=1時，平衡點S對應的特征根為λ1=-2.314 6，λ2，3=0.157 3±1.305 2i，因此，此時平衡點S為指標2的鞍焦點。

2.2 系統參數的影響

通過觀察特征多項式(4)可以發現，其特征值與b相關，與a，c，d無關。因此，參數b的改變可能導致系統狀態的演變，而參數a，c，d不影響系統在相空間上的動力學特征。下面通過Lyapunov指數譜和分岔圖來進一步揭示參數a，b，c，d的改變對系統狀態及動力學行為的影響。

固定參數b=2，c=1，d=1，當a∈［0.1，10］時，系統(1)的Lyapunov指數譜和分岔圖如圖2所示。從圖2可見，隨著a的變化，系統的Lyapunov指數譜保持不變，此時的Lyapunov指數實質就是系統在a=2，b=2，c=1，d=1 時的 Lyapunov指數值，而隨著a的增大，系統的輸出信號x的幅度增大，y和z的幅度保持不變。

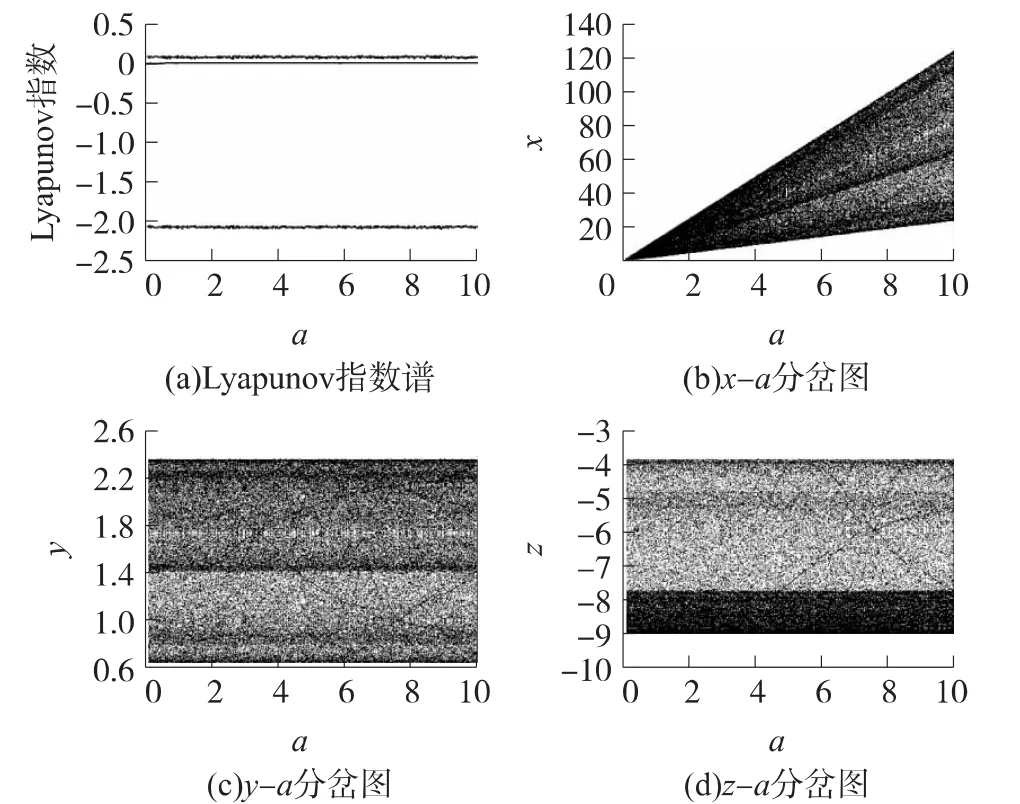
圖2 a變化時系統(1)的Lyapunov指數譜和分岔圖

固定參數a=2，c=1，d=1，當b∈［1.4，3.4］時，系統(1)的Lyapunov指數譜和分岔圖如圖3所示。從圖3可見，隨著b的改變，系統的Lyapunov指數譜發生明顯的變化并伴隨豐富而有趣的分岔模式，從而導致系統狀態在周期與混沌之間的演變。當1.4≤b＜1.58，1.708＜b＜1.86，1.928＜b＜2.056或2.056 1＜b＜2.312時，有一個正的 Lyapunov指數，系統處于混沌狀態;當1.58≤b≤1.708，1.86≤b≤1.928，2.056≤b≤2.0561 或2.312≤b≤3.4 時，最大Lyapunov指數為0，系統處于周期狀態，并且系統在b=1.688和b=1.868處分別出現倍周期分岔和反向倍周期分岔，從而由周期3狀態進入周期6狀態;在b=2.448處出現反向倍周期分岔，由周期2狀態進入周期4狀態;在b=3.02處出現反向倍周期分岔，由周期1狀態進入周期2狀態，這些周期狀態及其分岔模式的存在對系統向混沌狀態演變具有重要的作用，限于篇幅，這里僅給出兩個典型周期狀態的相軌圖，如圖4所示。

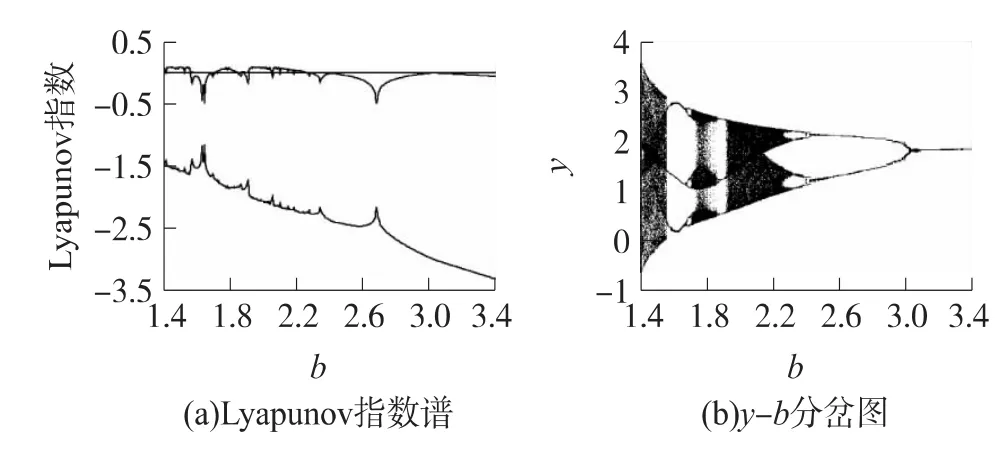
圖3 b變化時系統(1)的Lyapunov指數譜和分岔圖

圖4 系統(1)的典型周期相軌圖(a=2，c=1，d=1)

固定參數a=2，b=2，d=1，當c∈［0.2，2］時，系統(1)的Lyapunov指數譜和分岔圖如圖5所示。從圖5可見，隨著c的變化，系統的Lyapunov指數譜保持不變，即系統在a=2，b=2，c=1，d=1 時的Lyapunov指數值，而系統的輸出信號x，y和z的幅度隨著c的增大而減小。

固定參數a=2，b=2，c=1，當d∈［0.2，2］時，系統(1)的Lyapunov指數譜和分岔圖如圖6所示。從圖6可見，隨著d的變化，系統的Lyapunov指數譜保持不變，同樣等于系統在a=2，b=2，c=1，d=1時的Lyapunov指數值，而系統的輸出信號x，y和z的幅度隨著d的增大而減小。

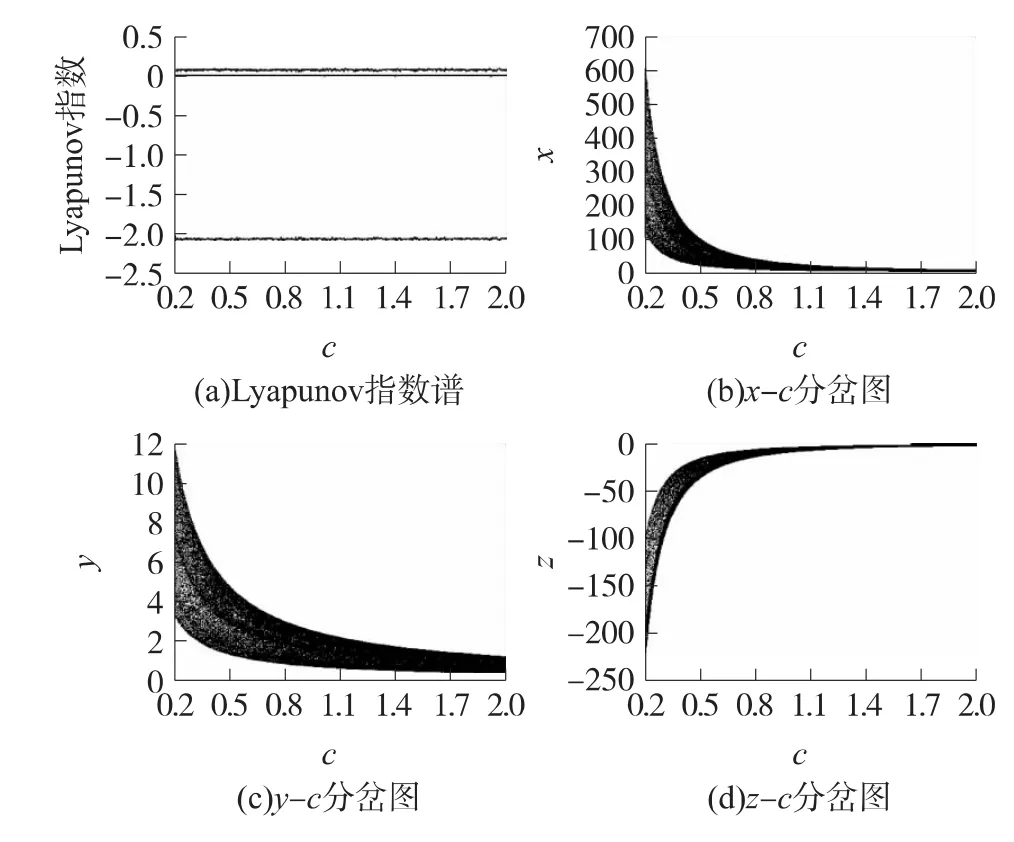
圖5 c變化時系統(1)的Lyapunov指數譜和分岔圖

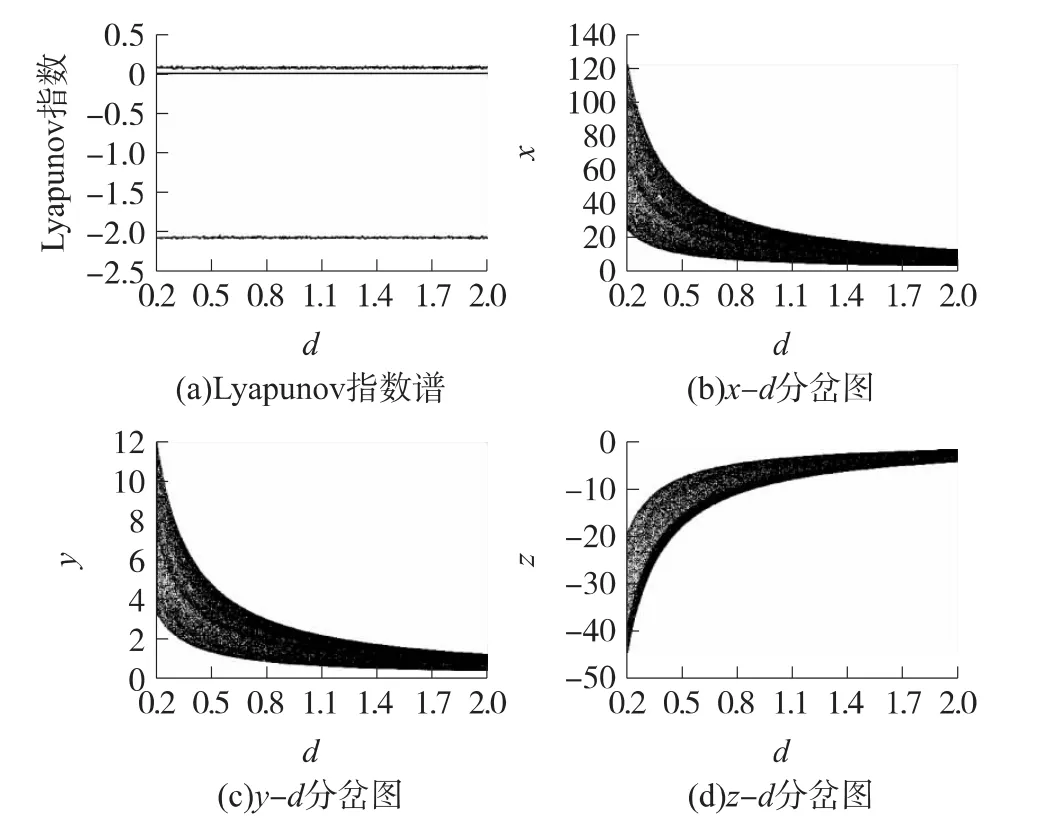
圖6 d變化時系統(1)的Lyapunov指數譜和分岔圖

2.3 多參數調幅特性分析

上述數值仿真表明參數a，c，d變化時，系統(1)輸出信號的振蕩幅度部分或全部地發生變化，參數a，c，d具有局部線性或全局非線性調幅特性。這種局部線性與全局非線性并存的多參數調幅特性為混沌應用于多參數聯合調制的復雜通信系統提供了理論基礎。

定理1系統參數a是局部線性調幅參數，輸出信號x的幅值與a呈線性關系變化，輸出信號y和z的幅值與a的變化無關。

證明令x=kx*(k≠0)，y=y*，z=z*，則系統(1)變為如下形式:

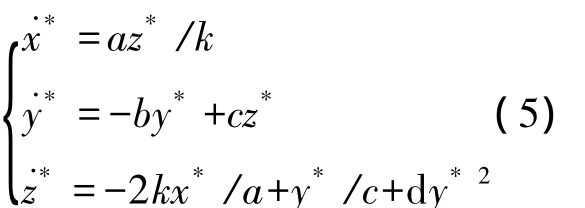
由此可知，系統(1)的狀態變量x的線性調整等價于參數a的尺度變化，參數a是局部線性調幅參數，輸出信號x的幅值與a呈線性關系變化，輸出信號y和z的幅值與a的變化無關。證畢。

定理2系統參數c是全局非線性調幅參數，輸出信號x和z的幅值與c呈冪函數關系變化，其指數為-2，輸出信號y的幅值與c也呈冪函數關系變化，其指數為-1。

證明令x=k2x*，y=ky*，z=k2z*(k≠0)，則與定理1類似可以得證，這里過程從略。

定理3系統參數d是全局非線性調幅參數，輸出信號x，y和z的幅值與d呈冪函數關系變化，其指數為-1。

證明 令x=kx*，y=ky*，z=kz*(k≠0)，則與定理1類似可以得證，這里過程從略。

3 數字硬件實現與實驗驗證

以TI公司的16bit低功耗微控制器MSP430F249為核心，結合Linear Technology公司的16 bit高速并行D/A轉換器LTC1668和TI公司的高速運算放大器OPA2690，設計出混沌系統數字實現的硬件電路，其框圖如圖7所示。MSP430F249以數字方式實現混沌信號的實時生成，LTC1668將此數字信號轉為模擬電流信號，最后由OPA2690完成電流-電壓轉換，兩路混沌電壓信號VX和VY分別被送至示波器X和Y輸入端。

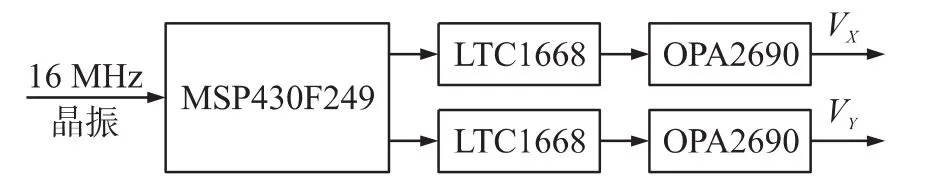
圖7 混沌系統數字實現框圖

為以數字方式實現系統(1)，須將其系統微分方程離散化為差分方程，這里采用簡單而高效的歐拉算法進行離散化處理，得到:

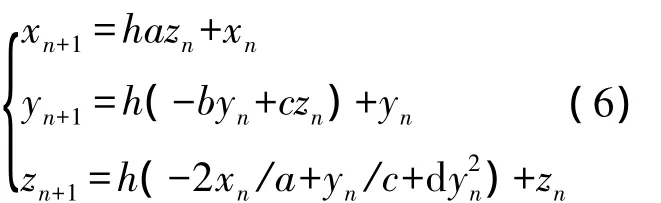
式中h為步長，n為迭代次數。

根據式(6)可以編制出基于MSP430F249的C語言程序，程序中設置h=0.001，設定參數a=2，c=1，d=1，并分別令b=2，b=1.65，b=2.4。采用具有高分辨率的安捷倫DSO7032A數字示波器對系統運行后得到的吸引子進行了實驗觀察，結果如圖8所示，與圖1、圖4對比可以發現，實驗結果與仿真結果保持一致，以數字方式完全可以實現本文所構建的多參數恒Lyapunov指數譜Sprott-J系統。

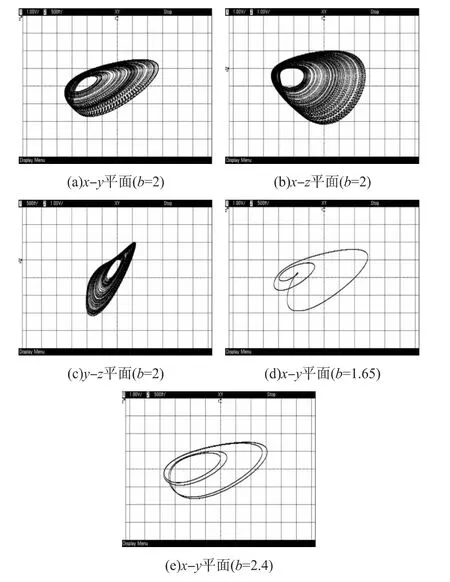
圖8 系統(1)的實驗相軌圖(a=2，c=1，d=1)

4 結論

本文在基本Sprott-J系統的基礎上，引入4個系統參數，巧妙地進行了恒Lyapunov指數譜鎖定，致使在系統特征多項式中消去3個參數，從而得到一個多參數恒Lyapunov指數譜混沌系統。采用相軌圖、Lyapunov指數譜和分岔圖等動力學手段對系統進行了數值仿真，研究結果表明，參數b可以決定系統的狀態及其演變，存在倍周期分岔和反向倍周期分岔通往混沌的道路，使系統在周期與混沌狀態之間演變，而另外3個參數a，c和d則擁有恒定的Lyapunov指數譜，從而使系統工作于魯棒混沌狀態。進一步的理論分析則揭示出這3個參數還具有局部線性或全局非線性調幅特性，因此易于實現多參數聯合調制或混沌鍵控，為混沌在復雜通信系統中的應用打下理論基礎。此外，設計了以16 bit低功耗微控制器MSP430F249為核心的數字硬件電路，在基于歐拉算法進行離散化處理的基礎上，實現并驗證了本文所構建的多參數恒Lyapunov指數譜Sprott-J系統，數字化的實現方式便于與現代數字通信和軟件無線電系統中的數字信號處理技術兼容，從而打下混沌系統應用的工程基礎。

［1］Lorenz E N.Deterministic Nonperiodic Flows［J］.Journal of the Atmospheric Sciences，1963，20(2):130-141.

［2］Chen G R，Ueta T.Yet Anthor Chaotic Attractor［J］.International Journal of Bifurcation and Chaos，1999，9(6):1465-1466.

［3］Lü J H，Chen G R.A new Chaotic Attractor Coined［J］.International Journal of Bifurcation and Chaos，2002，12(3):659-661.

［4］Lü J H，Chen G R，Cheng D Z，et al.Bridge the Gap between the Lorenz System and the Chen System［J］.International Journal of Bifurcation and Chaos，2002，12(12):2917-2926.

［5］Maggio G M，Feo O D，Kennedy M P.Nonlinear Analysis of the Colpitts Oscillator and Applications to Design［J］.IEEE Transactions on Circuits and Systems—Ⅰ:Fundamental Theory and Applications，1999，46(9):1118-1130.

［6］李春彪，王德純.一種恒Lyapunov指數譜混沌吸引子及其Jerk電路實現［J］.物理學報，2009，58(2):764-770.

［7］李春彪，陳謖，朱煥強.一個改進恒Lyapunov指數譜混沌系統的電路實現與同步控制［J］.物理學報，2009，58(4):2255-2265.

［8］李春彪，王翰康.推廣恒Lyapunov指數譜混沌系統及其演變研究［J］.物理學報，2009，58(11):7514-7524.

［9］周小勇.一種具有恒Lyapunov指數譜的混沌系統及其電路仿真［J］.物理學報，2011，60(10):100503.

［10］李春彪，徐克生，胡文.Sprott系統的恒Lyapunov指數譜混沌鎖定及其反同步［J］.物理學報，2011，60(12):120504.

［11］李春來，禹思敏，羅曉曙.一個新的混沌系統的構建與實現［J］.物理學報，2012，61(11):110502.

［12］Sprott J C.Some Simple Chaotic Flows［J］.Physical Review E，1994，50(2):647-650.

［13］朱雷，劉艷云.一個具有調幅特性的分段線性混沌系統與微控制器實現［J］.電子器件，2012，35(6):652-656.