基于模糊可拓層次分析法的訂單融資風險評價

趙 琪

(中北大學，太原 030051)

一、引言

訂單融資作為供應鏈金融服務中一種重要業務，使處于上游的供應商可以以其下游核心廠商的訂單為擔保向金融機構貸款，金融機構在物流企業的協助下審核訂單真實性并評估相應風險后對融資企業給予一定授信額度［1］。訂單融資業務已得到越來越多企業的認可，現已成為解決中小企業融資難的一種有效方式。

在目前對供應鏈金融的研究中，專家學者們多集中在應收賬款融資、動產質押融資等業務領域，如霍艷芳(2011)［2］、李澤平(2011)［3］等都對供應鏈金融服務中的應收賬款融資或動產質押融資的融資方式、風險評價進行了研究，而對訂單融資業務的研究還比較少。此外，目前對供應鏈金融風險的評價多采用傳統的層次分析法，如汪守國(2011)［4］等采用層次分析法對供應鏈金融風險進行了評價。此方法在構造判斷矩陣時沒有考慮人們判斷的模糊性，并且在不滿足一致性檢驗時需要多次調整判斷矩陣，判斷矩陣的調整有一定的盲目性。

與傳統層次分析法相比，可拓層次分析法將可拓數學和物元理論與層次分析相結合，形象描述了人判斷的模糊性，用區間數代替點值數構造判斷矩陣，將權重向量的求解與一致性檢驗結合進行，并考慮人們判斷的模糊性和多位參評專家的實踐經驗，使之自然滿足一致性條件，使得判斷矩陣更加合理。在得到各層次的權重向量后，利用模糊綜合評價法對各指標進行綜合評價，得到總體得分［5］。因此，采用可拓層次分析和模糊綜合評價相結合的方法對訂單融資風險進行評價比較恰當。

二、訂單融資風險評價指標體系的構建

本文根據訂單融資的“封閉性”、“復雜性”、“靈活性”特點［6］，并通過整理相關文獻和借鑒我國商業銀行傳統的風險評估指標體系，構建訂單融資風險評價指標體系，見表1。

三、模糊可拓層次分析法模型的構建

(一)可拓層次分析法

1.構造判斷矩陣

本文采用Saaty提出的互反性1～9標度法［7］作為可拓區間層次分析法的標量化方法。先建立層次結構，然后對處于同一層的元素進行兩兩比較，利用可拓區間數來定量表示它們的相對優劣程度，從而構造一個可拓區間數判斷矩陣A=(aij)n×n，i，j=1，2，…n，該矩陣為正互反矩陣，其中aij=［，］是一個可拓區間數，，分別為判斷矩陣第i行第j列可拓區間元素的上下端點。為了把可拓判斷矩陣中的每個元素定量化，可拓區間數的中值就是層次分析法中比較判斷所采用的1～9標度中的整數。

表1 訂單融資模式下供應鏈金融風險評價指標

2.計算綜合可拓判斷矩陣和權重矢量

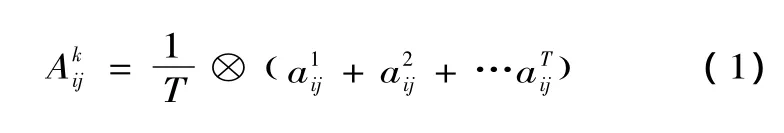
構建判斷矩陣A。在可拓區間數判斷矩陣A=［A－，A+］中，A－和 A+分別為區間上、下端點構成的矩陣。求其滿足一致性條件的權重矢量的步驟［8］為:

(1)求A+，A－的最大特征值所對應的具有正分量的歸一化特征矢量x+，x－。

式中，k，m分別為滿足0＜kx－＜mx+的全體正實數，i，j=1，2，…，nk。

(3)判斷矩陣的一致性。若0≤k≤1≤m，則說明可拓區間判斷矩陣的一致性較好。但一致性程度過低時應采取措施校正判斷矩陣或讓專家重新判斷，直到滿足要求。

(4)求出權重量。

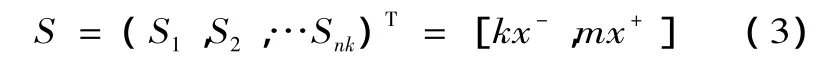
式中，Snk為第k層第n個因素對上一層次的某個因素的可拓區間權重量。

3.層次單層排序

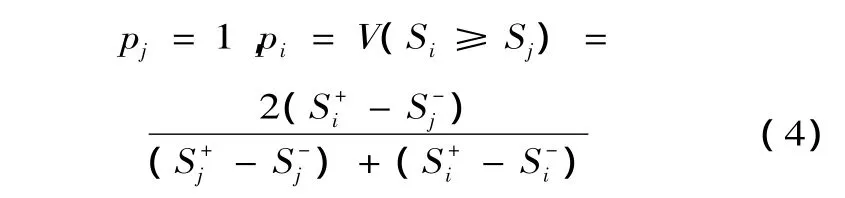
式中:i，j=1，2，…，n;i≠j，pi表示某層上第 i個因素對上一層的某個因素的單排序，經歸一化后得到的p=(p1，p2，…，pn)T表示某層上各因素對上一層的某個因素的單排序權重矢量表示2個單層權重矢量可拓區間數的上下端點。

4.層次總排序

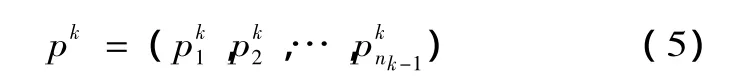
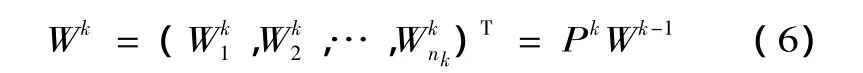
并且一般地有 Wk=PkWk－1…P3W2，式中的 W2就是單項排序矢量。

(二)模糊綜合評價法

1.確定評價因素集合

評價因素集 U={U1，U2，…，Un}是給定因素集U按不同屬性劃分為n個互不相交的集合，其中每一個一級評價指標Ui都有k個二級評價指標uij(i=1，2，…，n;j=1，2，…，k)與之對應。

2.確定評價評語集合

評價評語集合 V={Vi，V2，…，Vm}用于將定性指標量化，一般影響等級選4～8級比較合適。

3.確定隸屬度矩陣

某指標對應評語等級的隸屬度以這一指標屬于某一評語等級的人數占總人數的百分比來確定。隸屬度矩陣為

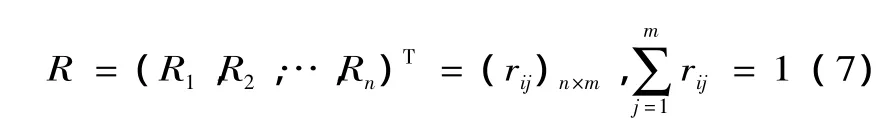
式中n為指標數，m為評價等級，rij為對第i個指標作出第j種評價等級的人數占參加評價總人數的百分比。

4.確定指標權重與隸屬度

由可拓層次分析法得到一級指標Ui對目標的權重集為 W={W1，W2，…，Wn}，n 為一級評價指標的個數。二級指標 uij(i=1，2，…，n;j=1，2，…，k)對一級指標U1的權重集為

wi={wi1，wi2，…，wij}(i=1，2，…，n;j=1，2，…，k)π。二級指標對目標的綜合權重向量為:

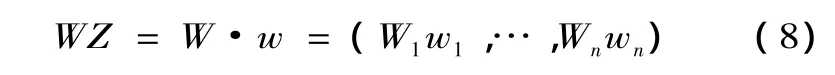
一級指標Ui內各二級指標的隸屬度為Bi=wi?Ri。由于 R=(R1，R2，…，Rn)T再按 M(?，+)模型進行合成運算，得到一級指標綜合隸屬度:

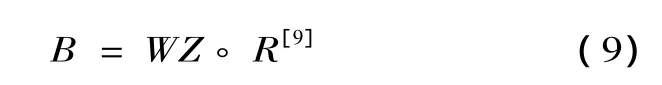
5.綜合評價結果

若用以總分數表示綜合評價結果，取評價標準的隸屬度集為(高，很高，一般，較低，低)，根據越大越好的原則［10］，可令評價集為

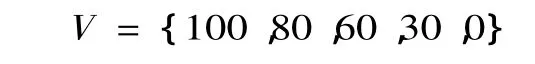
則綜合評價總分為:

四、某中小企業訂單融資業務風險評價

(一)確定各指標的相對重要度

由參加測評的專家(假設兩位)對準則層訂單融資模式下供應鏈金融風險評價中各項一級指標，進行兩者比較并打分，得到可拓區間數判斷矩陣。

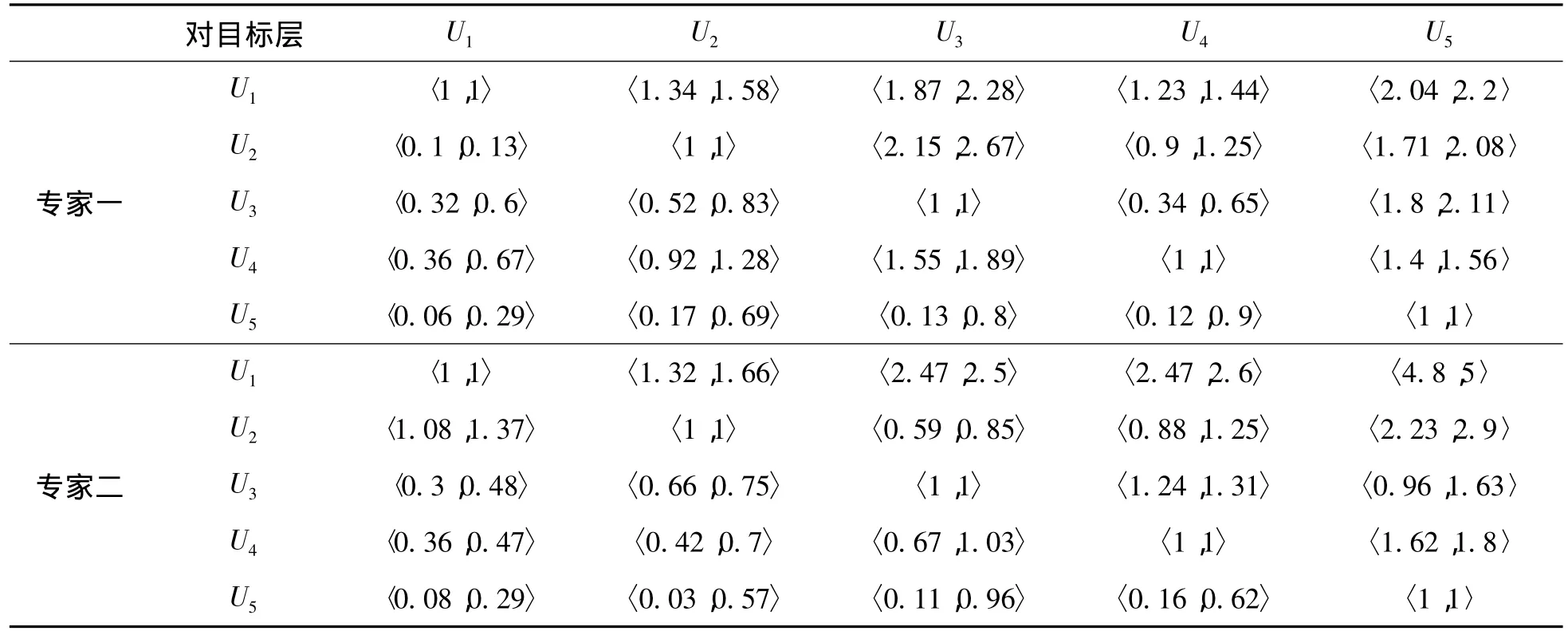
表2 準則層各屬性對目標層的重要度及權重排序

對于表2，由公式(1)可以得到相應的可拓區間判斷矩陣，即:

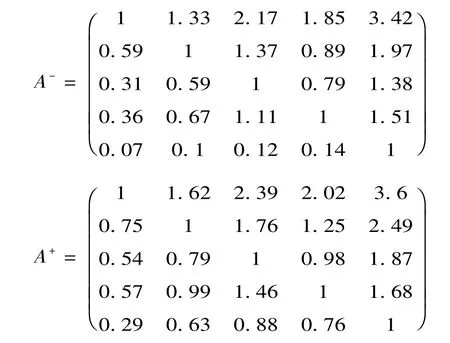
求得A－，A+的最大特征值所對應的特征向量x－=(0.753，0.457，0.306，0.355，0.065)T，x+=(0.686，0.468，0.336，0.377，0.234)T。

由公式(2)得:k=0.939，m=1.198，滿足 k＜1＜m，故判斷矩陣的一致性較好。

由式(3)得:權重量 S1=〈0.707，0.822〉，S2=〈0.43，0.561〉，S3=〈0.287，0.402〉，S4=〈0.334，0.452〉，S5=〈0.061，0.280〉。

由式(4)得:P1=V(S1≥S5)=4.556，P2=V(S2≥S5)=2.855，P3=V(S3≥S5)=2.044，

P4=V(S4≥S5)=2.32。通 過歸一 化得到 準則層各指標對目標層的單排序 P=(0.357，0.224，0.160，0.182，0.078)，同理可逐級計算其他指標結果，見表3。

(二)確定評價因素集合

根據表1的訂單融資模式下供應鏈金融風險評價指標，則U={借款企業訂單完成能力，下游核心廠商資信狀況，物流企業監管能力，供應鏈運營狀況，環境風險};U1={原材料采購效率和質量，產品生產能力，產品運輸能力，售后服務能力，貸款回收能力};U2={行業地位，信用等級，盈利能力，償債能力};U3={自律能力;監管水平};U4={合作密切程度，以往履約情況，信息化程度};U5={宏觀環境，行業環境}。

(三)確定評價評語集合

評價評語集為V={風險很小，風險小，風險一般，風險大，風險很大}，并設相應的分值為V={100，80，60，30，0}。

(四)確定隸屬度矩陣

建立隸屬度函數是為了將不同量綱的評價指標綜合成一個總的隸屬度。下面采用專家打分法，由兩個專家組共30人對各級指標的各項指標進行打分，得到一個評價矩陣，然后歸一化處理，即可得到單因素評價矩陣。

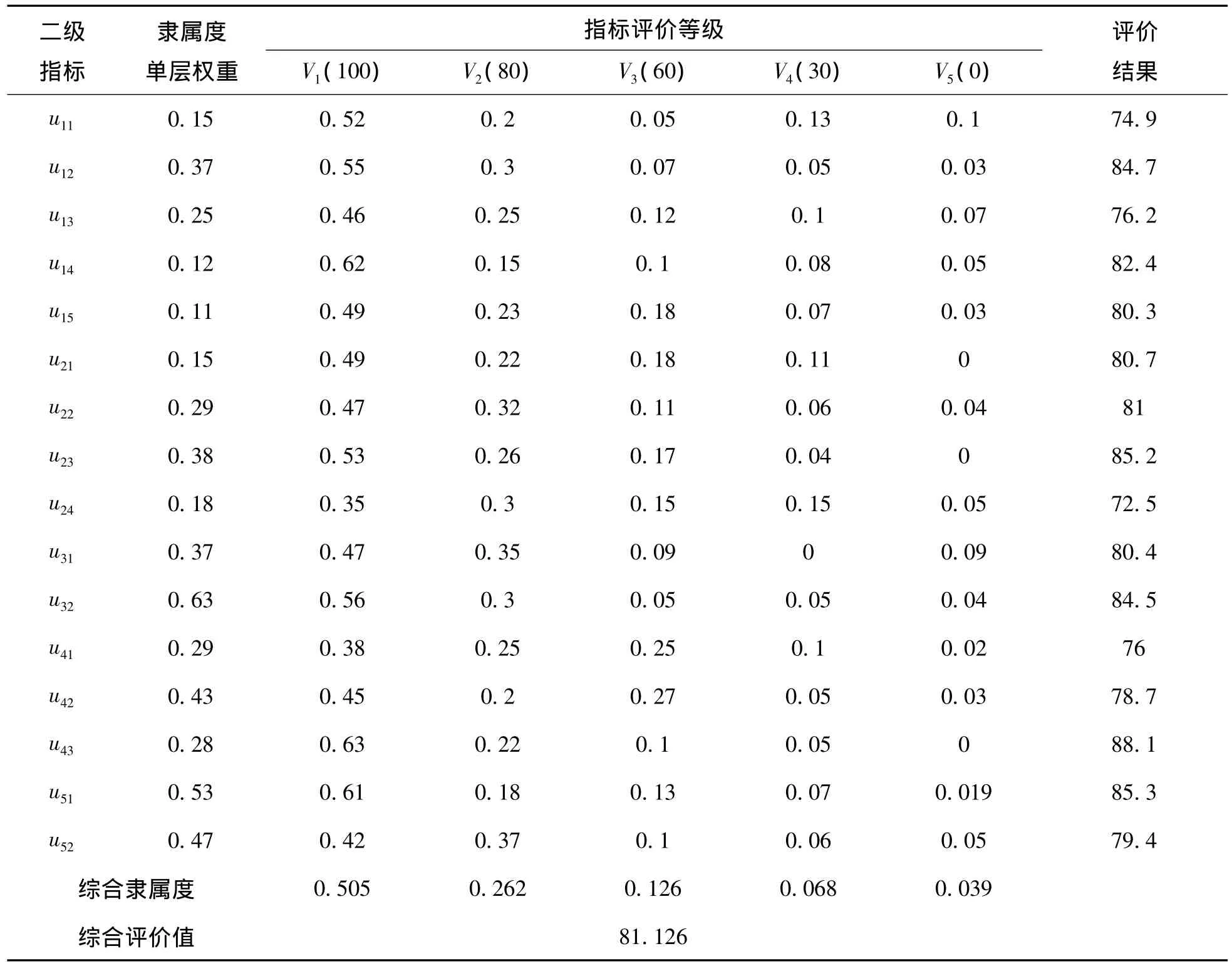
表3 訂單融資模式下供應鏈金融風險綜合評價結果

由式(9)得 B=(0.505，0.262，0.126，0.068，0.039)T，再由式(10)得到訂單融資風險綜合評價值G=81.126，說明該企業此筆訂單融資業務風險較小。

五、結論

構建了訂單融資風險評價指標體系，提出了采用可拓層次分析與模糊綜合評價相結合進行訂單融資風險評價的方法。該方法避免了傳統層次分析法的試算過程，克服了傳統層次分析法在專家經驗判斷的模糊性及判斷矩陣一致性方面的不足。實例表明，該方法合理、方便，對供應鏈金融服務中訂單融資業務的風險評價有一定借鑒意義。

［1］鄧愛民.基于BP神經網絡的訂單融資風險預警模型［J］.情報雜志，2010(11):23 －28.

［2］霍艷芳.供應鏈金融創新下分次贖貨模式分析［J］.物流科技，2011(7):96－99.

［3］李澤平.中小企業動產質押融資風險與控制策略分析［J］.財會通訊，2011(23):144 －145.

［4］汪守國.供應鏈融資模型及其風險分析［J］.商業時代，2009(22):75－76.

［5］周敏.基于模糊可拓層次分析法的物流客戶滿意度研究［J］.物流技術，2011(4):78－81.

［6］李毅學.物流金融創新下的訂單融資業務風險分析與管理［J］.當代財經，2008(12):66－70.

［7］Saaty T L.The analytic hierarchy process［M］.New York:Mc Graw-Hill，1980.

［8］高潔.可拓層次分析法研究［J］.系統工程，2002(5):6－11.

［9］王桂萍.基于模糊可拓層次分析法的數控機床綠色度評價方法及應用［J］.機械工程學報，2010(3):141－147.

［10］ZHANG Jing.New LCA approach with fuzzy evaluation［J］.Journal of Beijing Institute of Technology，2001(1):56－62.