基于PAADCP的海流流速的誤差分析及校正方法

鄭 一, 岳 軍, 紀乃華, 施國全, 韋俊霞

(1. 青島理工大學 理學院 數值計算與應用研究所, 山東 青島 266033; 2. 杭州中船重工第七一五聲學研究所, 浙江 杭州 310012)

與陸地測量相比, 由于海水的實時動態活動, 使得同一觀測量無法進行重復觀測; 又由于具有比陸地測量更多的噪聲干擾源, 導致海洋測量缺乏必要的效果質量檢查與核準手段[1-2]。如何界定海流流速的誤差大小, 特別是確認海流流速的誤差參考真值或基準值問題以及誤差校正方法, 是海試測量中一個基本的重大問題。本文分析相控陣聲學多普勒海流剖面儀(phased array acoustic Doppler current profiler, PAADCP[3-4])對海洋流速進行檢測的原理和方法[5-6], 利用PAADCP海試檢測數據, 給出粗差校正的動態反饋控制濾波算法, 基于小波多尺度分析方法[7-8]對海洋流速降噪處理, 分析影響海流流速的誤差來源, 估計誤差精度, 建立了海流流速的誤差分析與校正方法。

1 PAADCP的測速原理

PAADCP的基本原理是利用水聲換能器向海水介質發射特定頻率的定向聲脈沖信號(取4個不同的方向), 并接收從海水中聲波散射體上反射的回波信號。其主要過程是: 首先, 利用PAADCP發射的前后左右4個波束分別解算出4個速度v1,v2,v3,v4; 然后, 根據標定1＃波束與電羅經艏向的安裝誤差角α, 通過電羅經測得的航向角heading, 得到 4個方向的海水參考層相對運動速度; 最后, 再根據電羅經和GPS數據, 計算絕對速度[6,9-10]。

2 海試測流數據的誤差分析及校正方法

在測量學研究領域, 人們按照誤差的大小、特性及產生誤差的原因將其劃分為粗差、系統誤差和隨機誤差三大類型。粗差是指在數據獲取、數據傳送和數據加工過程中, 由于不規則的差錯而造成的, 通常指那些比正常值大得多或小得多的異常數據。系統誤差是指由于某種物理的、機械的、技術的、儀器的或作業人員的原因造成的, 具有一定的規律性, 頻率較低。隨機誤差是指由觀測條件(使用的儀器、外界環境和觀測者)引起的噪聲干擾。隨機誤差與系統誤差的區別主要體現在: 它的大小和正負符號都沒有規律性, 且頻率高[11-13]。

2.1 海試數據的粗差判定及其校正

粗差問題是海洋測量資料質量檢查和質量控制中的一個非常重要的、必須先期校正的問題。PAADCP數據粗差校正的效果如何, 直接影響到下一步的系統誤差和隨機誤差的校正效果, 直接影響海洋內波判斷條件是否奏效, 進而影響內波識別與特征信息提取等關鍵技術指標[14]。針對海洋內波現場測量技術及工程數據處理的需要, 我們建立了粗差動態反饋校正算法。

粗差動態反饋校正算法的物理原理是: 在監測儀器正常平穩工作狀態下, 海洋觀測量應是連續的、慢變的、平滑變化的。也就是說, 下一時刻的真實數據, 受到前期所得采樣數據的直接影響; 相鄰采樣數據之間的變化差異過大, 說明出現粗差, 應該校正; 利用預測數據和原來數據的變化率再進行下一時刻的預測, 對粗差校正后的數據再一次動態平滑校正, 以減少系統誤差和隨機誤差。

因此, 我們提出粗差處理的基本原則是: 由于海試的各個觀測量是連續的、慢變的、平穩變化的, 我們用觀測量的變換率大于某一閾值來區分粗差; 粗差可以用某一鄰域的數據取其平均來校正。

以船航向角heading的數據處理為例, 粗差動態反饋校正算法是:

第一步: 初值賦值: heading(k);

第二步: 判斷粗差: 相鄰的數值滿足變化率

heading(i)- heading(i-1) ＞ 25;

第三步: 粗差校正:

若heading(i)是粗差, 令

heading(i) = (heading(i-1)+heading(i-2)+ heading(i-3)+heading(i-4))/4;

若heading(i)不是粗差, 令heading(i)=heading(i);

第四步: 循環處理: 返回到第二步;

第五步: 動態平滑: 對heading(k)進行9點動態平均處理。

根據PAADCP的海試實測數據, 利用我們的粗差動態反饋校正算法, 航向角heading的粗差校正及其效果對比見圖1。可見, 我們的粗差校正效果是合理的, 精良的。

圖1 航向角粗差及粗差校正 Fig. 1 Heading angle gross error and heading angle gross error correction

2.2 海試測流數據的系統誤差、隨機誤差及其校正

在海流流速測量中, 導致流速誤差的主要誤差源有: 海況潮位影響、海流剖面儀四波束角偏位、聲速變化或器差改正誤差、船舶姿態(含橫搖角、縱搖角、升沉及首尾搖動)、測試中心定位與測速延時、船速對海流影響、數據后處理等。海洋測量, 從監測前的儀器校準到海上的觀測作業, 再到測量結束后的數據處理各個環節, 都不可避免地受到各種誤差源的干擾和影響[11-13]。這些誤差源的干擾和影響, 或產生粗差, 或導致低頻的、有統計規律的系統誤差, 或產生高頻的、無規律可循的隨機誤差。

為分析方便, 我們將內波流場流速構成矩陣形式

其中xij表示第i層、第j個時刻采樣點的內波實測流速數據。

在交叉點P(i,j)處, 經過觀測值的粗差處理后, 可建立如下形式的誤差方程式

我們按照上述校正原則, 利用MATLAB工具軟件, 利用2007年7月19日海試測流數據的第4層(即深度為106 m, 位于內波中間層)的數據進行多尺度小波分解[15-16]。取一維小波函數db6, 作6層分解, 分別得到6個近似系數A1～A6和細節系數D1～D6, 具體分解圖形見圖2。實際上,高頻的細節系數D1～D3包含了隨機誤差成分, 低頻的近似系數A1～A3包含了系統誤差成分, 近似系數A4就是我們選定的校正值或真值[14]。

圖2 實測垂向流速數據的6尺度小波db6分解 Fig. 2 The decomposition of 6 scaling wavelet with db6 for vertical velocity data

3 海試測速數據的誤差分析與應用

3.1 數據精確度

長期以來, 在國內主要應用最大絕對誤差的概念。對溫鹽深儀器的精度指標進行評價, 通常取儀器所測的全部數據中與真值相比偏差最大的測量值定為該儀器的精度指標。

聯合國教科文組織 (UNESCO)關于海洋科學的第54號文件在笫五章中提出: 數據處理中規定精確度(Accuracy)采用均方根 (root-mean-squre deviation)誤差。據了解, 不少國家都采用均方根誤差分析方 法[17-18], 一致認為這種處理方法在海洋測量中是比較合理的[19-20]。

3.2 海流流速的誤差界定

按照上述海洋數據處理的精確度含義, 海流流速的精確度指標定義為均方根誤差。

然而, 由于海洋試驗的不可重復性和海洋環境的特殊性, 海洋測量數據的參考真值或基準值如何選定呢？或者說, 什么樣的數據才可以認為它接近了真值？即, 海流流速的均方根誤差(誤差限)到底多大, 才能是工程上可以接受、認可的呢？

在一般海水運動問題中, 對中、高緯度的大、中尺度問題, 在傳統近似中忽略垂向流速, 認為垂向流速接近于零。內孤立波引起的最大垂向流速可達到0.2～0.3 m/s[1]。

在正常海況下測得的垂向流速也非常小。我們取2007年7月19日18:32:56至19:52:56期間80 min的海試垂向流速為例。在這段時間內, 沒有出現異常的海況變化。可以認為, 海洋試驗是在正常的情況下進行, 原始數據和降噪后的數據的波動也驗證了這一點。見圖3。

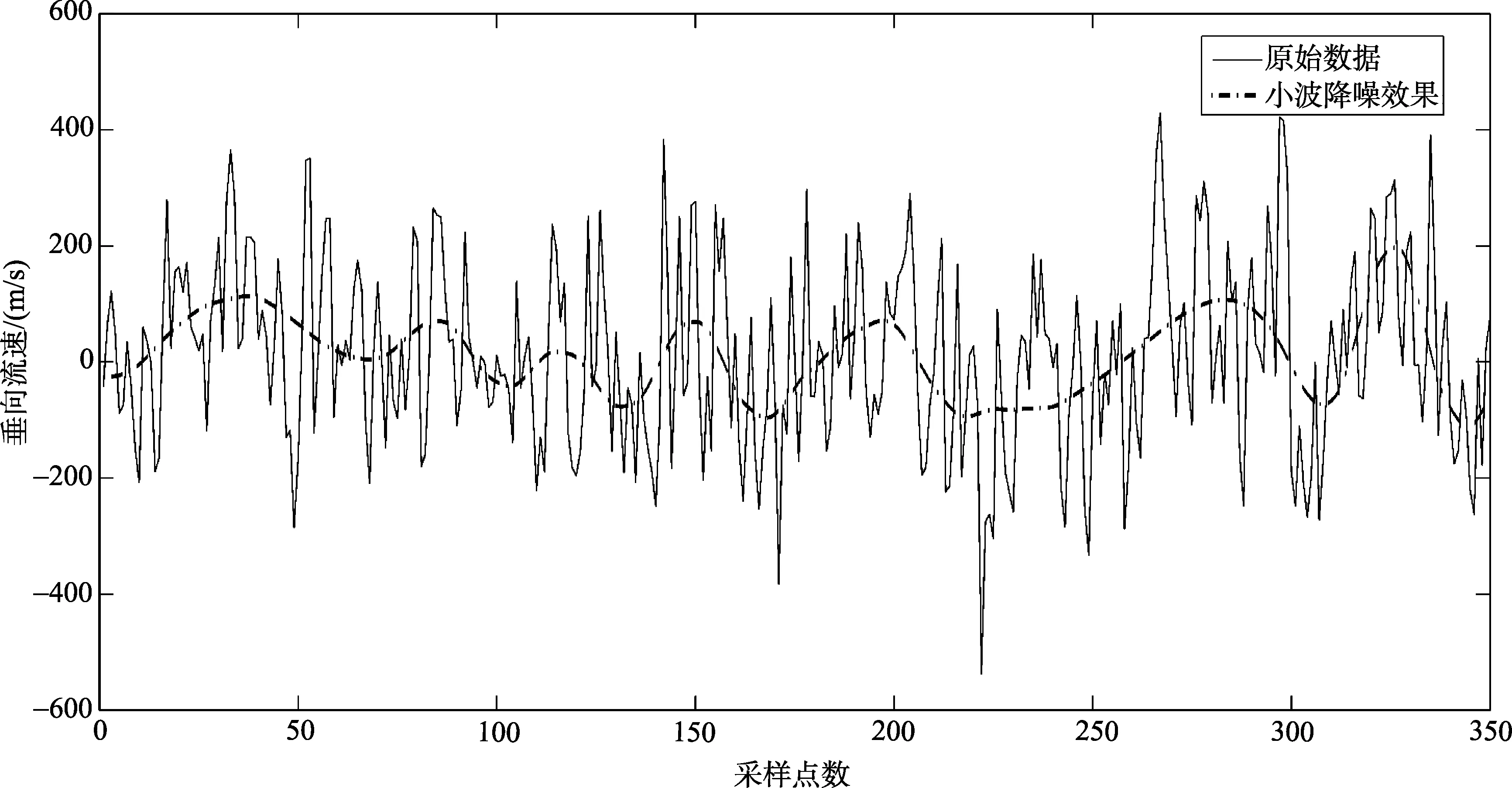
圖3 垂向流速波動及小波降噪效果 Fig. 3 Vertical velocity data and the data filtered by wavelet

我們分析誤差方程(2), 兩端取數學期望, 得到

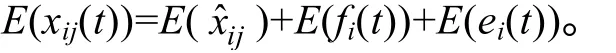
因為ei(t)是第i層t時刻的隨機誤差, 所以, 滿足關系式E(ei(t))=0。又因為是垂向流速的校正值或真值, 在正常海況條件下也有E()=0。因此, 得到均值關系式

由于fi(t)是系統誤差, 本身具有統計規律性, 均值關系式(3)說明: (1)各層流速的數學期望E(xij(t))不能出現大的波動。否則, 說明系統誤差變化較大, 應檢查系統誤差源。(2)各層流速的數學期望E(xij(t))應該接近于零。否則, 說明系統誤差影響較大, 應檢查和校正系統誤差。上述兩條性質, 可以作為海試測速誤差分析的一個基準標準。即, 測量海流垂向流速的各層均值接近于零, 并且沒有大的波動。

海洋測速成果的總體測速誤差精度采用均方差

來評定檢測海流流速成果的誤差精確度。

根據上述分析, 我們利用2007年7月19日海試實測數據, 去除海面下42 m盲區[6,14], 得到各層海流垂向流速均值和標準差如圖4所示。

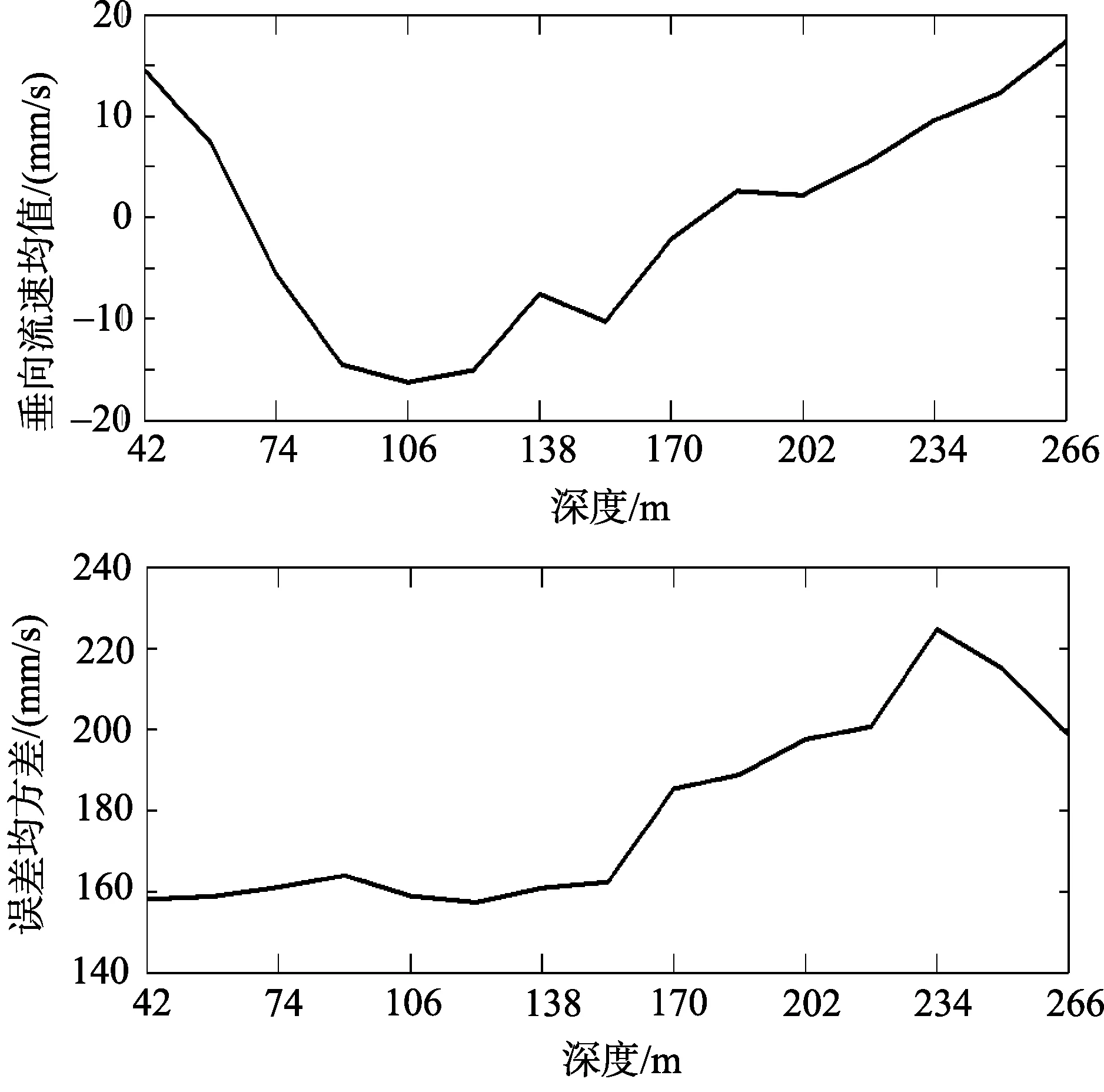
圖4 垂向流速均值與誤差均方差 Fig. 4 The mean vertical velocity and mean square error

可見, 測速成果的垂向流速慢變平穩, 均值大小為±0.02 m/s, 測速誤差精確度小于0.23 m/s。

3.3 海流流速的后處理效果

我們將上述誤差分析方法和降噪算法運用到海試數據后處理中。

圖5是采用海試實際監測數據, 利用粗差動態反饋校正算法和小波降噪校正算法, 通過等流速線和顏色棒表示的內波水平流速檢測圖[14]。可見內孤立波結構非常清晰, 并且數據波動也偏小, 更加符合海況變化的慢變、平穩狀態。

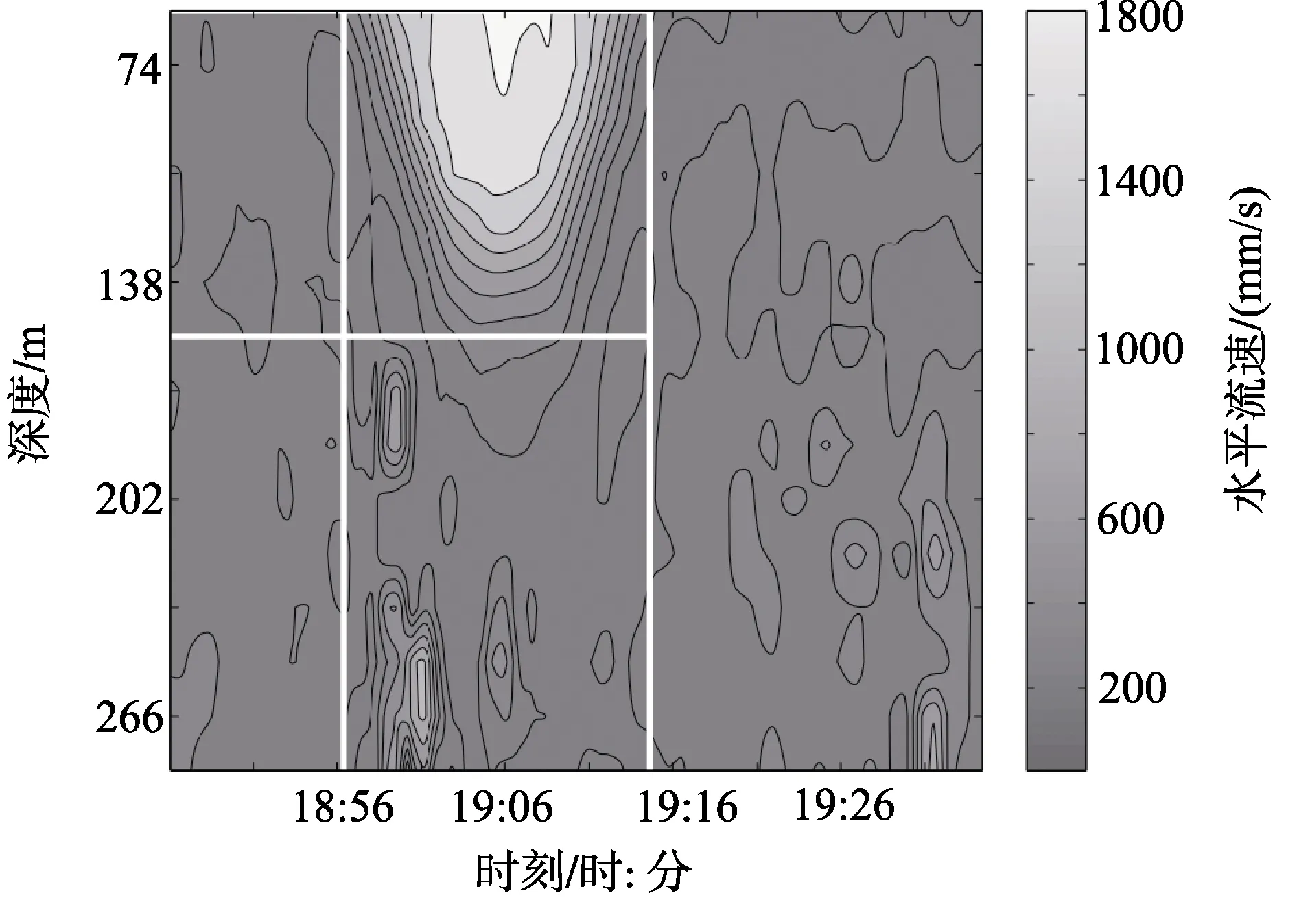
圖5 算法校正效果檢測圖 Fig. 5 The effect figure by correction algorithms

4 結論

本文通過對海流流速測量誤差的定性、定量分析及計算機數值模擬, 認為: 首先必須進行測流數據的粗差區別與校正, 然后再進行系統誤差和隨機誤差的處理, 利用粗差動態反饋濾波并結合多尺度小波分析是一個好方法。利用同層的垂向流速應位于同一水平線上的物理意義, 提出了利用垂向流速是否位于同一水平線作為誤差分析的基準值, 得到成果的誤差精確度小于0.23 m/s。所用方法對于進一步應用到海洋內波的聲學監測和內波特征的研究具有重要的意義。

[1] 方欣華, 杜濤. 海洋內波基礎和中國海內波[M]. 青島: 中國海洋大學出版社, 2005: 12-15, 308-308.

[2] 顏梅, 范植松, 傅深波, 等. 海洋內波預報技術研究的必要性與可行性初探[J]. 海洋預報, 2010, 27(2): 76-81.

[3] 沈斌堅, 張國棟. 相控陣聲學海流剖面儀性能指標考核方法探討[J]. 聲學與電子工程, 2004, 3: 31-33.

[4] 李震, 馮雷, 邱薇,等. 幾種測流設備的比測試驗及分析[J]. 海洋技術, 2006, 25(4): 42-45,64.

[5] Pan Xi, Cui Zhanzhong. Doppler signal simulation and analytic system for radio fuze[J]. Journal of Beijing Institute of Technology, 2008, 17(1): 62-66.

[6] 孫文俊, 沈斌堅. 海洋內波ADCP監測技術研究[J]. 熱帶海洋學報, 2010, 29(4): 170-173.

[7] 高成, 董長虹, 郭磊, 等. Matlab小波分析與應用[M]. 北京: 國防工業出版社, 2007: 10-12,104-122.

[8] Xing Qi, Roseanna M. Neupauer wavelet analysis of characteristic length scales and orientation of two-dimensional heterogeneous porous Media[J]. Advances in Water Resources, 2010, 33(4): 514-524.

[9] 黃謨濤, 程國君, 歐陽永忠, 等. 海洋測量誤差處理技術研究進展與展望[C]//中國測繪學會. 中國測繪學會第十五屆海洋測繪綜合性學術研討會論文集. 北京: 中國測繪學會, 2003: 6.

[10] 黃雄飛, 周徐昌, 何建軍. 聲學多普勒海流剖面儀誤差源分析[J]. 聲學與電子工程, 2006, 4: 1-3.

[11] 張雪, 胡曉琴. 陣列信號處理中的誤差分析概論[J]. 科技信息, 2011, 35: 171-171.

[12] 沈斌堅, 唐義政, 胡益群, 等. 國產寬帶相控陣聲學多普勒海流剖面儀[J]. 聲學與電子工程, 2005, 1: 1-3.

[13] Blair H B, Ramon G C, Kent L D．Performance of a broad-band acoustic Doppler cerrent profiler[J]．Journal of Oceanic Engineering,1991,16(4): 402-407．

[14] Zheng Yi, Yue Jun, Sun Xiaofeng, et al. Studies of filtering effect on internal solitary wave flow field data in the South China Sea using EMD[J]. Advances in Environmental Science and Engineering, 2012, 523: 1422-1425.

[15] 劉孟德, 杜麗斌, 任國興. 數字濾波及小波分析技術在海流測量中的應用[J]. 山東科學, 2011, 24(6):71-74.

[16] Quellec G. Adaptive nonseparable wavelet transform via lifting and its application to content-based image retrieval[J]. IEEE Transactions on Image Processing, 2010, 19(1): 25-35.

[17] Petra N, De Caro D., Garofalo V, et al. Truncated binary multipliers with variable correction and minimum mean square error[J]. IEEE Transactions on Circuits and Systems, 2010, 57(6): 1312-1325.

[18] 朱華, 葛世榮. 結構函數與均方根分形表征效果的比較[J]. 中國礦業大學學報, 2004, 33(4): 396-399.

[19] 劉雪堂, 林紅軍. CTD剖面儀現場定標和誤差分析[J]. 海洋技術, 1990, 9(1): 18-24.

[20] GBl2327.1998, 海道測量規范[S].