可變單縫衍射微小尺度測量系統研究

呂洪方，譚小平，吳鐵山

（江漢大學 物理與信息工程學院，湖北 武漢 430056）

0 引言

在大學物理實驗中，測量單縫衍射的光強分布是一個重要的光學基礎實驗［1］，在理論研究和實驗教學中占重要地位。通過該實驗可以直觀地驗證光具有波動性，還可以測量衍射光強的分布。在實驗中，需要學生手動改變光敏探頭的位置，測定各點的光強，然后在此基礎上進行數據分析和畫曲線圖。學生要在有限的課堂實驗時間里花費大量時間和精力去測量、計算、處理數據，因而理論分析和誤差分析的時間相對減少，影響其對理論的理解和掌握。目前，各高校越來越重視實驗創新性教學改革，因此，改進單縫衍射光強分布實驗儀器和推廣基于單縫衍射原理的各種應用顯得尤為重要。

近年來，越來越多的研究者關注單縫衍射自動測量系統，利用該系統來測量金屬絲的直徑、物質的膨脹系數以及產品的畸變等［2－7］。結合之前研制的邁克爾遜干涉微小尺度測量系統［8］，本文利用激光的單縫衍射原理，研制了一款微小尺度測量系統。該系統的綜合應用性強，可以培養和鍛煉學生的實驗、科研、綜合創新能力。

1 測量原理

圖1 單縫衍射原理圖

單縫衍射原理如圖1 所示，圖中的條紋寬度隨著單縫寬度的改變而改變。如果能將待測物體的微小尺度轉化為縫寬a 的變化，就可以對待測物體進行精密測量。實驗中對單縫進行改造，通過杠桿原理使之能將物體的微小尺度轉化為縫寬a 的改變（見圖2）。將待測物體放置在滑動載物臺上，根據待測物體尺度的不同，將滑動載物臺放置在合適的位置，然后用定位螺桿固定。也就是選擇一個比較合適的杠桿力臂比，使屏上的衍射條紋清晰明亮。放入待測物體后，縫寬會相應地變小，屏上的衍射條紋間距就相應地變大。測量放置待測物體前后條紋間距的變化和杠桿力臂比，就可以得到待測物體的尺度。

圖2 杠桿示意圖

根據楊氏單縫衍射理論，第k 級暗條紋位置為

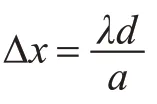
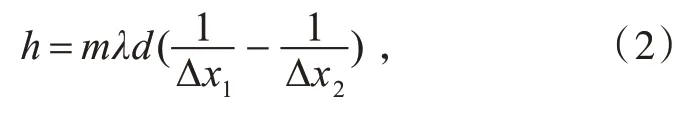
其中Δx1、Δx2分別為放入待測物體前后相鄰的兩條暗條紋的寬度。

2 系統構成

可變單縫衍射微小尺度測量系統設計結構框圖如圖3 所示。測量過程總體上分為4 個部分：①將待測物體放置在定位螺桿下固定，根據待測物體尺度的大小，通過滑動載物臺放置在杠桿的不同位置，實現將待測物體的尺度通過杠桿轉化為單縫寬度的改變；②采用635 nm、50 mW 的半導體激光器照射狹縫；③光電轉化部分，由一可控轉速的直流電機帶動光電池進行掃描，得到衍射區域內條紋明暗程度的光電轉化信號強度；④信號放大、模數轉換、數據采集、數據傳輸以及數據處理部分，將光電池的信號先進行放大，然后通過采集卡進行數模轉換與采集，通過網線RJ45 接口傳輸給計算機進行處理與結果顯示。

圖3 可變單縫衍射微小尺度測量系統設計結構框圖

可變單縫衍射微小尺度測量系統實物如圖4所示。

圖4 可變單縫衍射微小尺度測量系統

3 測量結果與分析

該測量系統可對剛性的微小物體進行測量，比如頭發絲、細導線、薄片等。為檢驗該系統的測量精度，選用標準塞尺進行測量。測量結果及分析見表1。

表1 3 種不同尺度塞尺的測量結果

表1 中算術平均值標準偏差計算公式為

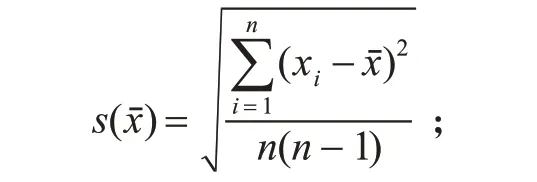
不確定度計算公式為

測量結果的標準偏差較小，不確定度很小，說明測量結果可重復性高、可信度高。誤差主要來源于光源的穩定度、系統的震動和直流電機工作的穩定度。

4 結語

可變單縫衍射微小尺度測量系統是繼邁克爾遜干涉微小尺度測量系統之后又一款基于不同的實驗原理、實現同一個目的的系統。這兩套系統的檢測部分基本相同，設計思路有相通之處。可變單縫衍射微小尺度測量系統同樣也具有可靠性好、操作簡便、工作穩定等優點。原理簡單，能清楚直觀地觀察到衍射條紋隨縫寬的變化情況，驗證光的波動性。同樣，該測量系統還具有比較好的擴展性，可以用來測量激光的波長，增強學生的動手能力，提高學生對實驗的興趣。該系統的研制與應用有助于學生科學系統地將不同學科的知識和技能有機地結合起來，直接運用于實踐，實現對學生進行綜合能力的訓練和培養，達到綜合創新的教學目的。

［1］ 周殿清. 大學物理實驗［M］. 武漢：武漢大學出版社，2002：278－281.

［2］ 戴玉梅，劉彬. 激光單縫衍射實驗拓展應用的研究［J］.沈陽大學學報，2010，22（2）：32－34.

［3］ 潘華錦，張麗，馬春庭.利用CCD 測量單縫衍射的光強分布［J］.計量與測試技術，2009，36（3）：57－58.

［4］ 陳磊，張凱，朱路揚. 單縫衍射自動測量系統的研究［J］.大學物理，2006，25（7）：28－32.

［5］ 邱淑榮. 對激光單縫衍射光強分布測量實驗的改進［J］.物理實驗，2001，21（11）：32－33.

［6］ 顧永建. 激光單縫衍射實驗中縫寬的精確測算［J］.大學物理實驗，2000，13（4）：27－29.

［7］ 鄭光平，李銳鋒. 單縫衍射測量金屬膨脹系數［J］. 物理實驗，2008，28（9）：36－37.

［8］ 呂洪方，譚小平.邁克爾遜干涉微小尺度測量系統的研究［J］. 江漢大學學報：自然科學版，2012，40（1）：41－43.