基于高頻數據滬深300股指期貨量價關系研究＊

張小勇，任德平，2

（1.湖南大學 工商管理學院，湖南 長沙 410072； 2.長沙理工大學 經濟與管理學院，湖南 長沙 410114）

一 引 言

由于量價關系是股票技術分析理論的重要基石，也是廣大投資者在投資實踐中判斷市場或個股運行趨勢的主要手段之一，因此，量價關系研究一直以來是金融學領域的研究熱點之一。

早在1970年，Crouch［1］發現無論指數還是個股，其絕對價格收益與交易量呈現同期正相關關系。Karpoff［2］研究發現成交量與股票絕對收益率變化呈現一種正相關關系。Gallant等［3］進一步證實了該結論。國內的陳怡玲和宋逢明［4］對中國股市實證發現日交易量與日絕對價格變化之間也存在線性正相關關系。后來有很多學者試圖從各個角度對這一正向相關關系加以解釋，但始終沒有得出一個統一的結論。Clark［5］提出了混合分布假說，認為市場一種潛在不可觀察的信息流是導致交易量和價格波動變化的共同驅動因素。Copeland［6］提出了連續信息到達假說，認為市場信息逐步向外擴散導致了價格波動和交易量同步擴大。Harris和Raviv［7］構建了“判斷差異模型”，認為投資者對市場同一信息的判斷偏差導致了交易的發生，股價絕對變化與成交量表現出正相關關系。Wang［8］建立了“理性預期資產定價模型”，認為投資者之間擁有的私人信息和投資機會不對稱導致了成交量與價格變化的正相關。

盡管如此，上述研究主要集中價格變化與成交量的同期相關上，對量價關系背后的驅動因素沒做深入探討。為了更深入地研究交易量與價格波動之間的關系，許多學者從更微觀的角度去探究量價關系背后的主要驅動因子。Kyle［9］研究了知情交易者的訂單流非平衡（order imbalance）對價格波動的影響。Jone等［10］將交易量分解成成交次數和平均交易頭寸來考察不同交易量成分對股價波動的影響，結果發現成交次數解釋了大部分股價波動率。Huang 和Masulis［11］使用倫敦交易所的數據進一步證實了他們的結論。Chan 和Fong［12］證實了訂單流非平衡可以解釋一部分股票收益，而且過濾訂單流非平衡的成交次數對股價波動率影響很小，因此推斷訂單流非平衡可能是量價關系主要驅動因子。Easley等［13］研究發現知情交易者更傾向于大額訂單交易，因此，認為交易頭寸可能包含更多價格信息。為了避免隱藏信息在市場提前暴露，知情交易者往往傾向于將隱藏信息通過大額交易拆分成許多小額交易的渠道來在市場上逐步釋放。Chakravarty［14］進一步證實了隱藏交易假設的存在，認為訂單流非平衡、成交次數包含更為豐富的股票價格信息。Chan和Fong［15］用高頻已實現波動率代替絕對價格收益來研究量價關系背后的驅動因子，結果發現成交次數能夠對量價關系形成有力解釋，交易頭寸和訂單流非平衡對量價關系的解釋力有限。Giot等［16］實證了連續樣本路徑方差和跳躍方差分別與交易量、交易頭寸、成交次數和訂單流非平衡之間的相關關系。Chevallier和Sevi［17］使用能源期貨市場日內高頻數據考察了已實現波動率及其衍生波動率與交易量、成交次數和交易頭寸之間的相關關系。

國內對量價關系的研究主要集中在相關性檢驗和因果分析上，張維、閆冀楠［18］采用Granger因果檢驗實證了上證指數，結果發現周收益對交易量具有明顯的線性因果關系，但交易量對收益率不具有線性因果關系。隨后，陳良東［19］利用因果檢驗和回歸分析對上證股市進行實證研究，結果顯示交易量與價格絕對變化存在顯著的正相關關系。王承煒等［20］實證發現滬深兩市都存在價格收益對交易量的的線性因果關系和雙向非線性因果關系。王杉、宋逢明［21］建立了簡單的量價關系模型進行實證，發現非知情交易者持倉量的變化和預期變化對量價關系有重要影響。梁麗珍［22］利用分量回歸法來分析中國股市的量價關系，結果發現中國股市具有“價量齊揚”和“價跌量縮”的現象。隨著金融高頻數據應用的逐步推廣，有的學者開始嘗試利用高頻數據來對量價關系進行研究。李夢玄、周義［23］使用滬深兩市高頻5 分鐘指數數據對量價關系進行了實證研究，結果表明兩市量價之間僅存在雙向線性引導關系，并不存在非線性Granger因果關系。郭梁、周煒星［24］通過高頻數據研究了中國股市個股的成交量與價格變化之間的關系，實證研究發現中國股市成交價格波動與成交量之間具有相關關系，量價關系曲線為一非線性凸函數。

綜合以上研究分析，國內學者主要集中在對中國股市交易量與價格波動之間正相關關系的檢驗和因果分析上，且多數停留在宏觀層面上的簡略分析，對量價關系背后的驅動因子的探索研究幾乎沒有，此外，鮮有學者對股指期貨市場的量價關系做出研究。因此，本文在MDH 理論的基礎上，以滬深300股指期貨為研究對象，通過建立相應的線性模型并結合滬深300股指期貨的高頻數據進行實證分析，以求能夠綜合全面地揭示我國期指市場量價之間的規律性特征。

二 研究方法介紹

（一）量價關系模型的建立

本文將通過建立簡單的線性模型來考察滬深300股指期貨的量價關系的變化，即以波動率作為被解釋變量和以交易量和其他影響因子作為解釋變量構建多元線性回歸模型來進行研究。為了綜合考察滬深300股指期貨的量價關系，本文將從基本量價關系、連續和跳躍波動的量價關系以及量價關系非對稱性等三方面來建立相應的線性模型進行研究。

（1）量價關系基礎模型

Chan 和Fong［15］研究發現已實現波動率代替絕對收益作為波動率的精確估計量可以更好地刻畫交易量與價格波動之間的關系。因此，本文將選取已實現波動率作為滬深300股指期貨價格波動率的有效估計量。由于我國股指期貨合約交割日為合約到期月的第三個星期五，其價格波動往往隨著期指臨近到期而變得日趨劇烈，同時也為了考慮周末效應對期指波動的影響，引進虛擬變量DUMMYt，Friday。另外，已實現波動率往往存在很強的自相關性，故在模型中將已實現波動率的滯后期考慮進來。基于以上分析，構建如下線性模型：

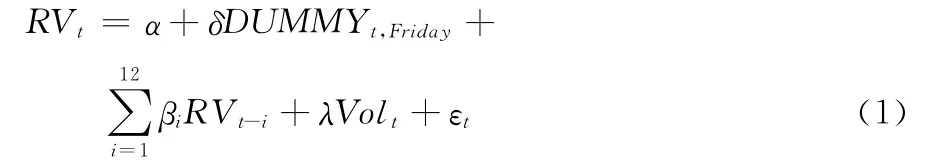
模型（1）是本文構建最基礎的量價關系模型，其中：RVt表示第t天所對應的已實現波動率，即：為第t天所對應的成交量。

為了進一步深入研究滬深300股指期貨之間的量價關系，以找出量價關系中最主要的驅動因素。我們根據Jones等［10］的研究將日成交量分解為日成交次數和平均交易頭寸，在模型（1）的基礎上都建了如下模型：

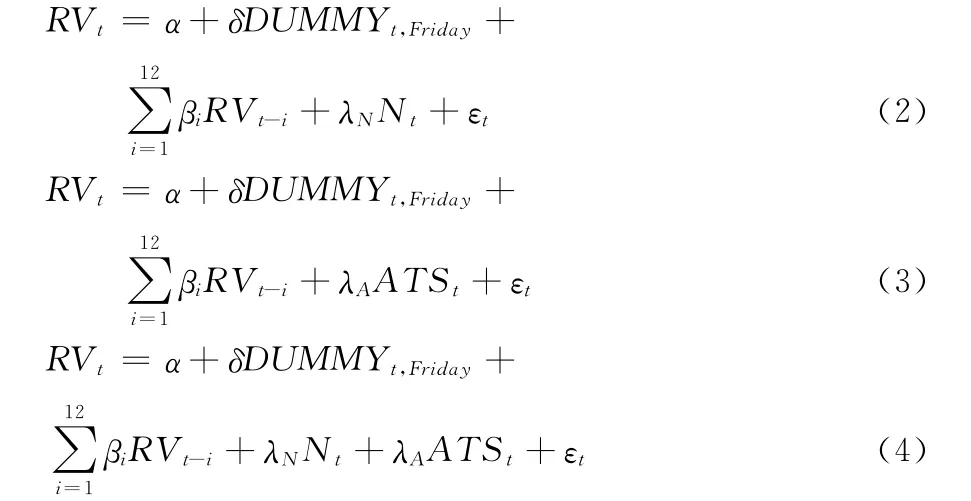
其中：Nt為第t天的成交次數，ATSt為第t天的平均交易頭寸（日成交總量除以成交次數），即

（2）連續和跳躍波動量價關系模型

Andersen和Bollerslev等［25］基于二次變差理論將已實現波動率分解成連續樣本路徑方差和跳躍方差。為了考察成交量對已實現波動率中連續樣本路徑方差和跳躍方差的影響，我們仿效Giot等［16］的建模原理，構建了如下模型：

（3）量價關系非對稱性模型

為了對資產價格下降時的風險進行準確度量，BNKS（2008）［26］針對已實現波動率提出了上偏已實現半方差（RS＋t）和下偏已實現半方差（RS－t）。Chevallier和Sevi［17］將它們應用到量價關系的非對稱研究上。為了檢驗滬深300股指期貨量價關系的非對稱性，我們參照Chevallier 和Sevi［17］的研究成果，建立了如下模型：

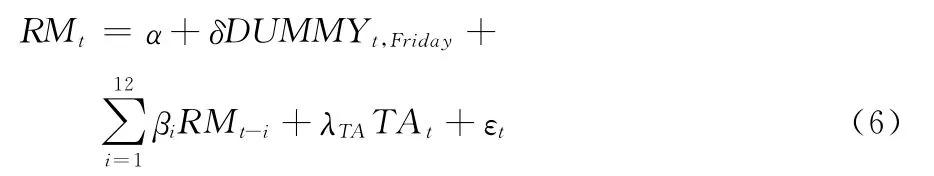
其中：RM＝｛RSt＋，RSt－｝，TA＝｛Volt，Nt，ATSt｝，RV＝RSt＋＋RS－，RSt＋、RSt－分別表示上偏已實現半方差和下偏已實現半方差，即：。對模型（6）的估計，我們仍將采用類似于模型（5）的估計原理，即：對RS＋t和RS－t分別按照（1）—（4）式進行估計，然后從總體上對滬深300股指期貨的量價關系的非對稱性進行準確判斷。

考慮到以上量價關系線性模型估計結果的殘差可能存在自相關或異方差性，為了提高模型的估計精度，本文除了跳躍波動以外都將采用OLS with Newey west估計法進行參數估計，對跳躍波動量價關系模型將仿效Giot等［16］采取TOBIT 回歸進行估計。然后，分別對各量價關系模型的估計結果進行細致分析，最后從總體上對滬深300股指期貨的量價關系進行歸納總結。

（二）跳躍方差的分離

由于上述量價關系的線性模型涉及到已實現波動率中跳躍方差，因此，我們有必要對已實現波動率中跳躍方差的分離原理做出簡單的說明。跳躍方差實際上為已實現波動率與跳躍穩健估計量之差，為了提高跳躍方差的分離有效性，我們還需要通過相應的統計量對顯著的跳躍波動進行檢驗。

首先，對于一個服從連續跳躍離散過程的資產對數價格，我們將其樣本期內t日離散時間區間的日內收益率定義為：rt，j＝pt，j－pt，j－1。根據Andersen和Bollerslev［27］對已實現波動率的定義，我們可知第t日的已實現波動率為RVt＝（M為日取樣次數）。

其次，Barndorff－Nielsen和Shephard［28］，［29］考慮市場存在有限次跳躍波動的情況下而提出了“已實現”雙冪次變差（Realized Bipower Variation，RBV），它可以作為已實現波動率中的跳躍成分的穩健估計量。

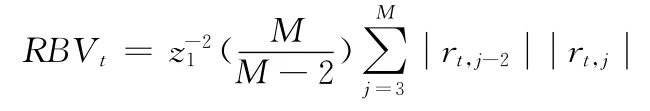
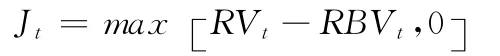
再次，為了提高跳躍波動的估計精度，我們采用Huang和Tauchen［30］提出一個漸近服從標準正態分布的Zt統計量來對顯著性跳躍性波動進行檢驗。即：

Andersen等［31］提出了一種全新的估計量MedRV 來代替RBV 作為估計跳躍波動的穩健估計量可以明顯提高檢驗顯著跳躍性方差的有效性。即：

相應的，Zt統計量中的RTQt將由MedRTQt來代替。即：

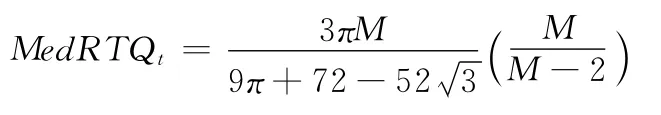
通過對Zt統計量的計算，在1－α的顯著性的水平下（α＝99%），我們得到離散跳躍方差的估計量：

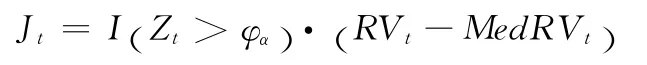
連續樣本路徑方差估計量：

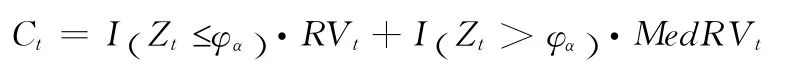
三 實證分析

（一）樣本數據獲取及基本分析

本文以滬深300股指期貨當月連續指數為實證樣本對象，選取樣本期2011年4月11日至2012年4月10日共計244個交易日的5分鐘高頻數據進行實證分析。由于滬深300股指期貨的交易時間為上午9：15－11：30，下午13：00－15：15，交易時長為4個半小時，比股市多出半個小時，因此，我們剔除交易時間外的數據還剩下13140個有效數據，平均每天約為54個數據。選取的樣本指標為交易時間、收盤價、成交量及成交次數，數據來源于同花順行情分析軟件。

表1記錄了滬深300股指期貨各實證統計量描述性統計特征的相關數據。通過分析，已實現半方差的均值（RS＋和RS－）為已實現波動率的一半，且上偏已實現半方差的均值要約大于下偏已實現半方差的均值，這說明滬深300股指期貨市場期指價格上漲的風險要高于價格下跌的風險，也間接反映市場的投資者的交易策略傾向于做多，對市場做空相對謹慎。另外，已實現波動率中的連續成分所占比約為72.8%，這說明了連續波動成分相對跳躍波動成分在已實現波動率中占據主導地位。除跳躍波動以外，各統計量在滯后12階仍具有很強的自相關性，因此，針對各量價關系模型中考慮滯后變量的相關性影響的建模分析具有一定的統計基礎。

表2給出了滬深300股指期貨各統計量之間的相關系數，我們發現已實現波動率與成交量表現出明顯的正相關關系，即期指波動隨著成交量的放大而不斷加劇，這與國內外量價關系正相關性的結論相一致。成交量（Vol）與平均交易頭寸（ATS）的很高的相關性強度，且它們之間的相關系數要明顯高于成交量（Vol）與成交次數（Num）的相關系數，這說明交易頭寸與成交量包含大量類似的市場信息成分，此外，已實現波動率（RV）與平均交易頭寸（ATS）也表現出很強的相關性，這與Chan和Fong［15］及Giot等［16］研究的結論截然相反。滬深300股指期貨的已實現半方差與平均交易頭寸（ATS）保持很強的正相關關系，有別于Chevallier和Sevi［17］在能源期貨上研究發現的負相關關系，且上偏已實現半方差（RS＋）與成交量（Vol）之間的相關系數要明顯高于下偏已實現半方差（RS－）與成交量（Vol）之間的相關系數，但都與成交量保持正向的相關關系。相比跳躍波動成分下微弱的量價相關性，連續波動成分與成交量之間擁有更強的相關關系。

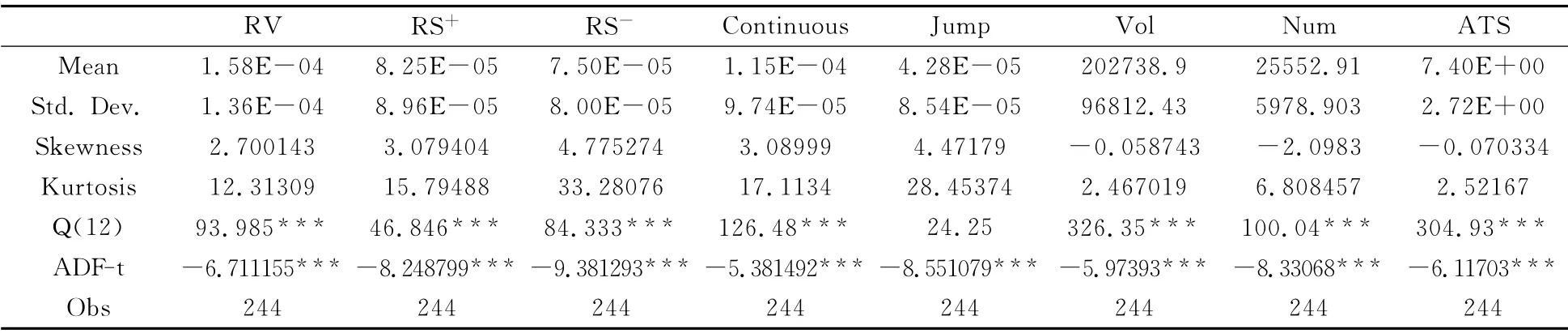
表1 滬深300股指期貨各指標描述性統計分析

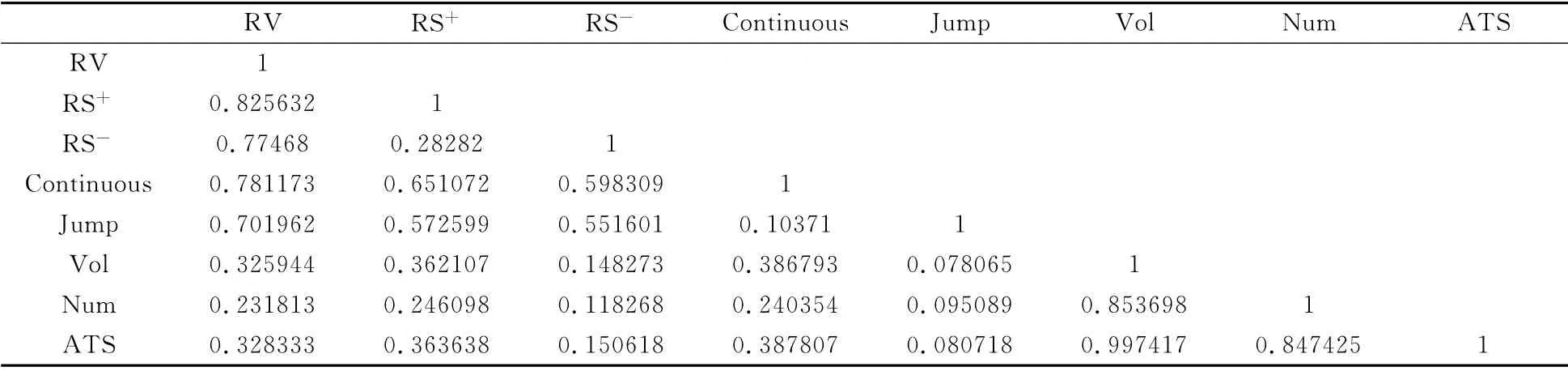
表2 滬深300股指期貨各統計量相關系數矩陣

（二）量價關系模型的估計及分析

在上述各統計量描述性特征及相關性分析的基礎上，我們對滬深300股指期貨的量價關系進行了初步論證。為了進一步探究我國滬深300股指期貨市場的量價關系內在表現形式，以便我們挖掘出隱藏在量價關系背后的驅動因子及相關動態特征，我們將分別對文中建立的量價關系基礎模型、連續和跳躍波動量價關系模型及量價關系非對稱模型進行實證參數估計，并結合實際市場情況加以分析。

關于未來，馬國新說：“我沒有什么豪言壯語，也不表什么決心，我只要扎扎實實的干好本職工作，無愧于黨和人民，這就足夠了。”

1.量價關系基礎模型估計

表3記錄了量價關系基礎模型主要變量的參數估計結果，我們發現反映“周末效應”影響效應Dum 所對應系數在1%的顯著性水平下都不顯著，這說明“周末效應”對滬深300股指期貨的量價關系沒有形成明顯的影響。從RV－model（1）來看，成交量對已實現波動率存在顯著的正向影響，這說明市場波動伴隨成交量的放大而加劇，伴隨成交量的萎縮而減弱，即滬深300股指期貨市場呈現“價量齊漲”和“價量齊跌”的現象。將成交量分解成成交次數和平均交易頭寸再進行估計，由RV－model（2）和RV－model（3）參數估計結果來看，成交次數和平均交易頭寸都對期指波動存在顯著的正向影響，另外，RV－model（3）的Adjusted R2要大于RV－model（2）的Adjusted R2，這說明滬深300股指期貨市場的平均交易頭寸相比成交次數更好地解釋了期指的波動。當成交次數和平均交易頭寸同時加入到模型中進行估計時，成交次數前的系數并不顯著，Adjusted R2并沒有太大提高，從而進一步證實了平均交易頭寸在解釋期指已實現波動率中扮演著最為重要的角色，是期指量價關系背后的主要驅動因子，這與Giot等［16］在美國股票市場發現量價關系背后的驅動因子是成交次數，而不是平均交易頭寸的結論截然相反。這反映了我國期指市場的投資者對市場信息傾向于使用大單交易來做出反應，因而平均交易頭寸包含了更多的真實市場信息；而發達國家金融市場投資者的交易行為更符合隱藏交易假說相關理論，即將大單交易拆分成許多小單交易來隱藏市場信息，因此成交次數是量價關系背后驅動因子。

表3 量價關系基本模型的參數估計結果

2.連續和跳躍波動量價關系模型估計

表4和表5分別記錄了連續和跳躍波動量價關系主要變量的參數估計情況。經分析我們發現，成交量、成交次數和平均交易頭寸對已實現波動率的連續和跳躍成分都有著不同程度的正向影響。基于連續波動構建的量價關系模型參數估計結果在1%的顯著性水平下都是顯著的，而基于跳躍波動構建的量價關系模型參數估計結果在10%的顯著性水平下才顯著，這說明相比跳躍波動，連續波動的量價關系較為精確地反映了滬深300股指期貨的量價關系，同時也間接反映出連續波動成分包含了更多的已實現波動率的信息成分，因此，我們可以利用連續波動相關歷史信息對期指的已實現波動率做出預測。表4中的C－model（1）中的Adjusted R2要高于表3中的RV－model（1）中的Adjusted R2，即剔除跳躍波動后的量價關系模型的擬合優度有了明顯改善，這反映了期指的量價關系還受到跳躍波動所帶來的噪音影響。另外，結合表4和表5中的模型（2）（3）（4）來分析，我們發現無論是從待估參數大小還是從模型的擬合優度都顯示了平均交易頭寸做為量價關系背后的關鍵驅動因子，能夠更好地解釋連續和跳躍的波動的相關變化。

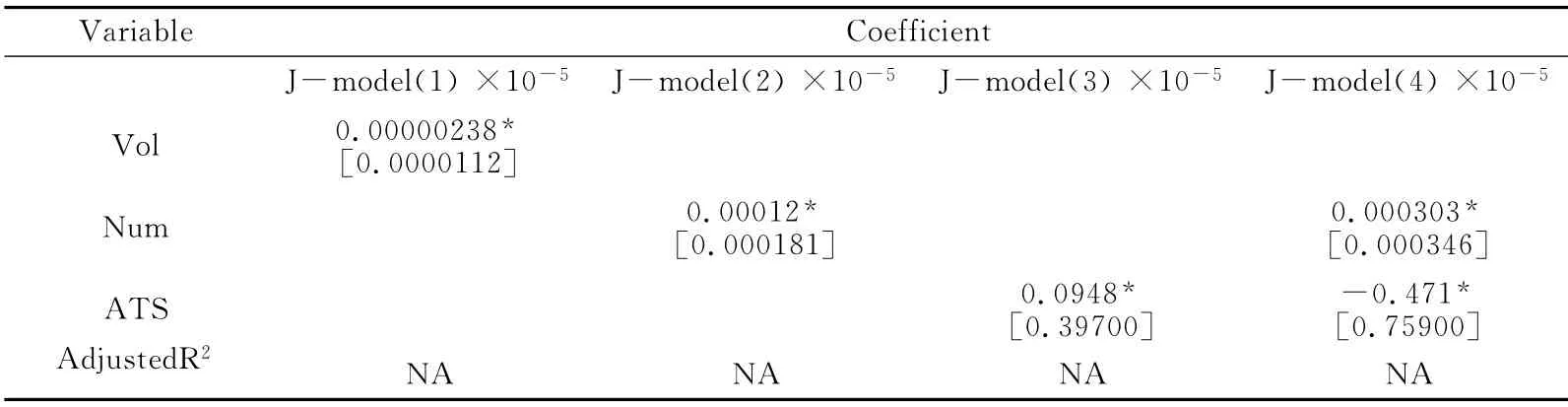
表5 跳躍波動量價關系模型估計結果

3.量價關系非對稱模型估計

為了反映滬深300股指期貨市場價格上漲和價格下跌量價關系的變化，我們建立了相應的量價關系非對稱模型，并利用市場數據對模型進行了估計，結果如表6和表7所示。通過對成交量、成交次數及平均交易頭寸三個變量進行單獨估計的結果來看，三個變量對上偏已實現半方差和下偏已實現半方差都有著明顯的正向影響，但是它們對兩者的解釋力有著很大的差別。縱觀表6和表7所對應的Adjusted R2，下偏已實現半方差量價關系模型的調整擬合優度明顯大于上偏已實現半方差量價關系模型的擬合優度，這說明成交量、成交次數及平均交易頭寸等變量對下偏已實現半方差的解釋程度要高于上偏已實現半方差，也間接反映出下偏已實現半方差相對于上偏已實現半方差包含更多的波動信息，進一步證實了Potton和Sheppard［32］的研究結論，即下偏已實現半方差更適合用于對已實現波動率進行預測。另外，從各模型單獨估計情況來看，平均交易頭寸相比成交量和成交次數較好地擬合了已實現半方差的量價關系模型，且對已實現半方差的解釋程度最高，因此，平均交易頭寸實際上為滬深300股指期貨量價關系背后的主要驅動因子。

表6 上偏已實現半方差量價關系模型估計結果

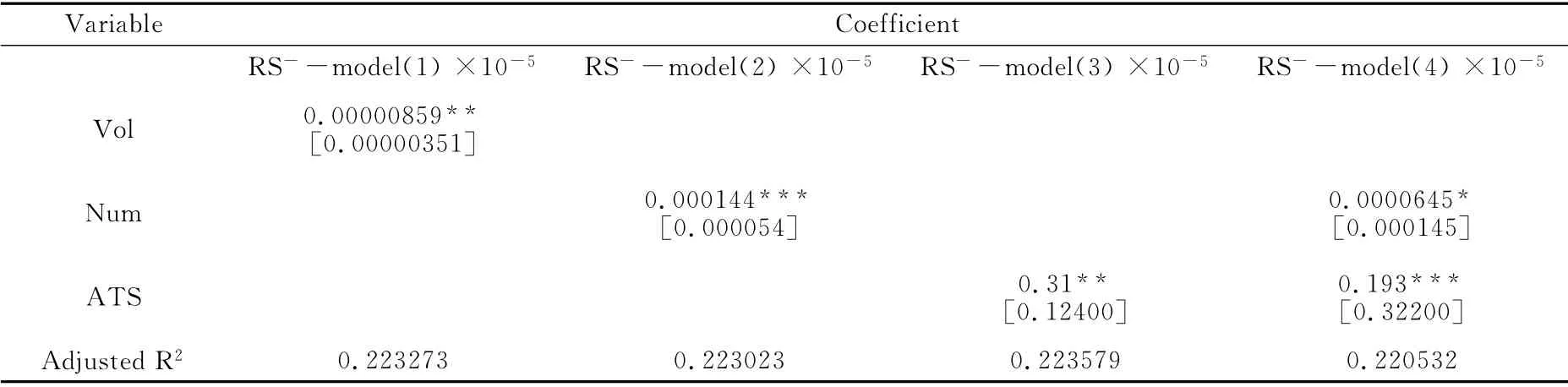
表7 下偏已實現半方差量價關系模型估計結果

四 結 論

（1）與中國股市一樣，滬深300股指期貨市場成交量與已實現波動率之間表現出明顯的正相關關系，即期指的波動伴隨著成交量的放大而不斷加大，伴隨著成交量的縮小而不斷減少。成交量、成交次數及平均交易頭寸等變量對期指的波動率有著正向的影響，能對市場波動做出一定程度的解釋，因此，它們在某種程度上都可以充當市場信息的代理變量。其中，平均交易頭寸相對成交量和成交次數而言，能夠更大程度地解釋期指市場已實現波動率，從而證實了標準的市場微觀結構理論，即平均交易頭寸包含了更多知情交易者的行為信息，市場波動大部分是知情交易者的買賣行為導致。

（2）滬深300股指期貨市場上成交量、成交次數及平均交易頭寸等變量對已實現波動率的連續和跳躍波動成分有著顯著的正向影響。連續波動成分包含更多價格波動的相關信息，利用連續波動的相關信息可以更為精確地對已實現波動率做出預測。成交量對連續波動的正向影響要明顯大于其對跳躍波動率的影響。因此，連續波動與成交量之間的正相關關系可以較為精確地反映滬深300股指期貨市場總的量價關系的變化。

（3）滬深300股指期貨市場的量價關系存在一定程度的非對稱性特征，主要體現在期指價格上漲和下跌過程中的波動信息含量不一樣，即下偏已實現半方差較上偏已實現半方差包含更多的已實現波動率信息；成交次數和平均交易頭寸的成交量信息含量不一樣，即平均交易頭寸較成交次數包含更多的市場信息。

（4）通過對三種量價關系模型的實證分析結果，我們發現平均交易頭寸比成交量和成交次數更好地擬合了量價關系模型，同時也更好地解釋了市場波動的相關信息，因此，平均交易頭寸實際為滬深300股指期貨市場量價關系背后的主要驅動因子，它可以作為期指市場新信息到達市場的代理變量。

［1］Crouch，R.L.The Volume of Transactions and Price Changes on the New York Stock Exchange［J］.Journal of Financial Analysts，1970，（26）：104－109.

［2］Karpoff，Jonathan M.The relation between Price Changes and Trading Volume：A Survey［J］.Journal of Financial and Quantitative analysis，1987，（1）：109－126.

［3］Gallant，A.R.，Rossi，P.E.，Tauchen，G.Stock prices and volume［J］.Review of Financial Studies，1992，（5）：199－242.

［4］陳怡玲，宋逢明.中國股票市場的價格變動與交易量關系的實證研究［J］.管理科學學報，2000，（2）：62－68.

［5］Clark P K.A Subordinated Stochastic Process Model with Finite Variance for Speculative Price［J］.Journal of Econometric，1973，（1）：135－155.

［6］Copland T E.A Model of Asset Trading under the Assumption of Sequential Information Arrival［J］.Journal of Finance，1976，（9）：1149－1168.

［7］Harris M.，Raviv A.Difference of Opinion Make a Horse Race［J］.Review of Financial Studies，1993，（6）：473－506.

［8］Wang J.A Model of Competitive Stock Trading Volume［J］.Journal of Political Economy，1994，（1）：127－168.

［9］Kyle，A.S.Continuous auctions and insider trading［J］.Journal of Econometrica，1985，（53）：863－894.

［10］Jones C.，Kaul G.，Lipson，M.Transactions，volume and volatility［J］.Review of Financial Studies，1994，（7）：631－651.

［11］Huang R.，Masulis R.Trading activity and stock price volatility：evidence from the London Stock Exchange［J］.Journal of Empirical Finance，2003，（10）：249－269.

［12］Chan，K.，Fong，W.M.Trade size，order imbalance，and the volatility－volume relation［J］.Journal of Financial Economics，2000，（57）：247－273.

［13］Easley D.，Kiefer N.，O’hara M.One day in the life of a very common stock［J］.Review of Financial Studies，1997，（10）：805－835.

［14］Chakravarty S.Stealth－trading：Which traders trades move stock prices？［J］.Journal of Financial Economics，2001，（61）：289－307.

［15］Chan K.，Fong W.Realized volatility and transactions［J］.Journal of Banking and Finance，2006，（30）：2063－2085.

［16］Giot P.，Laurent S.，Petitjean M.Trading activity，realized volatility and jumps［J］.Journal of Empirical Finance，2010，（17）：168－175.

［17］Chevallier J.，Sevi B.On the volatility－volume relationship in energy futures markets using intraday data［R］.Working Paper，2011

［18］張維，閆冀楠.關于上海股票市場價量因果關系的實證探測［J］.系統工程理論與實踐，1998，（6）：111－114.

［19］陳良東.上海股市價量關系的實證分析［J］.上海財經大學學報，2000，（3）：37－41.

［20］王承煒，吳沖鋒.中國股市價格—交易量的線性及非線性因果關系研究［J］.管理科學學報，2002，（2）：7－12.

［21］王杉，宋逢明.中國股票市場的簡單量價關系模型［J］.管理科學學報，2006，（4）：65－72.

［22］梁麗珍.分量回歸下的中國股市價量關系研究［J］.統計研究，2008，（12）：73－78.

［23］李夢玄，周義.基于高頻數據的中國股市量價關系研究［J］.財經論壇，2009，（3）：132－133.

［24］郭梁，周煒星.基于高頻數據的中國股市量價關系研究［J］.管理學報，2010，（8）：1242－1247.

［25］Andersen T.G.，Bollerslev T.，Diebold F.X.Roughing it up：including jump components in the measurement，modeling and forecasting of return volatility［J］.The Review of Economics and Statistics，2007，89：701－720.

［26］Barndorff－Nielsen O.，Kinnevrock S.，Shephard N.Measuringdownside risk—— Realised semivariance［A］.T.Bollerslev，J.Russell and M.Watson（Eds.）Volatility and Time Series Econometrics：Essays in Honor of Robert F.Engle［C］.2008，Oxford University Press.

［27］Andersen T.G，，Tim Bollerslev T.，Diebold F.The distribution of exchange rate volatility［J］.Journal of American Statistical Association，2001，（96）：42－55.

［28］Barndorff－Nielsen O.E.，Shephard N.Power and bipower variation with stochastic volatility and jumps［J］.Journal of Financial Econometrics，2004，（2）：1－37.

［29］Barndorff－Nielsen O.E.Econometrics of testing for jumps in financial economics using bipower variation［J］.Journal of Financial Econometrics，2005，（4）：1－30.

［30］Huang X.，Tauchen G.The relative price contribution of jumps to total price variance［J］.Journal of Financial Econometrics，2005，（3）：456－499.

［31］Anderson T.G.，D.Dobrev，and E.Schaumburg.Jump－robust volatility estimation using nearest neighbor truncation［R］.NBER Working Paper No.15533，2009.

［32］Patton A.，and Shapperd K.Good volatility，bad volatility：signed jumps and the persistence of volatility［R］.Working Paper，2011.