原子在界面附近自發輻射率的閉合軌道理論計算

王麗林， 徐 強， 隗 蓮

(1.山東鋁業職業學院 電氣工程系， 山東 淄博 255065； 2. 魯東大學 物理與電子工程學院， 山東 煙臺 264025)

原子所處環境對原子自發輻射的影響研究從20世紀40年代開始一直受到人們的關注[1-4].近年來，隨著實驗技術的進步和理論研究的深入，激發態原子的自發輻射率受介質環境的調制也已引起人們的廣泛關注.光子晶體熱潮的興起、微裝置捕陷作用以及應用場操縱高激發態原子的研究都極大地推動了對激發態原子的自發輻射率受環境調制問題的研究.用量子電動力學(QED)推導出的自發輻射率，看不出隨環境參數變化的規律.杜孟利等人利用閉合軌道理論對電介質層中以及電介質界面附近原子的自發輻射率的多周期振蕩進行了系統的研究，把閉合軌道理論中的電子擴展到了光子，獲得了成功[5-6].本文利用閉合軌道理論對環境中原子的自發輻射率的多周期振蕩的研究，在第一部分研究激發原子在一個無限大的金屬界面旁的自發輻射率,第二部分研究用兩個理想的金屬界面夾著的電介質中的原子的自發輻射率.

1 一個金屬界面旁的原子自發輻射

1.1 閉合軌道理論分析

閉合軌道理論最初是由杜孟利等人提出的，用來解釋強磁場中原子光吸收譜的振蕩現象[7].根據閉合軌道理論，當原子從高激發態躍遷到一個較低的態時，在原子附近輻射光子，光子以電磁波的形式向外出射，當電磁波向外傳播到離原子較遠處時可以近似由經典軌道來描述，當經典軌道族碰到界面后返回到原子附近，與這些軌道聯系的波與出射波干涉疊加可以在自發輻射率中形成一個振蕩.因為原子的自發輻射類似偶極天線的輻射，因此，本文考慮與自發輻射的一個經典的對應：偶極天線的輻射.

先看原子旁邊只有一個無限大的理想金屬面的情況，設金屬面與z軸垂直并位于距正z軸l處的地方，原子在x軸原點處(圖1).原子輻射出的光子沿著z軸作簡諧振蕩，它對應的電偶極矩為d0=de-iω0t，其中ω0為振蕩頻率，d0表示極化方向的單位矢量.它的輻射率為Wd=P/U，其中P為偶極天線的平均輻射功率，U為天線的能量.輻射率可以寫為

(1)

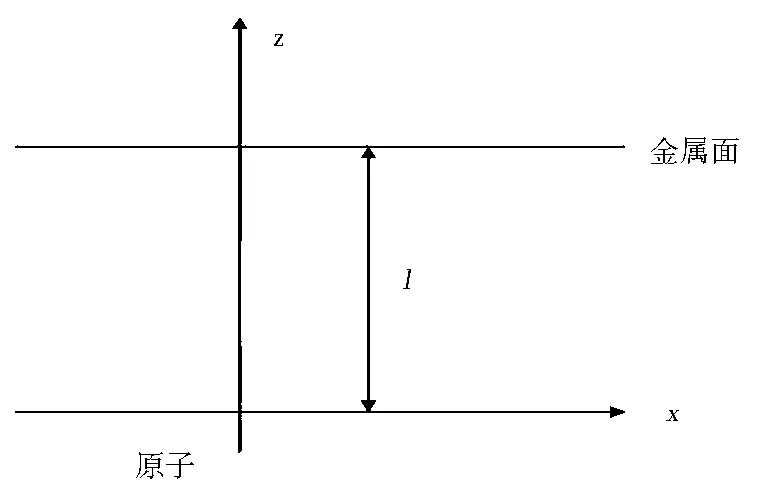
圖1 原子與金屬界面的距離是l

這里把振子附近的電場E分為兩個部分，出射部分E0和返回部分Eret.用r表示空間某點相對于偶極子的矢量位置，出射電場部分可以寫為

[d0-3r0(r0·d0)]×

(2)

返回電場Eret依賴于環境或偶極天線所在的介質.考慮偶極天線位于距理想金屬面l處且與金屬面平行的情況，由鏡像方法可以得到偶極天線處的返回電場為

(3)

1.2 平行情況(電偶極矩d與x軸夾角為0)分析

當原子對應的電偶極矩d與x軸方向平行時，即單位矢量d0與單位矢量r0夾角為90°時，根據閉合軌道理論,模擬偶極天線輻射，設理想金屬面的一邊是折射率為n的電介質，其中偶極子出射電場矢量位置r=2lr0，故這時原子的自發輻射率可以寫為

(4)

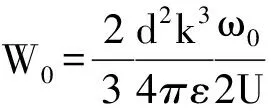
(5)

根據方程(5)，令理想金屬面的一邊是折射率n=1和n=1.49,利用maple軟件可以畫出相對自發輻射率Wd/W0隨原子與金屬界面距離l的變化圖(其中原子與金屬界面距離由無量綱參量a=l/λ0表示)，如圖2所示.

從圖2可以看出，相對自發輻射率表現為周期振蕩，隨著原子與金屬界面距離的增加，振蕩的振幅逐漸衰減.當原子離界面足夠遠時，自發輻射率接近于原子在真空中的自發輻射率.在折射率不同的介質中，周期振蕩也是有差異的.

1.3 垂直情況分析

當原子對應的電偶極矩d與x軸方向垂直時，即單位矢量d0與單位矢量r0夾角為0°時，根據閉合軌道理論,設理想金屬面的一邊是折射率為n的電介質，其中偶極子出射電場矢量位置r=2lr0，故這時偶極天線的輻射率可以寫為

(6)

令a=l/λ0，k0=2π/λ0，則式(6)變為

(7)

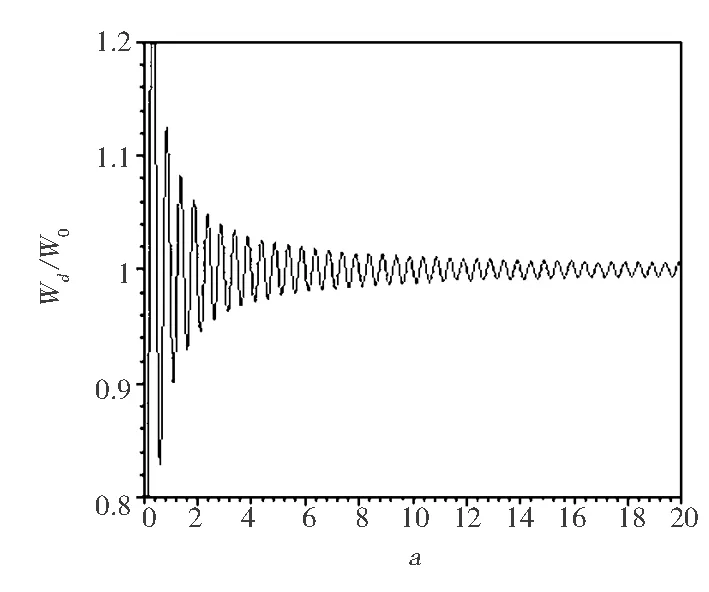
(a) 介質的折射率n=1

(b)介質的折射率n=1.49圖2 電偶極矩與x軸平行時相對自發輻射率隨原子與金屬界面距離的變化

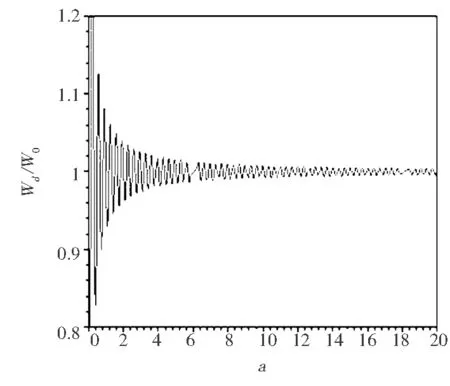
根據方程(7)，可以畫出理想金屬面的一邊是折射率n=1和n=1.49的相對自發輻射率隨原子與金屬界面距離的變化圖，如圖3所示.

從圖3可以看出，相對自發輻射率的周期振蕩類似于平行情況，但是在原子與金屬界面距離相同的情況時，垂直比水平的振蕩幅度大.

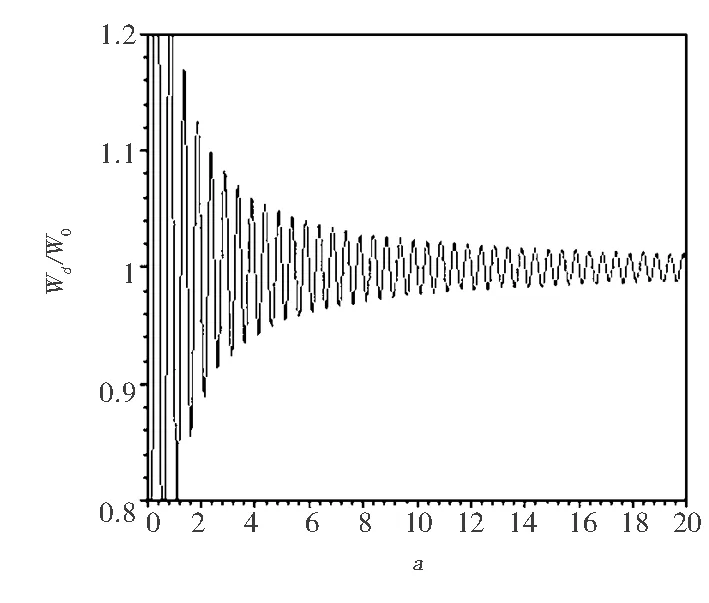
(a) 介質的折射率n=1

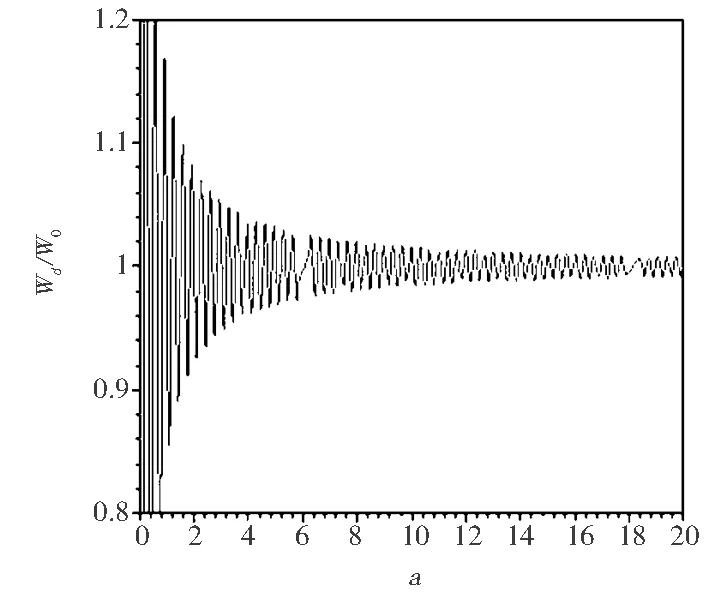
(b)介質的折射率n=1.49圖3 電偶極矩與x軸垂直時相對自發輻射率隨原子與金屬界面距離的變化

1.4 一般情況分析

當原子對應的電偶極矩d與x軸方向成任意角度θ(小于等于90°)時，即單位矢量d0與單位矢量r0夾角為(90°±θ)時，設理想金屬面的一邊是折射率為n的電介質，其中偶極子出射電場矢量位置r=2lr0，故這時原子的自發輻射率可以寫為

(8)

令a=l/λ0，k0=2π/λ0，則式(8)變形為

(9)

根據方程(9)，可以畫出理想金屬面的一邊是折射率n=1.49的相對自發輻射率隨原子與金屬界面距離的變化圖，其中還存在參量θ角，為了更明顯的從圖像上觀察結果，本文對θ取多個角度，如圖4所示.

從圖4可以看出，圖像均為周期性振蕩，大體情況與上面相似.在折射率n給定的情況下，隨原子對應的電偶極矩與x軸方向的角度增大，振蕩幅度增大.圖4(a)和圖4(d)分別與圖2(b)和圖3(b)比較可以看出角差不多大時，畫出的圖像差別較小.原子與金屬界面的距離和電偶極矩與x軸方向所成角度對自發輻射率都會產生較大影響.

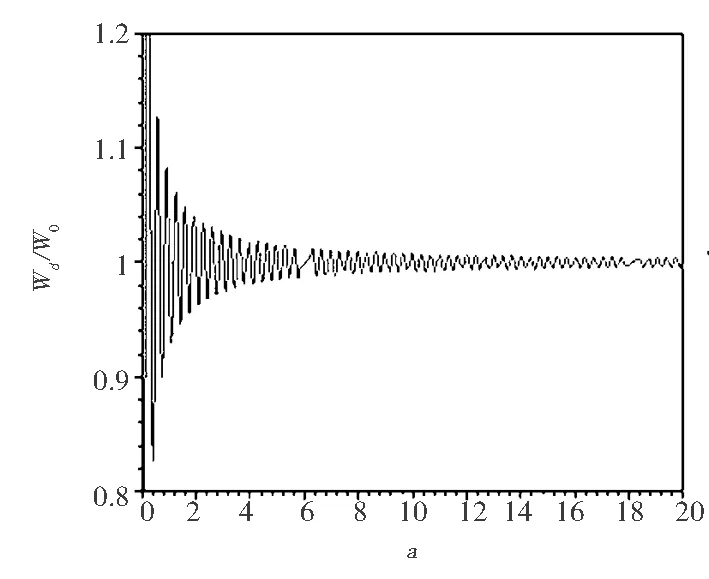
(a)θ=5°

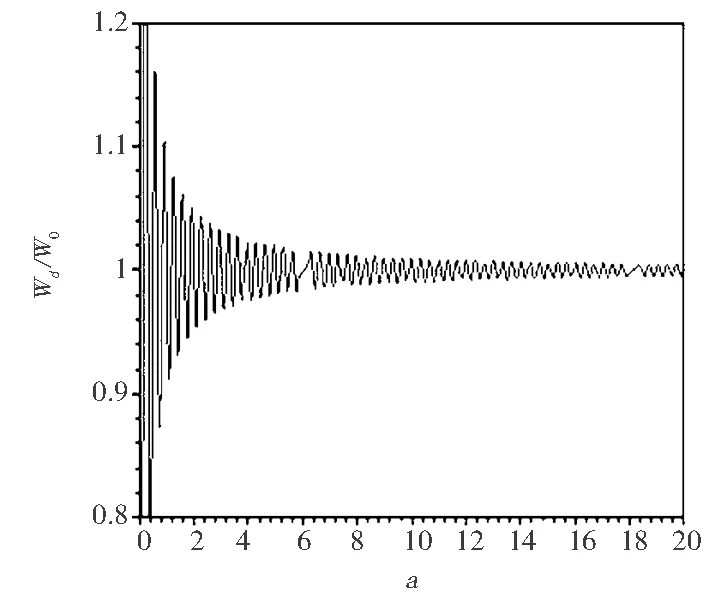
(b)θ=30°

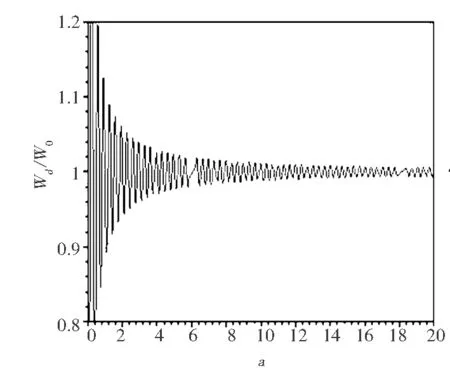
(c)θ=45°

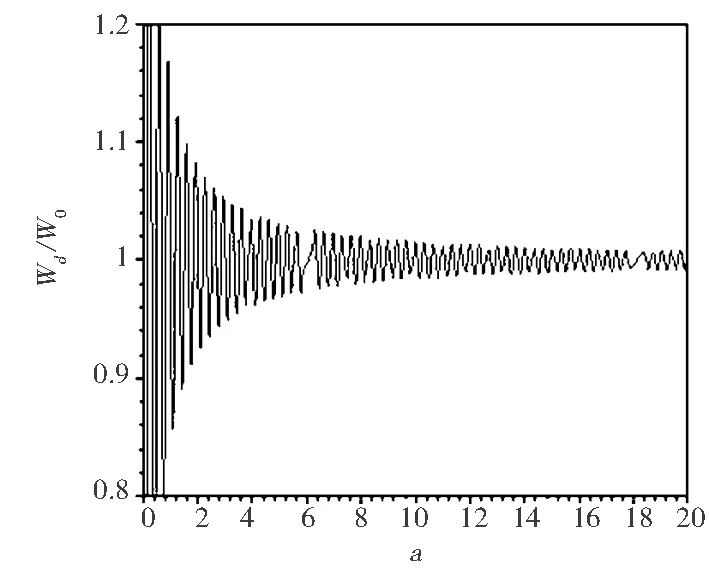
(d) θ=85°圖4 相對自發輻射率隨原子與金屬界面距離的變化(n=1.49)

2 兩個金屬界面旁的原子自發輻射

2.1 理論分析

在上述分析中我們已經得到一個金屬界面旁的原子自發輻射率，現在由此推廣到兩個金屬界面的情況.當原子對應的電偶極矩d與x軸方向平行時，一個金屬界面旁的原子自發輻射率為式(4).當偶極天線與金屬面之間的距離大于半個波長時，式(4)中的括號內的后兩項可以忽略不計，得

(10)

其中S=2nk0l為輻射光子從原子到金屬面再返回到原子的作用量，顯然這光子路徑為一個閉合軌道.現在通過圖像來比較一下理想金屬面的一邊是折射率n=1時,利用式(4)和式(10)畫出相對自發輻射率隨原子與金屬界面距離的變化圖，其中實線代表式(4)，虛線代表式(10)，如圖5所示.

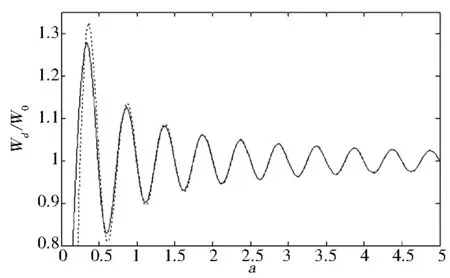
圖5 相對自發輻射率隨原子與金屬界面距離的變化(n=1)

由圖5看出，實線與虛線幾乎重疊，故式(4)與式(10)所得圖像相差很小，即(4)式括號內的后兩項可以忽略不計，所以一個金屬面前偶極子輻射率可以近似表達為式(10).

根據上述理論分析，把式(10)擴展到兩個金屬面間填充著同樣的電介質的情況，有

(11)

其中Sj=nk0Lj為第j個閉合軌道的作用量，Lj為該軌道的幾何長度；φj=-mjπ為相位修正，mj表示被金屬面反射的次數，式(11)即為閉合軌道理論公式.

2.2 公式推導

兩個平行的無限大的理想金屬板，板間填充折射率為n的非吸收性介質，自發輻射原子處于介質中.設選取坐標原點在發射原子處，z軸與金屬板垂直，原子在介質中相對與兩金屬板的距離分別為l1和l2，介質的厚度為l=l1+l2.如圖6所示.

為了方便計算兩個平面平行金屬板間原子的自發輻射率，只考慮偶極距d平行于金屬板的情況，則采用式(11).根據閉合軌道理論，在此種情況下存在四個基本的閉合軌道，如圖7所示.

其中四個軌道的作用量分別為S1=2nk0l1，S2=2nk0l2，S3=S4=2nk0l，四個相位修正分別為φ1=φ2=-π，φ3=φ4=-2π，代入式(11)可得原子自發輻射率為

(12)

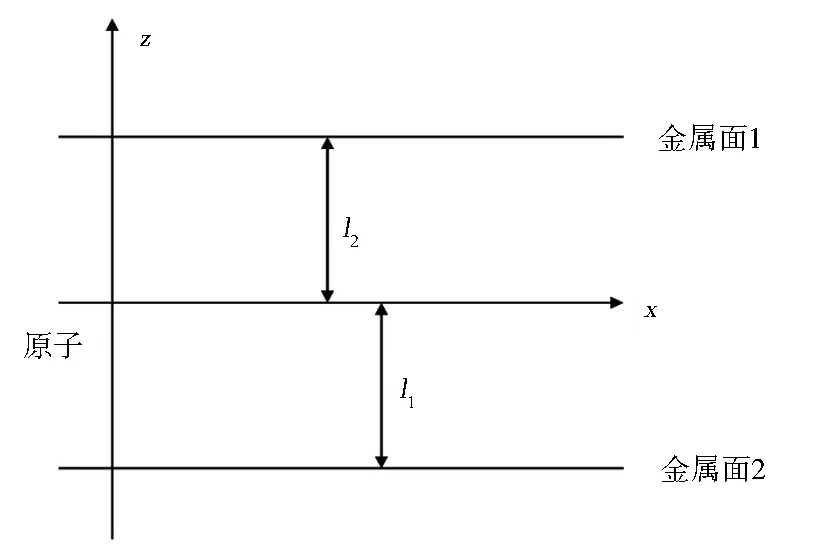
圖6 原子距離金屬界面的距離分別為l1、l2

圖7 原子在兩金屬界面間的四個基本的閉合軌道

為方便研究自發輻射率中的多周期振蕩，定義R=(l2-l1)/(l2+l1)用以標記原子相對于上下的金屬板的位置，定義兩個金屬板間的標準距離為l0=λ0=2π/k0，即輻射光子在真空中的波長，同時定義標度變量表示整個體系的大小變化，金屬板間的距離則為l=al0.簡單的幾何關系給出原子與上金屬界面距離以及原子與下金屬界面距離的關系分別為l1=a(1-R)l0/2和l2=a(1+R)d0/2.在給定R后，就可以給出自發輻射率作為自變量為空間標度變量a的函數，由式(12)可得

(13)

2.3 結果分析

在兩平行平面金屬板界面中填充折射率為n的電介質時，原子的自發輻射率公式由閉合軌道理論已經得出，其中標度變量a與原子到金屬板界面的距離有關.因此，在R和折射率n給定時，根據式(13)就可以畫出原子相對于金屬界面在不同位置時相對自發輻射率隨標度變量a的變化.現在令折射率n=1.49，原子相對位置分別為R=0，1/3，1/2，3/5，3/4，4/5時，畫出圖像如圖8所示.

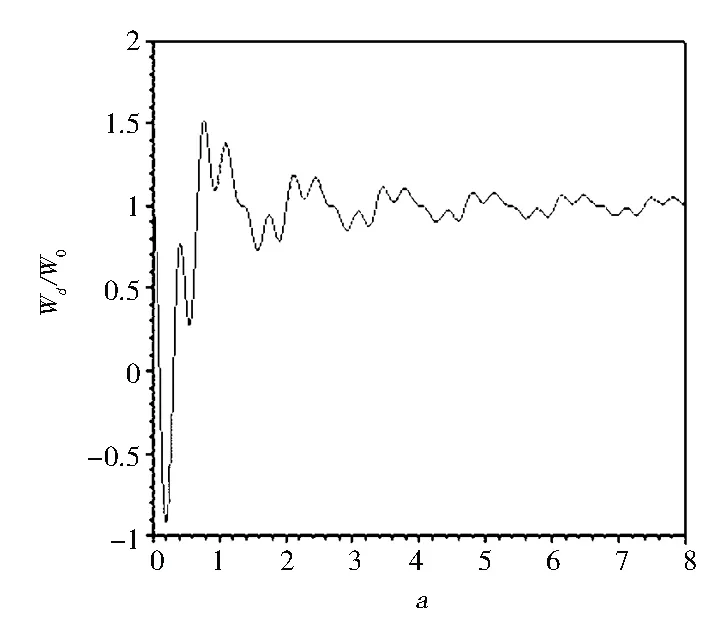
(a) R=0

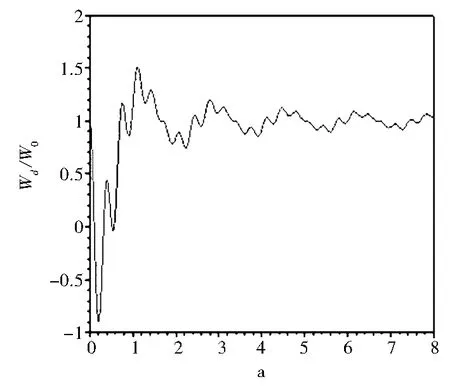
(b) R=1/3

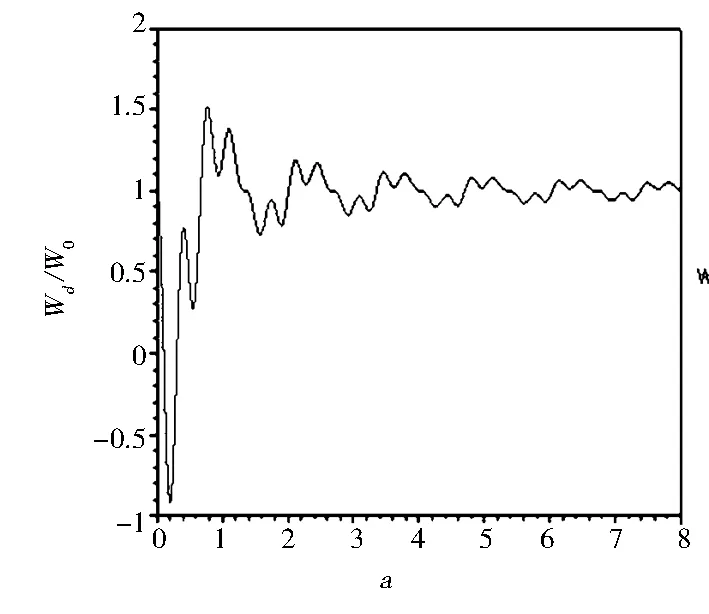
(c) R=1/2

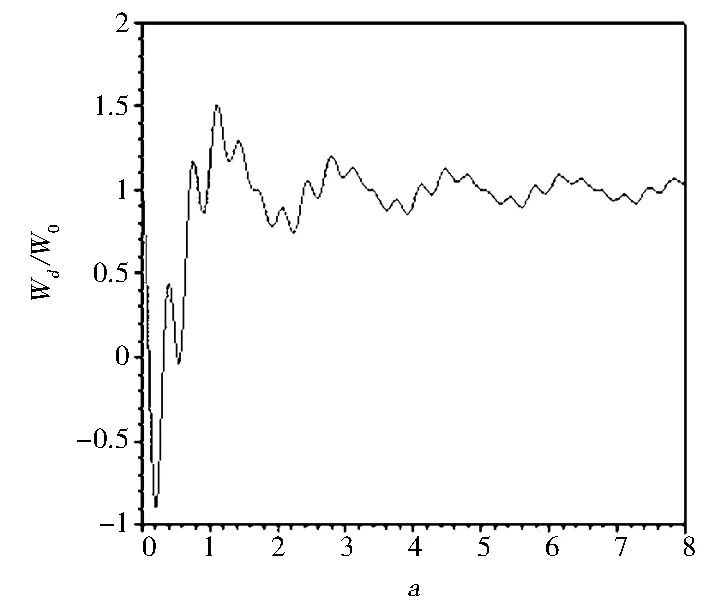
(d) R=3/5

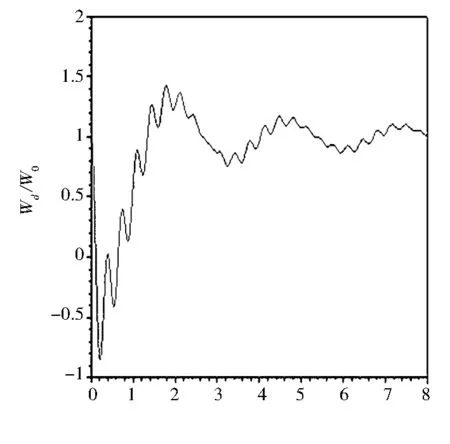
(e) R=3/4

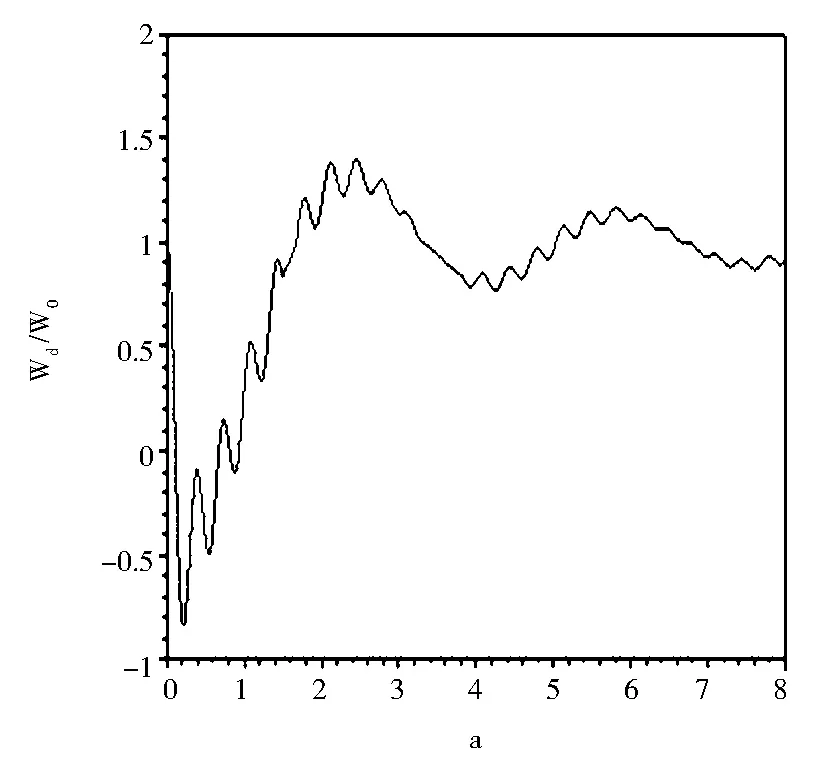
(f) R=4/5圖8 原子相對于金屬界面在不同位置時相對自發輻射率隨標度變量的變化(n=1.49).

從圖8可以看出，在圖8(a)中輻射原子位于介質中點，輻射率表現為衰減的鋸齒狀振蕩.圖8(b)中原子距離上邊的金屬板為介質厚度的1/3，自發輻射率中一些高頻振蕩出現.余下的4幅圖像顯示，隨原子距離上邊金屬板距離的增大自發輻射率中一些高頻振蕩逐漸增多，該周期振蕩的中心是1.0，即為真空中的自發輻射率.在圖中有許多峰出現，當R=0時，原子位于介質中點所以每個峰對應兩個閉合軌道，當原子不在兩個金屬板的中間位置時，有一些峰的簡并被解除，有一些被保留下來.

3 結束語

根據經典偶極天線的輻射情況，通過引入位置的標度變量，討論了一個金屬界面旁的原子自發輻射對激發態原子自發輻射率的影響，并將原子自發輻射率的結果在推廣到兩個金屬界面旁的情況.研究表明，隨著激發態原子位置的變化，自發輻射率呈現復雜的多周期振蕩，輻射出的光子經界面反射后返回到原子上，與出射的光子相干,從而抑制或加速激發態原子的自發輻射.自發輻射率的振蕩與光子的閉合軌道相對應，正是這種多周期的光子閉合軌道貢獻的迭加，原子的自發輻射率呈現復雜的振蕩特性.

[1]Philpott M R. Fluorescence from molecules between mirrors [J]. Chem.phys.Leet, 1973, 19(3): 435-439.

[2]Milonni P W,Knight P L. Spontaneous emission between mirrors[J]. Opt.Commun, 1973, 9(2): 119-122.

[3]Kleppner D. Inhibited spontaneous emission[J]. Phys.Rev.Lett, 1981, 47(4): 233-236.

[4]Goy P, Raimond J M, Gross M,etal. Observation of cavity-enhanced single-atom spontaneous emission[J]. Phys.Rev.Lett, 1983, 50(24): 1903-1906.

[5]Wang F H, Jin Y P, Gu B Y,etal. Application of closed-orbit theory to the spontaneous emission of atoms near a single dielectric interface[J]. Phys.Rev.A, 2005, 71(4): 044901-8.

[6]Du M L, Wang F H, Jin Y P ,etal. Oscillations in the spontaneous emission rate of atoms in a dielectric slab:Effects of photon closed orbits [J]. Phys.Rev.A, 2005,71(6): 065401-7.

[7]Du M L,Delos J B. Effect of closed classical orbits on quantum spectra:Ionization of atoms in a magnetic field[J]. Phys.Rev.Lett, 1987,58(17): 1731-1733.