基于社會網絡分析的網絡輿論系統狀態研究

楊勇 薛振中

(武警警官學院，四川 成都610213)

1 引言

隨著近年來互聯網在我國的快速發展，基于互聯網領域的群體性事件迅猛發展，影響范圍不斷加大。現實社會中的大量群體性事件由網絡醞釀產生，并不斷與網絡產生互動，同時少數別有用心的人趁機煽動作亂，大量的網民盲目參與形成了難以控制的不安定局面，給黨和政府對事件的妥善處置造成了干擾和壓力。因此，深入研究與網絡群體性事件密切關聯的網絡輿論系統，為下一步制定有效的防范策略帶來新的思路，具有重要意義。

作為發展中的復雜系統學的一部分，國外一般把輿情形成與演化原理的研究劃歸于輿情動力學(Opinion Dynamics)范疇。從20世紀50年代Bibb Latané提出的社會影響理論(Social Impact Theory)開始，具有代表性的輿情動力學模型有:Sznajd模型(SM)、投票人模型(The Voter Models)、妥協模型(Relative Agreement)、多數準則模型(The Majority Rule Models)、Axelrod模型(又稱文化模型)、受限信任模型(Bounded Confidence Model，BCM)等［1-6］。這些模型的研究對象主要是傳統輿論，多數都使用基于主體的建模方法(Agent-Based Modeling)。但由于網絡輿論系統的復雜性與社會性等特征，以規則確定行為的傳統社會動力學原理難以適用。社會網絡分析(Social Network Analysis，SNA)方法用社會網絡結構對行動的限制來解釋行為，是一種研究社會成員或群體之間的相互作用關系的有效方法。它將系統成員或成員群體間的關系作為研究對象，利用關系模型的特征參數進行量化分析，將定性研究與定量研究結合起來，比傳統的定性研究更具優勢。這一方法經過七十余年的反復驗證和逐步完善已經成熟，已廣泛用于社會學、心理學和經濟學等學科領域的研究。

2 基于SNA的網絡輿論系統狀態參數差分法

通過對網絡整體及網民主體的SNA屬性參數組的差分計算獲得網絡輿論系統狀態分布的變化量，通過差分量的時間序列展開觀測狀態變化是否符合預期，發現對狀態分布和變化起主導作用的意見領袖，挖掘出網絡輿論系統演化特征并對其進行定量分析，可以揭示出網絡輿情事件的一般演化規律。

2.1基本步驟

(1)針對某一話題或某一關鍵詞對關注中的網站或論壇進行數據采集，將采集到的數據進行初步的去噪消重處理，找出網民之間的回復關系，存入數據庫。

(2)根據網絡輿論持續時間或者狀態觀測者的要求設定觀測周期Δt，該觀測周期可隨時進行調整。讀取數據庫中的數據，建立每個觀測周期內的回復關系矩陣并繪制出網絡社群圖。

(3)根據網絡社群圖，計算出每個觀測周期的SNA參數值。

(4)將每個觀測周期的SNA參數值按時間序列展開，利用差分法計算每個觀測周期內的SNA參數增量。

(5)對計算出的SNA參數增量進行綜合分析研究，揭示出該網絡輿論的特征。

2.2 網絡輿論主體的狀態分析

2.2.1 點度中心度與中心性

中心性是指個人或組織在其社會網絡中具有怎樣的權利，或者說居于怎樣的中心地位。點度中心度是識別意見領袖的重要指標。一般認為，在網絡中點度中心度最大的網民為該話題的意見領袖。

定義1 絕對點度中心度CADi，為與結點i有直接聯系的結點數目，即與該網民發生直接聯系的網民數目，主要反映該網民的影響范圍。

定義2 相對點度中心度CRDi，為結點i的絕對點度中心度與圖中點的最大可能度數之比，即與該網民實際發生直接聯系的網民數目與最大可能發生直接聯系的網民數目之比。在單向連接中的計算公式為:

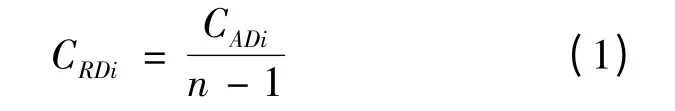
式(1)中，n為網絡結點數，即網民數。CRDi以CADi為基礎，主要反映該網民在整個網絡中的核心性，即地位的中心程度。

2.2.2 基于時間序列的狀態變化計算方法

設CADi(t)為t時刻網絡結點i的絕對點度中心度，則一個采樣周期Δt內CADi(t)的變化量為絕對點度中心度增量，記為ΔCADi(t)。

設CRDi(t)為t時刻網絡結點i的相對點度中心度，則一個采樣周期Δt內CRDi(t)的變化量為相對點度中心度增量，記為ΔCRDi(t)。

2.2.3 狀態分析

記Δn(t)為網民數增量，當Δn(t)、ΔCADi(t)與ΔC'ADi(t)分別為正值、負值或0值時，其揭示出不同的網絡輿論特征。下面將上述三個參數值簡化為非負值與負值兩種情況，分別進行研究，結果見表1。

對Δn(t)、ΔCRDi(t)與ΔC'RDi(t)分非負值與負值兩種情況進行研究，結果見表2。

2.3 網絡輿論系統的狀態分析

表1 絕對點度中心度相關參數變化含義

表2 相對點度中心度相關參數變化含義

2.3.1 網絡密度

網絡密度表示網絡社群圖中各個結點間聯絡的稀密程度。在網絡輿論系統中，結點表示發帖或跟帖的網民，結點間的連線表示網民間的帖子跟隨關系，網絡密度則反映出網民之間相互跟帖關系的密集程度。計算公式為:

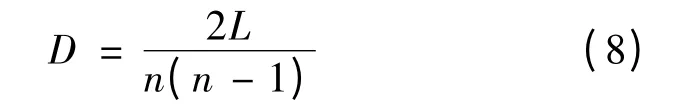
式(8)中，n為網絡結點數，即網民數;L為所有結點間實際擁有的連線數。

2.3.2 網絡中心勢

網絡中心勢以點度中心度為基礎，刻畫網絡社群圖的整體中心性，用來測量整個網絡的連通情況對少數行為者的依賴程度。在網絡輿論系統中用來測量信息流在整個網絡的傳播情況對少數網民的依賴程度。網絡中心勢反映的是網絡社群圖的整體向心程度，在網絡輿論系統中則反映出其他網民對某一網民回應的集中程度。網絡中心勢越大，說明該話題的討論集中程度越大，意見領袖具有的凝聚力越大，產生影響力較大的意見領袖的可能性越大。其數學表達式為:

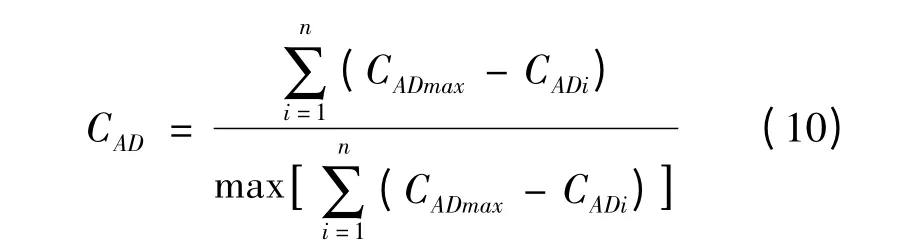
由于當且僅當網絡為包含n個結點的星形結構時，除數達到最大值n2-3n+2，因此，式(10)可以簡化為:

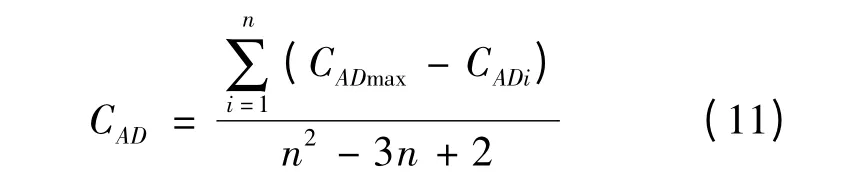
2.3.3 基于時間序列的狀態變化計算方法

設D(t)為t時刻的社會網絡密度，則一個采樣周期Δt內D(t)的變化量為密度增量，記為ΔD(t)，ΔD(t)∈［-1，1］。

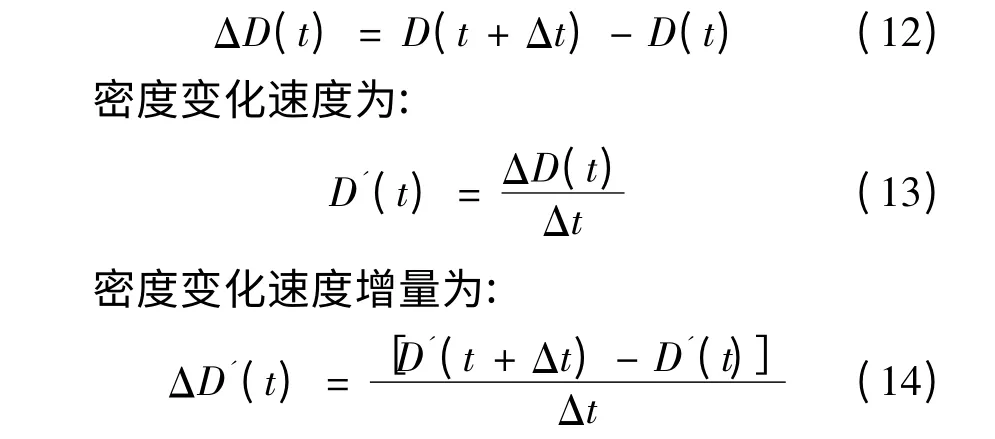
設C(t)為t時刻的社會網絡中心勢，則一個采樣周期Δt內C(t)的變化量為網絡中心勢增量，記為ΔC(t):

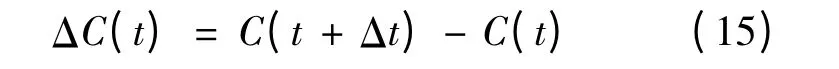
網絡中心勢變化速度為:

2.3.4 狀態分析

記Δn(t)為網民數增量，當Δn(t)、ΔD(t)與ΔD'(t)分別為正值、負值或0值時，其揭示出不同的網絡輿論特征。下面將上述三個參數值簡化為非負值與負值兩種情況，分別進行研究，結果見表3。

對Δn(t)、ΔC(t)與ΔC'(t)分非負值與負值兩種情況進行研究，結果見表4。

將ΔCADi(t)、ΔCRDi(t)、ΔD(t)和ΔC(t)稱為SNA參數增量，將Δ(t)、Δ(t)、ΔD'(t)和ΔC'(t)稱為SNA參數變化速度增量。一般而言，若網民數增量與SNA參數增量均大于0，說明網絡輿論處于形成或發展時期，網絡輿論具有進一步發展甚至爆發的可能，此時應予以重點關注;若網民數增量與SNA參數增量均小于0，則說明網絡輿論處于回落或冷卻時期，將逐漸退出公眾的視野;若網民數增量、SNA參數增量與SNA參數變化速度增量在正負值之間圍繞0波動，則說明參與者相互關系的密集程度和討論的熱烈程度有波動，網民對話題的關注度可能偏移或轉移，網絡輿論處于起伏狀態，可能演變至偏移期或振蕩期。

3 實驗驗證

以天涯論壇(www.tianya.cn)的“華南虎事件”為實驗數據(該事件源于網絡，并引發現實社會的大量關注)，運用SNA理論及其參數差分法，通過網絡數據采集與分析系統實現對網絡輿論狀態觀測方法的仿真。

3.1 實驗數據

在2007年底至2008年初，華南虎事件是社會輿論的熱點話題。該事件是網絡輿論從發生、發展到爆發直至消亡的典型案例。據統計，該話題在天涯論壇上的總參與人數為5779人，總回帖數65029個，持續時間自2007年10月15日樓主發帖開始，直至2008年1月30日最后一位跟帖者發帖結束，經歷了從形成、發展、爆發直至回落的主要演變過程。將回帖采集并經初步處理后存入數據庫中，設定采樣周期為1天，按天統計網民數，如圖1所示。

表3 社會網絡密度相關參數變化含義

表4 網絡中心勢相關參數變化含義

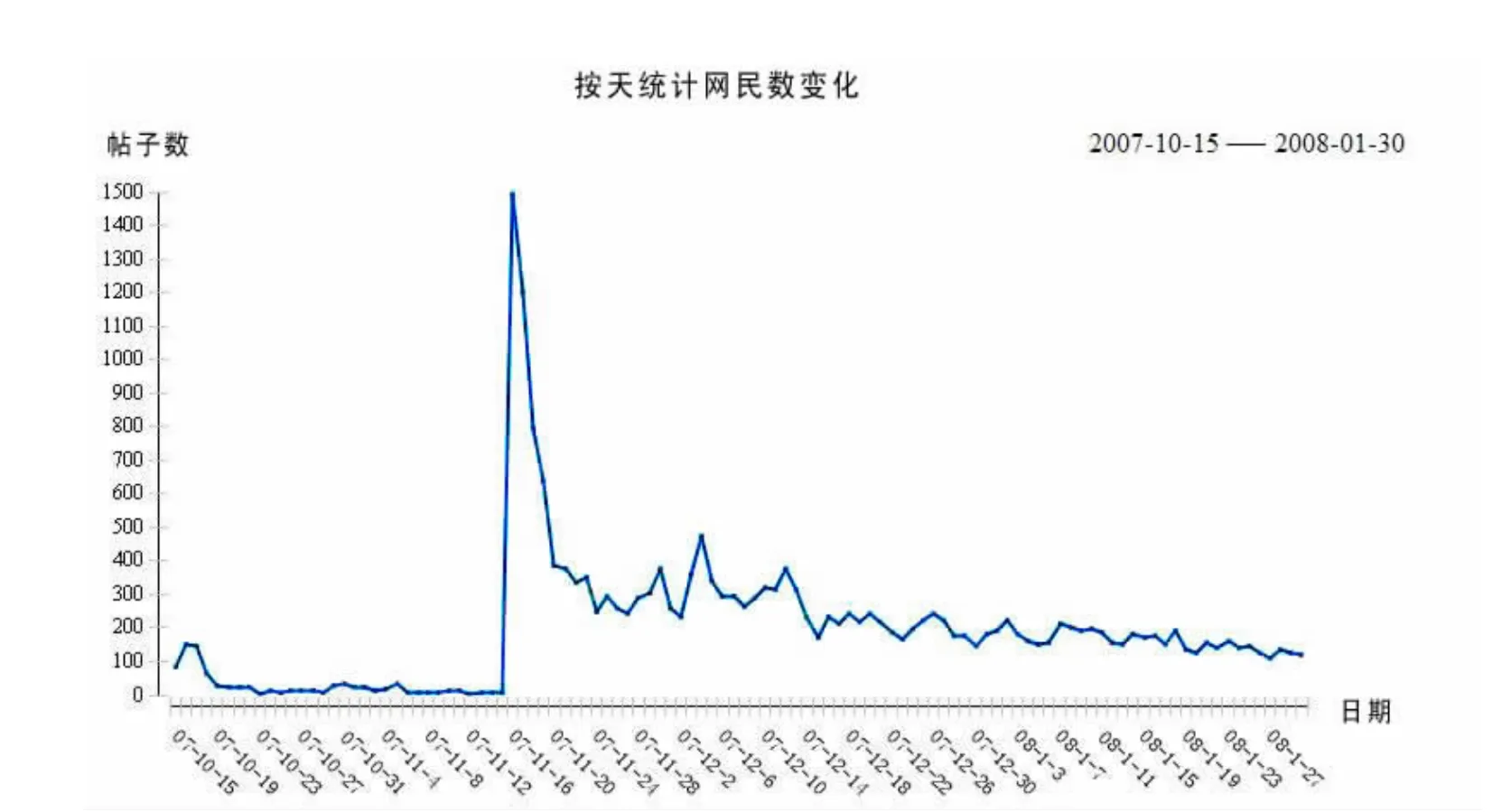
圖1 天涯論壇“華南虎事件”輿論演變圖

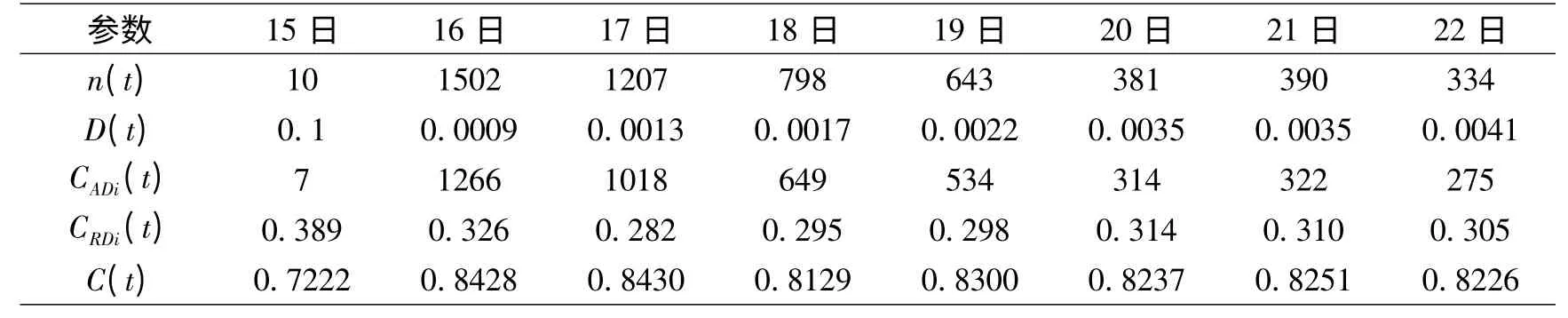
表5 SNA參數表(8天)

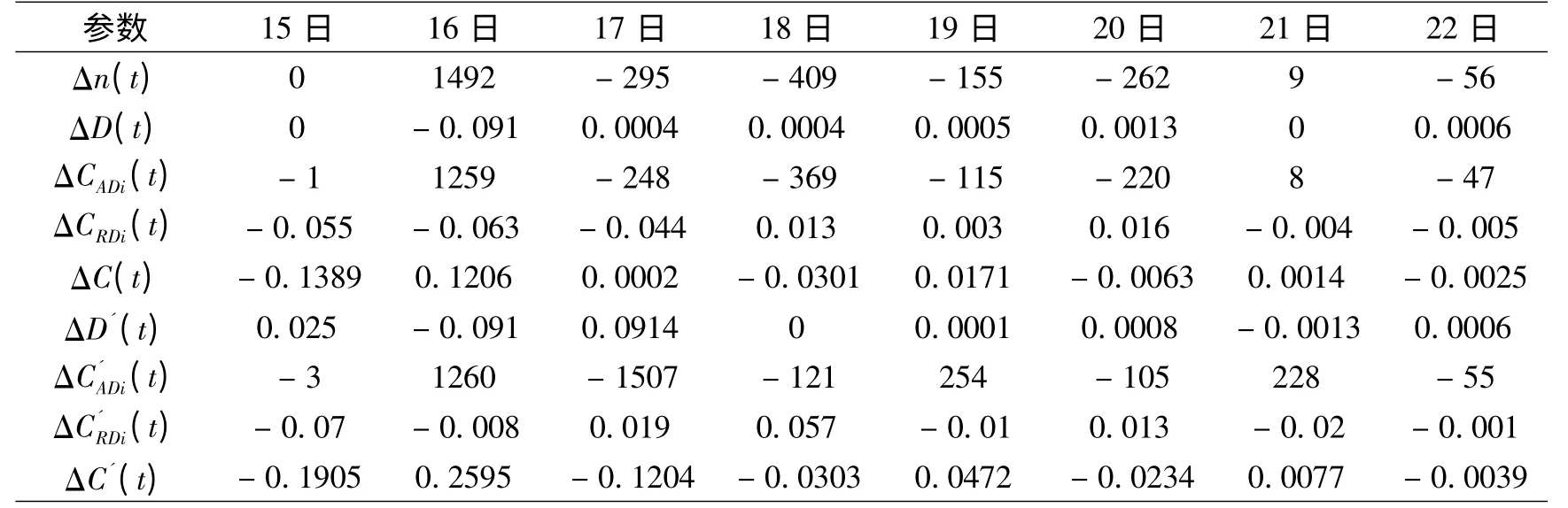
表6 SNA參數增量表(8天)

3.2 數據分析

將參與天涯論壇“華南虎事件”討論的網民及其之間的聯系看作是一個網絡輿論系統。使用SNA方法進行數據分析，得到SNA參數值見表5(限于篇幅，僅截取11月15日—22日共8天數據)，其中CADi(t)、CRDi(t)分別為意見領袖的絕對點度中心度和相對點度中心度。通過分析這些參數值就可以了解到該網絡輿論系統的主要特征。

根據上述SNA參數值，采用差分分析法計算其增量，見表6。

3.3 結論

通過數據分析，可以得出以下結論。

(1)11月16日，網民數量達到最大值，說明此時參與該話題討論的人數最多，可認為是討論最熱烈的時刻。ΔCADi(t)與ΔC'ADi(t)也在同時達到最大值，這是符合預期的，體現出參與討論的網民對于樓主的回復十分熱烈且這種趨勢大幅上升。但此時ΔCRDi(t)與Δ(t)為負，說明隨著參與討論的網民數量的增多，并非所有參與討論的網民都回復樓主，網民之間也產生了一些討論與交流，形成了一些小團體，即所謂的凝聚子群。在這些凝聚子群中，也有各自的意見主導者，隨著輿情事件的演變，有成長為新意見領袖的可能。ΔC(t)與ΔC'(t)也達到最大值，說明當前時刻對于該話題的討論集中程度大，當前意見領袖的凝聚力和影響力大，且這種趨勢大幅上升。另一方面，由于參與網民數量激增，網民之間討論交流不夠充分，相互關系的密集程度大大減小，導致ΔD(t)大幅下降，但這種趨勢有所下降。

(2)11月17日—24日，參與網民數量逐漸減少，輿情事件在經過爆發后開始回落。ΔCADi(t)為負值，說明討論人數持續減少;Δ(t)出現最小值后圍繞0值波動，說明這種趨勢在大幅震蕩后逐漸趨于平緩，這是輿情事件進入回落階段的標志之一。ΔCRDi(t)與Δ(t)、ΔC(t)與ΔC'(t)均圍繞0值小幅波動，說明網民之間討論與交流更加熱烈，趨勢也有所反復。參與網民不再是單純回復樓主，其間形成了一些凝聚子群，根據凝聚子群中意見主導者地位及其凝聚力和影響力的變化，樓主的意見領袖地位及其凝聚力和影響力也隨之波動。ΔD(t)與ΔD'(t)在快速回落后基本保持不變，說明輿情事件在經過短暫的爆發期后，參與網民相互之間對該話題討論的密集程度基本不變，趨勢也基本保持穩定。

(3)11月25日—12月13日，網民數量保持穩定，這些網民是該話題較為穩定的參與者和討論者。同時，ΔCADi(t)與Δ(t)、ΔD(t)與ΔD'(t)也保持穩定，這是輿情事件進入平穩階段的標志之一。但是，ΔCRDi(t)與Δ(t)、ΔC(t)與ΔC'(t)均出現較大幅度的波動，說明網民間的討論與交流仍然十分熱烈，趨勢也有較大幅度的變化，隨時都有再次爆發或形成新意見領袖的可能，該輿情事件仍具有一定的生命力。

可見，通過對SNA參數增量與SNA參數變化速度增量的綜合分析，能夠在一定程度上揭示出網絡輿論系統的深層次特征。

4 結束語

本文僅從系統整體的角度，借助SNA理論對網絡輿論系統進行了研究，其中的許多細節尚有待進一步深入研究，如:網民主體的相關屬性、網絡輿論系統的相關屬性、網絡輿論系統的指標體系等。

1 SZNAJD WERON K，SZNAJD J.Opinion evolution in closed community［J］.International Journal of Modern Physics C，2000，11(6):1157-1165.

2 PETER CLIFFORD，AIDAN SUDBURY.A model for spatial conflict［J］.Biometrika，1973，60(3):581-588.

3 DEFFUANT G，NEAU D，AMBLARD F，et al.Mixing beliefs among interacting agents［J］.Adance in Complet Systems，2001(3):87-98.

4 GALAM S.Minority opinion spreading in random geometry［J］.Eur.Phys.J.B，2002，25(4):403-406.

5 AXELROD R.The dissemination of culture:A model with local convergence and global polarization［J］.Journal of Conflict Resolution，1997，41(2):203-226.

6 HEGSELMANN R，KRAUSE B U.Opinion dynamics and bounded confidence models，analysis，and simulation［J］.Journal of Artificial Societies and Social Simulation，2002，5(3):1-33.

7 STAUFFER D，SOUSA A O，OLIVEIRA S M.Generalization to square lattice of Sznajd sociophysics model［J］.International Journal of Modern Physics C，2000，11(6):1239-1245.

8 BERNARDESA T，STAUFFER D，KERTFFESZJ.Election results and the Sznajd model on Barabasi network［J］.European Physical Journal B，2002，25(1):123-127.

9 GONZALEZ M C，SOUSA A O，HERRMANN H J.Opinion formation on a determinstic pseudo-fractal network［J］.International Journal of Modern Physics C，2004，15(1):45-57.

10 FORTUNATO S.The Krause Hegselmann consensus model with discrete opinions［J］.International Journal of Modern Physics C，2004，15(7):1021-1029.

11 HOLME P，NEWMAN M E J.Nonequilibrium phase transition in the coevolution of networks and opinions［J］.Physical Review E，2006，74(5):1-5.

12 KOZMA B，BARRAT A.Consensus formation on adaptive networks［J］.Physical Review E，2008，77(1):6102-6114.

13 張立，劉云.網絡輿論傳播的無標度特性及其衰減模型的研究［J］.北京交通大學學報:自然科學版，2008，32(2):67-70.

14 曾祥平，方勇，袁媛，等.基于元胞自動機的網絡輿論激勵模型［J］.計算機應用，2007，27(11):2686-2688，2714.