基于能量法計算材料的彈性模量和壓痕硬度

金宏平，陳建國

（湖北汽車工業學院機械工程系，十堰442002）

0 引 言

很長時間以來，在實際工程中常將硬度作為評估材料強度、耐磨性和剛度的一個指標。但是，由于傳統的硬度測試要求用光學儀器測量殘余壓痕的尺寸，這使其在工業應用中存在一定困難，并容易引起誤差。最近十多年以來，由于新材料的大量涌現，特別是納米材料和涂層材料在工程中的大量應用，為了評價這些新材料的力學性能，常規的力學性能測試方法顯然已不適用。因此，很多學者嘗試通過分析硬度測試過程中的載荷和位移數據，建立載荷-位移曲線與材料性能之間的某種約束關系，如圖1所示，從而間接獲得材料的力學性能［1-5］。

Oliver和Pharr［6］等通過研究拋物面形狀壓頭的接觸深度、壓痕深度和卸載后殘余壓痕深度之間的關系，根據彈性理論，提出了接觸深度hc的計算公式：

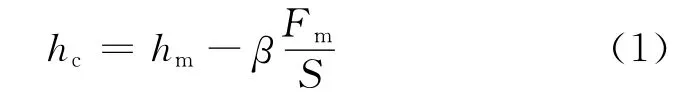
式中：hm為最大壓入深度；Fm為最大壓痕載荷；S為卸載斜率；β為與壓頭形狀有關的參數，對于球形壓頭，β＝0.75。

對于半徑為R 的球形壓頭，其壓痕硬度H 的計算公式為：

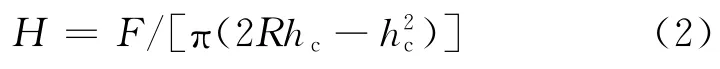
式中：F 為壓痕載荷。

由于Oliver-Pharr方法（簡稱O-P 法）快捷方便，易于實現，在工程上得到了廣泛應用，是現有商品化納米壓痕儀中計算壓痕硬度的通用方法。

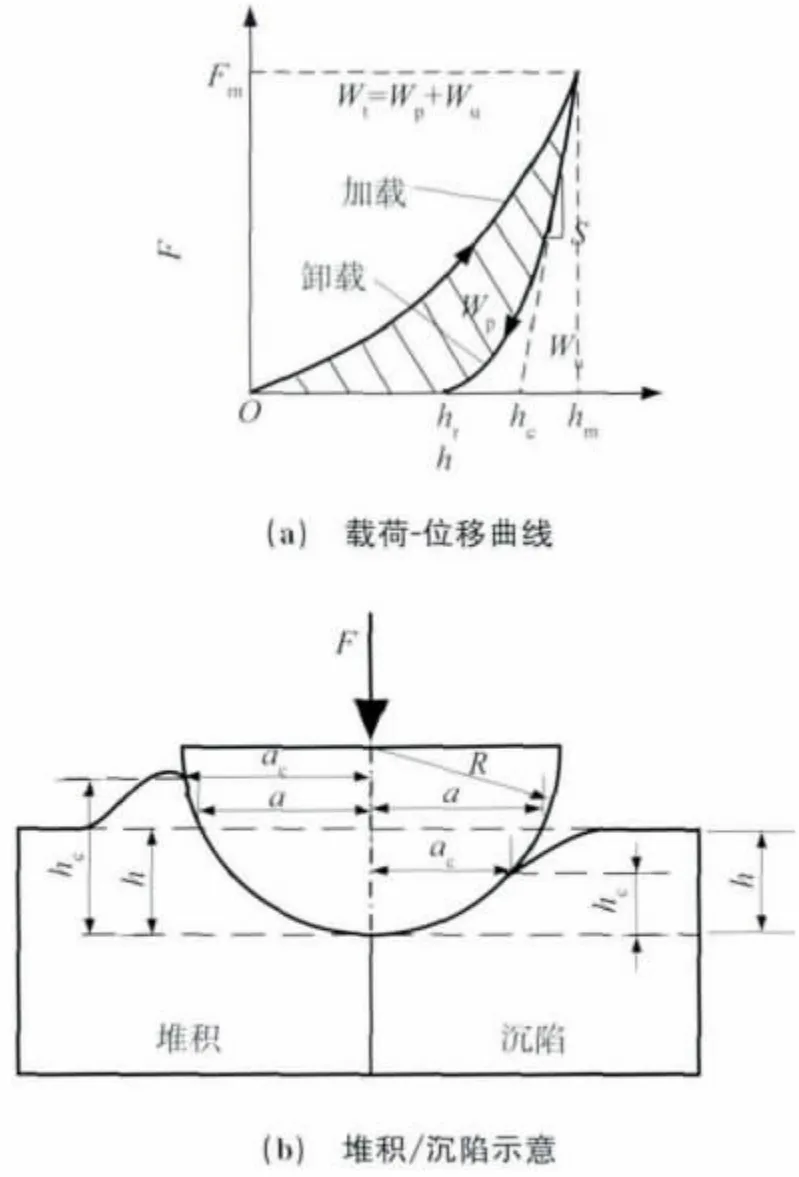
圖1 壓痕的載荷-位移曲線和堆積/沉陷示意Fig.1 Load-depth curves （a）and pile-up/sink-in sehematic of indentation（b）

對于彈塑性材料，最大壓痕載荷Fm和卸載斜率S 永遠是正值。由式（1）可知，接觸深度hc總是小于最大壓入深度hm，即在壓痕接觸邊沿總是呈現材料沉陷狀態，如圖1（b）右側所示。然而，在實際工程應用中并非都如此。……