基于不等式約束的顧及長度變形的坐標系統轉換方法

陶葉青，楊 娟

(宿州學院地球科學與工程學院，安徽宿州234000)

一、引 言

GPS的定位成果是基于WGS-84參考框架的，因此利用GPS技術建立或改善國家和地方坐標系的控制網需要將其定位成果轉換至國家或地方坐標系中。我國現行的參心坐標系統的點坐標是用二維或平面坐標與高程分開表示的，因而無法精確地用空間三維直角坐標表示出其點位坐標。因此，為實現GPS控制測量成果的坐標系統轉換，需將GPS定位成果的控制點間的空間三維坐標差(基線向量)表示為二維或平面坐標，這不可避免地會引起一定的長度變形，而相關的測量規范規定其變形值不應大于1/40 000［1］。為了減小由控制點間的空間距離轉換為平面距離過程中引起的長度變形，人們提出更改中央子午線或建立區域性橢球的方法［2-4］。應用這樣的方法所建立的坐標系更改了原有國家坐標系的基本投影與參考橢球的屬性，雖然減小了長度變形，但在GPS坐標系統轉換過程中，其最終轉換成果已不是國家或地方坐標系，且區域性橢球的算法不易于實現。此外，傳統的由數學轉換模型實現坐標系統轉換的方法并沒有顧及長度變形這一因素。

為將GPS控制測量的成果轉換至國家或地方坐標系中并顧及長度變形因素，擬將不等式約束應用至坐標系統轉換中。不等式約束問題的研究可追溯至40多年前，文獻［5］首先研究不等式約束的回歸分析;文獻［6-8］將不等式約束引入大地測量領域，并在變形檢驗、GPS數據處理、大地控制網的優化等方向取得了一定的應用成果;文獻［9-10］對不等約束的具體解法進行了研究;文獻［11］提出應用最優化計算理論中的罰函數方法實現不等式約束的平差算法。針對坐標系統轉換過程中不可避免地會出現長度變形的問題，應用不等式約束將長度變形量納入坐標系統轉換模型，進行平差處理。根據文獻［11］提出的不等式約束的平差算法，實現了能夠顧及長度變形的坐標系統轉換。

二、轉換方法與模型

坐標系統轉換常用的有七參數與四參數模型，以平面坐標系統轉換為例，通常采用的轉換模型為［12］

式中，a、b為兩個平移參數;α為旋轉參數;λ為尺度比參數;(x0，y0)、(x，y)為控制點在原坐標系(WGS-84坐標系)與目標坐標系中(國家坐標系)的平面坐標。應用GPS建立控制網進行坐標系統轉換時，若要獲得式(1)中控制點在原坐標系中的平面坐標，就需要將GPS的空間三維直角坐標轉換成大地坐標，并將大地坐標按高斯-克呂格投影至平面坐標。這一過程有兩個長度變形：①將空間三維直角坐標轉換成大地坐標，相應的空間距離轉換成橢球面大地線距離的長度變形;②將大地坐標轉換成平面坐標，相應的橢球面大地線距離轉換成平面距離的長度變形。長度變形對坐標系統的轉換有顯著的影響，但式(1)并不能夠顧及這方面的影響。

式(1)可表示成以(x，y)目標坐標為變量的函數模型

不等式約束的模型可表示為

式中，x表示目標坐標(x，y);B為轉換模型參數;l為原坐標(x0，y0)。

不等式約束的主要對象是控制點在實現坐標系統轉換后，對用平面坐標表示的長度變形量進行約束。相關規范一般要求根據控制點平面坐標反算距離與測距儀復測距離相對變形值小于1/40 000［1］。據此，約束不等式具體的形式為

式中，D為測距儀實測精度;(x1，y1)、(x2，y2)為目標坐標系中控制點的平面坐標。假設

式中，(x0，y0)為控制點在目標坐標系中的初始轉換值;(Δx，Δy)為其改正值;D0為根據初始值反算的初始距離。將控制點平面坐標表示的反算距離線性化為

因此，式(4)可表示為

式(8)為式(3)中二式的具體形式。不等式約束模型(式(3))可通過優化計算中的罰函數方法轉化為無約束最優化問題［11］

式中，VTPV=(Bx－l)TP(Bx－l)=min;P(x)為罰函數，它要求當參數x滿足式(3)中二式時，P(x)值取為零，不等式約束轉化為普通的最小二乘平差。當參數x不滿足式(3)中二式時，不等式約束轉化為等式約束進行計算。此時

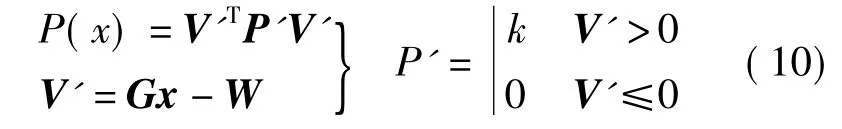
式中，k值根據經驗取一正整數值。應用不等式對坐標轉換過程中引起的長度變形進行約束的基本方法為：

1)首先應用一定的數學轉換模型(式(1))進行坐標系統轉換。

2)按國家相關測量規范的要求對控制點間的距離實測。

3)將控制點坐標與實測距離代入式(4)，如果滿足條件，則應用其控制成果。

4)如果不滿足條件，則使用式(9)重新進行平差計算。其中，罰函數的形式可通過式(10)確定，權值P'則根據控制點間的距離確定，進行迭代計算，直到都滿足式(4)為止。

三、算例分析

結合應用式(1)實現GPS控制測量成果坐標系統轉換的某線路工程控制點平面坐標，應用測距精度為±(2 mm+2×10－6×D)的TOPCON330全站儀對控制點間的距離進行實測，控制測量結果與實測距離、反算距離列于表1(部分數據選自文獻［13］)，長度變形值 λ1列于表2。其中，λ1表明測距邊2—3、3—4、4—5的長度變形值超出測量規范的要求，值大于1/40 000。因為1—2的長度變形值小于1/40 000，因此應用不等式對長度變形進行約束平差，結合式(9)與不等式約束實現的方法，只對控制點3、4、5坐標進行重新平差(1、2點坐標保持不變)，并進行迭代計算，控制點坐標與長度變形值λ2列于表2。λ2表明經不等式約束平差，測距邊2—3、3—4、4—5的長度變形值符合測量規范的要求，值小于1/40 000。

四、結束語

本文根據不等式約束的基本思想，給出能夠顧及長度變形的坐標系統轉換模型與轉換方法，給出對長度變形量約束的不等式具體形式，并對具體的轉換步驟進行探討。結合實測數據，對轉換方法進行驗證，結果表明這一方法能夠在坐標系統轉換過程中減小長度變形，使測量成果符合國家測量規范的要求。

表1 控制點坐標與點間距離 m

表2 不等式約束平差結果

［1］中華人民共和國交通部.JTJ/T 066—98公路全球定位系統(GPS)測量規范［S］.北京：人民交通出版社，1998.

［2］覃輝.某城市獨立坐標系與1954北京坐標系轉換方案［J］.測繪學院學報，2002，19(4)：247-250，254.

［3］馮亞明.利用GPS建立地方獨立坐標系［J］.武漢城市建設學院學報，1996，13(4)：17-20.

［4］施一民，李健.地方獨立坐標系的性質與區域性橢球的確定［J］.測繪通報，2001(9)：4-5.

［5］JUDGE G G，TAKAYAMA T.Inequality Restrictions in Regression Analysis［J］.Journal of the American Statistical Association，1966，61(313)：166-181.

［6］SCHAFFRIN B.Ausgleichung mit Bedingungs-ungleichungen ［J］.AVN，1981(6)：227-238.

［7］KOCH K R，RIESMEIER K.Bayesian Inference for the Derivation of Less Sensitive Hypothesis Tests［J］.Journal of Geodesy，1985，59(2)：167-179.

［8］REMONDI B W.Real-time Centimeter-accuracy GPS：Initializing While in Motion(Warm Start Versus Cold Start)［J］.Navigation，1993，40(2)：199-208.

［9］馮光財，朱建軍，陳正陽，等.基于有效約束的附不等式約束平差的一種新算法［J］.測繪學報，2007，36(2)：119-123.

［10］宋迎春，左廷英，朱建軍.帶有線性不等式約束平差模型的算法研究［J］.測繪學報，2008，37(4)：433-437.

［11］朱建軍，謝建.附不等式約束平差的一種簡單迭代算法［J］.測繪學報，2011，40(2)：209-212.

［12］姚宜斌.平面坐標系統相互轉換的一種簡便算法［J］.測繪與信息工程，2001(1)：1-3，18.

［13］林晏.大型線路工程獨立坐標系的建立方法研究［D］.阜新：遼寧工程技術大學，2010.