廣義高斯分布參數估值與樣本容量關系
董陽武,葛永慧
(1.山西煤炭職業技術學院地測系,山西太原030031;2.太原理工大學礦業工程學院,山西太原030024)
一、引 言
在廣義高斯分布(GGD)總體參數估計中,首要問題是選取多大規模的樣本。樣本容量太小,會使估計不夠精確;樣本容量太大,又會造成估算效率低下及人力物力的浪費。文獻[1-3]對參數估計時分別選取樣本容量 N=2000、N=4096和 N=65 536,這些樣本容量的選取是否科學合理,廣義高斯分布參數估計精度與樣本容量的關系如何,目前尚未見對此問題的論述。
本文從廣義高斯分布參數估計精度要求出發,采用矩估計法估算其參數,通過仿真試驗得到了廣義高斯分布形狀參數和尺度參數估計精度與樣本容量的定量關系,并給出了參數估計中樣本容量的確定方法,其在實際參數估算時極具實用性。
二、參數估計
廣義高斯分布概率密度函數(probability density function,PDF)可表示為[4-5]
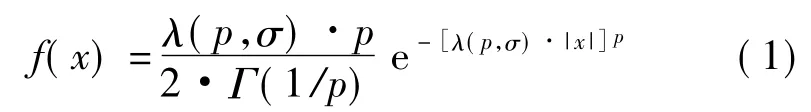
1.形狀參數估計
形狀參數估計方法有多種[6],但最常用的方法是極大似然法和矩估計法。極大似然法估計計算復雜,計算量大[7];而矩估計法被認為是實踐中最高效快速實用的方法。因此,本文選用矩估計法對形狀參數估計問題討論。
由矩估計法可得[1]
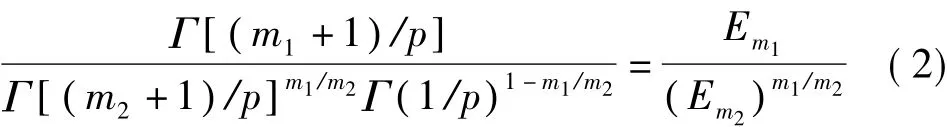
理論上,式(2)通過迭代計算可解出參數p,且m1、m2取值與被估參數p大約相等時矩估計結果收斂于極大似然估計結果,估計精度高、效果好[1]。本文基于此理論估算參數p,使結果具有最優收斂性,但其參數估計精度與樣本容量關系如何,在實際估算中,應如何選取樣本容量方可達到所需要的估算精度和估計效果,本文將通過仿真試驗對這些問題討論。
2.尺度參數估計
要得到樣本概率密度函數,除了要確定形狀參數外,還需要計算尺度參數(標準差)。樣本標準差計算公式為

式中,{x1,x2,…,xN}為來自均值 μ=0的 GGD 總體X樣本。
三、形狀參數估值與樣本容量關系
仿真試驗要得到形狀參數估計精度與樣本容量之間的關系,首先使樣本容量N取不同值(N≤60 000),對于每一個樣本容量N、形狀參數p和標準差σ,樣本發生器產生GGD樣本,用式(2)對參數p估算M=1000次,計算這M=1000個估算值的標準差和相對誤差。標準差和相對誤差計算公式分別為
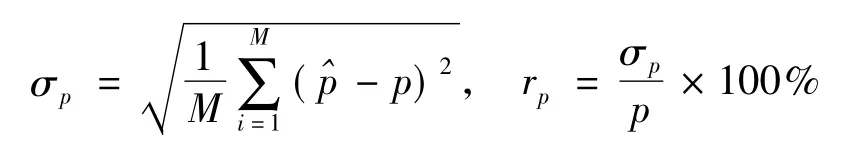
這樣在仿真試驗中就可得到每一個樣本容量N能達到的形狀參數估計精度rp。在仿真試驗中形狀參數 p 取0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0、5.5、6.0、6.5、7.0、7.5、8.0 等不同數值,當估計精度rp達到10%、5%、2.5%以下時可得到表1中形狀參數估計精度與樣本容量的定量關系,關系圖如圖1~圖3所示。
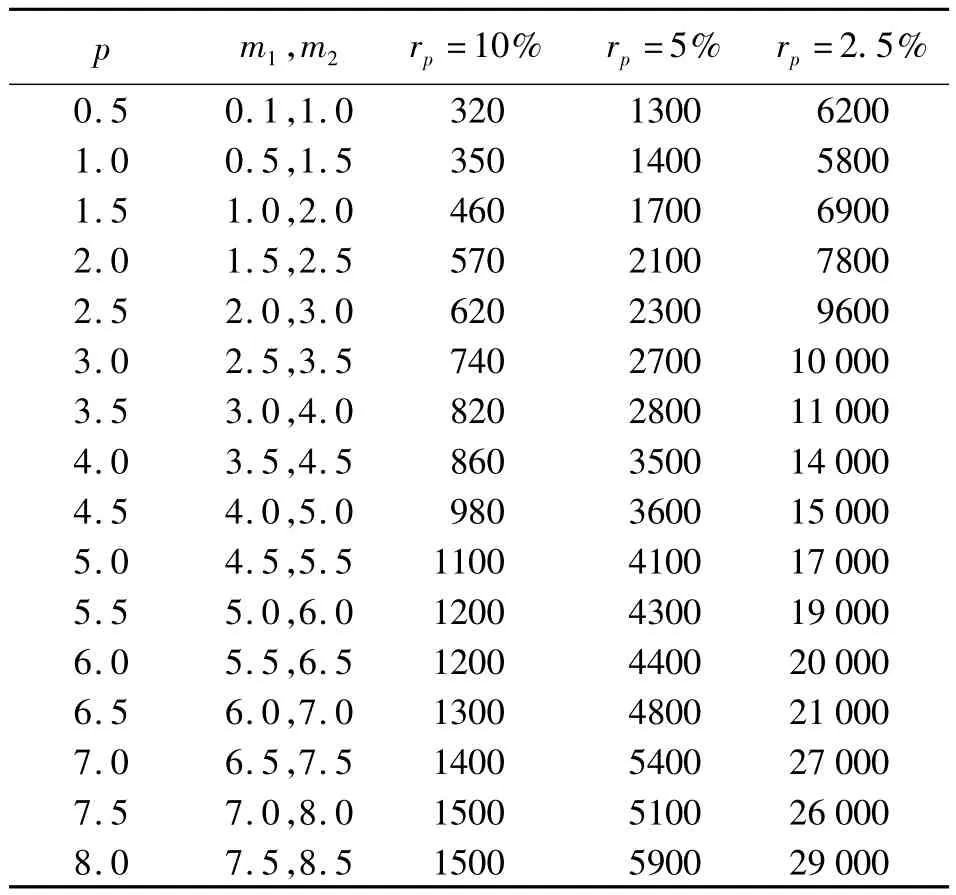
表1 形狀參數估值與樣本容量關系
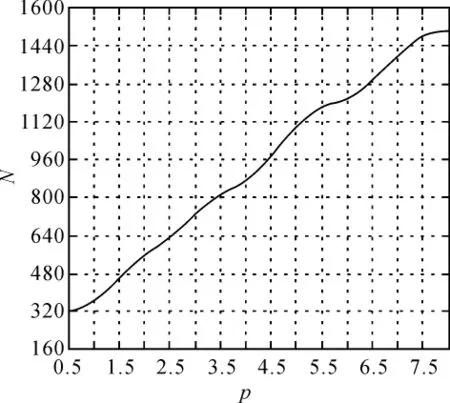
圖1 形狀參數估值與樣本容量關系(rp=10%)
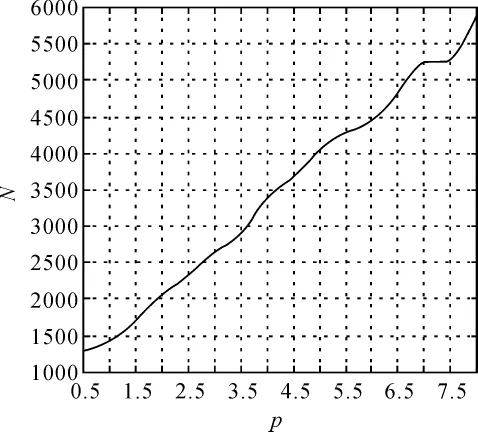
圖2 形狀參數估值與樣本容量關系(rp=5%)
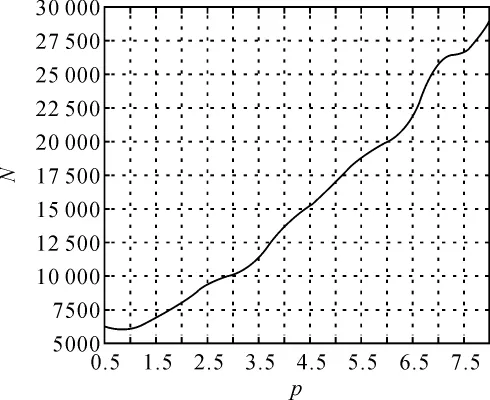
圖3 形狀參數估值與樣本容量關系(rp=2.5%)
四、尺度參數估值與樣本容量關系
仿真試驗要得到尺度參數估計精度與樣本容量之間的關系,首先使樣本容量N取不同值(N≤60 000)。對于每一個樣本容量N,樣本發生器產生GGD樣本,用式(3)對標準差σ估算M1=1000次,得到這M1=1000個估算值的平均值、標準差和相對誤差,這樣的估算過程重復M2=10次,則可得到每次算得的相對誤差平均值。樣本標準差平均值、標準差、相對誤差和相對誤差平均值計算公式分別為
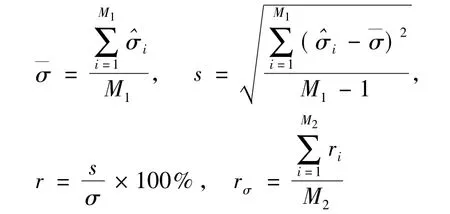
這樣在仿真試驗中就可得到每一個樣本容量N能達到的尺度參數估計精度rσ。仿真試驗中形狀參數 p 取0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0、5.5、6.0、6.5、7.0、7.5、8.0 等不同數值,尺度參數 σ 取 1.0,當估計精度 rσ達到10%、5%、2.5%以下時可得到表2中尺度參數估計精度與樣本容量的定量關系,關系圖如圖4~圖6所示。
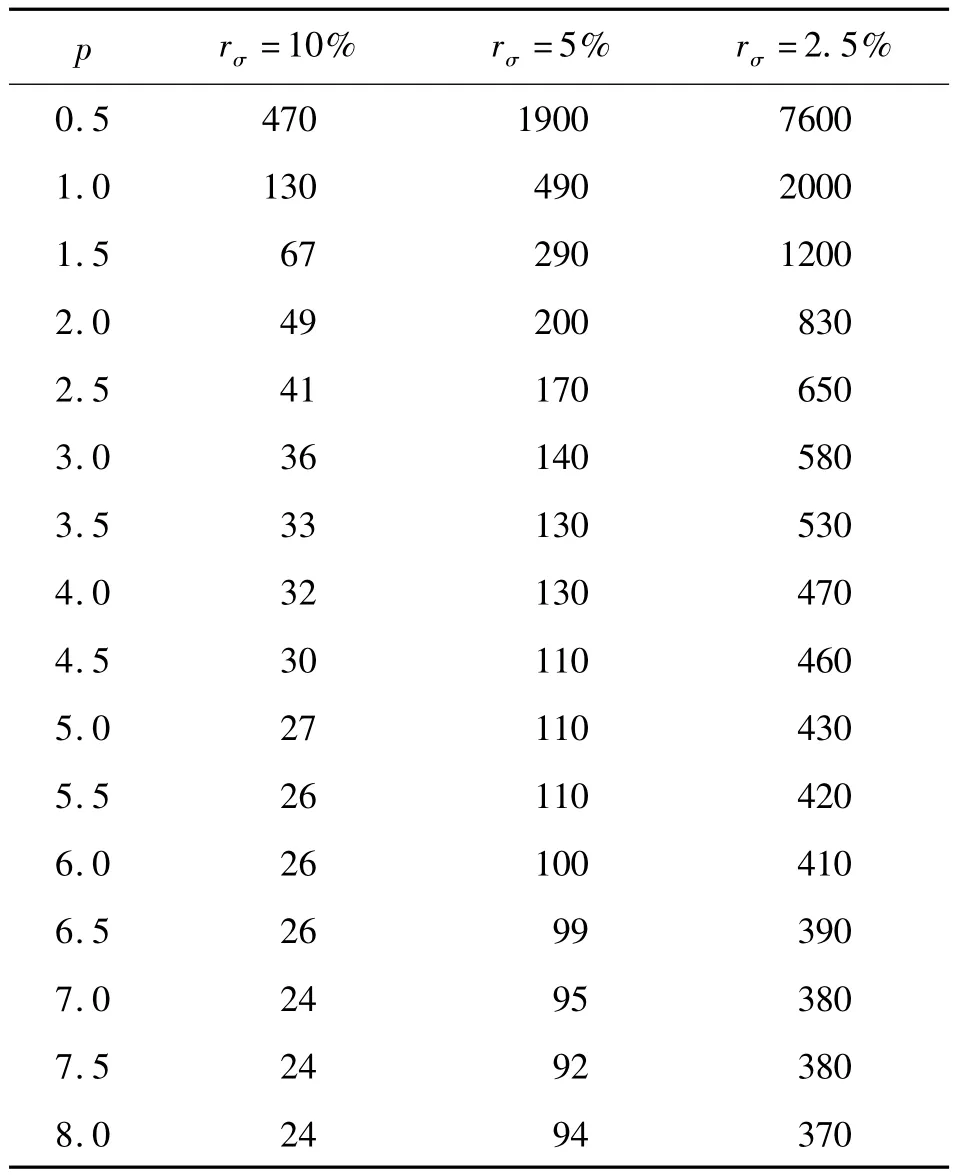
表2 尺度參數估值與樣本容量關系表
五、結論與建議
從圖1~圖3可得到10%、5%、2.5%精度約束下每個形狀參數估計精度與樣本容量的定量關系。矩估計法對形狀參數的估計最具代表性和典型性,因此對形狀參數估算所有方法的定量關系具有普遍參考價值,這樣在形狀參數估計選取樣本容量時就建立了一個參考標準,應參考圖1~圖3中的定量關系選擇合理的樣本容量,否則樣本容量太大會造成估算效率低下、資源浪費等缺點,樣本容量太小會使估算精度過低。
從圖4~圖6得到形狀參數取不同值時尺度參數估計精度與樣本容量間的定量關系。這樣在尺度參數估計選取樣本容量時也建立了一個參考標準,從圖4~圖6知,當p取不同值時σ估計收斂性不同,p越大,收斂性越好,因此σ估計收斂性與p有關,建議用式(3)估算σ時首先確定p,根據p值參考圖4~圖6判斷估計收斂性,選擇合理的樣本容量估算σ,否則盲目選取樣本容量會造成計算效率低、精度差、資源浪費。
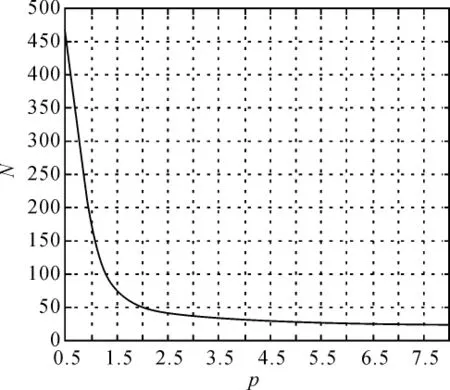
圖4 尺度參數估值與樣本容量關系(rσ=10%)
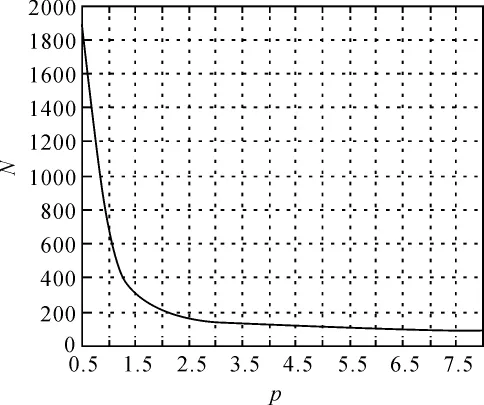
圖5 尺度參數估值與樣本容量關系(rσ=5%)
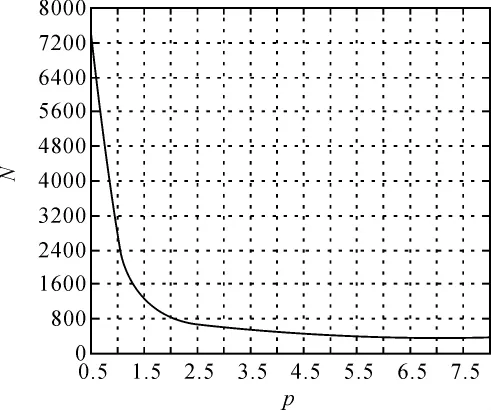
圖6 尺度參數估值與樣本容量關系(rσ=2.5%)
[1]KRUPIN'SKI R,PURCZYN'SKI J.Approximated Fast Estimator for the Shape Parameter of Generalized Gaussian Distribution[J].Signal Processing,2006,86(2):205-211.
[2]KRUPIN'SKI R,PURCZYN'SKI J.Modeling the Distribution of DCT Coefficients for JPEG Reconstruction[J].Signal Processing:Image Communication,2007,22(5):439-447.
[3]PI M.Improve Maximum Likelihood Estimation for Subband GGD Parameters[J].Pattern Recognition Letters,2006(27):1710-1713.
[4]DERRODE S,MERCIER G.Unsupervised Multiscale Oil Slick Segmentation from SAR Images Using a Vector HMC Model[J].Pattern Recognition,2007(40):1135-1147.
[5]CAI J,CHEN CW.Joint Source-channel Coding of GGD Sources with Allpass Filtering Source Reshaping[J].Journal of Visual Communication and Image Representation,2005,16(1):19-37.
[6]KOKKINAKISK,NANDI A K.Exponent Parameter Estimation for Generalized Gaussian Probability Density Functions with Application to Speech Modeling[J].Signal Processing,2005,85(9):1852-1858.
[7]AIAZZI B,BARONTI S,SANTURRI L,et al.Information-theoretic Assessment of Multi-dimensional Signals[J].Signal Processing,2005,85(5):903-916.

