Prediction Chatter Stability and Bifurcation in Milling Machine

ZHAO Demin, ZHANG Qichang

1.Department of Engineering Mechanics, College of Storage & Transportation and Architectural Engineering,China University of Petroleum, Qingdao 266555,China;2.Department of Mechanics，College of Mechanical Engineering, Tianjin University, Tianjin 300072,China

PredictionChatterStabilityandBifurcationinMillingMachine

ZHAO Demin1*, ZHANG Qichang2

1.DepartmentofEngineeringMechanics,CollegeofStorage&TransportationandArchitecturalEngineering,ChinaUniversityofPetroleum,Qingdao266555,China;2.DepartmentofMechanics，CollegeofMechanicalEngineering,TianjinUniversity,Tianjin300072,China

TheshiftedChebyshevpolynomialsandFloquettheoryareadoptedforthepredictionchatterstabilityandbifurcationinmilling.Thestabilitylobesdiagramisobtained.Thestabilityinmillingcanwellbepredictedbythelobesdiagram.Themuliti-periodicandHopfbifurcationsaredetectedbytheEigen-valuesanalysis.Theresultsshowedthatthestabilitysolutionofthesystemtransformfromthestableequilibriumpointtothelimitcycleoscillatoryaftermultiplecyclebifurcation,andittransformstothequasi-periodicoscillationafterHopfbifurcation.ThenumericalresultsofthePoincarésectionprovethattheoccurrenceofthequasi-periodicoscillation.

milling,chatterstability,Chebyshevpolynomials,bifurcation

1.Introduction

High-speed milling is in aerospace, ship, and many other industries due to its advantages such as high material remove rates, better surface finish and low cost. However, the chatter vibration of the machine tool-workpiece system is not only one of the main limitations for poor workpiece surface quality but also promotes wear of the machine tools. The basic and comprehensive mechanism of the machine chatter was presented by Tobias[1] and Altintas[2].

Because the cutting force is time-varying, it can be approximated by the zero-order or one-order Fourier series. Based on this principle, the analytical stability prediction method in frequency domain was introduced for the stability lobes in milling by Altintas[2-3]. Altintas[4] and Tang[5] summarized analytical stability prediction method in frequency domain and semi-discretization method in time domain for the two- or multi-degree-of-freedom (MDOF) system modal. The stability analysis on an uncertain dynamics milling model was performed and probabilistic instead of deterministic stability lobes were obtained in Reference[6]. Faassen[7] and Quintana [8] presented an experimental method to identify stability lobes diagram in milling operation. Gradisek[9] revealed periodic and quasi-periodic chatter by using the semi-discretization method. The quasi-periodic solutions of the time-periodic delay differential equations in high speed milling system were also identified by some milling experiments[10].

The time-varying periodic cutting force approximated by the zero-order or one-order Fourier series is not accurate for high-speed milling. Chebyshev polynomial[11-14] is an efficient computational scheme for the analysis of the periodic system. Therefore, this paper presented a stability theory which predicts chatter stability and bifurcation based on Chebyshev polynomial rather than Fourier series.

2.Dynamics model of milling

The cross sectional figure of the 2-degree-of-freedom(2-DOF) high-speed milling tool-workpiece system is shown in Fig. 1. The tool with the diameterD1and teeth numberzrotates at an angular speedΩ(rad/s). The radial immersion angle of the ith tooth varies with time as:φi(t)=Ωt+2π(i-1)/z.apandadescribes the axial and radial depth of immersion, respectively. The dynamics model of this machine tool-workpiece system is given by

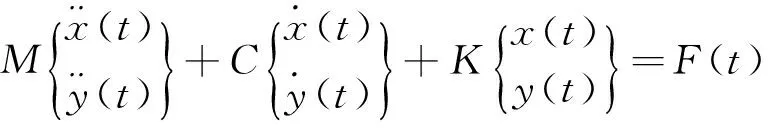
(1)

Where,M,CandKare the mode mass, damping and stiffness matrix, respectively,F(t) is the cutting force.

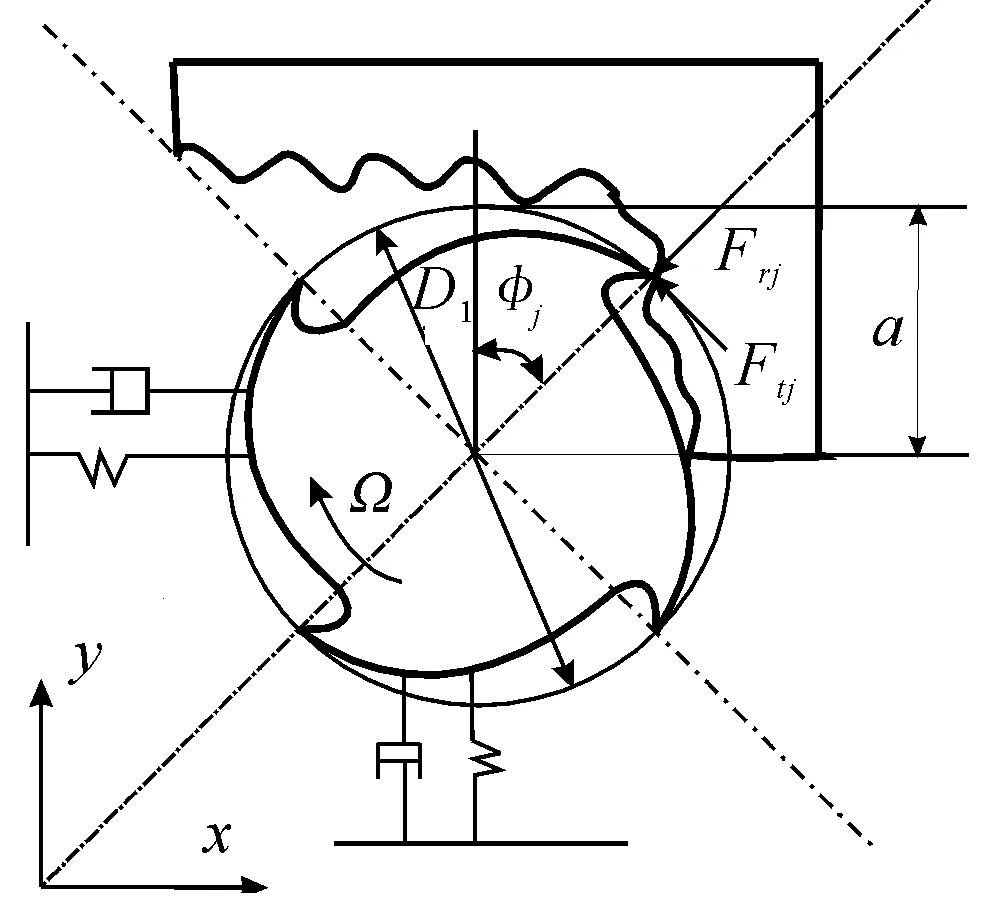
Fig.1 General sketch of the milling dynamic model with 2-DOF

2.1.Cuttingforcesmodel

The machine tool chatter vibrations occur due to a self excitation mechanism in generation of chip thickness during machining operations. An oscillatory surface finish left by one of the tooth is removed by the succeeding oscillatory tooth due to the structural vibrations. According to Altintas[4], the resulted chip thickness becomes also oscillatory, which could be expressed by

hj(t)=(Δx(t)sinφj(t)+

Δy(t)cosφj(t))g(φj(t))

(2)

where Δx(t)=x(t)-x(t-T),Δy(t)=y(t)-y(t-T),g(φj) describes a unit step function determining whether or not thejthtooth is in cutting.

(3)

Where,φstandφexare the start and exit angles of the cutter to and from the cutting, respectively.

The tangentialFtjand radialFrjcutting forces acting on the toothjare proportional to the axial depth of cutapand chip thicknesshj(t),

Ftj=ktaphj(t),Frj=krFtj

(4)

Where, the cutting coefficientsktandkrare constant. Resolve the cutting forces in thexandydirection

Fxj=-Ftjcosφj-Frjsinφj

Fyj=Ftjsinφj-Frjcosφj

(5)

The total cutting forces on the cutters contributed by all the teeth are given by

(6)

Rearranging Eq. (6) in matrix form yields

(7)

where:

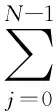
2.2.Governingstructuredynamicsmodel

Substituting Eq.(7) into Eq.(1) yields the following coupled delayed different equations with periodic coefficient:

(8)

In order to normalize the delay period toT=τ=1, we apply the following transformation:

(9)

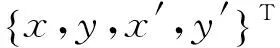
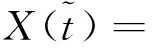
(10)

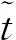
3.Shifted Chebyshev polynomials analysis

The shift Chebyshev polynomials can be generated by noting the following equations:

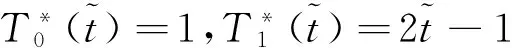
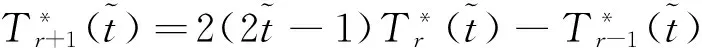
(11)

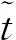
(12)

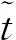
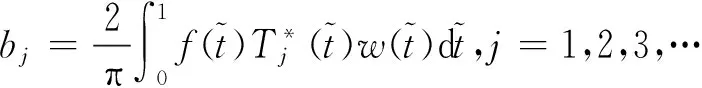
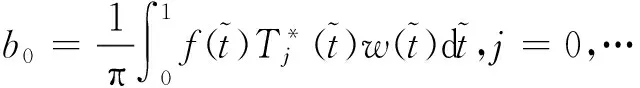
(13)

(14)

Where,I4is 4-order identity and ? denotes as Kronecker product. Based on the theory of the ordinary differential equation, the solution of the Eq. (10) is given by

C(s)X(s-1))ds

(15)

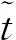
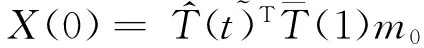
(16)

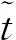
(17)

Substitute Eqs. (16 ) and (17) into Eq.(15), it yields:

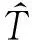
(18)

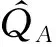
(19)

By simplify Eq. (19), we obtain:

(20)

Similarly, in the interval [i-1,i], the ith Chevbyshev coefficient vector relates to the counterpart of the previous interval as

(21)

Wcan be defined as an approximately monodromy operator

(22)

Based on the Floquet theory, the Eigen-values of monodromy operatorWcan predict the asymptotic stability of system. The cycle solution of the non-smooth dynamical system is stable if all the Eigen-values lie within the unit circle. The multiple cycle bifurcation occurs if one Eigen-value go through unit circle at point -1 and the saddle-note bifurcation occurs if the one Eigen-value go through unit circle at point +1. The Hopf bifurcation will take place if one pair Eigen-values go through unit circle at complex number.

4.Simulation and discuss

The system parameters are chosen according to Altintas[4]. Throughout of the paper, the value of the parameters are chose as:kt=900 (N/mm2),kr=0.3,ωnx=510 Hz,ωny=802 Hz,ζx=0.04,ζy=0.05,kx=96.2×10-6N/m,ky=47.5×10-6N/m,z=4. The cutter applied has four flutes with zero helix and the cutting condition is half immersion down milling. The 12-order shift Chebyshev polynomial is used in the simulation.

4.1.Chatterstabilityanalysis

Fig.2 gives the lobes diagram about spindle speedΩversus axial depth of cutap. The curve of the lobes demonstrates that the system with the parameters in the region of below the curve is stable as shown in Fig.3 and contrast to that the system is unstable if the parameters are in the region of above the curve. If the system parameters are on the curve, the system is in critical stability.

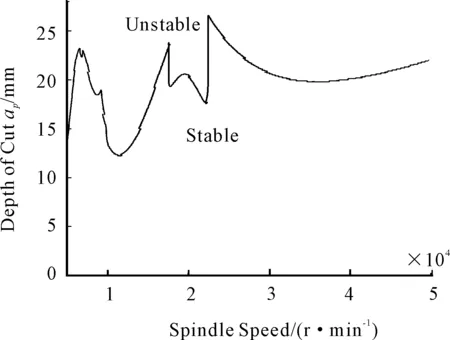
Fig.2 Stability lobes

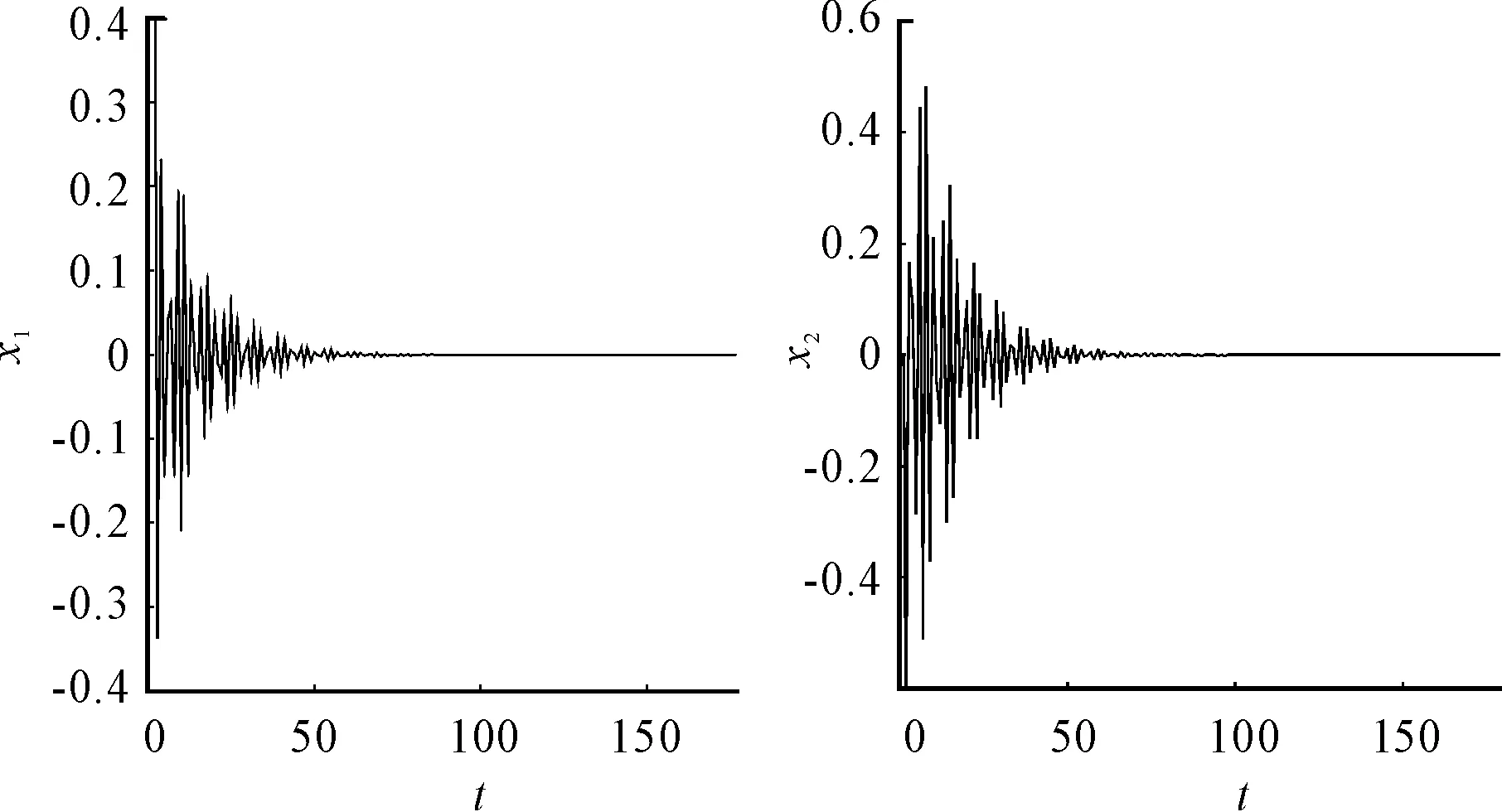
Fig.3 The time history plots of x 1 and x 2, when Ω=2.0×104 (r/min), a p=18 mm

4.2.Chatterbifurcationanalysis

The bifurcation analysis is only discussed when the milling system changes from stability to critical stability. When the parameters of the system are chosen on the critical stability curve，the real and imaginary part of one pairs of the Eigen-values of monodromy operatorW, whose modules is max among all Eigen-values, varies as the spindle speedΩas shown in Fig.4. The results indicate that when the spindle speed is in the region approximately 1.755×104≤Ω≤2.238×104, the multiple cycle bifurcation takes place. When the spindle speed is in the region 0.5×104≤Ω<1.755×104or 2.238×104<Ω≤5×104, the Hopf bifurcation takes place. No Eigen-values go through unit circle at +1, thus the saddle-note bifurcation never occurs.

Fig.5 and Fig.6 give the phase plane plots ofxandydirection whenΩ=2.0×104(r/min),ap=20.2 mm andΩ=3.5×104(r/min),ap=19.8 mm. Fig.5 demonstrates that the system converge to limit cycle oscillation (LCO) after multiple cycle bifurcation. The quasi-periodic oscillation occurs after Hopf bifurcation as shown in Fig.6.

Fig.4 The real and imaginary parts of the Eigen-values versus spindle speed

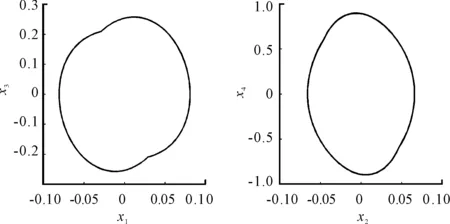
Fig.5 The phase plane plots of x and y directions, with Ω=2.0×104(r/min), a p=20.2 mm

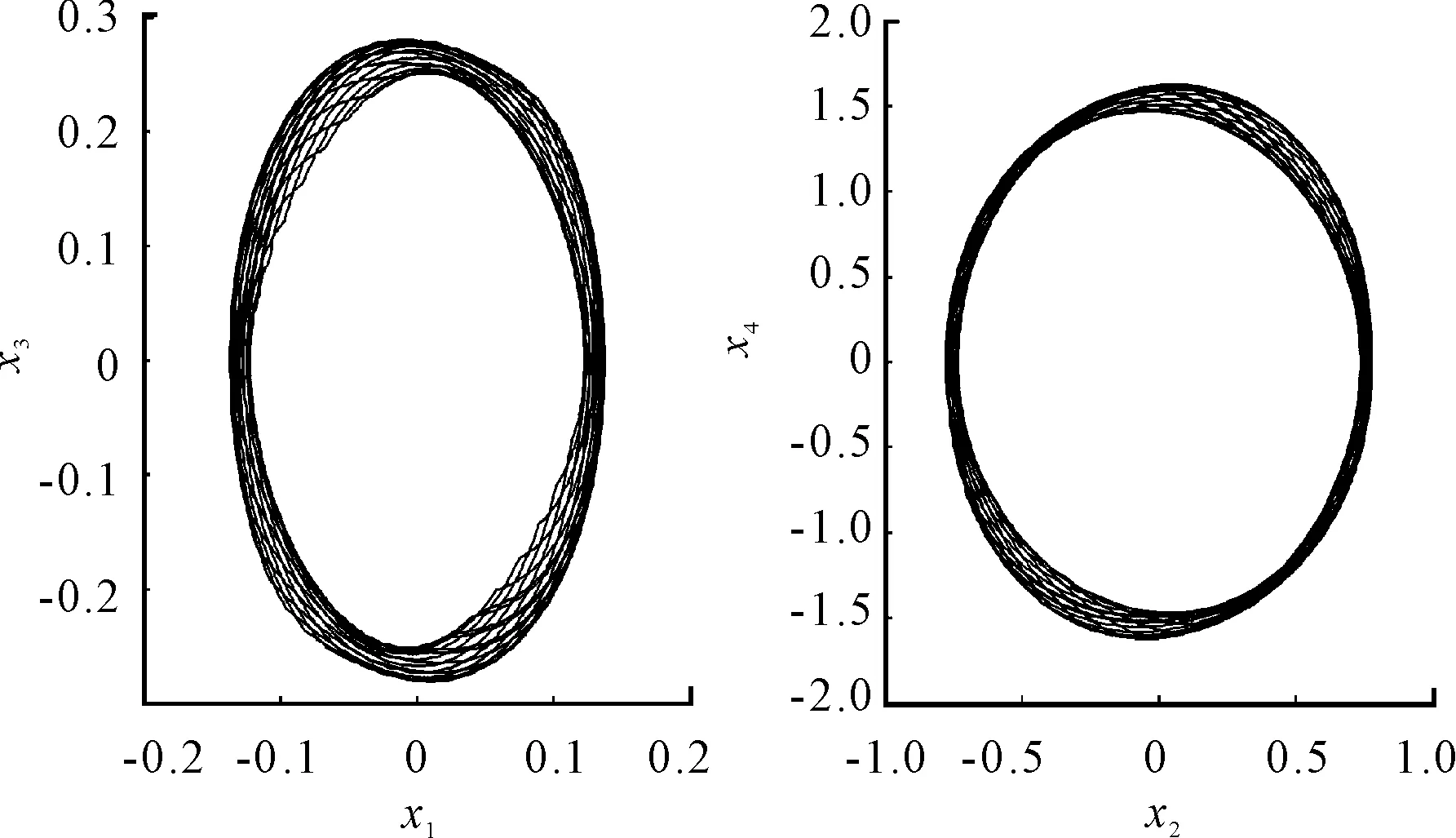
Fig.6 The phase plane plots of x and y directions with Ω=3.5×104(r/min), a p=19.8 mm

The Poincaré section figures as shown in Fig.7 (a),(b) and Fig.7 (c),(d) are obtained by performing 1.5×104and 21×104iterative times, respectively. WhenΩ=3.5×104(r/min),ap=19.8 mm, the Poincaré sections ofxandydirections are approximately ellipse, which also confirm occurrences of the quasi-periodic motions. Frequency components ration of the response, demonstrated in Fig.7 (a),(b), is approximately 1∶3.

Fig.7 The Poincaré section of in x and y directions which are obtained by performing different iterative times, when Ω=3.5×104(r/min), a p=19.8 mm, (a),(b):1.5×104 times; (c),(d): 21×104 times

5.Conclusions

The paper investigated the machine tool-workpiece system chatter vibrations in high speed milling. The shift Chebyshev polynomial and Floquet theory are efficiently adopted for this type of time-varying periodic delayed system. The stability and bifurcation are analyzed in the paper and the primary results of the present investigation can be summarized as follows:

The stability lobes have been obtained, which can give stability information about tool spindle speed and axial depth of cutting. Chatter bifurcation is analyzed by the Eigen-values of monodromy operator and the results confirm the multiple cycle bifurcation and Hopf bifurcation have onset in the milling system. After multiple cycle bifurcation, the stability solution of the system transforms from the stable equilibrium point to the LCO. After Hopf bifurcation, the stability solution transforms to the quasi-periodic oscillation. The Poincaré sections obtained also prove the occurrence of the quasi-periodic oscillation and give the frequency components ration of the response. Our achievement in this paper can provide important information for design of the 5-axial milling machine. This method is could be used to study the time-periodic delay-differential dynamics system.

[1] Tobias S A.Machine Tool Vibration[M].[S.l.]:Blackie and Sons Ltd,1965.

[2] Altintas Y, Budak E.Analytical Prediction of Stability Lobes in Milling[J].Annals of the CIRP,1995,44(1):357-362.

[3] Altintas Y.Analytical Prediction of Three Dimensional Chatter Stabolity in Milling[J].Japan Society of Mechanical Engineers International, 2001,44:717-723.

[4] Altintas Y,Stepan G,Merdol D.Chatter Stability of Milling in Frequency and Discrete Time Domain[J].CIRP Journal of Manufacturing Science and Technology,2008(1):35-44.

[5] TANG W X,SONG Q H,YU SQ, et al.Prediction of Chatter Stability in High-speed Finishing End Milling Considering Multi-mode Dynamics[J].Journal of Material Processing Technology, 2009,209:2585-2591.

[6] Totis G.RCPM-A New Method for Robust Chatter Prediction in Milling[J].International Journal of Machine tools & Manufacture,2009,49:273-284.

[7] Faassen R P H,Van de Wouw N,Oosterling J A J,et al.Prediction of Regenerative Chatter by Modelling and Analysis of High-speed Milling[J].International Journal of Machine tools & Manufacture,2003,43:1437-1446.

[8] Quintana G,Ciurana J,Teixidor D.A New Experimential Methodology for Identification of Stability Lobes Diagram in Milling Operations[J].International Journal of Machine tools & Manufacture,2008,48:1637-1645.

[9] Gradisek J,Kalveram M,Insperger T,et al.On Stability Prediction for Milling[J].International Journal of Machine tools & Manufacture,2005,45:769-781.

[10] Insperger T,Stépán G,Bayly P V,et al.Multiple Chatter Frequencies in Milling Processes[J].Journal of Sound and Vibration,2003,262:333-345.

[11] Butcher E A,Ma H T,Bueler E,et al.Stability of Linear Time-Periodic Delay-Fifferential Equations via Chebyshev Polynomials[J].International Journal for Numerical Methods in Engineering,2004,59:895-922.

[12] Sinha S C,Wu D H.An Efficient Computational Scheme for the Analysis of Periodic Systems[J].Journal of Sound and Vibration,1991,151:91-117.

[13] Butcher E A,Sinha S C.A Hybrid Formulation for the Analysis Time Preiodic Linear systems via Chebyshev Polynomials[J].Journal of Sound and Vibration,1996,195(3):518-527.

[14] Sinha S C,Butcher E A.Symbolic computation of fundmental solution Matrices for Linear Time-Periodic Dynamical Systems[J].Journal of Sound and Vibration,1997,26(1):61-85.

AppendixA

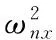
AppendixB

高速銑削顫振系統穩定性及分岔的Chebyshev多項式數值分析

趙德敏1*,張琪昌2

1.中國石油大學(華東) 儲運與建筑工程學院 工程力學系，山東 青島 266580；2.天津大學 機械工程學院 力學系，天津 300072

采用Chebyshev多項式法和Floquet理論相結合來預測銑床運行中的顫振和分岔。得到了穩定性極限形圖，可以準確地預示機床的穩定性。通過系統的特征值分析得到此系統發生了倍周期分岔和Hopf分岔。系統由穩定的平衡點通過倍周期分岔收斂到穩定的極限環運動，由Hopf分岔轉化到概周期運動。龐加萊截面的數值結果也證實了概周期運動的發生。

銑削；顫振穩定性；Chebyshev多項式法；分岔

TH17

2012-12-09

Project supported by the Fundamental Research Funds for the Central Universities (11CX04049A)， National Natural Science Foundation of China (10872141)*ZHAO Demin，Doctor.E-mail: zhaodemin@upc.edu.cn

10.3969/j.issn.1001-3881.2013.06.004