基于分形維數和小波域特征的計算機生成圖像檢測算法

孫 利,齊嘉銳,李巖波,萬國富

(1.吉林廣播電視大學,長春 130022； 2.吉林大學 軟件學院， 長春 130012；3.吉林大學 數學學院， 長春 130012； 4.吉林大學 計算機科學與技術學院,長春 130012)

自然圖像是指利用數碼相機拍攝得到的且未進行過任何篡改操作的照片圖像.計算機生成圖像是指利用計算機生成軟件繪制生成的圖像.自然圖像沒有經過任何篡改操作,是原始場景的真實寫照,是真實圖像.計算機生成圖像是人們利用各種計算機技術而獲得的圖像,違背真實場景,因此計算機生成圖像是假的圖像.例如圖1所示的自然圖像與計算機生成圖像,根據肉眼無法識別其真偽,因此只能從圖像的內部特征提取而進行區分.

隨著計算機技術的不斷發展,數字圖像篡改技術不斷進步,人們可以使用計算機軟件繪制出逼真的場景圖像,以致憑感官無法識別其真偽,使圖像的真實性面臨巨大挑戰.針對上述問題,目前已有許多檢測算法,例如: Ianeva等[1]利用空間域特征(如亮度、 飽和度和HSV顏色直方圖等)提取圖像特征檢測卡通圖片,但該算法不能有效用于檢測3D軟件生成的JPEG圖片;Lyu等[2]通過對圖像進行小波變換分解,提取其一階和高階小波系數作為統計量對兩種圖像進行區分,對自然圖像的檢測率達到67%,但該算法沒有從原理上指出計算機生成圖像和自然圖像的本質區別;姚丹紅等[3]利用分形維數進行計算機生成圖像檢測,但該算法檢測效果并不理想;Farid[4]利用小波域空間分析小波系數及其預測誤差的高階統計量,采用FLD線性分類器對自然圖像和計算機生成圖像進行訓練,但實驗效果也不理想;陳香蘋等[5]利用空間域和變換域的特征作為統計量進行計算機生成圖像的檢測,相比于Farid等的方法已經有了一些改進,但實驗效果依然不理想.除上述方法外,還有一些基于統計量的其他方法[6-7].

本文提出一種利用分形維數和小波域特征相結合的方法對自然圖像和計算機生成圖像進行檢測：將所有待檢測圖像分為訓練和測試兩部分.首先對樣本圖像進行分形維數特征和小波域特征的提取;然后將分形維數的特征和小波域特征組合,作為整個算法的高維分類特征,形成一個高階的特征向量;再用SVM分類器訓練樣本;最后使用SVM分類器對測試圖像進行測試.算法流程如圖2所示.實驗結果表明,本文算法檢測自然圖像和計算機生成圖像的效果較理想.

圖2 算法流程Fig.2 Framework of the algorithm

1 分形維數特征提取

1.1 圖像塊篩選

文獻[8]的檢測方法中沒有進行圖像塊篩選,直接對所有的圖像塊求取分形維數,因此檢測效果并不理想.本文采用先進行圖像塊篩選得到感興趣的圖像塊,然后進行分形維數特征提取的方法.

圖像塊篩選流程如下：

1) 將要輸入的圖像灰度化；

2) 將灰度化的圖像分成大小為K×K的若干圖像塊(如K=128)；

3) 計算各圖像塊的方差；

4) 確定篩選圖像塊的閾值,該閾值主要由實驗數據和相關經驗確定,本文篩選圖像塊閾值設置為1 000；

5) 將圖像塊方差與閾值進行比較,如果該圖像塊的方差大于閾值,則認為該圖像塊是感興趣圖像塊,保留該感興趣圖像塊并用于分形維數計算;如果該圖像塊的方差小于閾值,則認為該圖像塊像素變化平緩,丟棄該圖像塊.

按照上述方法,可得到需要進行分形維數特征提取的所有感興趣圖像塊.

1.2 分形維數計算

分形是一種具有自相似特性的現象、 圖像或物理過程,即局部特性和整體特性是相似的.用“維數”表示某個現象、 圖像或物理過程的不規則性和復雜性.

分形維數計算方法很多,本文采用“盒子”維算法[9],其算法流程如下：

1) 將得到的感興趣圖像塊(大小為K×K)考慮成一個三維空間,坐標(x,y)表示二維坐標平面,用于標記像素位置,圖像的灰度值表示Z軸方向;

2) 將二維平面(x,y)分成大小為l×l的若干格子(l為整數,且1≤l≤K/2),并令r=1/K;

3) 在每個格子中有許多體積為l×l×l的小盒子堆砌,使第(i,j)個格子中灰度表面的最大值和最小值分別落入堆砌序號(自下而上)為p和q的盒子中;

4) 令

nr(i,j)=p-q+1,

(1)

對所有的格子nr(i,j)求和,得

(2)

5) 用最小二乘法擬合lgNr-lg(1/r),求出的斜率即為盒子維數(dimension).

在“盒子”維算法中所有的立方體都放在固定的位置上,會出現立方體包裹不緊的情況,而對于l較大時,包裹不緊湊的情況更嚴重,會嚴重影響盒子的測量精度.因此本文算法將盒子數的計算方法修改為

nr(i,j)=(maxIk-minIk+1)/l.

(3)

該方法在盒子的計算過程中不再使用固定立方體的大小(l×l×l),而使用可變高度的長方體l×l×l′作為包裹曲面的盒子,這種方法對立方體的包裹更緊密,提高了分形維數的準確性.

2 小波域特征提取

本文針對由計算機3D軟件生成的JPEG圖像及由相機拍攝的JPEG圖像進行檢測,自然圖像成像過程中所產生的噪聲能在小波域上顯示,所以在小波域上能區分計算機生成圖像和自然圖像.本文采用如下小波變換四鏡像濾波器方法[4,7]:

1) 將輸入圖像灰度化；

2) 對該灰度圖像進行n級小波分解,各級小波分解后的水平子帶、 垂直子帶和對角子帶分別表示為Hi(x,y),Vi(x,y)和Di(x,y),其中i=1,2,…,n,表示第i級小波變換;

3) 對每個子帶系數計算其高階統計量,如均值、 方差、 偏度和峰度,得到一組特征,共12(n-1)維;

4) 利用線性誤差預測器分別對水平子帶、 垂直子帶及對角子帶的誤差計算其高階統計量,如均值、 方差、 偏度和峰度,得到第二組特征.

以垂直子帶為例,一個線性預測器表示如下:

其中ωk為加權因子.這種線性關系可用如下矩陣形式表示：

V=Qω,

(5)

其中: 列向量ω=(ω1,ω2,…,ω7)T;向量V包含垂直子帶小波系數的列向量;矩陣Q的每列由式(4)中相應的相鄰系數組成.其二次誤差函數定義如下：

E(ω)=(V-Qω)2,

(6)

該誤差函數通過對ω求導數并令導數值為零使E(ω)達到最小值,因此可求出

ω=(QTQ)-1QTV,

(7)

則線性預測器的對數誤差為

E=log2V-log2(Qω).

(8)

對E計算其均值、 方差、 偏度和峰度,該過程對于每級小波變換的垂直子帶都重復一次,則每級小波變換的線性預測器也要重新估計一次.對于水平子帶和對角子帶,計算過程相似.水平子帶的線性預測器形式如下：

對角子帶的線性預測器形式如下：

線性誤差預測器得到的均值、 方差、 偏度和峰度的特征維數為12(n-1),再結合小波子帶系數統計量,則小波域特征共24(n-1)維,從而形成了一個特征向量,并可區分自然圖像和計算機生成圖像.

3 分類器的選擇

由于分形維數和小波域特征相互組合而得到的高維特征通常是線性不可分的,SVM解決線性不可分問題效果較好,因此本文選擇支持向量機(SVM)[10-12]作為算法的分類器.SVM的核心思想是對最優分類面的推廣,即最大化不同類別間的分類間隔.SVM通常采用內積函數定義的非線性變換將輸入空間轉換到高維,使原來低維空間中線性不可分的問題變成高維線性可分,然后在高維空間中求解廣義最優分類面問題.

假設xi(i=1,2,…,N)為特征向量,則分類器的目的是設計超平面g(x)=ωTx+ω0=0.其中:ω是超平面系數向量;x是輸入向量;ω0是偏移量.與兩類樣本點距離最大的分類超平面會獲得最佳的推廣能力,即滿足下式的最優分類超平面：

其中yi為+1和-1分別表示待分類的兩類樣本.假設λ1,λ2,…,λN是N個Lagrange乘子,K(xi,x)為映射核函數,則由式(11),(12)可得最終判別函數為

(13)

典型的核函數有線性核、 多項式核及RBF核等.在本文算法中,采用RBF核函數的C-SVC,即

K(xi,x)=exp(-γ‖xi-x‖2),

(14)

其中參數C和γ通過網格搜索獲得最佳參數,搜索范圍均為{2-5,2-4,…,25}.

4 實驗結果

本文實驗選擇800張JPEG圖片作為原始圖片集,其中400張是自然圖像,來源于哥倫比亞大學數字圖像庫,另外400張計算機生成圖片主要來自3D圖片網站.選擇200張自然圖像和200張計算機生成圖像作為訓練樣本,另外的200張自然圖像和200張計算機生成圖像作為測試樣本.實驗步驟如下：

1) 讀取一幅輸入圖像,同時得到其所屬類別(Photorealastic Image=1,Computer Generated Image=-1);

2) 提取圖像的分形維數特征;

3) 提取圖像的小波域特征,對輸入圖像進行4層小波分解,可得到小波域共72維特征;

4) 重復1)～3),完成所有輸入圖像的特征提取;

5) 利用Libsvm中的easy.py進行交叉驗證,尋找訓練模式時的最優參數;

6) 利用步驟4)得到的圖像特征與步驟5)得到的最優參數建立SVM模型;

7) 利用步驟6)得到的SVM模型對測試圖像進行檢測.

圖3為實驗檢測階段400張測試圖片的檢測結果,橫坐標為400張測試圖片的序號,縱坐標表示預測值,縱坐標為“1”表示自然圖像,縱坐標為“-1”表示計算機生成圖像,“●”表示實際值,“■”表示預測值.由圖3可見,“●”與“■”的重疊部分表示預測正確的圖片,孤立的“■”表示預測錯誤的圖片.

圖3 400張圖片檢測結果Fig.3 Detected results of 400 images

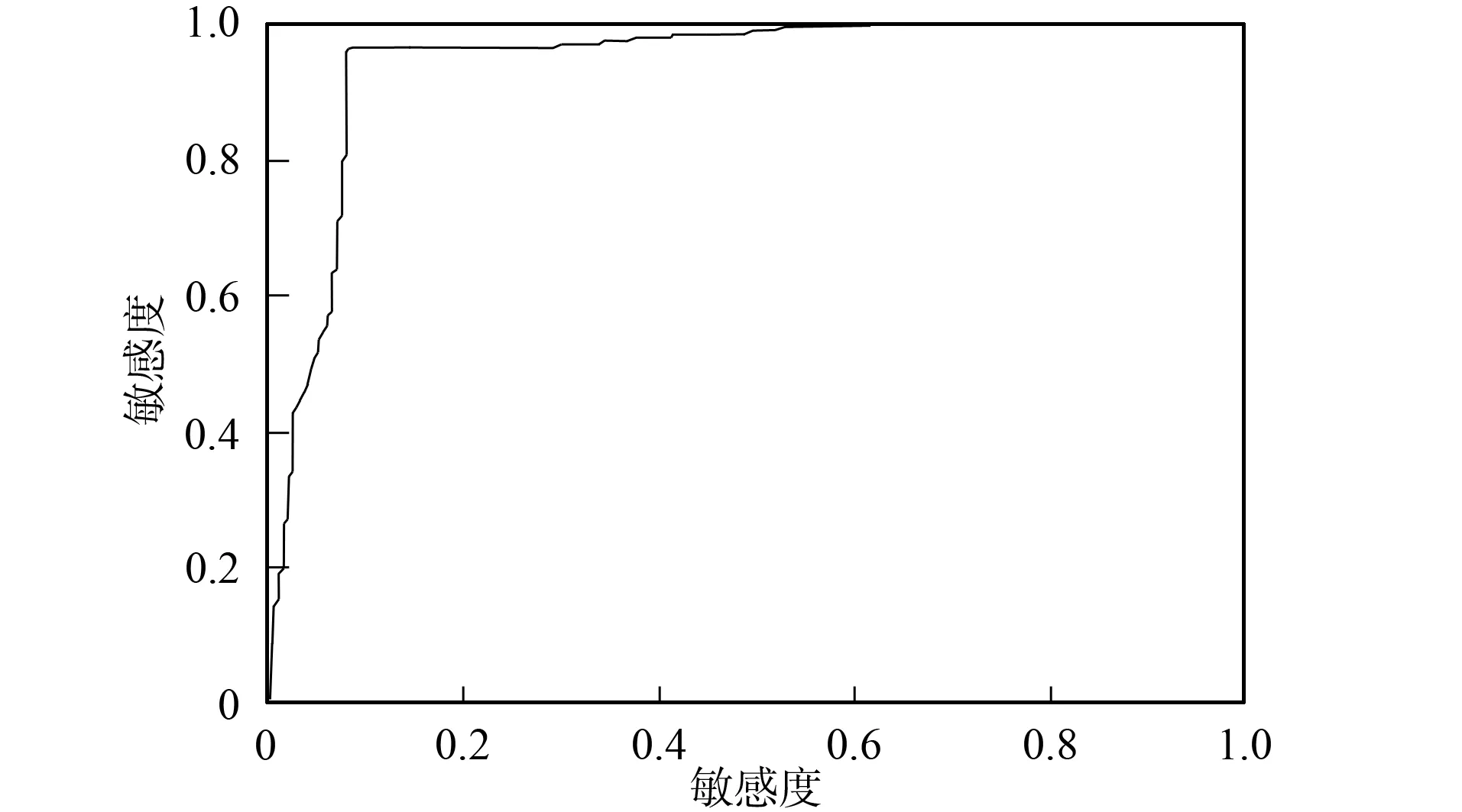
圖4 ROC曲線Fig.4 ROC curve

圖4為衡量上述400張圖片預測結果的ROC(receive operating characteristic)曲線,ROC曲線下方面積用AUC表示,AUC越大,表示預測結果越精確,預測的理想結果是AUC=1.由圖4可見,本文實驗的AUC=0.943 0,是一個理想的數值.

表1列出了本文算法與文獻[7]中檢測準確率的對比結果,其中總檢測準確率由自然圖像檢測準確率和計算機生成圖像檢測準確率的算術平均得到.由表1可見,本文算法對自然圖像和計算機生成圖像的檢測準確率有較大提高.

表1 自然圖像和計算機生成圖像的檢測準確率Table 1 Identifying accuracy of photographic and computer generated images

綜上所述,本文提出了一種多特征結合的自然圖像和計算機生成圖像檢測算法,先將分形維數特征和小波域提取的高階統計量作為圖像的統計特征,再利用SVM分類器對自然圖像和計算機生成圖像進行分類和檢測.實驗結果表明,本文算法對自然圖像和計算機生成圖像的檢測準確率有很大提高.

[1] Ianeva T I,Vries A P,De,Rohrig H.Detecting Cartoons: A Case Study in Automatic Video-Genre Classification [C]//IEEE International Conference on Multimedia and Expo.Piscataway: IEEE Press,2003: 449-452.

[2] Lyu S,Farid H.How Realistic Is Photorealistic [J].IEEE Trans Signal Processing,2005,53(2): 845-850.

[3] YAO Dan-hong,SU Bo,LI Sheng-hong.Fractal-Dimension Based Algorithm to Detect Computer Graphics [J].Communications Technology,2008,41(12): 256-258.(姚丹紅,蘇波,李生紅.基于分形維數的計算機生成圖像檢測方法 [J].通信技術,2008,41(12): 256-258.)

[4] Farid H.Detecting Hidden Messages Using Higher-Order Statistics Models [C]∥International Conference on Image Processing.Piscataway: IEEE Press,2002: 905-908.

[5] CHEN Xiang-ping,LI Sheng-hong,SU Bo,et al.Identifying Computer Generated Images Based on Analysis of Image Noise [J].Journal of Optoelectronics·Laser,2010,21(2): 293-297.(陳香蘋,李生紅,蘇波,等.基于圖像噪聲分析的計算機生成圖像檢測算法 [J].光電子·激光,2010,21(2): 293-297.)

[6] ZHANG Zhen,REN Yuan,PING Xi-jian.Distinguishing Computer Graphics from Nature Image on Interpolation Algorithms [J].Journal of Geomatics Science and Technology,2009,26(4): 288-291.(張震,任遠,平西建.基于插值算法的真實圖像與計算機生成圖像鑒別 [J].測繪科學技術學報,2009,26(4): 288-291.)

[7] WANG Yu-ping,LI Sheng-hong,ZHAO Feng,et al.Detection of Photorealistic Computer Graphic Based on AdaBoost [J].Computer Simulation,2008,25(7): 220-222.(王玉平,李生紅,趙峰,等.基于AdaBoost的計算機生成圖像檢測算法 [J].計算機仿真,2008,25(7): 220-222.)

[8] Ng T T,Chang S F,Tsui M P.Physics-Motivated Features for Distinguishing Photographic Images and Computer Graphics [C]∥Proceedings of the 13th Annual ACM International Conference on Multimedia.New York: ACM,2005: 239-248.

[9] LIU Mei-hong,XU Wei-hong.Detection of Copy-Move Forgery Image Based on Fractal and Statistics [J].Journal of Computer Applications,2011,31(8): 2236-2239.(劉美紅,徐蔚鴻.基于分形和統計的復制-粘貼篡改圖像的檢測 [J].計算機應用,2011,31(8): 2236-2239.)

[10] WANG Bo,KONG Xiang-wei,YOU Xin-gang,et al.Blind CFA Interpolation Detection Based on Covariance Matrix [J].Journal of Electronics &Information Technology,2009,31(5): 1175-1179.(王波,孔祥維,尤新剛,等.基于協方差矩陣的CFA插值盲檢測算法 [J].電子與信息學報,2009,31(5): 1175-1179.)

[11] WANG Bo,KONG Xiang-wei,YOU Xin-gang,et al.Identification of Source Cameras Based on CFA Interpolation Algorithm Detection Using Covariance Matrix [J].Journal of Optoelectronics·Laser,2009,20(4): 517-520.(王波,孔祥維,尤新剛,等.利用協方差矩陣檢測CFA插值的相機來源鑒別方法 [J].光電子·激光,2009,20(4): 517-520.)

[12] ZHANG Xue-gong.Introduction to Statistical Learning Theory and Support Vector Machines [J].Acta Automatica Sinica,2000,26(1): 32-42.(張學工.關于統計學習理論與支持向量機 [J].自動化學報,2000,26(1): 32-42.)