基于新型順序約束的產品可靠性評估方法研究＊

應新雅 張志華

（海軍工程大學理學院 武漢 430033）

1 引言

產品的研制通常要經歷設計樣機、樣機試驗、發現問題并對樣機進行改進、再試驗、最后產品設計定型等多個階段，在工程上通常將定型產品稱為正樣，將以前各階段的產品稱為樣機。在產品研制過程中，通常積累有大量可靠性研制試驗，并通過不斷暴露產品設計存在的問題及改進設計，使產品可靠性穩步提高。如何有效利用產品研制階段的可靠性研制信息，客觀評估產品正樣階段的可靠性，并在充分利用可靠性研制試驗信息基礎上，組織開展產品可靠性鑒定試驗，以減少產品可靠性鑒定試驗量，解決傳統可靠性鑒定試驗量大，實施困難的問題，一直是可靠性統計研究領域的重要問題。

對于可靠性增長試驗信息的處理問題，很多專家學者進行了大量研究工作，提出了多種可靠性增長試驗信息處理方法。如文獻［1］提出的AMSAA模型在假定產品故障為連續改進情況下，產品可靠性增長實際上是一個Weibull過程，并給出了產品失效率評估方法。在許多產品研制過程中，產品故障往往采用集中處理方式，此時，產品的可靠性增長呈現出階梯增長。文獻［1～3］針對階梯增長情況提出了順序約束Bayes評估方法，利用不同研制階段的失效率的順序約束條件對產品失效率進行評估。此外，文獻［4］還提出了加速因子Bayes評估方法，文獻［5］利用先驗均值和先驗分位數方法制定產品可靠性鑒定試驗方案，試圖充分利用產品可靠性研制試驗信息來減少產品可靠性鑒定試驗量。但是，上述文獻在處理階梯型可靠性增長試驗數據時均沒有考慮到產品各研制階段的失效率減小幅度。事實上，在產品設計改進過程中，隨著產品設計缺陷的不斷被暴露，盡管產品失效率呈現出減小趨勢，但其減小量卻是逐步遞減的。實際上，AMSAA模型在要求其增長參數小于1時描述了產品失效率減小量逐漸減小這一特征。因此，對于階梯型可靠性增長試驗信息的處理，不僅需要考慮產品失效率隨著研制階段的推進是順序減小的，而且還需要考慮產品失效率的減小幅度是逐步減小的，以便客觀評估產品正樣階段的可靠性。

本文在充分考慮產品在各個研制階段的失效率減小幅度順序減少的基礎上，提出了產品失效率新的順序約束條件，即產品失效率在相鄰階段的比值也應滿足順序減少約束。在此基礎上，給出了一種新的產品失效率順序約束Bayes評估方法，并基于上述評估方法研究了產品可靠性鑒定試驗方案制定方法。通過算例數據分析，與傳統的順序約束Bayes評估方法進行對比，發現本文給出的評估方法更能準確評估產品失效率，所給出的可靠性鑒定試驗量較傳統的方法要大，反映了利用失效率減小量的順序約束是必要的。

2 先驗分布的確定

為了客觀利用產品可靠性研制信息給出正樣產品的失效率估計，本節首先研究產品失效率的先驗信息，確定產品失效率的先驗分布。

假設產品的整個研制過程分為m個階段，其中前m－1個階段為產品的樣機試驗階段，第m個階段為產品的（正樣）定型階段，并設第i個階段產品壽命服從指數分布：

隨著試驗的不斷進行，產品的缺陷逐步暴露，繼而對產品進行改進，可靠性得到提高。此時產品的失效率滿足順序約束：

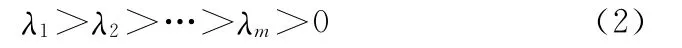
產品在試驗過程中，產品設計缺陷得到不斷暴露并被修正，其產品設計中的殘留缺陷對產品可靠性的影響也越來越小，反映到產品失效率的變化上就是，產品失效率不僅需要滿足傳統的順序約束條件（2），而且還應滿足以下順序約束：

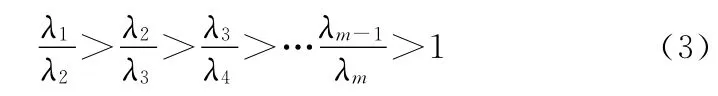
新的順序約束（3）實際上是要求在產品相鄰研制階段的失效率比值是順序減少的，這表明隨著產品設計改進，其可靠性增長幅度也越來越小。實際上，在常見的AMSAA模型中，當增長參數小于1時產品失效率隨著研制過程的推進降低幅度也越來越小，因此，在階梯型可靠性增長模型中，要求產品失效率滿足新的順序約束（3）是合理的。同時，新的順序約束實際上包括了傳統的順序約束（2）。事實上，由于λ2／λ3＞1，則

類似地，可以得到產品失效率在滿足新的順序約束（3）時，有λ1＞λ2＞…＞λm＞0。因此，順序約束條件（3）是評估產品失效率時應使用的先驗信息。

設產品失效率λi的無信息先驗分布為其共軛分布，即

由Box－Tiao方法［5］可知，其中超參數取值為Ti0＝0，zi0＝0，所以產品失效率λi的無信息先驗分布為

由于第m個階段為產品正樣階段，在短時間試驗情況下通常不會發生故障，因此，為能夠正常處理正樣階段的可靠性研制試驗信息，一般對正樣失效率的先驗分布中超參數取值較為保守，如由Box－Tiao方法［5］可知，λm的無信息先驗分布為

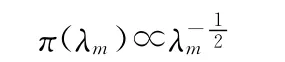
由λ1，λ2，λ3，…，λm的獨立性知，（λ1，λ2，λ3，…，λm）的無信息聯合先驗分布為

3 正樣失效率λm的Bayes估計

假定產品在m個階段的可靠性研制試驗信息為（Ti，zi）（i＝1，2，…，m），即在i個階段，進行了總試驗時間為Ti內，發生了zi次故障。這里試驗包括定數截尾試驗和定時截尾試驗，則其似然函數為

設各階段試驗是相互獨立的，則整個樣機階段的似然函數為

其中t＝｛（Ti，zi），i＝1，2，…，m－1｝。

在有了產品在m階段的可靠性研制試驗信息的似然函數的基礎上，利用（λ1，λ2，λ3，…，λm）的先驗分布，就可以得到（λ1，λ2，λ3，…，λm，t）的聯合密度函數為

聯合密度函數g（λ1，λ2，λ3，…，λm，t）包含了所有正樣失效率的信息，由Bayes定理得到定型產品失效率λm的后驗分布為

其中

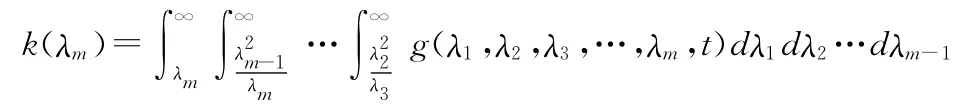
在平方損失下，正樣失效率λm的Bayes估計為

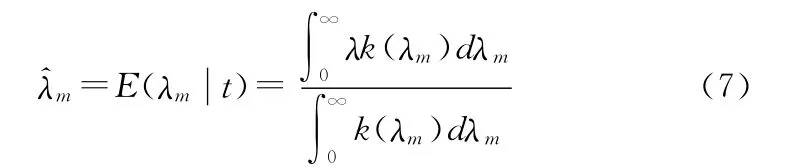
相應地，正樣失效率λm的二階矩估計為

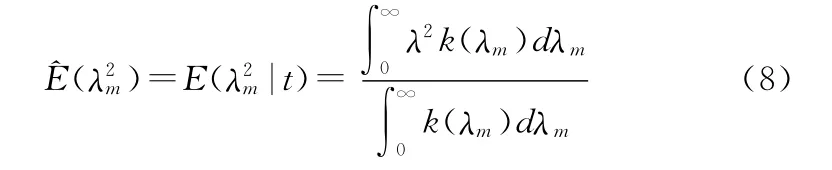
特殊地，當m＝3時，產品正樣失效率λ3的后驗分布可進行適當簡化。利用不完全Gamma函數與Poisson分布累積項之間的恒等式［1］：

則

因此，產品正樣失效率λ3的后驗分布可簡化為

4 產品失效率鑒定方案

隨著產品可靠性要求越來越高，利用經典統計方法開展可靠性鑒定試驗所需要的試驗量較大，從而造成可靠性鑒定試驗實施十分困難。因此，充分利用產品可靠性研制試驗信息，制定產品可靠性鑒定試驗方案，是減少鑒定試驗量的有效途徑。為此，本節將在產品正樣失效率評估結果基礎上，研究制定產品可靠性鑒定試驗方案的方法。

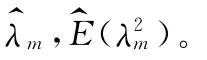
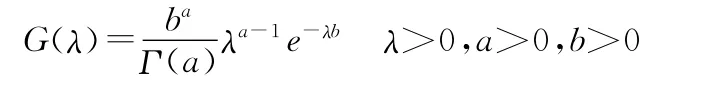
其中a與b為先驗分布的超參數。

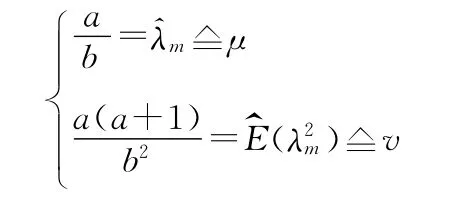
則

有了正樣產品失效率λm的先驗分布后，就可以制定產品可靠性鑒定方案［3］。假設產品可靠性鑒定方案為（c，Tc）（其中c表示最大允許失效數，Tc為總試驗時間），在進行可靠性鑒定試驗時，抽取n件產品，做有替換定時t0截尾試驗，記總試驗時間Tc＝nt0，試驗過程中失效產品數r服從Poisson分布：

由λm的先驗分布式（9）和似然函數式（10）可以得到λm的后驗分布：

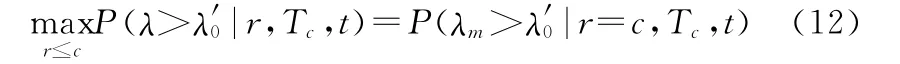
假設規定使用方的風險為β，則有：

等價于P（λm≤λ′0｜r＝c，Tc，t）≥1－β，即

當給定c時，通過上式求解出相應的總試驗時間，繼而得到鑒定試驗方案（c，Tc），當產品通過鑒定，則保證定型產品達到使用方要求的最小概率1－β，否則產品不能通過鑒定。

5 算例分析

為了說明本文提出的新順序約束Bayes評估方法是有效的，本節處理某產品在研制過程中所獲得的可靠性研制試驗信息。該產品研制過程分為原理樣機、初樣機和正樣機等三個階段，在原理樣機和初樣機階段分別獲得的可靠性研制試驗信息分別為（r1，t1）＝（2，300），（r2，t2）＝（1，1200），由于經過初樣機的改進，工程技術人員認為該產品正樣基本成熟，在該產品可靠性鑒定試驗前沒有組織專門的可靠性研制試驗，即在正樣階段沒有可靠性研制試驗信息。

假定該產品設計要求最低壽命為10000小時，即其極限失效率為λ′0＝1×10－4，規定使用方風險為β＝0.2，利用新的順序約束條件（9）得到先驗分布的超參數為a＝0.623，b＝1255.2。基于上述先驗信息，對于不同的合格判定數c，可得到相應的可靠性鑒定試驗時間記為Tc，具體試驗時間見表1第二行。為了對比該方案，在表1中列出了經典的可靠性鑒定試驗方案（表1第一行）和基于傳統的順序約束Bayes評估結果得到的可靠性鑒定試驗方案（表1第三行）。從三種鑒定試驗方案可以看出，利用本文方法所得到的鑒定試驗時間明顯低于經典的可靠性鑒定試驗時間，但比基于傳統的順序約束Bayes評估方法所得到的可靠性鑒定試驗時間要長，這也說明考慮本文所給出的產品失效率順序約束對產品可靠性鑒定試驗方案有明顯影響。從這個意義上來說，新的順序約束條件（3）是客觀評估正樣產品失效率所必須要考慮的。

表1 利用不同方法得到的鑒定試驗方案

6 結語

本文通過改進產品失效率的順序約束，給出了產品失效率的新的順序約束Bayes評估方法，并基于產品正樣失效率評估結果，研究了可靠性鑒定試驗的Bayes方案。通過實例分析表明，本文所給出的新的順序約束條件對客觀評估產品正樣失效率，能夠避免傳統的順序約束Bayes評估方法所得評估結果的冒進現象，對準確掌握產品可靠性增長規律具有重要意義。

［1］周源泉，翁朝曦.可靠性增長［M］.北京：科學出版社，1992：260－263，120－127.

［2］茆詩松，湯銀才，王玲玲.可靠性統計［M］.北京：高等教育出版社，2008：106－107.

［3］張志華.可靠性理論及工程應用［M］.北京：科學出版社，2012：260－263.

［4］張志華，姜禮平.指數型產品失效率鑒定試驗的Bayes方案［J］.應用概率統計，2000，16（1）：66－70.

［5］陳宜輝，姜禮平，吳樹和.指數分布下Bayes鑒定試驗方案［J］.運籌與管理，2002，11（2）：56－59.

［6］Box，G.E.，Tiao，G.C.Bayesian Inference in Statistical A－nalysis［M］.Addison－wesley Reading，1973.

［7］田艷梅，張志華.成敗型產品驗收試驗方案研究［J］.海軍工程大學學報，2003，15（5）：75－78.

［8］韓慶田，盧洪義，張毅.系統可靠性增長評估模型研究［J］.航空動力學報，2009（11）.

［9］周源泉.質量可靠性增長與評定方法［M］.北京：北京航空航天大學出版社，1997.

［10］梅文華.可靠性增長試驗［M］.北京：國防工業出版社，2003.

［11］張金槐，張士鋒.多層驗前信息下可靠性增長的Bayes分析［J］.質量與可靠性，2003（6）.

［12］吳啟光，李國英，趙勇輝.用于指數可靠性增長模型的一類新的先驗分布［J］.數學物理學報，2003（4）.