基于離散GM(1，1)模型的武器備件故障率預測研究

邵延君，馬春茂，潘宏俠，劉永姜

(1.中北大學,山西 太原 030051；2.西北機電工程研究所,陜西 咸陽 712099)

武器裝備由于生存的環境特殊性和設備本身的老化等因素的影響，會不可避免地出現故障,但由于武器裝備復雜程度不同，使其表現出的故障規律存在較大差別[1-3]，通過對大量故障數據進行統計分析后，可以得到故障率隨時間變化的典型的故障率曲線，典型的故障率λ(t)隨工作時間t的變化趨勢具有3個明顯的區域，人們形象地把它稱為“浴盆曲線”[4]。早期故障期的故障率呈逐漸下降的趨勢;偶然故障期的故障率接近于常數;耗損故障期的故障率呈逐漸上升趨勢。通過對典型的故障率曲線進行分析，發現早期故障期和耗損故障期的故障率λ(t)隨時間呈非線性變化，于是考慮用GM(1，1)模型對早期故障期和耗損故障期兩個階段的故障率進行預測，GM(1，1)模型對于非線性序列進行預測具有一定的優勢，但是傳統的GM(1，1)模型對非線性序列預測存在較大誤差，離散GM(1，1)模型則能夠比較精確模擬非線性序列，因此考慮用離散的GM(1，1)模型對武器備件的故障率進行預測[5-6]。

1 GM(1，1)建模

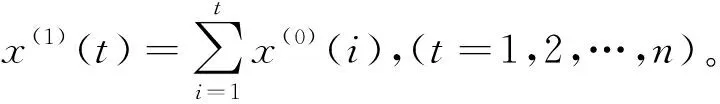
2)對生成的序列X(1)(t)有如下一階線性白化微分方程dx(1)/dt+ax(1)=b，當t取單位時間時，一階微分方程的差分形式等于微分形式，dx(1)/dt=x(1)(t+1)-x(1)(t)=x(0)(t)，所以GM(1，1)模型的微分方程可以表示為：x(0)(t) +ax(1)(t)=b，稱為GM(1，1)模型的原始形式。

3)為了使一次累加生成序列更平滑，對X(1)作緊鄰均值生成。Z(1)=(z(1)(2),z(1)(3),z(1)(4),…,z(1)(n))，其中z(1)(t)=0.5(x(1)(t)+x(1)(t-1))，x(0)(t)+aZ(1)(t)=b為GM(1，1)模型的基本形式。式中：a為發展系數；b為灰作用量；Z(1)為X(1)的緊鄰均值生成序列。

4)對GM(1，1)模型的基本形式的參數a、b進行求解。……