Banach 空間中關于公共不動點的強收斂性定理.

胡松林，姚小杰

(湖北師范學院 數(shù)學與統(tǒng)計學院, 湖北 黃石 435002)

在本章中, 令E為實Banach 空間,E*是E的對偶空間. 令C是的E中的非空閉凸子集.T:C→C是非擴張： ‖Tx-Ty‖≤ ‖x-y‖ , ?x,y∈C. 如果x∈C有Tx=x則x是T的不動點.定義F(T) = {x∈C:Tx=x}. 我們用J:E→ 2E*的正規(guī)對偶算子

Jx= {f*∈E*: = ‖x‖2= ‖f*‖2}

其中〈.,.〉 廣義對偶對. 容易知道如果E*嚴格凸則J是單值， 如果E是一致光滑則J在E的有界子集上一致連續(xù). 另外, 如果E自反嚴格凸的Banach 空間并且對偶空間也嚴格凸則J-1是單值, 一對一的, 滿射. 在Hilbert 空間H中,J就是恒等算子.

我們知道如果C是HilbertH上的非空閉子集和PC:H→C是投影算子, 則PC是非擴張的. 實際上這個經常用來刻畫Hilbert 空間, 但是并不能用在Banach 空間中. 所以, Alber[1]在Banach 空間E引進了一個更一般的投影算子∏C:

φ(x,y) = ‖x‖2- 2 〈x,Jy〉+ ‖y‖2

(1)

(‖x‖ -‖y‖)2≤φ(x,y) ≤ (‖x‖ + ‖y‖)2對任意x,y∈X

和

φ(x,y) ≤φ(x,z) +φ(z,y) + 2 〈x-z,Jz-Jy〉 對任意x,y∈X

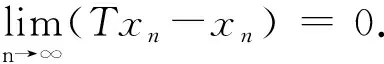
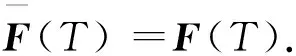
最近, Shin-Ya Matsushita, Kazuhide Nakajo 和Wataru Takahash[5～6]引進了下面一個迭代序列(2) 關于可數(shù)個閉的相對半非擴張映射，其中xn是按照下面的方式生成:

(2)

其中Tn, (n= 0, 1, … ,∞) 滿足(H) 條件.

(H): {an} ? (-1,∞) 和{bn} ?[0,∞) 使得

φ(z,Tnx) ≤φ(z,x) -anφ(x,Tnx) -bnφ(Tnx,x)

在本文中, 主要受上面定理的啟發(fā), 我們在Banach 空間中引進了迭代方式，并且強收斂于可數(shù)個閉相對半非擴張映射的公共不動點.

1 預備知識

在我們主要定理的證明過程中將用到下面的一些引理.

引理1[1]令K實光滑Banach 空間E中的閉凸子集，x∈E且x0∈K. 則φ(x0,x) =inf {φ(z,x):z∈K} 成立當且僅當

〈z-x0,Jx0-Jx〉 ≥ 0, ?z∈K

引理2[1]令K是實自反嚴格凸光滑的Banach 空間E 中的閉凸子集,x∈E. 則y∈K,

φ(y,Kx) +φ(Kx,x) ≤φ(y,x)

引理3[7]令E是實光滑嚴格凸的Banach 空間,xn和yn為E中兩個點列. 如果xn和yn有界且φ(xn,yn) → 0當n→ ∞, 則xn,yn→ 0, 當n→ ∞.

引理4[6]令E是一致凸的Banach 空間,BR(0) 是E中的閉球. 則存在一個連續(xù)的嚴格增的凸函數(shù)g: [0,∞) → [0,∞) ，g(0)=0 使得

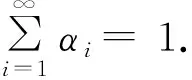
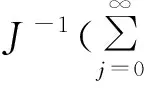
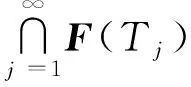
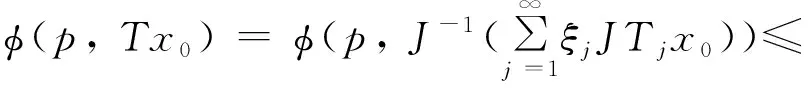
φ(p,x0)-λg(‖JTkx0-Jx0‖

因為JTkx0=Jx0,所以有Tkx0=x0.

2 主要結果

定理1 令C是一致凸一致光滑的實Banach 空間E中的非空閉凸子集.Ti:C→C,i∈是一族閉相對半非擴張映射且滿足

令xn由下面方式生成:

(1)

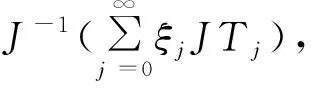
定理1 先證明Cn是閉凸的. 由Cn的定義知道是閉的. 我們證明Cn是凸的， 因為

φ(z,yn) ≤φ(z,xn) -anφ(xn,yn) -bnφ(yn,xn)

?2 〈z,Jxn-Jyn〉 + ‖yn‖2-‖xn‖2+anφ(xn,yn) +bnφ(yn,xn)≤0

所以Cn是凸的. 下面我們證明F?Cn. 利用歸納法. 顯然F?C=C0. 假設F?Ck則有

φ(p,yk-1) ≤φ(p,xk-1) -anφ(xk-1,yk-1) -bnφ(yk-1,xk-1)

因此p∈Ck+1.F?Cn所以(1) 有定義.

由xn=∏Cnx0和引理2 有

φ(xn,x0) =φ(∏Cnx0,x0) ≤φ(p,x0) -φ(p,xn) ≤φ(p,x0).

則φ(xn,x0) 有界. 另外xn=∏Cnx0，xn+1= ∏Cn+1x0∈Cn+1?Cn所以

φ(xn,x0) ≤φ(xn+1,x0), ?n≥ 1.

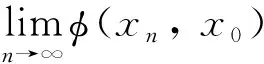
φ(xn+m,xn) =φ(xn+m,∏Cnx0)≤φ(xn+m,x0) -φ(∏Cnx0,x0)=

φ(xn+m,x0) -φ(xn,x0).

則φ(xn+m,xn) → 0 當n→ ∞. 由引理3 可得

xn+m-xn→ 0, 當n→ ∞

(2)

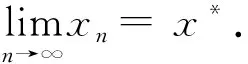
φ(xn+1,yn) ≤φ(xn+1,xn) -anφ(xn,yn)

(3)

有

φ(xn,yn)=‖xn‖2-2 〈xn,Jyn〉 + ‖yn‖2=

‖xn+1‖2- 2 〈xn+1,Jyn〉 + ‖yn‖2+ ‖xn‖2- ‖xn+1‖2+ 2 〈xn+1-xn,Jyn〉=

φ(xn+1,yn) + ‖xn‖2-‖xn+1‖2+ 2 〈xn+1-xn,Jyn〉

(4)

將(3),(4)相加得

(1 +an)φ(xn,yn)≤φ(xn+1,xn) + ‖xn‖2-‖xn+1‖2+ 2〈xn+1-xn,Jyn〉≤

φ(xn+1,xn) + (‖xn‖ + ‖xn+1‖ + 2 ‖yn‖) ‖xn+1-xn‖

(5)

因為{xn} 有界, 存在M> 0 使得

‖yn‖2≤M‖yn‖ +M

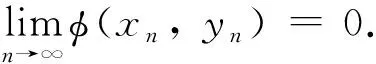
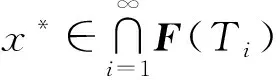
最后證明x*=∏Fx0. 由xn=∏Cnx0有

〈z-xn,Jx0-Jxn〉 ≥ 0, ?z∈Cn

因為F?Cn有

〈p-xn,Jx0-Jxn〉 ≥ 0, ?p∈F

(6)

對(6) 取極限有

〈z-x*,Jx0-Jx*〉 ≥ 0, ?p∈F

由引理1 有x*=∏Fx0. 完成定理證明.

參考文獻:

[1]Alber Ya I.Metric and generalized projection operators in Banach spaces: Properties and applications, In:A.G. Kartsatos (Ed).Theory and Applications of Nonlinear Operators of Accretive and Monotone Type[M]．Dekker:New York, 1996.

[2]Cioranescu I.Geometry of Banach spaces, Duality Mapping and Nonlinear Problems[M]. Amsterdam:Kluwer Academic publishers, 1990.

[3]Alber Ya I, Reich S.An iterative method for solving a class of nonlinear operator equations in Banach spaces, Panamer[J]. Math J,1994,4:39～54.

[4]Butanriu D, Reich S, ZasIavski A J.Weak convergence of orbits of nonlinear operators in reflexive Banach spaces[J].Numer Funct Anal Optim,2003,24: 489～508.

[5]Zegeye H, Ofoedu E U, Shahzad N.Convergence theorems for equilibrium problem, variational inequality problem and countably infinite relatively quasi-nonexpansive mappings[J].Nonlinear Anal Hybird Systems,2010,in press.

[6]Zegeye H.A hybrid iteration scheme for equilibrium problems, variational inequality problems and common fixed point problems in Banach spaces[J].Nonlinear Analysis,2010,72:2136～2146.

[7]Kamimura S, Takahashi W.Strong convergence of proximal-type algorithm in a Banach space[J].SIAM J Optim,2002,13:938～940.

[8]Peng J W,Yao J C.A new hybrid-extragradient method for generalized mixed equilibrium problems, fixed point problems and variational inequality problems[J].Taiwanese J Math,2008,12 :1401～1432.

[9]Yao Y,Liou Y C,Yao J C.New relaxed hybrid-extragradient method for fixed point problems, a general system of variational in equality problems and generalized mixed equilibrium problems[J].Optimization ,2010,(in press).

[10]Nadezhkina N, Takahashi W.Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings[J]. J Optim Theory Appl,2006,128 :191～201.

[11]Zeng L C, Yao J C.Strong convergence theorem by an extragradient method for fixed point problems and variational inequality problems[J].Taiwanese J Math 2006,10:1293～1303.

[12]Korpelevich G M.An extragradient method for finding saddle points and for other problems[J].Ekon Mate Metody,1976,12:747～756.

[13]Kohasaka F, Takahashi W.Strong convergence of an iterative sequence for maximal monotone operators in Banach spaces[J]. Abstr Appl Anal,2004,3:239～249.

[14]Qin X, Cho Y J, Kang S M.Convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces[J]. J Comput Appl Math,2008, doi:10.1016/j.cam.2008.06.011.