一類階段結構和B-D功能性反應的三種群順環捕食系統

晉金才，竇霽虹，楊建飛

（1.西安郵電大學 電子工程學院，陜西西安 710121；2.西北大學 數學系，陜西西安 710127；3.西北大學 經濟管理學院，陜西西安 710127）

在生物數學中，具有階段結構或者具有功能性反應的生物數學模型被研究者所重視[1-9]，文獻[1]研究了具有Beddington-DeAngelis功能性反應的三維順環捕食系統，得到了系統一致持續生存、存在唯一全局漸近穩定正周期解與概周期解的充分條件，文獻[2,10]研究了食餌具有階段結構和Beddington-DeAngelis功能性反應的兩種群食餌-捕食者模型的持久性和周期解的存在性。本文對一類同時具有階段結構和Beddington-DeAngelis功能性反應的非自治三種群順環捕食系統進行研究①。

1 數學模型

本文研究了一類具有階段結構和Beddington-DeAngelis功能性反應的非自治三種群順環捕食系統②，即

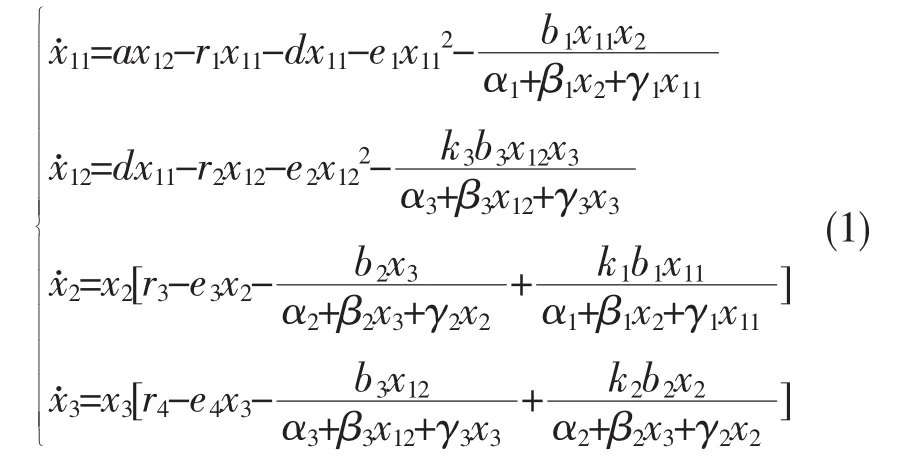
其中 x11(t)，x12(t)，x2(t)，x3(t)分別表示種群 1 的幼年個體和成年個體及種群2,種群3在t時刻的種群密度，幼年個體x11(t)不能捕食x3(t)，成年個體 x12(t)捕食 x2(t)，x2(t)捕食 x3(t)，x3(t)捕食幼年個體x11(t)，ri(t),i=1,2,3,4為種群的死亡率，a(t)為成年個體對新生幼年個體的轉化系數，d(t)為幼年個體向成年個體的轉化系數，ei(t),i=1,2,3,4為密度制約系數。這里所有系數都是關于t函數，比如a=a(t))，且都是定義在[0,+∞]上連續的正周期函數，并記

定義1[1]對于系統的任意正解(x11(t),x12(t)，x2(t),x3(t)),若存在實數M≥m＞0滿足

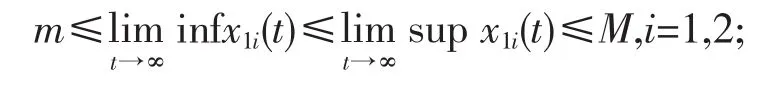
引理1[5]若微分不等式滿足y(t)(p-qy(t))，y(t)=x(0),其中 p，q 是常數，則其解滿足不等式

引理2[11](Brouwer不動點定理)假設中的有界閉凸集，T∈C(Ω,Ω)，則存在 X0∈Ω，使得TX0=X0。

引理3[12]設f（x）為定義在[0，+∞]上的非負可微函數，若有界，則為一常數，且有

2 定理及其證明

定理1如果系統(1)的解滿足初值條件xli(0)＞0，xj(0)＞0，i=1，2，j=2，3 那么系統(1)的所有滿足初值條件解最終都滿足xli（t）＞0，xj(t)＞0,i=1，2，j=2，3。……