框架梁梁端彎矩調幅計算方法研究

張艷如 李云貴 李守功

(1.建研科技股份有限公司，北京 100013;2.中國建筑科學研究院，北京 100013)

1 引言

鋼筋混凝土框架結構因其自身的材料性質，決定了以目前的計算手段，在日常設計計算分析時只能用線彈性方法，在結構達到承載能力極限狀態時計算與實際會有較大差異，主要表現在構件剛度的相對變化而引起內力重分布方面。因此在設計時應盡量考慮這種差異，能更合理地估計結構的承載能力和使用階段性能，充分發揮結構潛力，收到節約材性、簡化計算、方便施工的效果。目前常用的辦法是對梁的支座負彎矩進行彎矩調幅。

2 國內外現狀及規范規定

2.1 國外現狀及規范規定

國內外還有很多學者、院校及科研機構對調幅系數都進行了大量的試驗和理論研究，并且都給出了詳盡的調幅公式，給我們后來的學者鋪好了良好的進一步提高的階梯。

(1)美國規范

美國規范ACI318－05 允許對鋼筋混凝土構件進行的調幅值為1000εt，εt為最外層受拉鋼筋的應變，最大不超過20%。彎矩減小后的截面εt應大于或等于0.007 5。

如果容許的彎矩調幅值用配筋率ρ 表示，則

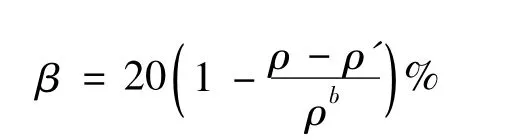
式中:ρ—受拉縱向配筋率;

ρ' —受壓縱向鋼筋配筋率;

ρb—平衡配筋率(平衡梁開裂彎矩的配筋率)。

用上式進行負彎矩調幅時，彎矩減小后截面的ρ 或ρ－ ρ' 應等于或小于0.5ρb。當ρ 或ρ－ ρ' 大于0.5ρb，不能進行調幅。

(2)歐洲規范

歐洲規范EN1992－1－1:2004 規定用δ 表示彎矩調幅系數，為調幅后的彎矩與彈性彎矩的比值，這與美國規范不同即:β=1－ δ。其規定，對主要承受彎矩的板，相鄰板跨的跨長比應為0.5～2.0。當滿足下列條件時，不需檢驗板塑性鉸的轉動能力而直接進行彎矩調幅:

式中δ—調幅后的彎矩與彈性彎矩之比;

xu—調幅后極限狀態時中和軸的高度;

d—截面有效高度;

k1～k6—系數，由執行歐洲規范國家的國家指定的附錄文件規定。如果設計中不能確認截面的轉動能力，歐洲規范規定不能按塑性重分布進行設計。

2.2 國內現狀及規范規定

1988 年，重慶筑大學、天津大學、清華大學進行《鋼筋混凝土連續梁和框架考慮內力重分布設計規程》［2］的編制工作。該設計規程地給出了各種荷載形式和各種支座約情況下的鋼筋混凝土連續梁、單向連續板和框架的彎矩調幅系數計算公式，全面和系統地研究了鋼筋混凝土連續梁和框架在考慮彎矩調幅進行結構設計時結構內力計算的原理，規程規定調整后的截面彎矩不小于按彈性方法計算所得彎矩的75%。

但是，前人的研究成果中大部分都是給出了彎矩調幅的一個范圍，即調幅系數在0.75～1.0 之間，各設計單位和設計人員也都是根據自己的工程經驗進行取值，并且一般認為梁剛度減小其端支座彎矩也會減小，相應調幅系數要變化，但是并沒有再進一步的深入研究梁剛度的變化與調幅之間是否存在某種聯系。所以對調幅系數的進一步的研究就存在著可行性和必要性。本文主要討論梁剛度與調幅的關系。

3 算例數值分析

本文通過采用SATWE 結構計算軟件，對不同結構形式的梁進行梁剛度變化對調幅的影響計算分析，其中所選模型有門式框架，三跨鋼架，三維框架。先通過改變整個梁剛度，觀察梁剛度變化對梁彎矩的影響。此時在梁剛度系數變化下所得梁彎矩設為Mk，本文梁剛度系數k 取0.5、0.7、0.85、1.0、1.15、1.3、1.5、1.7、2.0。M0指梁剛度系數為1.0 時的彎矩，此為一參考值。其后將梁分成7 段，梁跨中段剛度系數為b 取1.0、0.8、0.6 時，分別變化梁兩端支座處兩段的剛度系數，觀察梁剛度變化對其彎矩的影響。此時梁兩端支座處剛度系數變化下的彎矩設為Ma，其剛度系數a 的取值為1.0、0.8、0.6、0.4、0.2。同時以整個梁剛度系數取1.0時為其參考值。文中假設δ'=Mk/M0為整梁剛度系數變化所得彎矩變化系數，δb=Ma/M0為分段梁跨中梁段剛度系數b 取1.0、0.8、0.6，兩端支座處剛度系數a 變化所得彎矩變化系數。

3.1 門式框架

3.1.1 門式框架無分段梁

圖1 門式框架整梁模型圖

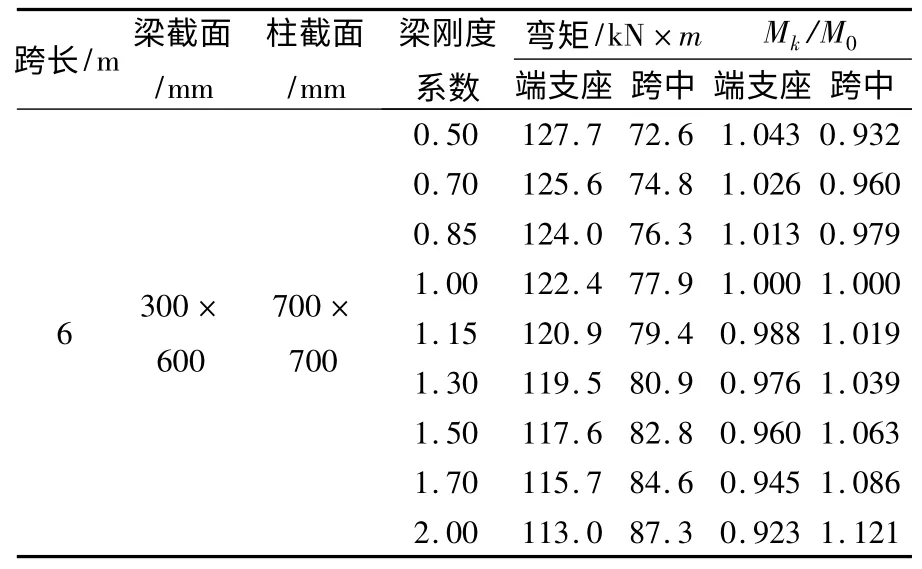
表1 門式框架整梁彎矩變化表

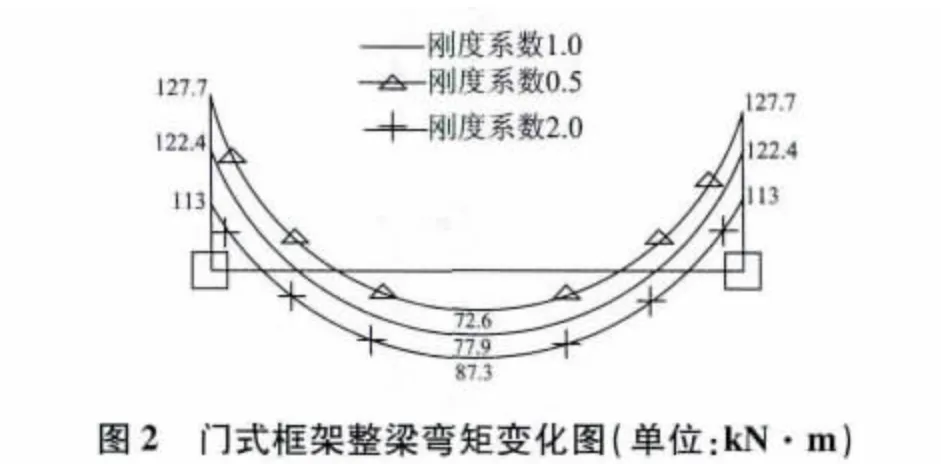
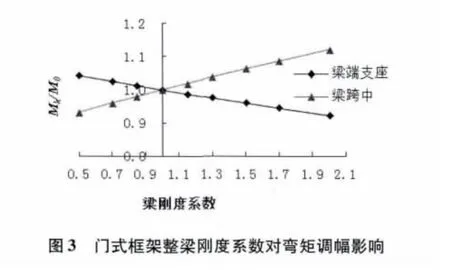
通過表1 和圖2、圖3 得出結論:門式框架梁，對于改變整個梁剛度對梁支座處負彎矩的折減的影響有以下幾點。

(1)梁端支座處負彎矩的絕對值隨著梁剛度系數的增大而減小，即δ'=Mk/M0隨著剛度系數的增大而減小。當剛度系數為0.5 時，梁端支座處δ'=1.043 3;當剛度系數取2.0 時，梁端支座處δ'=0.923 2;

(2)跨中正彎矩隨著梁剛度系數的增大而增大，即δ' 隨著梁剛度系數的增大而增大。當剛度系數為0.5 時，梁端支座處δ'=0.932;當剛度系數取2.0 時，梁端支座處δ'=1.120 7。

3.1.2 門式框架分段梁

圖4 門式框架分段梁各段剛度系數圖

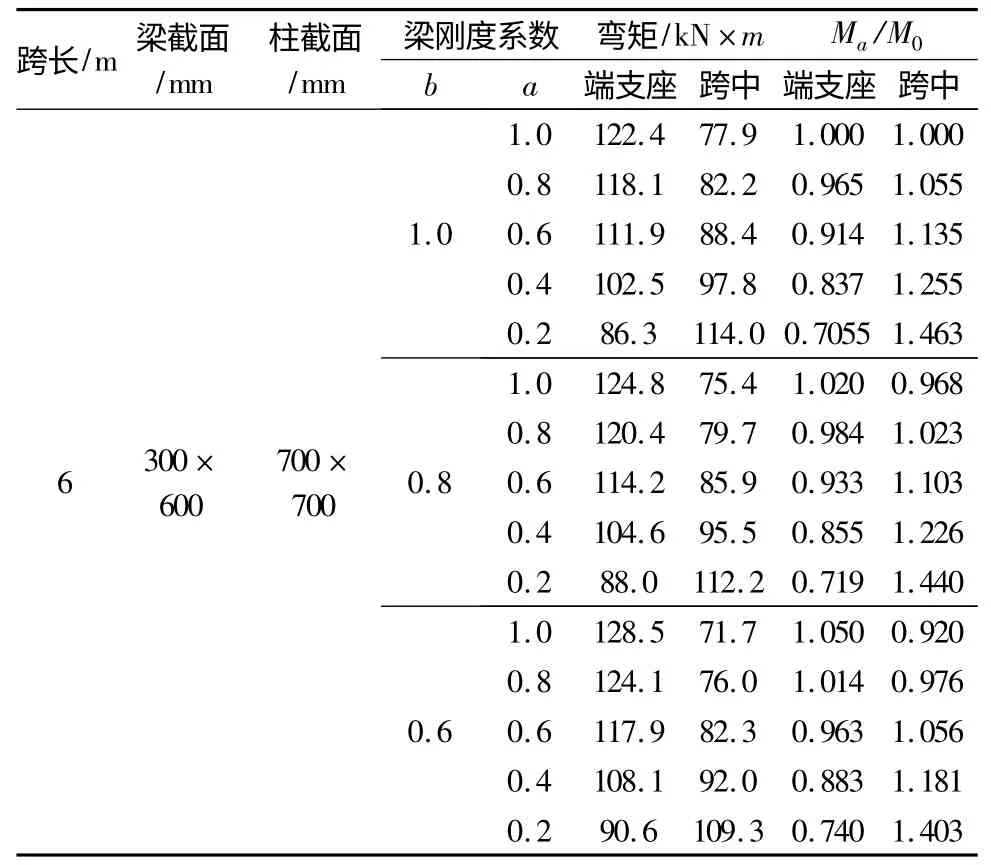
表2 門式框架梁分七段彎矩變化表

梁分七段，改變其梁端支座處梁段的剛度系數和梁跨中段的剛度系數，計算分析其剛度系數變化對支座負彎矩和梁跨中彎矩影響，得出結論:

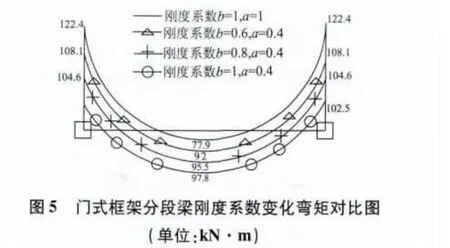
(1)由圖5 可見分段梁改變梁端支座處剛度系數可以實現梁彎矩調幅，且跨中間段剛度系數分別為1.0、0.8、0.6 時，梁兩端支座剛度系數為0.4 時，可以分別使得梁端支座彎矩調幅16.3%，14.5%，11.7%。

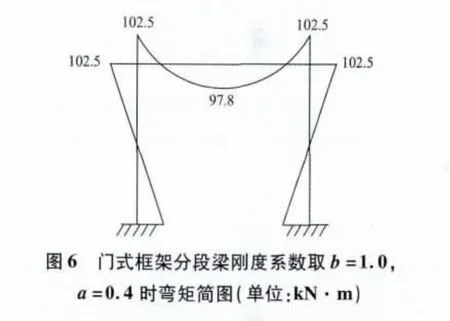
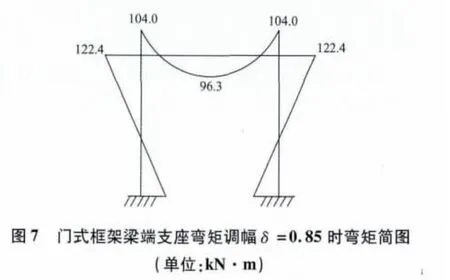
(2)對比圖6 和圖7 可見，傳統的梁彎矩調幅只對梁進行調幅，并未調節柱，梁柱節點顯然不平衡;而分段梁對端支座處梁進行剛度調節，既可以實現梁彎矩調幅，又可以使得梁柱節點平衡。

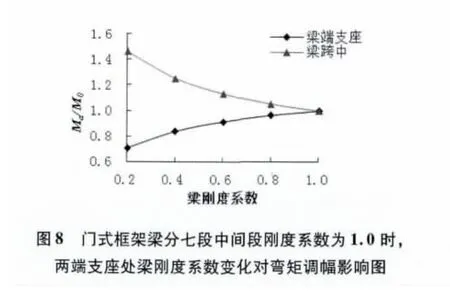
(3)如表2 和圖8，當梁平分成七段，梁中間跨剛度系數為1.0，其他段的剛度系數都為1.0，只改變梁兩端支座處梁段的剛度系數，從1.0 變化到0.2，此時隨著梁兩端支座處梁段剛度系數減小，梁端支座負彎矩的絕對值減小，即δ1.0=Ma/M0隨之減小;而跨中正彎矩隨著剛度系數的減小而增大，即δ1.0隨之增大。當端支座處梁段剛度系數a 取1.0 時，兩端支座和跨中δ1.0=1.0;當端支座處梁段剛度系數a 取0.2時，兩端支座δ1.0=0.705 1，跨中δ1.0=1.463 4。

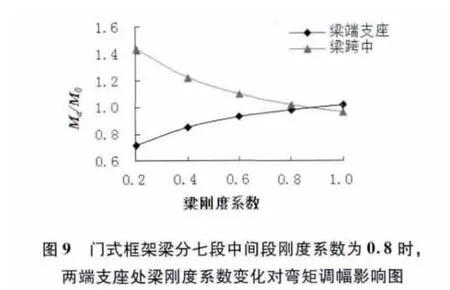
(4)由表1 和圖9 可見，梁平分七段，梁中間跨段剛度系數為0.8，其他段剛度系數都為1.0，只改變梁兩端支座處梁段的剛度系數，從1.0 變化到0.2，此時隨著梁兩端支座處梁段剛度系數減小，梁端支座負彎矩的絕對值減小，即δ0.8隨之減小;跨中正彎矩隨之增大。當端支座處梁段剛度系數a 取0.8時，兩端支座δ0.8=1.019 6，跨中δ0.8=0.967 9;當端支座處梁段剛度系數a 取0.2 時，兩端支座δ0.8=0.719 0，跨中δ0.8=1.440 3。

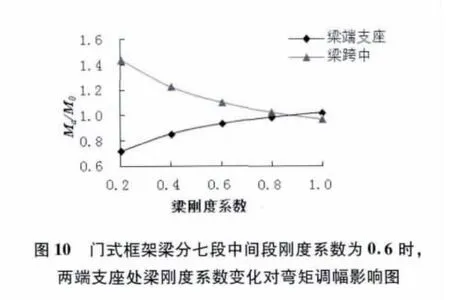
(5)如圖10 所示，梁中間跨段剛度系數b 為0.6，其他段剛度系數都為1.0，只改變梁兩端支座處梁段的剛度系數，從1.0 變化到0.2，此時隨著梁兩端支座處梁段剛度系數減小，梁端支座負彎矩的絕對值減小，即δ0.6隨之減小;跨中正彎矩隨之增大。當端支座處梁段剛度系數a 取1.0 時，兩端支座δ0.6=1.049 8，跨中δ0.6=0.920 4;當端支座處梁段剛度系數a 取0.2 時，兩端支座δ0.6=0.740 2，跨中δ0.6=1.403 1。

(6)由圖8、圖9、圖10 可見，當中間跨段剛度系數取不同值時，其端支座δ 曲線與跨中相交點不同，并且隨著跨中段剛度系數減小，相交點處橫坐標值越小。

(7)由表格2 和圖8、圖9、圖10 可知，相同情況下，跨中梁段剛度系數分別取1.0、0.8、0.6 時，所得端支座和跨中彎矩并不相等，且端支座彎矩隨著中間段梁剛度系數減小而相對增加，跨中彎矩相對減小。

3.2 三跨剛架

3.2.1 三跨剛架無分段梁

圖11 三跨剛架整梁模型圖

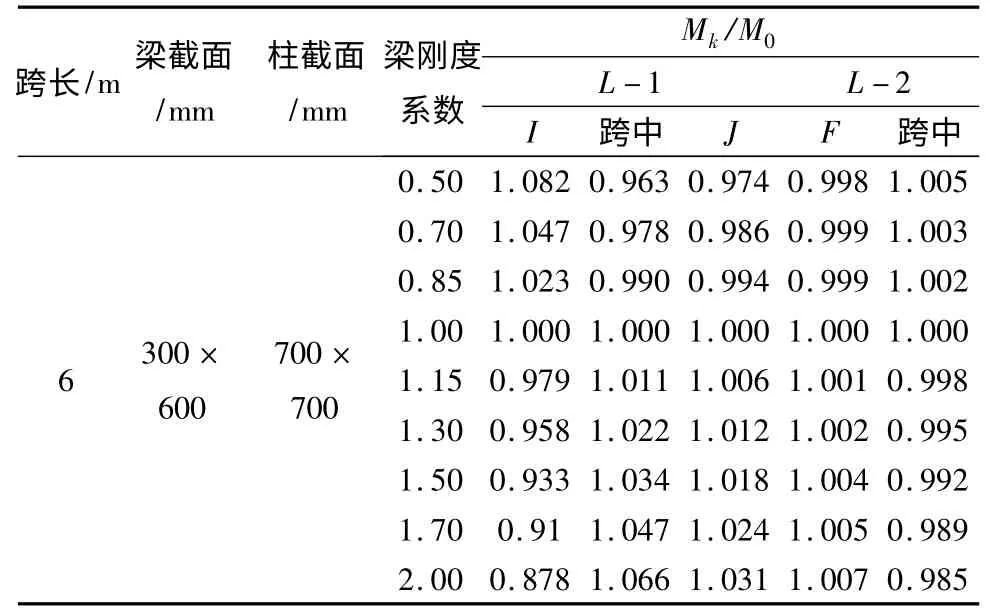
表3 三跨剛架整梁彎矩調幅變化表(單位:mm)

如圖12 所示整梁剛度的調節并不能實現梁彎矩的調幅。

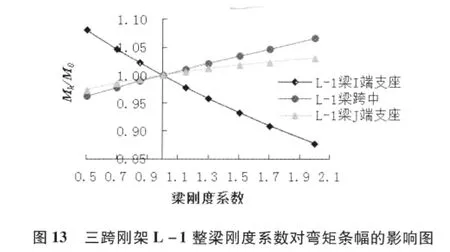
由圖13 得出結論:對于三跨剛架，隨著剛度系數的增大，L－1 梁I 端支座處負彎矩絕對值減小;J端支座負彎矩絕對值增大，但是增大的幅度都很小;跨中正彎矩逐漸增大;

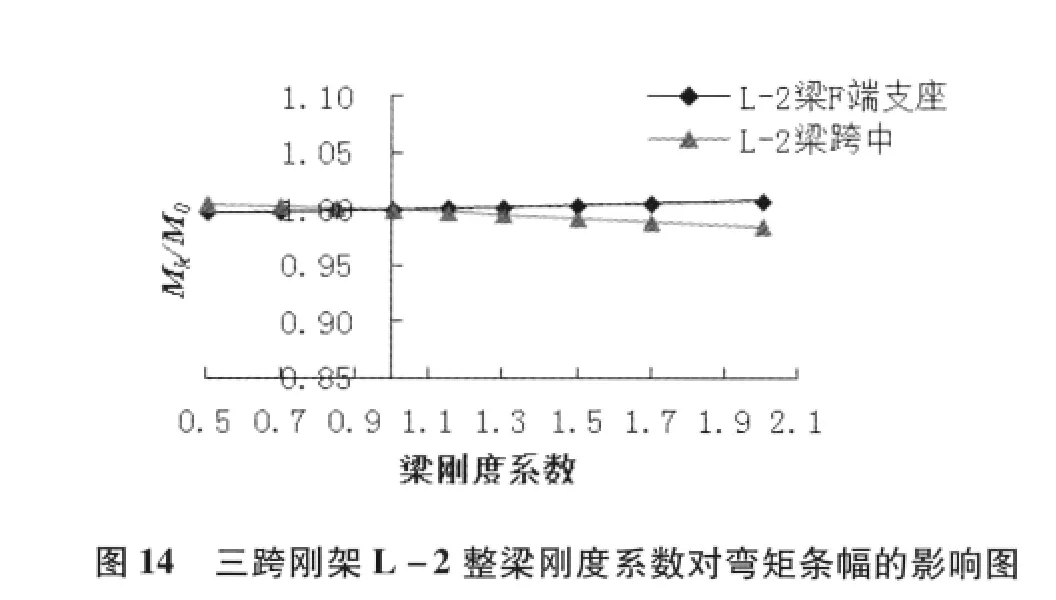
由圖14 可見隨著梁剛度系數的增大，L－ 2 梁F 端支座負彎矩絕對值逐漸增大，而中間跨跨中正彎矩逐漸減小。

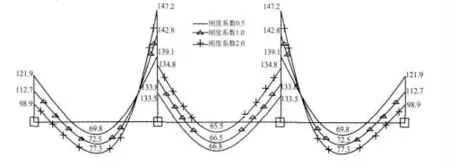
圖12 三跨剛架整梁剛度系數變化彎矩對比圖(單位:kN·m)

3.2.2 三跨鋼架分段梁

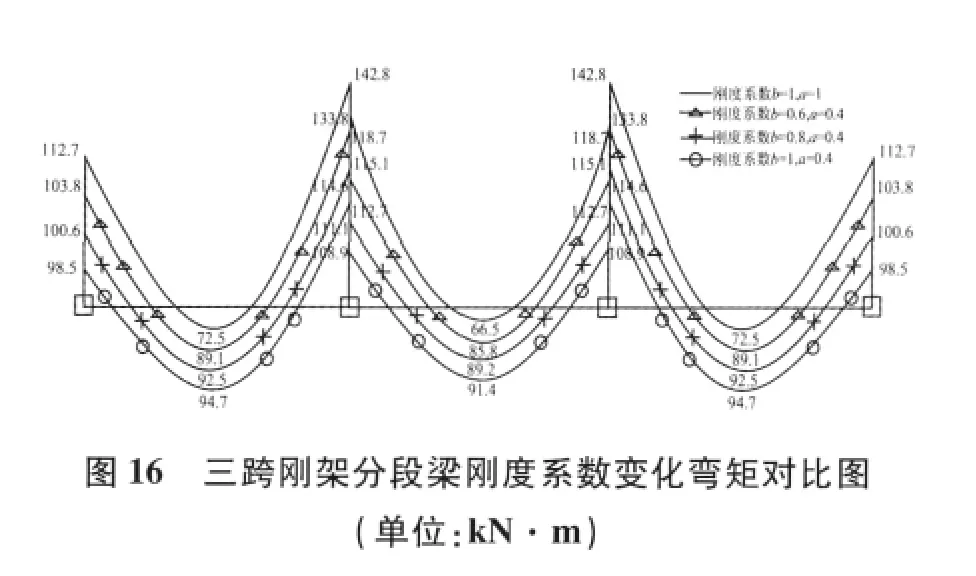
通過以上對三跨梁進行分段，調節剛度系數分析，得出結論:

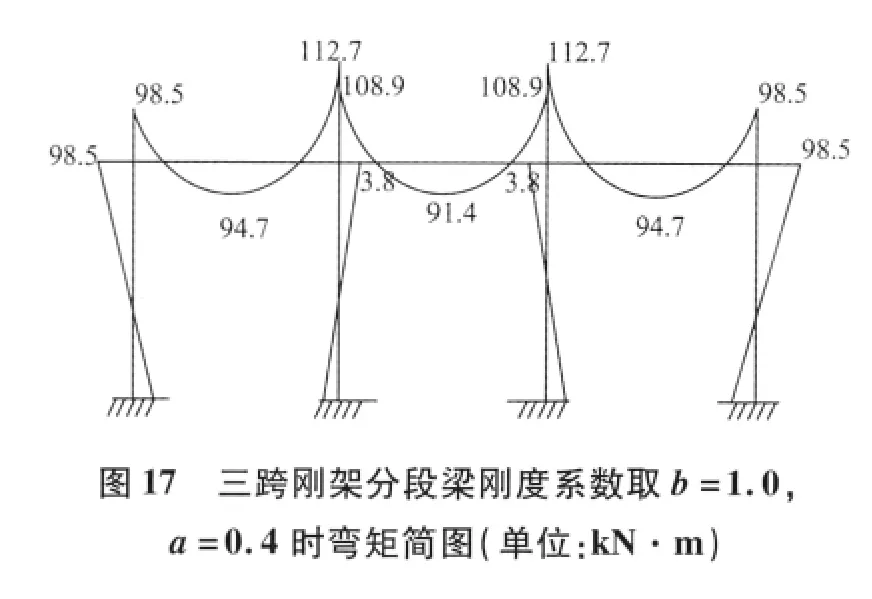
(1)由圖17 可見分段梁改變梁端支座處剛度系數可以實現梁彎矩調幅，且跨中間斷剛度系數分別為1.0、0.8、0.6 時，梁兩端支座剛度系數為0.4時，各個梁調幅大小不一。

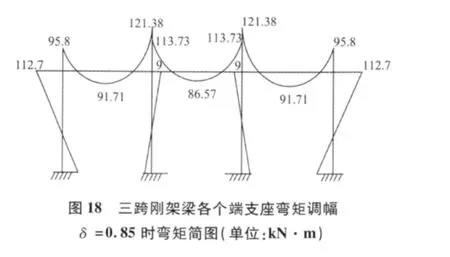
(2)對比圖18 和圖19 可見，對于三跨剛架梁，傳統的梁彎矩調幅只對梁進行調幅，并未調節柱，梁柱節點顯然不平衡;而分段梁對端支座處梁進行剛度調節，既可以實現梁彎矩調幅，又可以使得梁柱節點平衡。

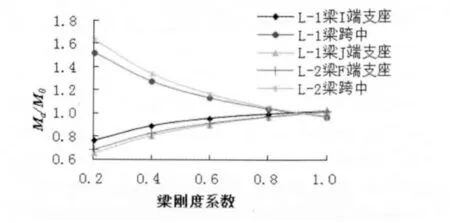
圖20 三跨剛架梁分七段中間段剛度系數為0.8 時，兩端支座處梁剛度系數變化對彎矩調幅影響

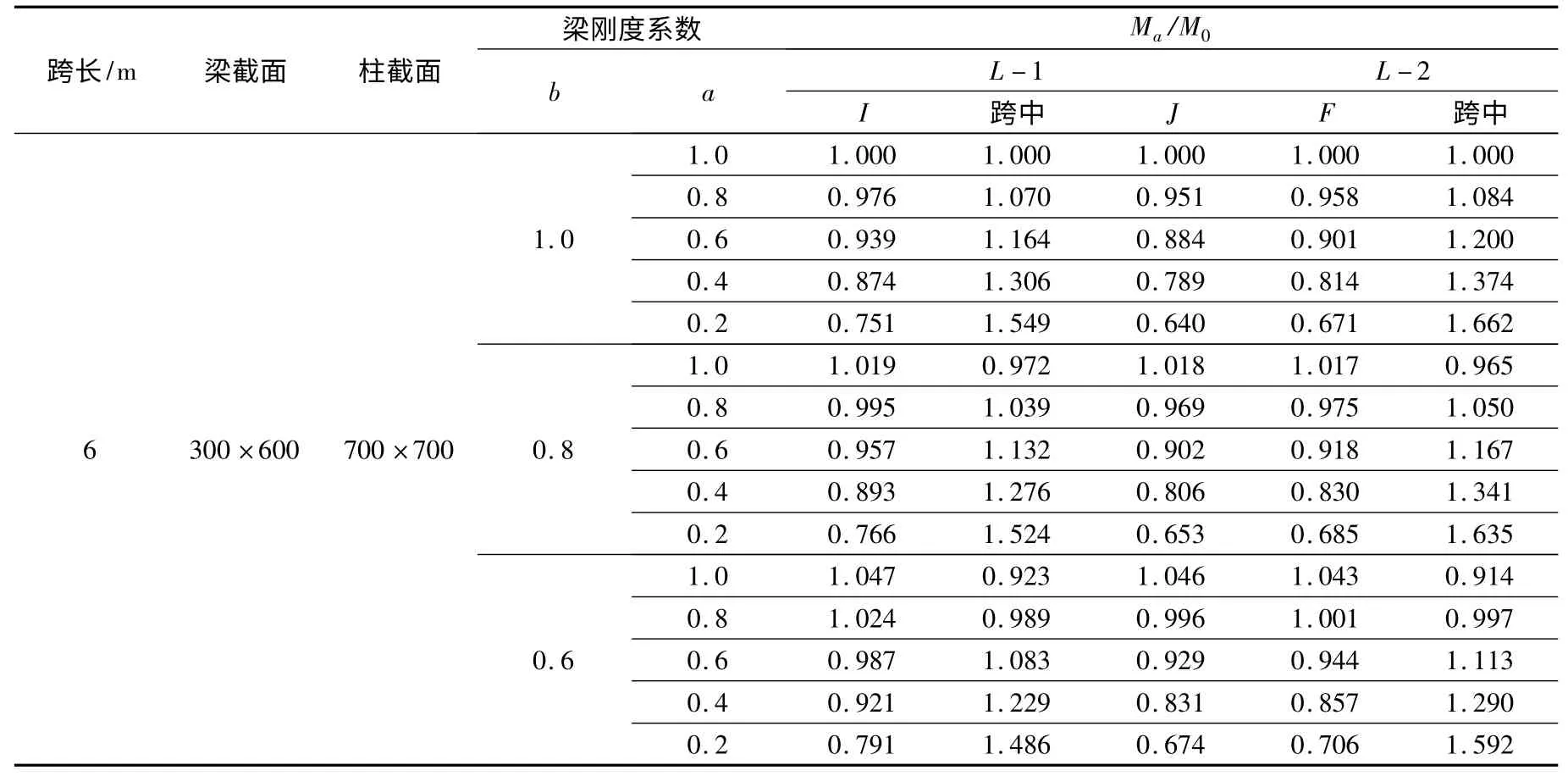
表4 三跨剛架梁分七段彎矩調幅變化表 (單位:mm)

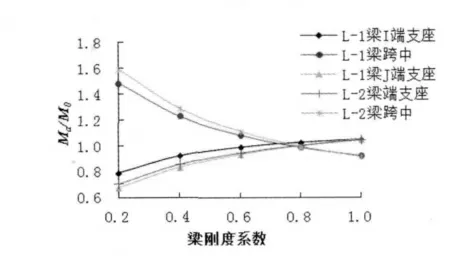
圖21 三跨剛架梁分七段中間段剛度系數為0.6 時，兩端支座處剛度系數變化對彎矩調幅影響

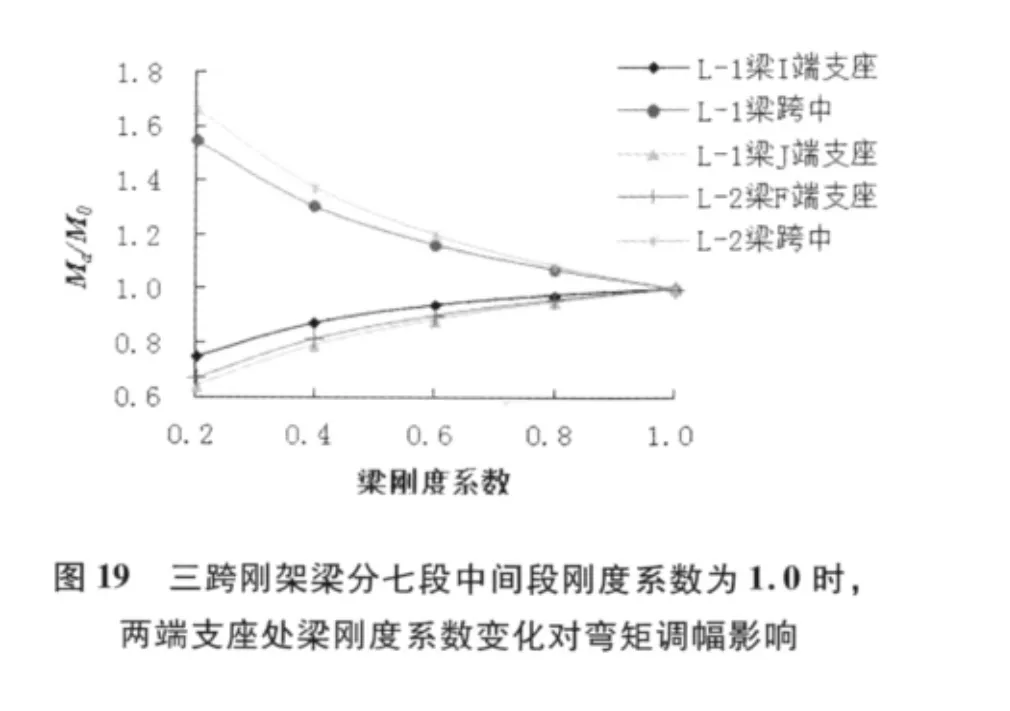
(3)如表4 和圖20 所示，當各個梁平分成七段，梁中間跨剛度系數為1.0，其他段的剛度系數都為1.0，只改變梁兩端支座處梁段的剛度系數，從1.0 變化到0.2，此時隨著梁兩端支座處梁段剛度系數減小，L－1 梁端支座I、J 和L－2 梁F 端負彎矩的絕對值減小，即δ1.0=Ma/M0隨之減小;而各個梁跨中正彎矩隨著剛度系數的減小而增大，即δ1.0隨之增大;

(4)通過圖21 可得出結論:情況與中間跨段剛度系數為1.0 時同，只是改變跨中段剛度系數為0.8，此時各個梁的δ0.8與δ1.0的變化情況相同，都是隨著剛度系數減小，各梁端支座δ0.8逐漸減小，跨中δ0.8逐漸增大;

(5)由圖22 可見，當分段梁中間段剛度系數為0.6 時，L－1 梁I、J 端支座和L－2 梁F 端支座負彎矩的絕對值，隨著梁兩端支座處梁段剛度系數的減小而減小;L－1 梁和L－2 梁跨中彎矩都隨之減小而增大，只是增大的速度各不相同;

(6)通過圖20、圖21、圖22 可見，相同情況下，L－1 梁I，J 端支座處和L－2 梁F 端支座處δ 隨梁剛度變化的趨勢雖然相同，但是變化的速度并不相同，相比之下，L－1 梁J 端變化最大，L－2 梁F 端變化最緩和。而L－1 梁跨中和L－2 跨中相比，L－1梁跨中要比L－2 梁跨中δ 隨梁剛度系數變化而變化的相對緩和;

(7)對比圖20、圖21、圖22，得出結論:當中間跨段剛度系數取不同值時，各個梁端支座δ 曲線與跨中δ 曲線相交點不同，并且隨著跨中段剛度系數減小，相交點處橫坐標值越小。當中間跨梁段剛度系數取1.0 時，相交點橫坐標即為1.0;當中間跨梁段剛度系數取0.8 時，相交點橫坐標大概在0.8～1.0之間;當中間跨梁段剛度系數取0.6 時，相交點橫坐標大概在0.6～0.8 之間。

3.3 簡單三維框架

3.3.1 簡單三維框架無分段梁

圖22 簡單三維框架整梁模型圖

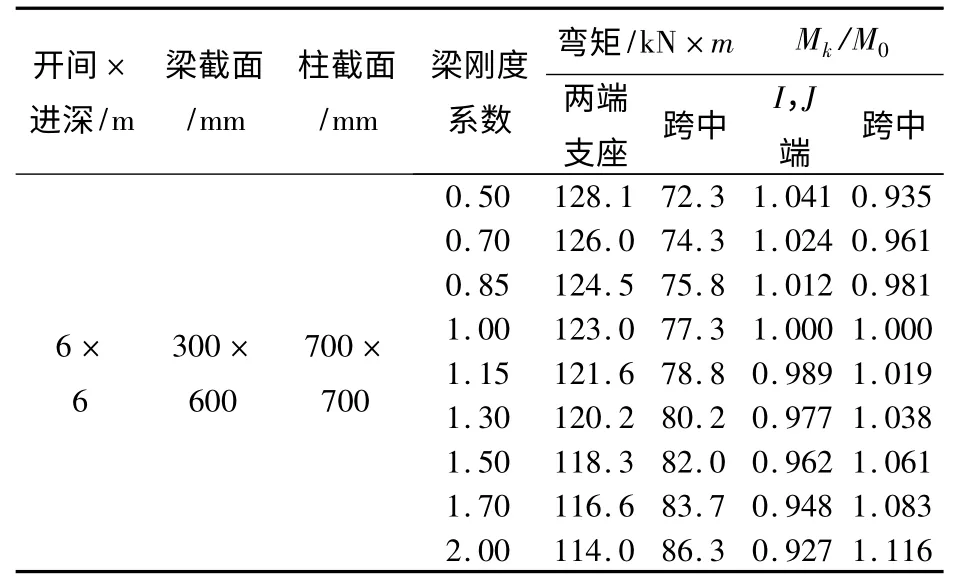
表5 簡單三維框架整梁彎矩調幅變化表

由于結構是對稱結構，荷載為對稱荷載，所以框架各個梁上的內力值相等，其各個梁剛度變化對梁彎矩調幅影響規律和門式框架梁基本相同。由表5 可見，簡單框架各個梁上端支座負彎矩的絕對值隨梁剛度系數變大而減小，而跨中正彎矩值增大。

3.3.2 簡單三維框架分段梁

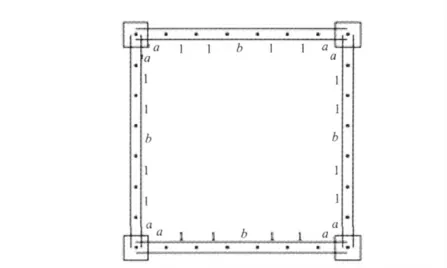
圖23 簡單三維框架分段梁各段剛度系數圖

通過對比簡單三維框架和門式框架梁，簡單三維框架各個梁的端支座和跨中δb與門式框架梁變化規律相同。

3.4 3 ×3 三維框架

3.4.1 3 ×3 三維框架無分段梁

圖24 3 ×3 三維框架整梁模型圖

通過對3 ×3 三維框架整梁和三跨剛架整梁的對比，可見由于對稱性，框架各個整梁剛度變化對梁彎矩調幅的影響規律與三跨剛架梁基本相似。由表7 可見，隨著梁剛度系數的增大，I 端支座處負彎矩絕對值隨著梁剛度系數增大而減小;J 端和F 端支座負彎矩絕對值，隨剛度系數增大而增大，但是增大的幅度都很小;隨著剛度系數的增大，邊跨跨中正彎矩逐漸增大，中間跨跨中正彎矩逐漸減小。

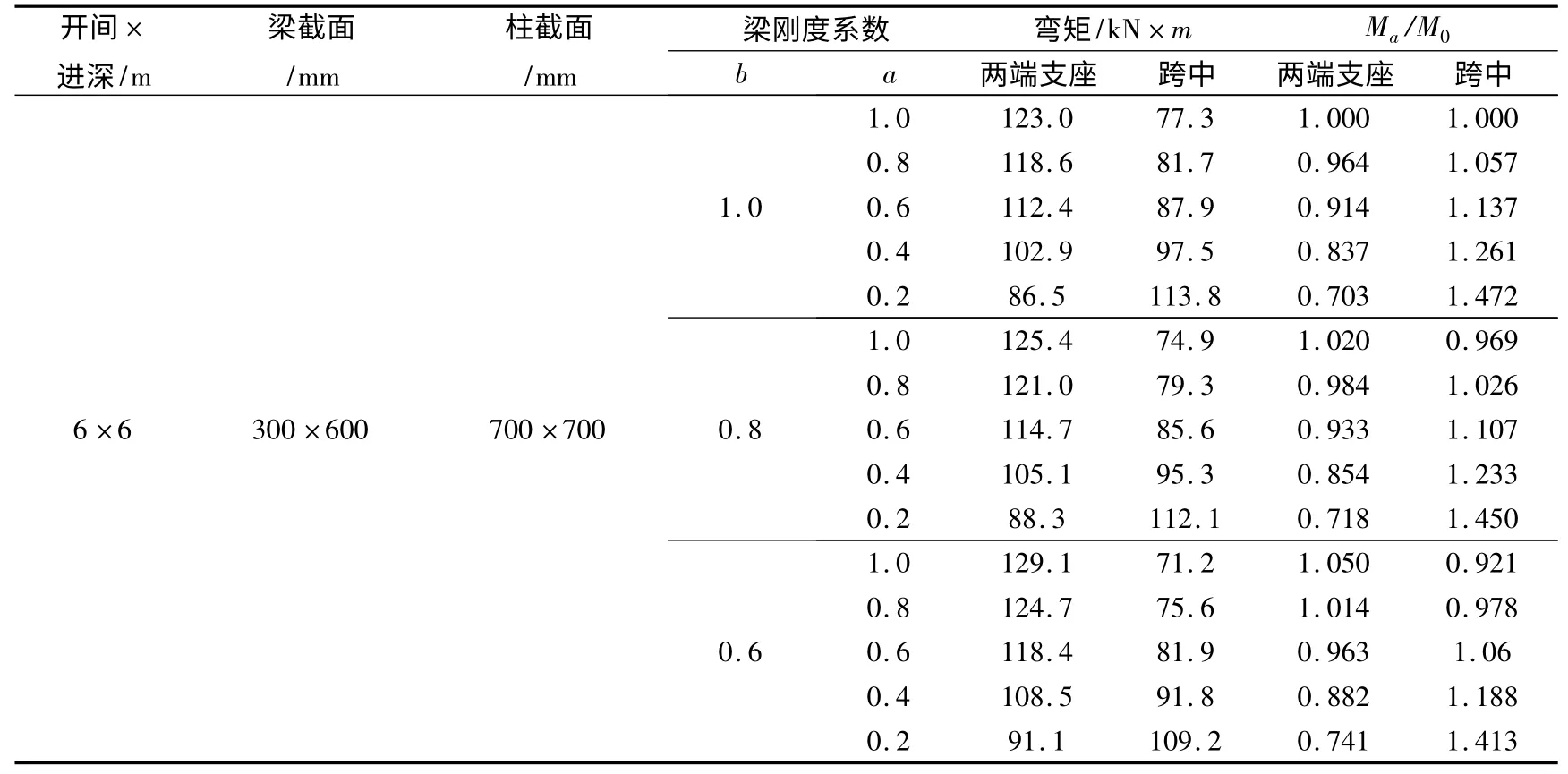
表6 簡單三維框架梁分七段彎矩調幅變化表

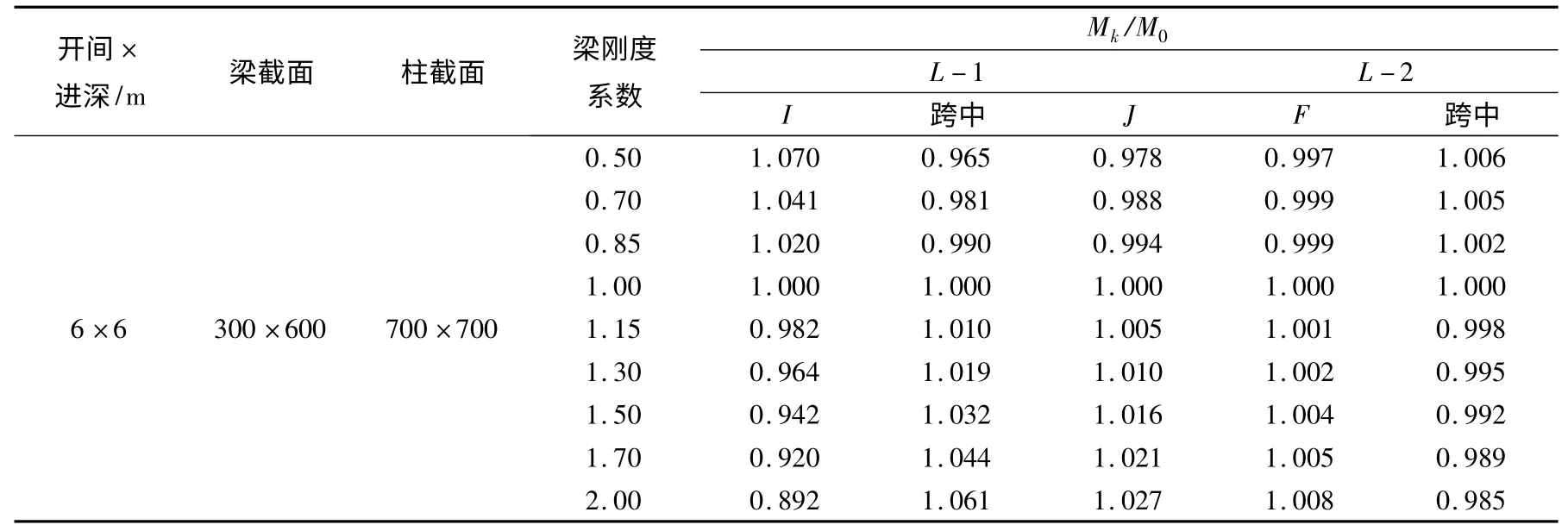
表7 三維框架整梁彎矩調幅變化表 (單位:mm)

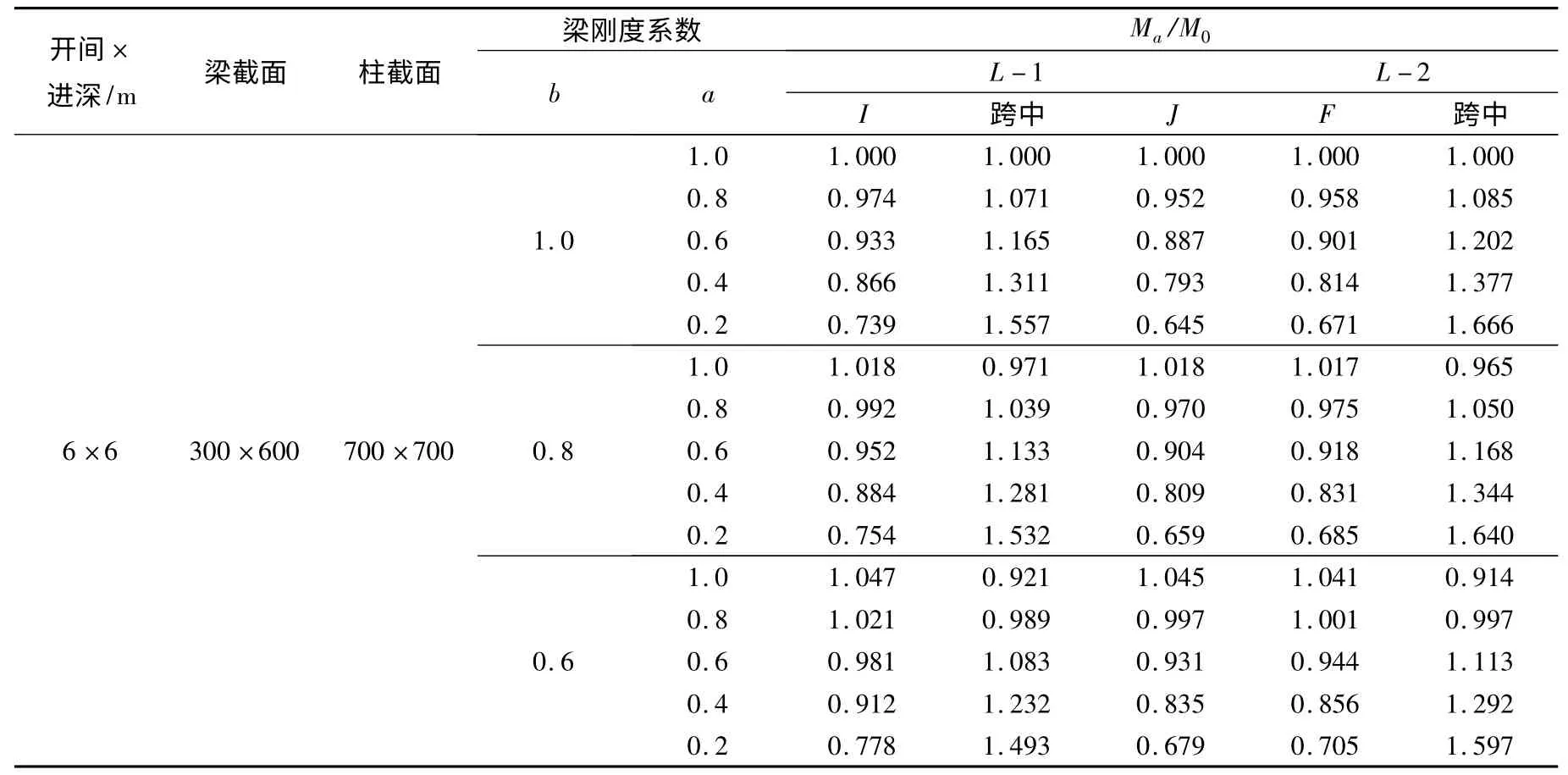
表8 三維框架分段梁彎矩調幅變化表 (單位:mm)

3.4.2 3 ×3 三維框架分段梁

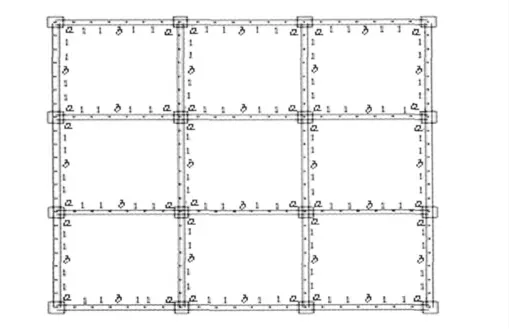
圖25 3 ×3 三維框架分段梁各段剛度系數圖

通過對3 ×3 三維框架分段梁和三跨剛架分段梁的對比，可見由于對稱性，3 ×3 三維框架分段梁剛度變化對彎矩調幅的影響規律與三跨剛架分段梁基本相同。

3.5 擬合分段梁梁剛度變化對彎矩調幅影響關系式

綜合上述，考慮各個模型分段梁，其中間梁段剛度系數b 取1.0，兩端支座處剛度系數a 變化對各種模型中各個梁端支座彎矩調幅的影響，擬合梁剛度變化對彎矩調幅的影響關系式。見圖26。由圖26 可見彎矩調幅與分段梁端支座處梁剛度變化的關系式為:

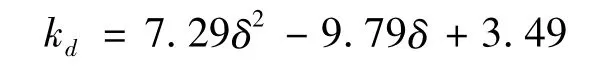
其中:

δ—梁端支座彎矩條幅系數;

kd—分段梁端支座處剛度系數。

按上式計算所得調幅系數與梁端剛度系數對應值見表9

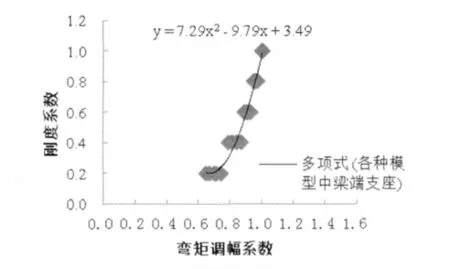
圖26 梁剛度變化與彎矩調幅的關系圖

表9 調幅系數與梁端剛度系數對應表

4 結論

通過以上分析計算可見，梁端負彎矩調幅與整梁剛度系數之間的關系，并不是呈現一定的正負關系，而是根據各個梁的不同，影響規律和影響大小都不相同。分段梁改變端支座處梁段的剛度系數與彎矩調幅成一定的關系，即兩端支座處梁段的剛度系數a 取值越小，端支座彎矩調幅δ 值越小，和實際假設情況相符，且可以使得梁柱節點內力平衡。不考慮梁跨中開裂，擬合兩端支座剛度變化對彎矩調幅的影響關系式為:kd=7.3δ2－9.8δ +3.5。但是由于調幅δ 限于1～0.75。所以kd的取值應大概在1～0.3 之間。

［1］貢金鑫，魏巍巍等.中美歐混凝土結構設計［M］.北京:中國建筑工業出版社，2007 年12 月.

［2］中國工程建設標準化協會《鋼筋混凝土連續梁和框架考慮內力重分布設計規程》(CECS51:93)，重慶建筑大學，1993.

［3］Building Code Requirements for Structural Concrete (ACI 318－08)and Commentary (ACI 318R－08)［S］.ACI Committee 318，2008.

［4］鄧宗才，鋼筋混凝土連續梁彎矩調幅法的研究［J］.建筑結構，1997 年08 期.

［5］清華大學土木與環境工程系，山西省建筑科學研究所.鋼筋混凝土連續粱彎矩調幅限值的試驗研究［J］.建筑技術通訊，1981 年01 期.