物理化學模型對高溫流場等離子體分布的影響

高鐵鎖，董維中，丁明松，江 濤

（中國空氣動力研究與發展中心，四川 綿陽 621000）

0 引 言

高超聲速飛行器在大氣層中以高超聲速飛行時，由于激波和粘性作用，波后氣體溫度超過10000K，這時高溫空氣發生振動能量激發、離解和電離等化學反應過程，成為部分電離氣體，并在飛行器周圍形成高溫等離子體流場。由于飛行器周圍等離子體分布直接關系到電磁波的傳輸特性［1－6］，因此研究高超聲速飛行器流場中等離子體的產生機理和分布特性，對于高超聲速飛行器的無線電通信技術的發展具有重要意義。

飛行器周圍流場等離子體分布與飛行高度、速度、姿態和飛行器外形尺寸、表面材料催化特性等多種因素有關。采用求解N－S方程的數值方法對其進行模擬時，除了需要解決熱化學非平衡源項引起的剛性問題外，還需要選取合適的化學反應模型，因為計算中考慮的組分越多計算越復雜，對計算資源的要求越高，而采用含組分少的簡化模型有時不能全面反映高溫流動中等離子體的產生機制，影響數值模擬的精準度［7］。數值模擬高溫空氣電離流動常用的有7組分和11組分化學反應模型［8－10］，如得到廣泛應用的Blottner的7組分反應模型［8］和Dunn與Kang的11組分反應模型［9］等。由于高溫電離流動問題的復雜性，目前還沒有明確和統一的化學反應模型選取準則。另外，準確模擬高溫電離流動還需要研究熱力學非平衡效應及壁面催化和壁面溫度等邊界條件的影響［11－14］。高溫氣體熱力學非平衡涉及分子振動能級之間和振動與平動能級之間的能量交換以及振動－離解耦合效應等復雜物理化學過程，對熱力學非平衡效應的數值模擬一直是高溫氣體動力學領域的前緣課題之一［7，11，13－14］。本文針對復雜升力體外形，采用數值模擬方法，研究不同反應模型和非平衡氣體模型以及壁面催化和溫度條件對流場等離子體數值模擬結果的影響。

1 復雜外形戰術彈頭非平衡流場的計算方法

1.1 控制方程

控制方程是三維熱化學非平衡N－S方程，其無量綱化形式如下［13］：

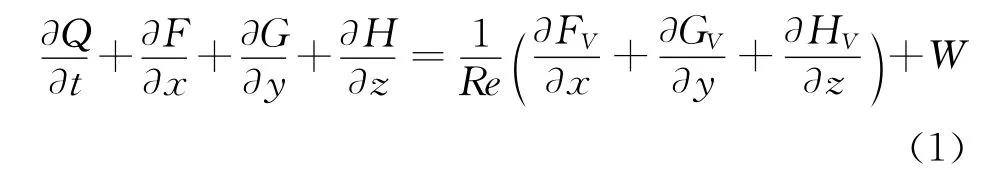
其中Q＝（ρi，ρEV，ρ，ρu，ρv，ρw，ρE）T，W＝（wi，wV，0，0，0，0，0）T，ρi是組分密度，EV是分子組分的總振動能量，wi和wV是化學非平衡源項和振動非平衡能量源項。

1.2 熱化學模型

采用11組分（O2，N2，NO，O，N，NO＋，e，O＋2，，O＋，N＋）和7組分（O2，N2，NO，O，N，NO＋，e）化學反應模型，具體反應式及反應速率常數見文獻［9，13］。對于正向和逆向反應速率常數為kfi與kbi，第i個反應表達式（2）對應的第j個組分的化學反應的生成源項見式（3）：

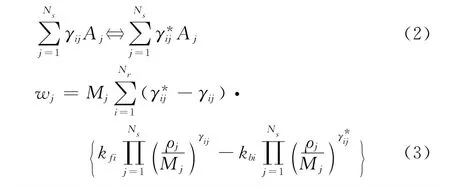
振動非平衡能量源項為兩項之和，一項是平動能與振動能的交換項，另一項是化學反應中分子離解引起的振動能量的變化項，其表達式如下［13］：

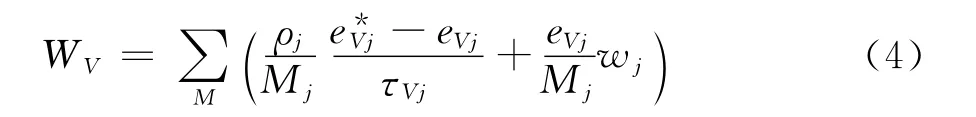
1.3 壁面催化條件

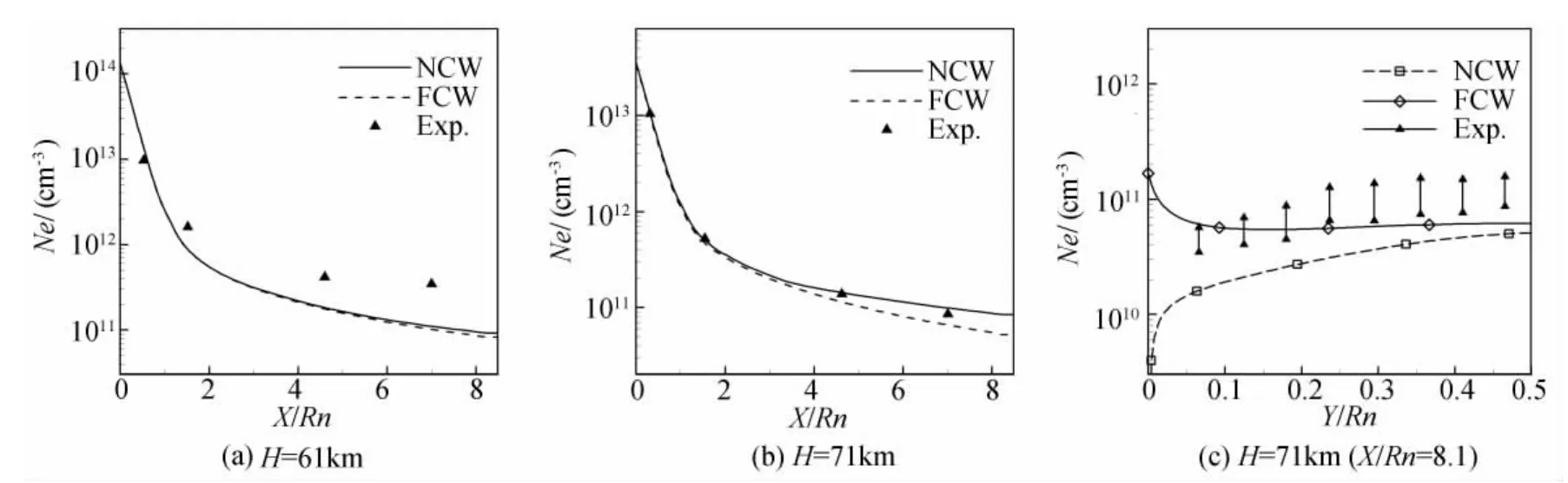
圖1 計算與飛行測量電子數密度分布比較Fig.1 Comparison of computation with flight experiment

1.4 數值方法

采用全隱式LU－SGS數值方法對方程（1）求解［13－15］，無粘項的離散采用Yee的TVD格式［15－16］，粘性項的離散采用中心差分方法。

2 計算結果分析

2.1 RAM－C模型繞流等離子體分布的比較

RAM－C模型為球錐體，球頭半徑Rn＝0.1542m，半錐角θ＝9°，長度L＝1.295m；飛行條件：U∞＝7650.0m／s，H＝61km、71km，壁面溫度TW＝1500K。

采用7組分化學反應模型和兩溫度熱力學非平衡模型，考慮完全非催化（NCW）和完全催化（FCW）壁面條件，主要考核電子數密度分布情況。圖1給出了兩個飛行高度的電子密度分布與文獻［14］的飛行數據比較，其中圖1（a）和圖1（b）對應流場剖面電子數密度峰值沿軸向分布。可以看出，電子密度計算與飛行測量數據符合較好，誤差只在3倍左右。飛行速度不變，隨著高度的降低，流動越接近熱化學平衡態，完全非催化和完全催化條件的計算結果越接近。從圖1（c）可見，催化條件對X／Rn＝8.1處的電子數密度徑向分布具有較大影響。總體上看，完全催化壁條件的計算結果更接近飛行測量值。

2.2 化學反應模型和非平衡模型對流場等離子體分布的影響

計算外形為升力體外形，計算高度60km，飛行馬赫數為20，攻角12°。認為壁面組分滿足完全非催化壁面條件，壁面溫度取600K。P1和P2分別表示靠近升力體頭部和底部的兩個剖面位置。下面主要給出升力體對稱面上迎風區的計算結果。

圖2給出了采用7組分與11組分反應模型計算的壁面離子和電子數密度沿軸向分布的比較。可以看出，11組分化學反應模型的電子數密度計算值高于7組分的計算值，二者在升力體球頭區域差別較大，最大相差一個量級，隨著流動向下游發展，其差別越來越小。頭部流場溫度最高達10000K以上（見圖3a），此時除了考慮NO＋離子，化學反應模型中還應考慮O＋的作用。NO＋主要由O與N原子的締合電離反應機制產生，O＋則主要由O原子與電子及其它組分的碰撞反應機制產生。由于頭部流動區域溫度較高，使得O原子電離起主導作用，O電離生成O＋對電子數密度的貢獻超過NO電離生成NO＋的貢獻，而在下游區域流場溫度逐漸降低，NO的化學電離逐漸起主導作用，7組分和11組分兩種反應模型的計算結果也逐漸趨于一致。高溫流動中化學電離過程除了與溫度密切相關外，還與流動壓力與非平衡馳豫過程有關，壓力有抑制電離和離解的作用。

圖3和圖4給出P1和P2剖面的溫度、離子組分質量分數和電子數密度分布。其中圖3（a）和圖4（a）給出完全氣體模型（PG）和非平衡氣體模型的流場溫度的比較，可以看出，完全氣體模型的流場溫度和激波脫體距離的計算值明顯高于考慮真實氣體效應的非平衡氣體模型的計算值。這是因為分子離解和電離等吸熱反應過程使得氣體流場溫度降低，密度增加，而化學過程對流動壓力影響很小，故使得激波脫體距離減小。從圖3和圖4還可以看出，在升力體的頭部流場區域（P1剖面），由于流場溫度很高，兩種化學反應模型計算的剖面電子數密度差別很大，此時電子主要來源于O電離生成O＋的化學過程，然后以次是氣體分子生成NO＋、O＋2和N＋2的化學過程。在升力體的后部（P2剖面），由于流場溫度降低，二者的剖面電子數密度分布差別變得很小，此時O＋的作用較頭部明顯減弱。

圖5給出P1和P2流場剖面的溫度與電子數密度分布云圖。可見，迎風面的等離子體厚度明顯小于背風面的等離子體厚度，隨著流動從升力體頭部（P1剖面）發展到后部（P2剖面），剖面溫度最大值從12144K降低到4118K，剖面最大電子數密度從5.98×1014／cm3衰減到2.49×1010／cm3，但等離子體厚度明顯增加，并且在升力體對稱面附近等離子體相對較厚，沿展向逐漸變薄。

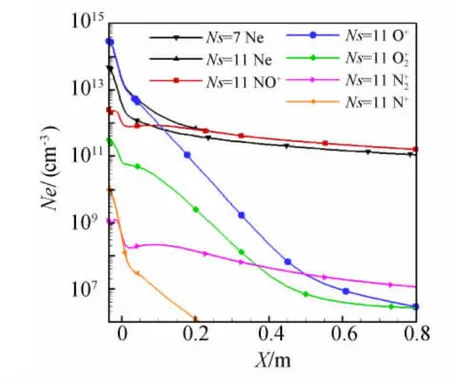
圖2 壁面離子及電子數密度分布Fig.2 Distribution of ions andelectron number densities on the wall

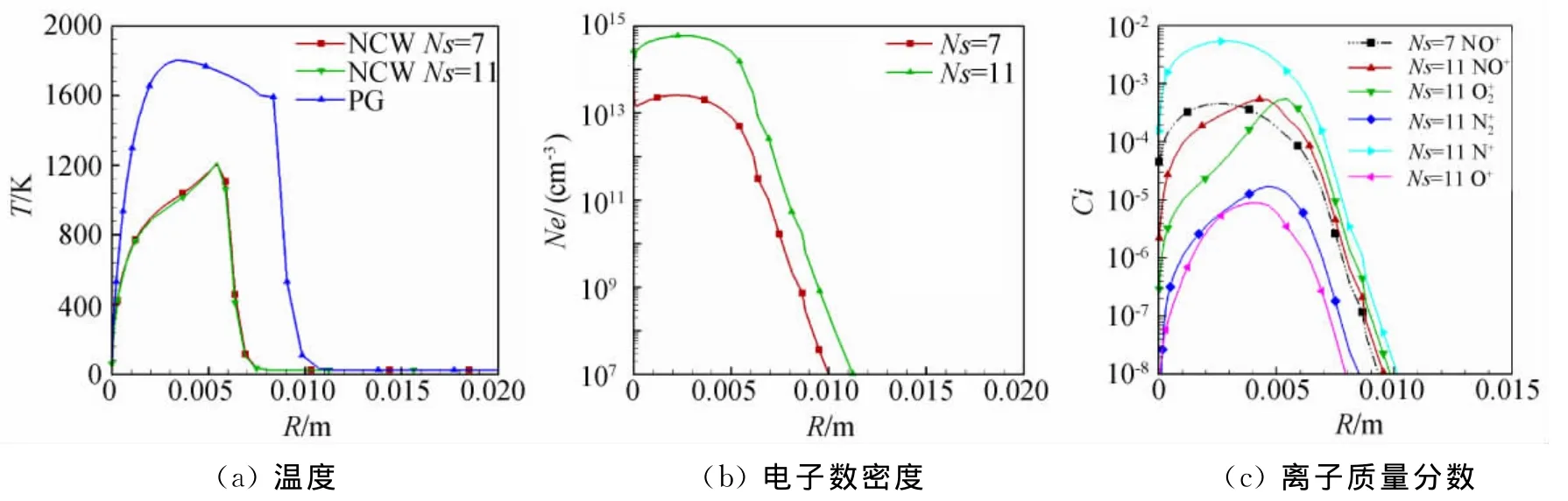
圖3 P1剖面流場參數分布Fig.3 Distribution of flow parameter of P1profile

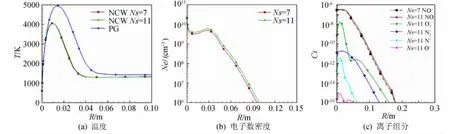
圖4 P2剖面流場參數分布Fig.4 Distribution of flow parameters of P2profile

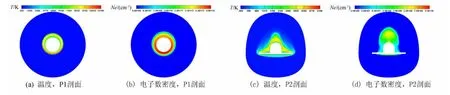
圖5 剖面溫度與電子數密度云圖（Ns＝11）Fig.5 Temperature andelectron number densities contours

圖6給出了采用化學非平衡（CNeq）和熱化學非平衡模型（TCNeq）計算的頭部軸線溫度和電子數密度分布，可見在壁面附近區域，兩種模型的計算結果一致，但在離開壁面較遠的流動區域二者出現差異，化學非平衡模型計算的脫體距離較小，電子數密度衰減較快。熱化學非平衡模型中考慮了分子振動內能模式的非平衡馳豫過程和振動－離解耦合效應，目前此模型還在發展之中［7，14］，對其可靠性驗證還存在很大困難。

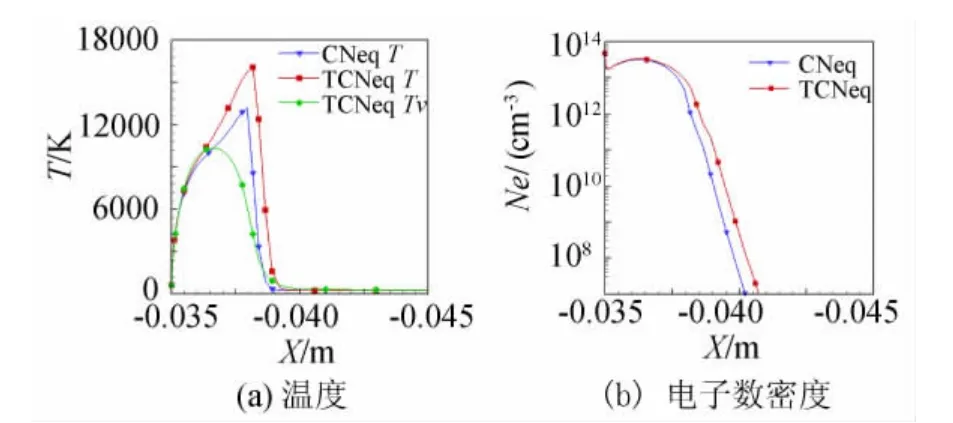
圖6 非平衡模型對溫度和電子數密度分布的影響Fig.6 Effects of nonequilibrimmodels on distribution of temperature and electron number densities

2.3 壁面條件對流場等離子體分布的影響

圖7（a）給出了不同壁面催化條件對P2剖面電子數密度分布的影響。這里沒有考慮NO＋等離子在壁面的催化復合反應，只是考慮了O和N原子在壁面的有限催化反應，并認為它們的壁面催化速率常數為5m／s。從圖7（a）可以看出，有限催化（KW＝5m／s）條件下，電子數密度計算值接近完全非催化壁面的計算結果。

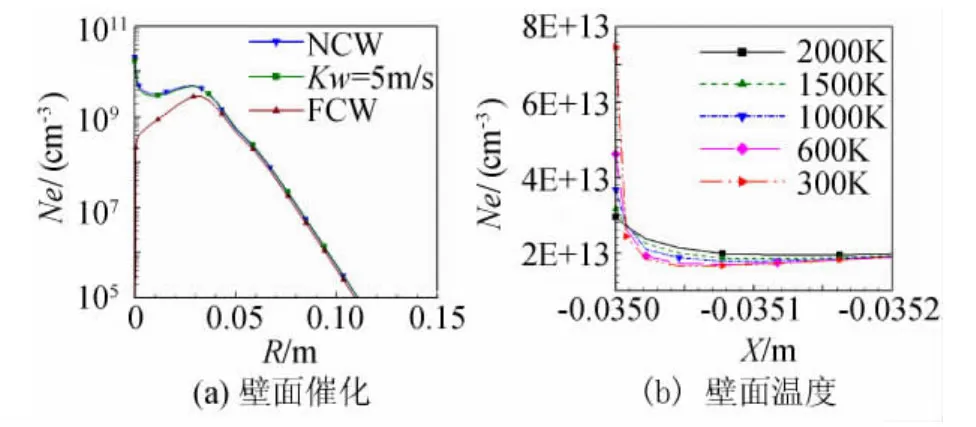
圖7 壁面條件對電子數密度分布的影響Fig.7 Effects of wall condition on distribution of electron number densities

圖7（b）給出了不同壁面溫度條件對頭部軸線流場電子數密度分布的影響。在完全非催化條件下，壁面溫度對電子數密度的影響主要集中在壁面附近很小的區域，貼近壁面的電子數密度以及電子數密度下降的梯度隨壁面溫度增加而減小。這里給出的結果是在同樣計算網格下獲得的，改變網格的數量和分布可能對計算結果產生不同程度的影響。

3 結束語

建立了復雜外形飛行器三維流場等離子體數值計算手段，實現了多塊網格并行運算功能，具備模擬復雜外形高溫流場電離效應、熱化學非平衡效應和壁面催化效應的能力。RAM－C模型繞流等離子體分布數值計算與飛行測量結果具有較好的一致性，表明了模型和數值方法的可行性。通過研究熱化學模型與壁面條件對升力體流場等離子體分布的影響，可得到以下兩點認識：

（1）準確數值模擬高溫流場等離子體分布，必須選擇合適的化學反應模型。化學反應模型的選取主要取決于流場等離子體的溫度和壓力，另外還與流動的非平衡松馳過程有關。對于本文研究的升力體外形和飛行狀態，頭部流場溫度最高達10000K以上，此時除了考慮NO＋離子，O＋離子對電子數密度的也有重要貢獻，化學反應模型中應包括O＋。采用不同非平衡氣體模型（熱化學非平衡或化學非平衡氣體模型）對高溫流場等離子體分布計算結果也會產生一定影響。

（2）壁面條件特別是壁面催化條件對流場等離子體分布具有較大影響。為了準確數值模擬升力體飛行器繞流等離子體分布，需要結合飛行和地面試驗測量結果，獲得可靠的材料催化特性和壁面溫度數據，在此基礎上對其周圍等離子體環境進行精細模擬。

［1］MUYLAERT J，CIPOLLINI F，et al.In－flight research on real gas effects using the ESA EXPERT vehicles［R］.AIAA 2003－6981，2003.

［2］MORABITO D，KORNFELD R，et al.The mars phoenix communications brownout during entry into the martian atmosphere［R］.IPN Progress Report，2009：42－179.

［3］HARTUNIAN R A，STEWART G E，et al.Implications and mitigation of radio frequency blackout during reentry of reusable launch vehicles［R］.AIAA 2007－6633，2007.

［4］鐘育民，諶明，盧滿宏，等.無線電波在再入等離子體中傳輸的衰減模型及仿真驗證［J］.遙測遙控，2010，31（2）：1－6.

［5］MATHER D E，PASQUAL J M，SILLENCE J P.Radio frequency（RF）blackout during hypersonic reentry［R］.AIAA 2005－3443.2005.

［6］STARKEY R P.Electromagnetic wave／magnetoactive plasma sheath interaction for hypersonic vehicle telemetry blackout analysis［R］.AIAA 2003－4167，2003.

［7］SCALABRIN L C，BOYD I D.Numerical simulation of weakly ionized hypersonic flow for reentry configurations［R］.AIAA 2006－3773，2006.

［8］BLOTTNER F G.Viscous shock layer at the stagnation point with nonequilibrium air chemistry［J］.AIAA Journal，1969，7（12）：2281－2288.

［9］DUNN M G，KANG S W.Theoretical and experimental studies of reentry plasmas［R］.NASA－CR－2232，1973.

［10］GUPTA R N，YOS J M，et al.A review of reaction rates and thermodynamic and transport properties for an 11－species air model for chemical and thermal nonequilibrium calculations to 30000K［R］.NASA－RP－1232，1990.

［11］LIN T C，SPROUL L K，et al.Reentry plasma effects on electromagnetic wave propagation［R］.AIAA 95－1942.

［12］NUSCA M J，COOPER G R.Computational simulation of EM attenuation by plasmas formed in hypervelocity atmosphereic flight［R］.AIAA－98－1573，1998.

［13］董維中.熱化學非平衡效應對高超聲速流動影響的數值計算與分析［D］.［博士學位論文］.北京航空航天大學，1996.

［14］CANDLER G V，MacCORMACK R W.The computation of hypersonic ionized flows in chemical and thermal nonequilibium［R］.AIAA－88－051，1988.

［15］高鐵鎖，李椿萱，董維中，等.高超聲速電離繞流的數值模擬［J］.空氣動力學學報，2002，20（2）：184－191.

［16］YEE H C，KLOPFER G H，et al.High－resolution shock－capturing schemes for inviscid and viscous hypersonic flows［R］.NASA－TM－100097，1988.