基于環量控制無縫變彎度翼型的氣動設計

孔 博，王福新，周 濤

（1.上海交通大學 航空航天學院，上海 200240；2.中國商用飛機有限責任公司上海飛機設計研究院，上海 200232）

0 引 言

在人們提出的對下一代客機的諸多要求中，環保是最重要的主題之一，其中減少噪聲和降低污染物排放是兩個重要方面，絕大多數工程師認為，在有限時間內層流化技術是能滿足環保要求的最現實方法［1］。層流技術要求機翼表面光滑，而襟翼、縫翼的間隙會使氣流流過后馬上出現轉捩，無法繼續保持層流流動；另外，這些縫隙也是飛機起降過程中氣動噪音的主要來源之一。為了適應未來飛機發展的需要，人們探索了多種其他類型的增升系統，無縫增升就是其中具有代表性的一類。

無縫增升系統是指利用智能柔性材料，驅動機翼產生光滑連續變形，避免傳統增升裝置的驅動設備及縫道，從而實現減重、減噪、減阻的特性。因其具有無縫光滑的特點，能夠很好滿足層流機翼的要求，近年來得到了工程師們的青睞。目前得到初步應用的有A380前緣下垂裝置（Dropped Nose Device）。

本文基于MD－30P30N反構建干凈翼型，對二維翼型無縫偏轉的氣動特性進行研究，分析了前后緣弦長及偏角在無縫偏轉中對增升效果的影響。針對無縫偏轉引起的后緣大迎角氣流分離，采用主動吹氣予以改善，并對吹氣動量系數及噴口高度的影響進行研究。

1 CFD計算驗證和翼型構建

翼型繞流是粘性流體力學領域中的一類復雜流動問題，首先有必要驗證CFD計算的可靠性。MD－30P30N三段翼型是被CFD工作者廣泛采用的標模之一，如圖1所示。本文用FLUENT數值模擬30P30N翼型繞流，主控方程選為定常可壓縮流動的質量加權平均NS方程，基于密度的耦合隱式求解器求解。采用有限體積法離散控制方程，密度和對流項采用二階迎風格式，湍流模型采用SA模型。來流馬赫數為0.2，Re＝9×106，計算域為100倍弦長，利用FLUENT多重網格技術加速收斂，計算結果如圖2所示。若無特殊說明，則下文的計算條件均與標模相同。

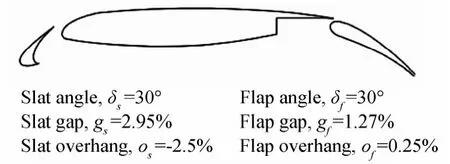
圖1 MD－30P30N三段翼型構型［2］Fig.1 MD－30P30Nmulti－element airfoil［2］

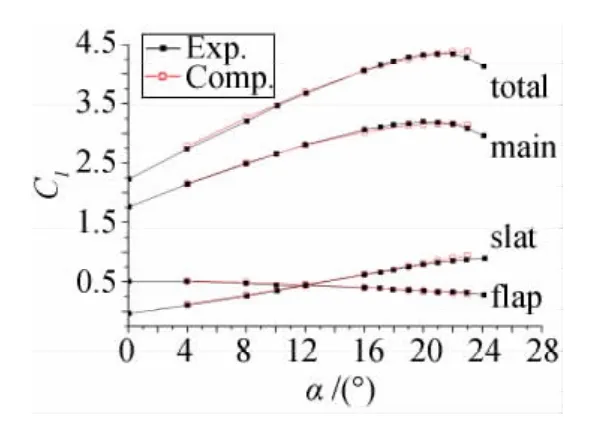
圖2 MD－30P30N翼型計算結果與實驗值對比［2］Fig.2 The simulation Clof MD－30P30N compared with experiment［2］

2 無縫變彎度翼型設計

基于MD－30P30N翼型參數，本文通過逆向設計得到一個初始干凈翼型，翼型為單位弦長，如圖3所示。其升力系數在攻角14°時達到最大，Clmax為1.716。

圖3 基于MD－30P30N構建的干凈翼型Fig.3 The clean airfoil based on MD－30P30N

后緣無縫偏轉的設計涉及變量有偏轉弦長及偏角。后緣偏轉弦長的選擇，應綜合考慮增升效率和結構等方面的因素。弦長太小，氣動效率低；弦長增加，氣動效率增加，但其長度要受到機翼后梁位置的限制（后梁的位置一般在根弦65%處）［3］，本文限定后緣偏轉比例不大于32%。鑒于傳統富勒襟翼最佳偏角約為35°～40°［3］，則設計偏角可選取20°～50°之間。同時取偏轉弦長的25%為柔性變形段，驅動機翼光滑無縫變形，柔性段用樣條線光滑連接，并保持與主翼曲率連續，其余為保形的剛性段，旋轉軸取在機翼下表面。

前緣無縫偏轉弦長同樣要受到機翼前后梁位置的限制（前梁的位置一般在根弦的15%處）［3］。傳統前緣縫翼的弦長約為當地機翼弦長的12%～16%，因此前緣偏轉弦長可取9%～15%；目前前緣襟翼的最佳偏角約為25°，前緣縫翼的最佳偏角約為20°～27°［3］，偏角過大，會因彎曲過渡段的吸力峰過高而引起氣流分離，因此前緣偏角取10°～25°。以下表面為偏轉軸，取偏轉部分弦長的1／3為柔性變形段，用光滑樣條線連接，并保證和主翼曲率連續，如圖4所示。

圖4 前后緣無縫偏轉示意圖Fig.4 Seamless deflection at leading and trailing edge

圖5是后緣偏轉弦長26%、偏角40°、前緣偏轉弦長15%、偏角25°的構型，計算得其Clmax為2.55，升力有一定的增加。但當迎角較大時，機翼尾緣出現大范圍的氣流分離，這是限制Clmax的主要因素，如果要獲得更大的升力，必須進一步采取措施予以改善。

圖5 前后緣無縫偏轉的速度場云圖Fig.5 Velocity magnitude contour of seamless deflection

3 后緣吹氣設計

環量控制技術產生高升力的機理是利用了“Coanda效應”［4］，即通過在翼型上的噴口吹氣給邊界層補充能量，推遲邊界層分離；同時，外流受高速吹氣射流的“裹挾”作用，使繞翼型流動產生很大的環量，從而獲得高升力［5］。

在后緣無縫偏轉前部添加噴口，噴管內側高度是噴口高度的4倍，噴管的長度足夠長，保證流動均勻穩定，噴口如圖6所示。如果噴口處產生超聲速流動，會在噪聲方面產生很大的負面效應，因此根據收斂噴管的臨界條件公式，保證噴口處氣流為亞聲速流動：

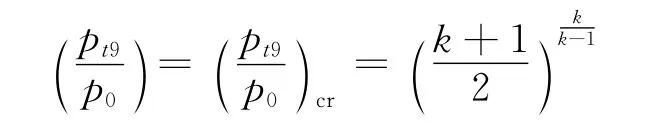
其中，p0為外壓，p9＝p0，Ma9＝1.0。噴管采用壓力入口邊界條件，根據以下公式定義邊界條件的總壓和總溫［6］：

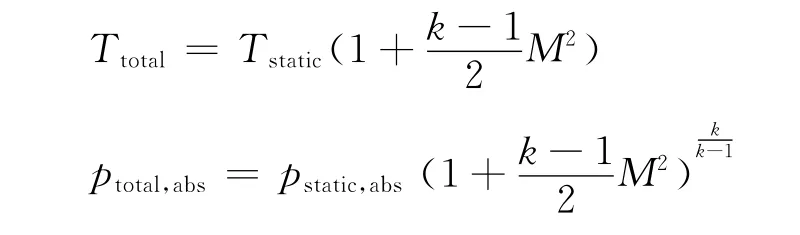
噴口高度和噴氣量是環量控制的兩個關鍵變量。參考相關環量控制文獻，噴口高度一般取機翼弦長的0.1%～0.2%［7］，本文設計范圍取0.08%～0.22%。噴氣量則用噴氣動量系數公式表示［8］：

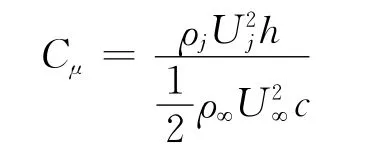
式中分子ρj和Uj分別為噴口處噴流的密度和速度，ρ∞和U∞分別為自由來流的密度和速度，h為噴口高度，c為翼型弦長。在升力曲線計算過程中，隨著攻角變化，噴口處外壓是不斷變化的，公式計算值和實際值會不同，因此需要對計算結果用后處理軟件測定噴口處空氣實際屬性值，對動量系數修正。

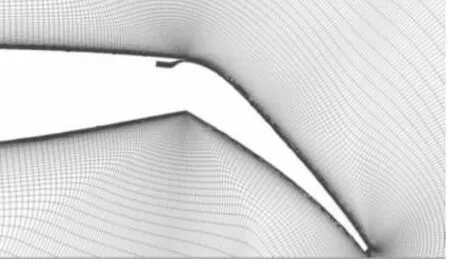
圖6 噴口設計及網格劃分示意圖Fig.6 The jet nozzle and grid

圖7是圖5所示構型在噴口1.25mm、動量系數0.053時的速度云圖，圖8中“Exp.”是和 MD－30P30N的壓力對比。可以看出，后緣吹氣氣流為邊界層補充了能量，有效改善了后緣的氣流分離，繞整個翼型的環量增加；壁面射流除了推遲邊界層分離外，還能對外流產生很強的“裹攜”作用，從而更加有效地提高翼型的升力。需要指出的是，吹氣動量系數越大，則發動機的能量損失越大，因此有必要引入參數ΔMμ＝ΔCl／Cμ加以限制，即單位動量系數帶來的升力增量。

圖7 噴口1.25mm、動量系數0.053構型的速度云圖Fig.7 Velocity magnitude contour（nozzle height 1.25mm，momentum coefficient 0.053）

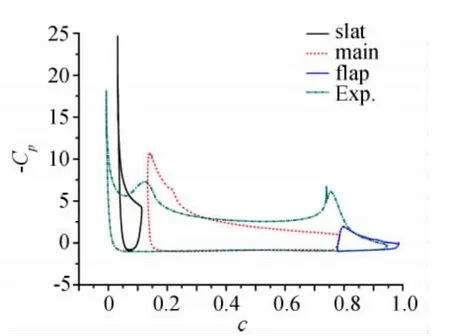
圖8 無縫構型和MD－30P30N的壓力分布比較Fig.8 Pressure distribution comparison between seamless airfoil and MD－30P30N

4 多參數整體優化

上文涉及到六個變量，其對Clmax的影響是相互耦合的，因此有必要在設計空間內進行多參數整體優化，優化設計空間見表1。

表1 設計空間各變量取值范圍Table 1 Variables range of design space

在多學科綜合優化軟件ISIGHT環境中，采用多島遺傳算法對模型進行優化求解。遺傳算法作為一種高度并行、隨機、自適應搜索算法，具有全局優化的優點，適用于處理離散、連續以及整型變量等混合變量的復雜非線性最優化問題。為了抑制早熟現象的發生，采用多島遺傳算法，這是一種偽并行遺傳算法，將每個種群分為幾個稱為“島”的子種群，在每個島上分別進行傳統遺傳算法操作，同時，在島之間周期性地選擇隨機個體進行遷移操作，達到了群體的多樣性［9］。

首先利用Latin方選取70組變量，分別計算相應的Clmax、ΔMμ，建立初始響應面。設置種群數30，島數20，遺傳代數60，雜交率0.9，變異率0.01，遷移率0.05，遷移間隔5。優化限制條件為Clmax不小于4.4。目標函數如下，并設為相同權重：

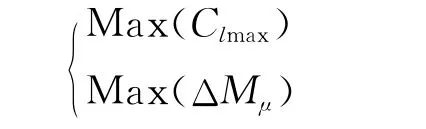
選取3組優化結果加入初始響應面中，進一步優化響應面，迭代3輪，得到優化的響應面均方根誤差Clmax為0.02151，ΔMμ為0.03908。基于優化的響應面，得到最終優化設計點為：后緣弦長30.1%、偏角38.75°、前緣弦長12.9%、偏角24°、噴口高度2.09mm、Cμ為0.089，計算得該構型下最大升力系數可以達到4.399，達到MD－30P30N多段翼型的增升水平。

5 結 論

本文對構建翼型無縫偏轉，通過改變后緣偏轉弦長、后緣偏角、前緣偏轉弦長、前緣偏角，從而改變其彎度，Clmax從1.716增加到2.5左右，但同時在大攻角下會引起后緣的大范圍氣流分離，這是限制Clmax的最主要因素。為了改善后緣氣流分離，采用環量控制方法，在后緣主動吹氣，并對噴口高度、動量系數進行研究。結果表明，后緣吹氣氣流為邊界層補充了能量，有效改善了后緣氣流分離，繞整個翼型的環量增加；此外，壁面噴流除了推遲邊界層分離外，還能對外流產生很強的“裹攜”作用，從而更加有效地提高翼型的升力。由于涉及到的六個變量對Clmax的影響相互耦合，因此需要在設計空間內進行多參數整體優化。在優化點下，該無縫變彎度翼型的Clmax達到4.399，基本達到了傳統多段翼型的水平，說明該無縫增升技術具有一定工程應用前景。

本文工作是基于二維氣動性能進行考慮，后續將其擴展到三維，從以下兩點做進一步研究：（1）吹氣動量系數與能量效率之間的關系，特別對發動機效率的影響；（2）采用大渦模擬的方法，對其噪聲性能進行評價，以確認該措施的噪聲效果。通過這些工作，將深化對無縫變彎度增升系統的理解，為增升裝置設計提供幫助。

［1］Van DAM C，PARIS J，VANDER KAM J.High－lift design methodology for subsonic civil transport aircraft［A］.Aerospace Conference Proceedings［C］.Big Sky，MT，2000.

［2］KLAUSMEYER S M，LIN J C.Comparative results from a CFD challenge over a 2Dthree－element high－lift airfoil［R］.NASA TM 887280，1997.

［3］張錫金.氣動設計［M］.飛機設計手冊第六冊.北京：航空工業出版社，2002.

［4］MCGOWAN G，GOPALARATHNAM A，JONES G S.Analytical and computational study of adaptive circulation control airfoils［A］.22nd AIAA Applied Aerodynamics Conference，Providence，RI［C］.2004.

［5］NIELSEN J，BIGGERS J.Recent progress in circulation control aerodynamics［A］.25th AIAA Aerospace Sciences Meeting［C］.Reno，NV，1987.

［6］GOLDEN R M，MARSHALL D D.Design and performance of circulation control flap systems［R］.AIAA paper，2010－1053.

［7］PFINGSTEN K C，RADESPIEL R.Experimental and numerical investigation of a circulation control airfoil［R］.AIAA Paper，2009－533.

［8］李志強，杜曼麗.Gao－Yong模型用于吹氣環量控制翼型的研究［J］.航空動力學報，2009，24（006）：1326－1331.

［9］石秀華，孟祥眾，杜向黨，等.基于多島遺傳算法的振動控制傳感器優化配置［J］.振動、測試與診斷，2008，（01）：62－65，79.