彈性系數法和回歸分析法在預測中的比較

薛佳平 張黎麗

(1.同濟大學浙江學院，浙江嘉興 314051;2.浙江嘉興環發環境科學技術有限公司，浙江嘉興 314051)

當前我國經濟處于高速發展時期，民用汽車的保有量也隨之迅速增長。機動車保有量的發展影響到環境質量、交通安全、道路建設等諸多方面。在我國，尤其是大中型城市，機動車已成為城市空氣污染的重要來源[1，2]。因此，合理預測機動車保有量是未來進行機動車污染防治規劃、道路發展規劃等的重要前提。

本文以杭州市區為例，分別采用彈性系數法和回歸分析法對民用汽車保有量的增長情況進行了預測。

1 彈性系數法預測民用汽車保有量

1.1 彈性系數法簡介

彈性系數法是在對一個因素發展變化預測的基礎上，通過彈性系數對另一個因素的發展變化作出預測的一種間接預測方法。

隨著經濟的快速發展和居民收入水平的提高，人們享受生活舒適的需求也跟著增強，私家車的大量購買，以及客貨運輸需求量的加大都導致了民用汽車保有量的增加。所以，民用汽車保有量的增長與經濟增長有著密不可分的關系[3]。本文采用國內生產總值GDP這個指標來表征經濟發展速度。民用汽車保有量增長彈性系數即為民用汽車保有量年增長率與GDP年增長率之比。

1.2 彈性系數的獲取

國內生產總值(GDP)是反映地區經濟發展的一項重要指標，其增長速率較快時，機動車保有量也隨之增長。根據杭州統計年鑒(2003年～2009年)[4]記載，杭州市區過去7年來的GDP值及其年增長率見表1，民用汽車保有量及其年增長率見表2。

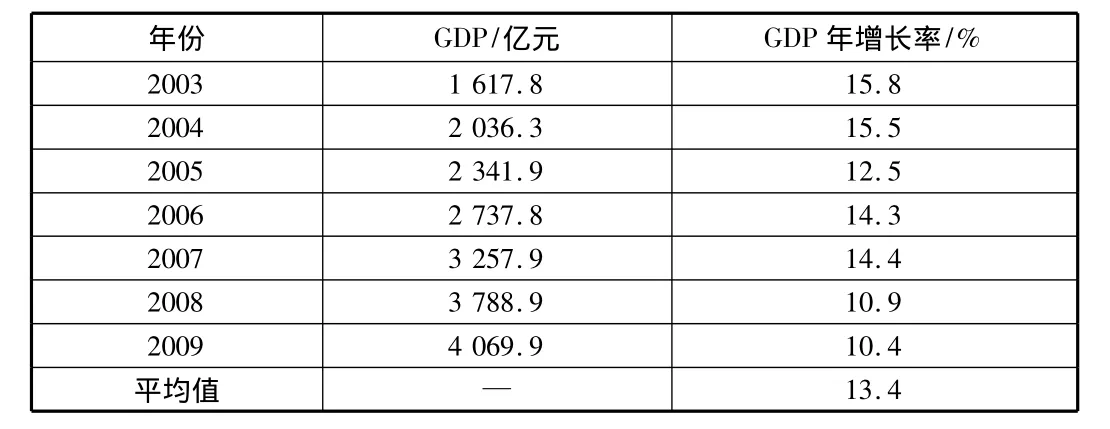
表1 2003年～2009年杭州市區GDP及其年增長率

由表1，表2得知，過去7年間，杭州市區GDP年均增長率為13.4%，民用汽車保有量年均增長率為22.3%，則彈性系數e可計算如下:彈性系數=1.67。世界各國的發展經驗表明[5]，當國民經濟處于高速發展時期，彈性系數e＞1，甚至超過2;隨著國民經濟的進一步發展，彈性系數的值下降，大都小于1。作為東南沿海城市，長三角核心區域，杭州市正處于國民經濟高速發展時期，彈性系數為1.67，符合這一規律。

表2 2003年～2009年杭州市區民用汽車保有量及其年增長率

1.3 預測模型及結果

運用下列模型對民用汽車保有量進行預測:

其中，M為預測年民用汽車保有量;M0為基準年民用汽車保有量;e為彈性系數;α為GDP年增長率，%;t為預測年;t0為基準年。

根據《杭州市國民經濟和社會發展第十二個五年規劃綱要》中的發展目標可知，杭州市在十二五規劃期間(2011年～2015年)GDP年均增長率為10%。將各數據代入式(1)中，計算得到杭州市市區2010年～2015年民用汽車保有量，見表3。

表3 彈性系數法預測結果 輛

2 回歸分析法預測民用汽車保有量

2.1 回歸分析法簡介

回歸分析，是研究變量之間的統計相關關系的一種統計方法[6]。它從自變量和因變量的一組或多組觀測數據出發，尋找一個函數式，將變量之間的統計相關關系近似的表達出來。這個能夠近似表達自變量與因變量之間關系的函數式，稱為回歸方程或者回歸函數。在回歸方程中，只有一個自變量的稱為一元回歸，有多個自變量的稱為多元回歸。由于民用汽車保有量主要與經濟發展速度有關，因此本文采用一元線性回歸分析法進行預測。

一元線性回歸法是在排除其他影響因素或者假定其他影響因素確定的情況下，分析某一因素是如何影響另一因素的過程。設自變量為x，因變量為y，則根據實驗或統計數據，可建立兩者之間的數學關系，一般為:y=ax+b。其中，a，b均為待定參數，a為回歸系數，b為回歸常數。

2.2 一元線性回歸模型的建立

經分析，地區經濟發展速度是影響該地區民用汽車保有量的主要因素，因此，本文選取民用汽車保有量為因變量，國內生產總值GDP為自變量。將表1，表2中的數據資料繪制散點圖，建立了兩者之間的一元線性回歸模型(見圖1)。

其中，y為民用汽車保有量;x為GDP值;R為相關系數。

式(2)中，R2=0.985 2，接近于1，說明民用汽車保有量變異性的98.52%能被式(2)所描述的線性關系所解釋，上述回歸模型的可靠性較強，可應用于未來民用汽車保有量增長情況的預測。

圖1 杭州市區2003年～2009年民用汽車保有量與GDP值之間的關系圖

2.3 回歸分析法預測結果

根據《杭州市國民經濟和社會發展第十二個五年規劃綱要》中的發展目標可知，2015年GDP值為10 000億元，2010年，2011年的GDP值采用統計值，將各數據代入式(2)預測2010年，2011年，2015年民用汽車保有量的增長情況，結果見表4。

表4 一元線性回歸法預測結果

3 兩種方法預測結果比較

為了對模型計算值進行驗證，采用杭州統計年鑒2010年和2011年的統計值對模型計算結果進行驗證，將兩種方法的預測值與相對誤差列于表5。

表5 模型預測值與相對誤差

從表5可以看出，彈性系數法和回歸分析法對民用汽車保有量的預測結果，相對誤差均在可接受范圍，模型預測值有一定的可信度。兩種預測模型結果均略為保守，其中，彈性系數法預測的相對誤差較小，均在－5%左右，回歸分析法預測的相對誤差較大，均在－10%左右。

4 結語

除了受經濟發展速度的影響，機動車保有量增長還與其他因素有關，如地方政策、道路承受能力、城市公共交通系統的發展等因素均影響著機動車保有量的發展。其中，政策因素影響力度較大，例如，寧波市在2004年市三區(海曙區、江東區、江北區)摩托車保有量達40 000多輛，自2005年出臺限制摩托車發展政策后，摩托車的保有量逐年下降，截止2008年，僅剩373輛[7]。所以，本文采用的彈性系數法和一元線性回歸都僅考慮了經濟發展的影響，比較適用于中短期預測。若要進行長期預測，則需考慮多方面因素，建立更為合適的模型。

[1] 廖翰博，余 志，周 斌，等.廣州市機動車尾氣排放特征研究[J].環境科學與技術，2012，35(1):134-163.

[2] 謝紹東，張遠航，唐孝炎.我國城市地區機動車污染現狀與趨勢[J].環境科學研究，2000，13(4):22-38.

[3] 李 慧，林榮娜.彈性系數法在公路工可交通量預測中的應用[J].西華大學學報(自然科學版)，2006，25(5):28-47.

[4] 杭州市統計局.2003～2009年杭州統計年鑒[Z].2011.

[5] 曹曉飛，邵春福.運用彈性系數法預測北京機動車保有量[J].道路交通與安全，2008，8(4):31-34.

[6] 韓 悅，臻孔敏.回歸分析在交通生成預測中的應用[J].山西建筑，2007，33(20):297-298.

[7] 薛佳平.寧波市機動車污染物排放清單的建立及防治對策研究[D].杭州:浙江大學，2010:14-15.