基于自動有限元建模的民機機翼結構布局優化

閆偉天 羅明強 劉 虎 武 哲

(北京航空航天大學 航空科學與工程學院，北京100191)

機翼設計是飛機總體設計中的重要組成部分，其中機翼結構設計又是機翼設計的重要內容.統計表明，每單位飛機結構重量的降低，能夠降低約4.525單位的飛機總重［1］，更低的飛機總重意味著更低的油耗，對于民用飛機意味著更強的市場競爭力，因此在滿足性能要求的前提下盡量降低結構質量就成為機翼結構優化的主要目標.由于機翼結構的布局也會對結構性能產生重要影響，因此有必要將布局優化納入到結構優化中來.

隨著CAD/CAE技術的發展，利用有限元分析技術能夠在初步設計階段快速對機翼結構進行分析，顯著提高工作效率.將有限元技術應用到機翼結構布局優化中，關鍵問題之一就是在結構布局變化，尤其是縱、橫向承力構件的數量變化后，如何實現有限元模型的自動生成［2-3］.目前的相關研究中，對上述問題都做了不同程度的簡化以降低其復雜程度，其中文獻［4-8］將橫向承力構件的布置固定，只調整縱向承力構件的位置或數量;文獻［9］中雖然考慮了縱、橫向承力構件的數量變化，但有限元模型直接以縱、橫向構件劃分單元，導致網格尺寸過大，難以保證分析結果的精度.

本文針對民用飛機中典型的雙梁式機翼結構，利用 Patran的 PCL(Patran Command Language)語言，實現了根據上、下蒙皮長桁數量和翼肋數量的變化自動進行有限元建模，并使建模精度能夠滿足初步設計的要求.然后利用Isight對Patran建模模塊和Nastran求解模塊進行集成，采用布局變量和剖面尺寸變量分離的雙層優化策略，對機翼結構布局進行了優化.

1 機翼結構自動有限元建模

在關于機翼結構自動有限元建模的研究中，一般根據機翼幾何外形和構件的位置及拓撲關系直接生成可用于有限元求解的文件.其中文獻［10］針對的是可變形飛行器的機翼建模，不能應用到常規民用飛機上;文獻［11］以機翼縱、橫向構件直接劃分有限元單元，導致單元尺寸過大，精度降低，同時該模型上、下蒙皮長桁數量必須相等，而實際工程中上蒙皮長桁數量一般多于下蒙皮長桁;文獻［12］中有限元建模需要一定的人機交互操作，并未實現完全的自動建模，無法直接集成到優化流程中.

在初步設計階段，為了實現快速迭代，對機翼進行靜強度、剛度及穩定性分析只需對機翼翼盒進行分析，一般以線、面幾何體來構建翼盒的幾何模型，然后利用桿單元、梁單元和殼單元來構建其有限元模型.本文中機翼翼盒承力構件包括前、后梁、蒙皮、長桁和翼肋，其中翼肋為順氣流方向等間距布置，蒙皮長桁為沿弦向等百分比布置.以翼根處翼肋的前緣點為原點，以平行于機身軸線向后的方向為x軸正方向，以垂直于機翼平面向上的方向為y軸正方向，建立直角坐標系來構建機翼翼盒結構的幾何模型(圖1).

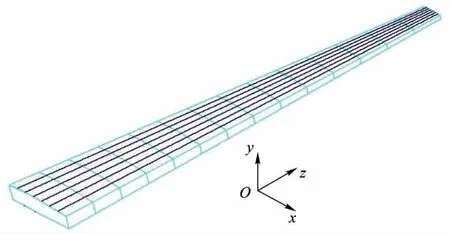
圖1 機翼翼盒整體幾何模型

下文將對機翼結構的有限元建模過程分為三步進行闡述，即分割再生成幾何體、定義局部有限元單元和生成整體有限元模型.

1.1 分割再生成幾何體

對于機翼結構的幾何模型，梁緣條和翼肋緣條分別為其腹板所在平面與上、下蒙皮曲面的交線，且梁腹板和翼肋腹板的幾何形狀由其上、下緣條決定，同時長桁也與蒙皮曲面重合.因此根據梁、翼肋和長桁將上、下蒙皮分割成若干個曲面，每個曲面本身代表該部分的蒙皮，且該曲面的邊可以描述位于該部分的翼肋緣條、梁緣條和長桁，進而由梁緣條和翼肋緣條去描述梁腹板和翼肋腹板(圖2)，這些分割生成的幾何體疊加在一起就能夠完整描述整個機翼結構.以這些幾何體的有限元單元為基礎也可以構建整個機翼的有限元模型.

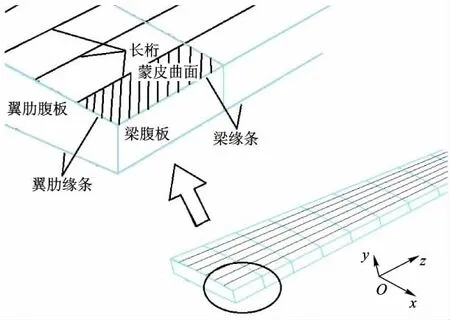
圖2 機翼構件幾何關系圖

機翼長桁、翼肋的數量發生變化后，分割生成的曲面數量也會發生變化，Patran自動執行時對幾何體的操作是通過其編號識別的，為了在操作這些曲面時不發生遺漏或錯誤，要求其編號具有一定的規律.在Patran中直接對蒙皮曲面進行分割操作，新生成的曲面編號混亂無序.而對曲線進行分割生成新曲線的編號是有規律可循的.因此本文先通過長桁對翼肋上、下緣條曲線進行分割，并根據生成曲線的展向和弦向站位對其進行編號，然后再由相鄰翼肋上弦向站位相同的緣條曲線生成曲面，再對其進行編號即可得到編號規律的曲面，且該曲面與蒙皮必然重合.梁腹板曲面可以由分割后的翼梁上、下緣條曲線生成，并根據其展向站位進行編號.

各曲線和曲面的編號原則為

其中，i為翼肋的編號，由翼根向翼梢依次遞增;j為長桁的編號，由前緣向后緣依次遞增;Nrib為翼肋的數量;Nup為上蒙皮長桁的數量;Ndown為下蒙皮長桁的數量.

為保證編號的唯一性，要求上、下蒙皮長桁數量和翼肋數量均不超過50，這是符合實際情況的.按照上述原則完成的曲線、曲面編號見圖3.

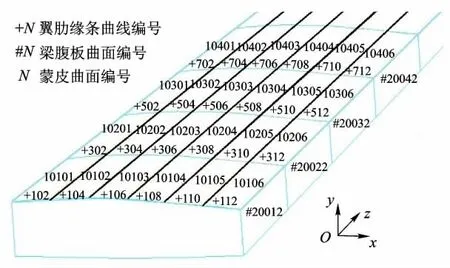
圖3 各構件的曲線、曲面編號

對于翼肋腹板，上、下蒙皮的長桁數量不同導致分割翼肋上、下緣條生成的曲線數量也不相同，因此不能通過上、下曲線生成曲面的方式構建，而是直接由未分割的上、下緣條曲線生成.

1.2 定義局部有限元單元

為了保證有限元分析結果的精度，需要對上述生成的曲面和曲線進一步劃分單元網格，然后根據單元所屬的構件定義其單元屬性.

對于蒙皮和梁腹板曲面，可以直接在其4條邊上創建網格種子“Mesh Seed”，然后將其劃分為四邊形網格“QUAD4”.通過控制種子間距一致即可保證蒙皮與腹板相交處的網格劃分一致.

對于梁緣條和長桁，與上述曲面的邊重合，可以直接對曲面的邊定義有限元單元.前面劃分曲面網格時已在邊上創建了種子，因此直接劃分曲面的邊生成的線網格與曲面網格必然一致.

為了使翼肋緣條與蒙皮曲面網格一致，通過將翼肋緣條與長桁的交點(也是蒙皮曲面的頂點)以“Associate”命令關聯到翼肋緣條上，生成硬幾何體“Hard Geometry”，然后對翼肋緣條曲線直接創建網格種子，硬幾何體處必然生成種子，控制種子間距與蒙皮曲面一致，即可保證其相交處的網格劃分一致.

對于翼肋腹板，其與蒙皮相交于翼肋緣條，與前、后梁腹板交于梁腹板曲面的邊，直接根據翼肋緣條上和梁腹板曲面的邊上的種子劃分其網格，即可保證相交處的網格一致性.

局部網格劃分完成后，各構件的網格關系見圖4.根據1.1中的編號對所有分割生成的同類型幾何體重復操作即可保證整個幾何模型被劃分了有限元網格.

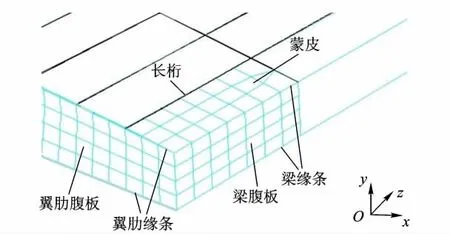
圖4 不同構件網格劃分一致

對于各構件的網格單元屬性，腹板和蒙皮單元屬性均為殼單元，長桁單元屬性均為桿單元，緣條單元屬性均為梁單元，其截面為“T”型.

1.3 生成整體有限元模型

在定義局部有限元單元的過程中，在其相交處產生了大量位置重疊的節點，為了將分散的局部有限元模型合并為一個完整的機翼結構有限元模型，可以通過合并相交處的重復節點，只保留最小編號的節點并刪除多余節點的方式實現.

對于載荷與邊界條件的定義，由于有限元單元劃分的過程中涉及了單元與幾何模型的關聯關系，在Patran中將載荷與邊界條件直接施加到幾何模型上即可保證其施加到對應的單元節點上，避免了其定義受到單元節點編號變化的影響.

最終生成的機翼結構整體有限元模型見圖5.以翼肋數為20，上、下蒙皮長桁數均為8為例，若以翼肋、長桁直接進行單元劃分，則機翼有限元模型節點數為400，單元總數為1300;而本文構建的有限元模型在網格尺寸為0.15 m時節點數為3481，單元總數為6324，精度遠高于前者.

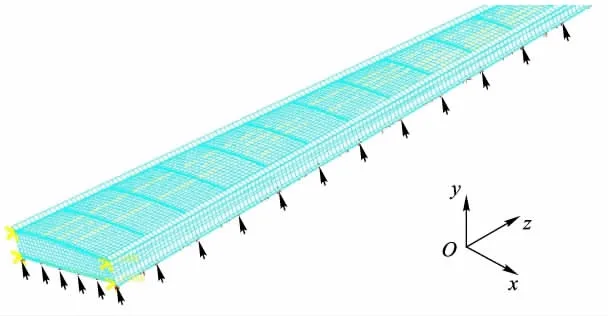
圖5 機翼翼盒整體有限元模型

2 布局優化模型和優化策略

2.1 優化數學模型

2.1.1 優化變量

優化變量包括布局變量和尺寸變量.

布局變量有3個，分別為翼肋數量xrib，上蒙皮長桁數量xstrup，下蒙皮長桁數量xstrdown.

尺寸變量有12個，分別為上、下蒙皮長桁的截面積astrup，astrdown(m2);上、下蒙皮的厚度tskinup，tskindown(m);翼梁、翼肋腹板的厚度 tsparweb，tribweb(m);翼梁上緣條的高度和厚度hsparup，tsparup(m);翼梁下緣條的高度和厚度hspardown，tspardown(m);翼肋緣條的高度和厚度hribflange，tribflange(m).其中翼梁緣條的特征參數見圖6.

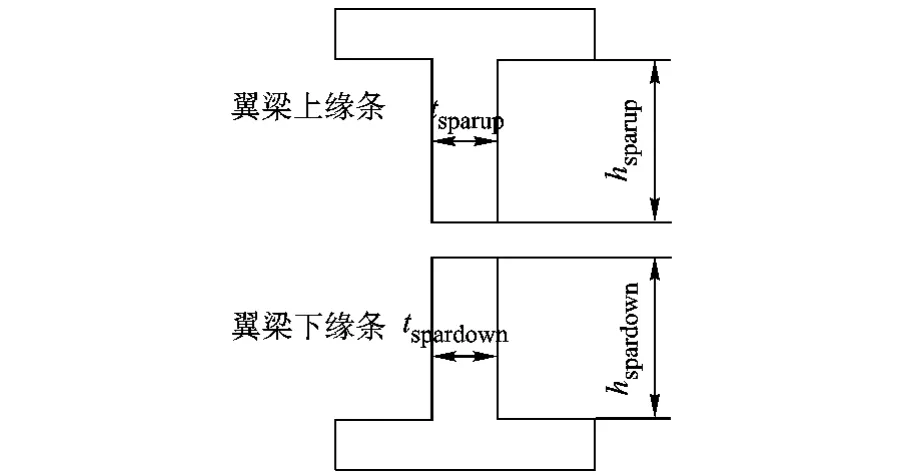
圖6 翼梁上下緣條截面特征參數

2.1.2 目標函數

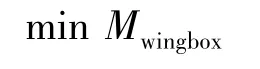
其中，Mwingbox為機翼翼盒質量(kg).

2.1.3 約束條件

其中，σb為最大正應力(MPa);［σb］為材料的抗拉強度，［σb］=450 MPa;σs為最大剪應力(MPa);［σs］為材料的抗剪強度，［σs］=250MPa;smax為機翼的最大位移，(m);lspan為機翼的半展長;e為機翼蒙皮失穩特征值.

2.2 優化策略

由于優化變量中既包括離散的設計變量(布局變量)，又包括連續的設計變量(尺寸變量)，對其同時進行優化會存在難以收斂、計算時間漫長的問題.

本文采用雙層優化的策略，上層對布局變量進行優化，在布局固定的情況下，下層對機翼結構剖面尺寸變量進行優化，得出該布局下滿足約束條件的最低質量，上層布局優化根據下層尺寸優化的結果對布局變量進行尋優，最終找到使機翼翼盒質量最低的布局即為最優布局.

上層布局優化采用多島遺傳算法(Multi-Island Genetic Algorithm)，該算法屬于遺傳算法的一種，適用于優化離散變量，并具有較強的全局尋優能力.

下層尺寸優化采用MMFD(Modified Method of Feasible Directions)算法，該算法是一種直接搜索的數值優化算法，適用于優化有約束問題，并具有快速獲得最優點和在最優點能以較高精度滿足約束條件的特點［13］.

優化流程見圖7.

3 優化算例

3.1 算例說明

為了證明自動有限元建模和優化策略的有效性，參照某大型民用飛機的機翼外形尺寸，構建了機翼翼盒的幾何 CAD模型，機翼半展長為14.2 m，根弦長6.1 m，根梢比為0.27，前緣后掠角28°，后緣后掠角13°，前梁位于弦向的15%處，后梁位于弦向的60%處，翼根處固支，機翼沿展向受到橢圓形分布的升力載荷.

機翼翼盒采用2A12高強度硬鋁合金材料，密度2780 kg/m3，彈性模量69 GPa，泊松比0.33.

有限元模型中翼盒所受外載荷包括剛體機翼產生的氣動力和翼盒結構質量引起的慣性力.

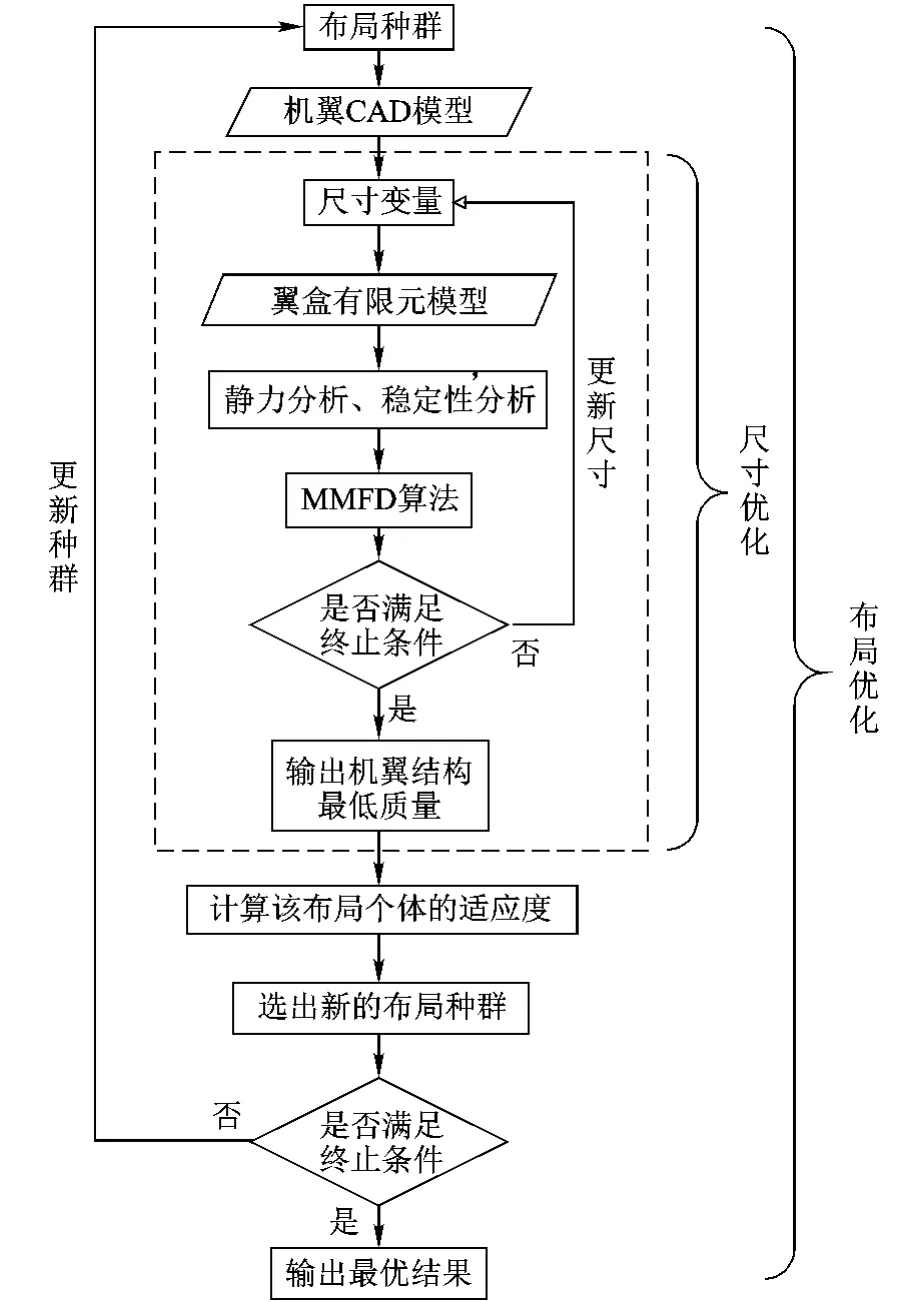
圖7 機翼布局優化流程

3.2 優化結果

機翼初始布局為翼肋數量22，上蒙皮長桁數10，下蒙皮長桁數量10，機翼結構質量3616 kg.

最終的優化結果布局為翼肋數量19，上蒙皮長桁數7，下蒙皮長桁數5，機翼結構質量3 249 kg，相對于初始布局質量降低了10.1%.布局優化迭代過程見圖8.

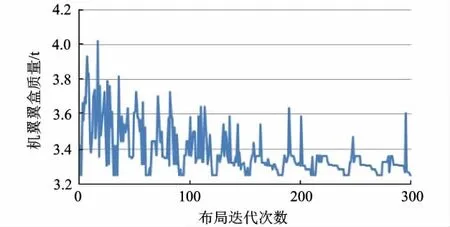
圖8 機翼翼盒結構質量的優化過程

在布局迭代過程中，每種布局下均會得到一組最優尺寸值使結構質量最低，該值隨布局迭代次數的相對變化見圖9.

對于單純的尺寸優化，結構減重主要依賴于結構件尺寸的減小和尺寸分布趨于合理，如變厚度、變截面等.由圖9可知，在布局迭代過程中，每種布局得到的最優尺寸值總體變化趨勢并不是單調減小，而是在某一范圍內波動，且本文中的有限元模型均為等厚度、等截面構件.圖8中機翼翼盒質量隨布局迭代總體呈下降趨勢，本文認為算例中的布局優化使結構減重的主要原因在于結構布局趨于合理從而減少了結構件即翼肋、長桁的數量.這也說明了結構布局的合理配置對于結構減重的重要性.

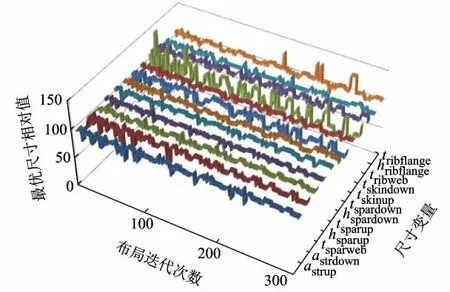
圖9 布局迭代過程中最優尺寸值的相對變化

優化前后機翼布局對比見圖10.

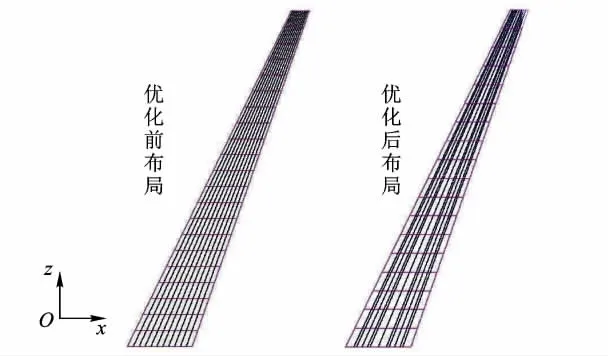
圖10 優化前后布局對比

根據最終的優化結果可知，翼肋間距約為789 mm，這與統計數據的 800 mm［14］基本一致.同時優化結果中上蒙皮長桁數要多于下蒙皮長桁數，這與實際工程經驗也是一致的.因為在彎矩載荷作用下上蒙皮受壓，增加其長桁數量可以減小長桁的間距，有利于提高其抗壓穩定性.

4 結束語

本文利用Patran的PCL語言，針對民用飛機的典型布局形式，實現了根據翼肋數量和上、下蒙皮長桁數量的變化自動進行有限元建模和分析，并將該有限元建模模塊集成到機翼結構布局優化流程中.最后的算例結果表明，優化后的布局使機翼重量得到明顯降低，且布局參數與實際工程經驗基本吻合.這說明基于自動有限元建模的機翼結構布局優化能夠為飛機初步設計工作提供一定的指導.

目前工作主要針對一種長桁和翼肋的布置形式，后續工作將增加機翼結構布局形式的種類，并通過機翼展向構件變厚度、變截面等方式進一步提高有限元建模精度.

References)

［1］ Shen J Y，Ferguson F.Weight reduction through optimal arrangement of force-carrying components within wing box structures［R］.AIAA-2004-4495，2004

［2］ Nawijn M，van Tooren M J L，Berends J P T J，et al.Automated finite element analysis in a knowledge based engineering environment［R］.AIAA-2006-947，2006

［3］王偉，常楠.飛機翼面結構多級布局優化設計思想及需要解決的問題［J］.飛機設計，2007，27(5):1-6 Wang Wei，Chang Nan.Multi-level optimization in wing structural configuration design and future research aspects［J］.Aircraft Design，2007，27(5):1-6(in Chinese)

［4］劉穎卓，張永存，劉書田，等.考慮復合材料蒙皮穩定性的飛機翼面結構布局優化設計［J］.航空學報，2010，31(10):1985-1992 Liu Yingzhuo，Zhang Yongcun，Liu Shutian，et al.Layout optimization design of wing structures with consideration of stability of composite skin［J］.Acta Aeronautica et Astronautica Sinica，2010，31(10):1985-1992(in Chinese)

［5］ Wang Wei，Yang Wei，Chang Nan.Integration shape and sizing optimization of composite wing structure based on response surface Method［J］.Transactions of Nanjing University of Aeronautics ＆ Astronautics，2008，25(2):94-100

［6］何林濤，萬小朋，趙美英，等.布局優化和尺寸優化相結合的復合材料機翼優化設計［J］.中國機械工程，2008，19(17):2077-2080 He Lintao，Wan Xiaopeng，Zhao Meiying，et al.Composite aircraft wing structure optimization using combination of layout and sizing［J］.Chinese Journal of Mechanical Engineering，2008，19(17):2077-2080(in Chinese)

［7］王偉，趙美英，常楠.基于兩相法的機翼結構幾何優化設計［J］.飛機設計，2007，27(1):22-26 Wang Wei，Zhao Meiying，Chang Nan.Geometrical optimization of aircraft wing based on double-state technology［J］.Aircraft Design，2007，27(1):22-26(in Chinese)

［8］張仲楨，余雄慶，胡添元.飛翼式飛行器結構布局與構件尺寸的兩級優化［J］.計算機輔助工程，2009，18(1):27-30 Zhang Zhongzhen，Yu Xiongqing，Hu Tianyuan.Two-level optimization on structural layout and component size of flying wing aircraft［J］.Computer Aided Engineering，2009，18(1):27-30(in Chinese)

［9］鄧揚晨，詹光，高彤，等.飛機翼面結構布局綜合設計方法研究［J］.飛機設計，2004(2):28-36 Deng Yangchen，Zhan Guang，Gao Tong，et al.Analysis and synthesis based aircraft wing structural layout study［J］.Aircraft Design，2004(2):28-36(in Chinese)

［10］ Skillen M D，Crossley W A.A matlab-based object-oriented process architecture for rapid generation of unconventional wing finite element models［R］.AIAA-2008-2160，2008

［11］羅明強，馮昊成，劉虎，等.機翼結構有限元的快速建模及自動化調整［J］.北京航空航天大學學報，2011，37(6):680-684 Luo Mingqiang，Feng Haocheng，Liu Hu，et al.Rapid wing structural finite element modeling and automated adjustment［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37(6):680-684(in Chinese)

［12］鄧揚晨，廖家駒，章怡寧，等.面向設計的飛機翼面結構有限元自動建模技術［J］.飛機設計，2002(1):9-13 Deng Yangchen，Liao Jiaju，Zhang Yining，et al.Design-oriented finite element auto-modeling to aircraft wing structures［J］.Aircraft Design，2002(1):9-13(in Chinese)

［13］ Dassault Systèmes.Isight 4.5 Component Guide［M］.USA:Dassault Systèmes，2010:621-623

［14］王寶忠.飛機設計手冊第10冊:結構設計［M］.北京:航空工業出版社，2000:410-411 Wang Baozhong.Aircraft design manual vol 10-structure design［M］.Beijing:Aviation Industry Press，2000:410-411(in Chinese)