加固雙曲拱橋時變可靠度研究

王 楠，劉 洋

（中交武漢港灣工程設計研究院有限公司，武漢 430070）

一般來說，雙曲拱橋是由多個預制構件拼裝組成，施工方便，外形美觀，經常作為公路橋梁遍布各地。但在后期的運營過程中，大多數雙曲拱橋出現構件結合面開裂的現象，目前已很少使用。對出現病害的雙曲拱橋通過修復加固措施來提高承載力，可以有效的減少經濟投入，符合社會發展的需要。依據可靠度的原理，對加固后的雙曲拱橋進行研究，既可以檢驗加固效果，又可以分析出運營后期橋梁使用情況。

我國的可靠度研究起步較晚，但發展速度很快，取得了不少結論性的研究成果。文獻［1］研究了多種腐蝕因素（混凝土碳化引起的鋼筋腐蝕、氯離子侵蝕引起的鋼筋銹蝕及硫酸鹽和硫酸溶液引起的混凝土腐蝕等）作用下混凝土構件的可靠度分析方法。文獻［2］改進了方向抽樣法，使Monte－Cole法的計算精度更高。文獻［3］運用可靠度理論，分析了既有結構的剩余壽命，對結構后期的運營有較強的指導意義，為交通運輸管理部門作出正確決定提供參考。文獻［4］將模糊數學的方法引入可靠度中，分析了CFRP 加固后的混凝土梁的可靠度指標，該研究提高了可靠度計算的精度，對實際工程具有指導意義。該文根據實測的混凝土強度值，利用時變可靠度理論，綜合考慮抗力衰退、荷載隨機變化等因素，分析了采用增大截面法加固的雙曲拱橋的可靠度及剩余使用壽命。

1 時變可靠度分析

1.1 時變可靠度的基本理論

橋梁結構的時變可靠度定義［5］：在規定的繼續使用期內，在正常使用、正常維護條件下，考慮環境和結構抗力衰減等因素的影響，在任意時刻完成預定功能的概率，即Ps（t）∈［tτ，Ts］，可用公式（1）表示。

其中

式中，tτ為橋梁結構服役分析時刻；Ts為設計基準期；Z（t）為考慮橋梁結構tτ時刻的功能函數；R（t）為考慮tτ時刻橋梁結構；S（t）為考慮tτ時橋梁結構荷載效應。

1.2 加固后結構的時變可靠度計算

隨著時間的推移，結構的使用性能不斷發生著變化，構件會出現老化和損傷現象。因此，結構的抗力計算，要綜合考慮多種因素的作用，其中，主要有荷載效應因素、使用環境因素和材料因素。其抗力衰減表達式為

式中，Kp為描述計算模式不確定性的隨機變量；R（·）為由材料參數和幾何參數計算得到的抗力隨機過程。

對于加固后的結構，可以按照一般既有結構時變可靠度分析方法得到。文獻［6－7］通過調查分析得出混凝土強度和鋼筋隨時間變化的規律。根據研究需要，文中采用文獻［10］將結構抗力的隨機過程表示為

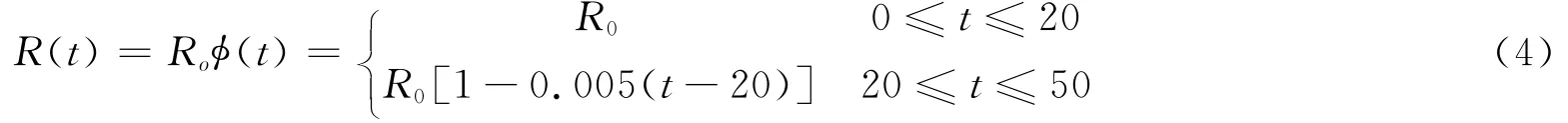
式中，R0為結構的初始抗力；（t）為一確定性的時間函數。

1.3 荷載模型

結構在運營過程中，要承受多種荷載效應，包括恒載、汽車荷載、行人荷載、風荷載和地震荷載等，若研究所有荷載作用下橋梁的內力變化對結構可靠度的影響既不科學又不實際。因此，根據該文工程實例的具體運營情況，在進行結構可靠性分析時只研究恒載和汽車荷載。

1.3.1 恒載

一般情況下，橋梁的恒載近似不變。但在橋梁運營的后期，由于各種病害的出現，需要進行維修和加固。采用增大截面法加固使原結構的截面發生了顯著變化，結構的自重變化較大，其標準值與擬建結構有較大差異，應當在對橋梁加固后的實際尺寸進行詳盡的實測統計分析后，重新求得構件自重統計參數，均值為uG＝1.104 8GD，變異系數為δG＝0.043 1。其中，GD為恒載設計值。

1.3.2 車輛荷載

橋梁加固后，在不考慮荷載等級提高的情況下，車輛荷載效應最大值分布依然服從極值I型。時段t內可變荷載效應的平均值和均方差為

式中，a＝π／（）；uQT，σQT分別為可變荷載的平均值和標準差；uQT0，σQT0分別為設計基準期T0內荷載效應極大值的平均值和標準差。

1.4 可靠度分析

1.4.1 基本假設

采用增大截面法加固混凝土構件時，一般會在老混凝土上植筋，再澆筑新混凝土，這種方法可以有效的結合新老混凝土，所以在該文的分析過程中，不考慮新老混凝土之間的變形協調問題。荷載效應主要考慮恒載和汽車荷載。

1.4.2 可靠度計算步驟

采用Midas／Civil對結構進行有限元分析，考慮抗彎失效模式。由于拱波、拱板對結構的彎矩貢獻較小，故在建模中不對該部分進行模擬，其自重以體力的形式直接施加在立柱上。

1.4.3 一次二階矩法

一次二階矩法的基本原理是：首先將隨機變量的非正態分布轉化為正態分布，然后將功能函數用泰勒級數展開。

2 工程實例

2.1 工程概況

某雙曲拱橋梁全長57m，橋面總寬8.33m，上部構造為L0＝40m 的雙曲拱，凈矢高f0＝5.71m，矢跨比f0／L0≈1／7，已服役33年。舊橋設計荷載等級為汽車－15級，掛－80。

本橋采用增大截面法加固，主要是在拱角至L0／4之間的拱背上澆筑不等厚的混凝土。在拱角處澆筑45cm 厚的混凝土，在L0／4處澆筑25cm 厚的混凝土，其間逐漸變化。新舊混凝土之間采用植筋的方法進行連接，如圖1所示。該橋加固后的設計荷載為公路－Ⅱ級。

2.2 可靠度計算

根據檢測數據（見表1），計算得到的混凝土強度值f＝10.36 MPa，建立有限元模型圖如圖2所示。計算分析表明拱腳為最不利截面，故取拱腳截面為控制截面。

考慮抗彎失效模式，計算拱腳的抗力及荷載統計參數，見表2。

橋梁在運營期間，汽車荷載效應的計算采用離散化的方法，離散時間為5年，按照式（5）、式（6）計算相應的統計參數，見表3。

表1 實測混凝土強度值

表2 抗力及荷載統計參數

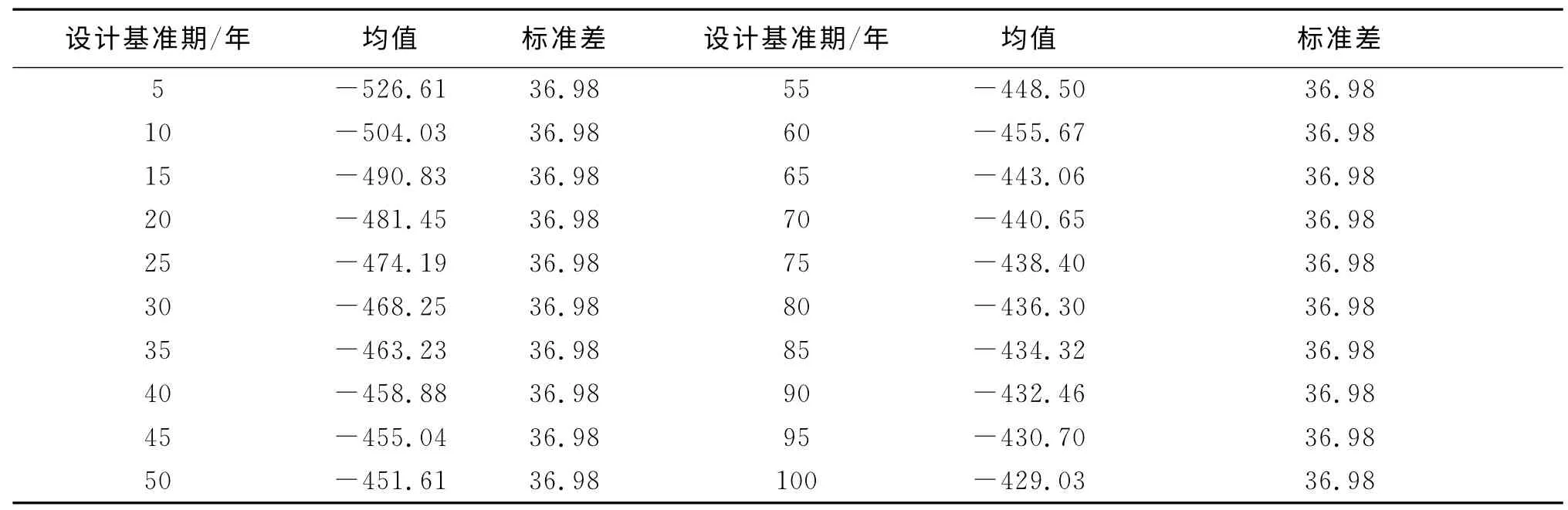
表3 車輛荷載統計參數

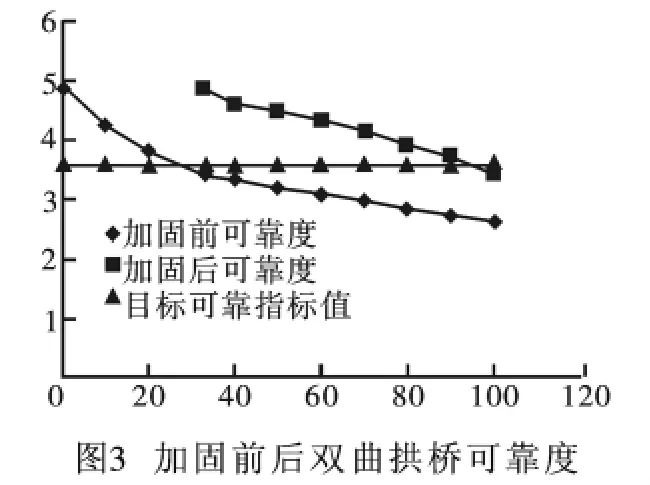
根據表3所示的各個使用階段荷載統計參數，采用一次二階矩法對構件進行可靠度計算，結果顯示加固前的雙曲拱橋可靠度指標為β＝3.52＜0.85β0＝3.57（β0 為設計基準期內的目標可靠度）。從結果可以看出，可靠度指標不滿足要求，需要進行加固。采用拱背增大截面的方法進行加固后，該雙曲拱橋的可靠度指標為β＝4.1，在后續服役60年內結構的可靠度均可以滿足使用要求（如圖3所示）。

4 結論

該文結合一拱背加固的雙曲拱橋實例，分析各因素對加固后拱橋可靠度的影響，得到結論如下：

a.采用在拱背澆筑混凝土的方法在有效提高雙曲拱橋抗力的同時，明顯提高了結構的可靠度；

b.根據目標可靠度，利用結構可靠度指標與時間的對應關系，可以得出結構剩余使用壽命，為既有結構的加固改造提供合理的決策依據。

［1］仲偉秋，趙國藩.多種腐蝕因素作用下鋼筋混泥土結構的可靠度分析［J］.土木工程學報，2001，36（11）：1－5.

［2］貢金鑫，何世欽，趙國藩.結構可靠度模擬的方向重要抽樣法［J］.計算力學學報，2003，12（6）：655－661.

［3］趙尚傳，趙國藩.基于可靠性的在役混凝土結構剩余使用壽命預測［J］.建筑科學，2001，17（5）：19－22.

［4］盧少微，謝懷勤.CFRP加固RC梁的模糊隨機可靠度數值模擬［J］.應用力學學報，2009，26（1）：161－185.

［5］彭文韜，鄧志勇.基于時變可靠的橋梁評估與剩余壽命預測.［J］武漢理工大學學報，95－97.

［6］趙尚傳，趙國藩，貢金鑫.在役混凝土結構最優剩余使用壽命預測［J］.大連理工大學學報，2002，17（5）.

［7］Mori Y，Ellingwood R.Time－dependent System Reliability Analysis Adaptive Importance Sampling［J］.Structural Safety，1993，12（1）：59－73.

［8］貢金鑫，趙國藩.大氣環境下銹蝕對鋼筋混凝土結構可靠度的影響［J］.大連理工大學學報，2000，40（2）：210－213.