破解HFEM公鑰密碼方案

古春生

(1. 江蘇理工學院 計算機工程學院，江蘇 常州 213001；2. 中國科學技術大學 計算機科學與技術學院，安徽 合肥 230027；3. 常州市云計算與智能信息處理重點實驗室，江蘇 常州 213001）

1 引言

由于計算數論上的因式分解問題、離散對數問題和橢圓曲線對數問題存在多項式時間量子算法[1,2]，因此，研究既能抵抗經典密碼分析技術，又能抵抗量子密碼分析技術的公鑰密碼方案是公鑰密碼學發展中的重要問題。目前設計抗量子計算的公鑰密碼方案成為密碼學研究的熱點之一。當前密碼學界認為能抗量子計算的公鑰密碼方案主要有基于散列問題的公鑰密碼、基于編碼問題的公鑰密碼、基于格問題的公鑰密碼、基于多變量問題的公鑰密碼等[3]。在這些公鑰密碼方案中，基于多變量的公鑰密碼因其計算速度快，密碼膨脹率低的特點而成為“后量子密碼學”研究的重要方向。近年來，設計構造基于遍歷矩陣性質的密碼原語已經引起了研究人員的廣泛關注[4～9]。文獻[4～6,8]研究了GF(2k)上的遍歷矩陣性質，并給出了其在加密數據、生成偽隨機數、生成信息摘要、Shamir三次傳遞協議等密碼學上的應用，文獻[10～12]利用遍歷矩陣研究了公鑰密碼協議的半群作用問題。文獻[13]構造了基于有限域上遍歷矩陣的雙側冪乘問題的公鑰加密方案。文獻[14]基于BMQ問題(bisection multivariate quadratic equation problem)的困難性提出了隱藏域上遍歷矩陣的公鑰密碼方案。盡管文獻[14]證明了有限域上BMQ問題是NP完全，但并沒有證明基于隱藏域上公鑰密碼方案的安全性。本文主要構造破解文獻[14]中 HFEM(hidden field ergodic matrices)公鑰密碼方案的多項式時間算法。

本文多項式時間破解算法非常簡單，即根據文獻[14]的方案公鑰中隱藏的遍歷矩陣性質求出一個等價私鑰，然后利用這個私鑰對密文直接解密。具體說即通過分析發現文獻[14]的公鑰矩陣具有形式WB1, WB2，并且W可逆，矩陣 B1、 B2屬于同一個遍歷矩陣E的生成集，即，因而能夠計算出矩陣根據遍歷矩陣性質，矩陣 B0屬于遍歷矩陣E的生成集。然后，本文利用 B0依次求出 HFEM公鑰密碼方案的一個等價私鑰。

2 趙永哲等人的HFEM公鑰密碼方案

為完整性，本節自適應地引用文獻[14]中相關問題的定義和基于HFEM的公鑰密碼方案。

q遍歷矩陣生成元，記

定義 1 BMQ-問題：S為 Fq上有m個方程和2n個變量的方程組，其每個方程形式可表示為

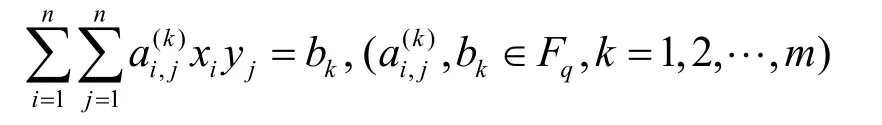
為易于證明，筆者自適應地引用文獻[14]中基于HFEM的公鑰密碼方案如下。

密鑰生成如下。

1) 隨機選擇矩陣集(A, B)。這里 A = { A1,… ,，要求滿足A線性無關，且B是遍歷矩陣E生成矩陣集 Fq[ E ]的基；

2) 隨機選擇變換矩陣 R ∈ GL2n( Fq)，并計算

3) 由RAB生成2n個BMQ多項式：[ρ1( x , y),…,

加密算法如下。

解密算法如下。

1) 給定私鑰sk和密文C，計算 T = ( R-1×C)

2) 給定私鑰sk和T，解出方程組 E ( A, B,T )的

3) 根據(x, y)與(α, β)等價，計算輸出明文P=x? y = α ? β 。

根據文獻[14]，方程組 E ( A, B ,T )定義為：這里定義，注意等式左邊符號系符號混用，僅表示矩陣符號，目的是與文獻[14]中原文一致，并不表示矩陣 A , B相乘后再將AB的元素按行排列后所對應列向量。在已知(A, B)的情況下，方程組 E ( A, B ,T )易于求解。

3 破解HFEM公鑰密碼方案

盡管文獻[14]證明了BMQ問題是NP難的(定理1)，但文獻[14]并沒有歸約HFEM公鑰密碼方案的安全性到求解BMQ問題。通過分析上述HFEM公鑰密碼方案，筆者知道破解公鑰方案的關鍵是求出 VS(B)的一個基。為此，首先給出與遍歷矩陣相關的2個引理。

證明 因 f (λ)=|λ I-E|，故f(λ)為次數為n的多項式。用反證法，假定 f (λ)是可約的，則 f (λ)或者是不可約多項式的冪，或者可以表示成2個互素多項式的積。下面分別證明它們是矛盾的。

1) f(λ)可表示成2個互素多項式的乘積。

不失一般性，設 f ( λ) = g1( λ)g2(λ)，deg(g1(λ))=k，1≤k＜n，deg(g2(λ))=n - k 和 g cd(g1(λ),g2(λ) ) = 1。

因E為遍歷矩陣，故 f(0)=|E |≠0，所以g1(0) ≠ 0,g2(0) ≠ 0。

由deg(g1(λ))=k和g1(0)≠0，可知剩余類環Fq[λ]/(g1)只包含qk-1個非零元素，所以剩余類集合{λi|i = 0,… ,qk-1}中存在2個非零元素λr, λs滿足 λr≡ λsm od g1(λ)，即存在正整數 0 ＜e1≤qk-1滿足 λe1≡1mod g1(λ)。

同理可證存在正整數 0 ＜e ≤qn-k-1，滿足2λe2≡1mod g2(λ)。

由gcd(g1( λ),g2(λ)) = 1，得并且 0 ＜ e e ＜ qn-1。12

因|Fq[ E ] |= qn-1和 f (λ)為遍歷矩陣E的特征多項式，故滿足 λe≡1modf(λ)的最小正整數是e = qn-1。

所以 ( qn- 1 )|(e1e2)，矛盾。

2)f(λ)是不可約多項式的冪，即f(λ)=g(λ)r,r≥ 2 。因 g (λ)為不可約多項式，且 g ( 0) ≠ 0 ，則e = qn/r-1是滿足 λe≡1modg(λ)的最小正整數。故f(λ) = g(λ)r|(λqn/r-1- 1 )r。

因 Fq為有限域，故 Fq中元素個數一定是某個素數的冪。設素數p是 Fq的特征，則 Fq有 pk個元素，這里k是 Fq在素域 Fp的擴張次數。設v是滿足pv≥r的最小正整數。因為，則

又因 e = qn-1是滿足 λe≡1modf(λ)的最小正整數，所以 ( qn-1)|( pv( qn/r- 1 ))。因λ≥2，矛盾。

根據遍歷矩陣特征多項式的不可約性可以得到有限域 Fq上模 f (λ)的多項式 Fq[λ]產生多項式的有限域，與遍歷矩陣同構。

引理2 假定E為遍歷矩陣且|Fq[ E ] |= qn-1，f(λ)為E的特征多項式，則矩陣集 B ={E0,E1,… ,En-1}為遍歷矩陣集 Fq[E]的基。

證明 由引理1知， f(λ)為次數n的不可約多項式，因此，剩余類環 Fq[λ]/(f)中任意元素對應次數小于n的多項式 r(λ)，即又因Ek與有限域 F上次數小于n的 r (λ) = λkm od f(λ)

q一一對應，即在有限域Fq上矩陣 Ek等于 r(E)。而r(E )中所有E的次數小于n，即 Fq[E]中任意元素可以用B表示。同理可以證明，由B生成的元素也屬于 Fq[E]∪ { 0}。

因 f (λ)為E的不可約特征多項式，故 f (E)為關于矩陣E滿足 g ( E ) =0的多項式中最小次數的多項式。故矩陣集B線性無關。因此，B是 Fq[E]的基。

q個基。

因為 R ∈ GL2n( Fq)，A線性無關，由文獻[15]可知：

rank(R) + r ank(A) - 2 n ≤ ra nk(R A) ≤ min(rank(R),rank(A) ) 。

因此，rank(RA)=n。不失一般性，設W1∈GLn( Fq)，即在有限域 Fq上 W1可逆。

又因為 B1∈GLn( Fq)，知W1B1可逆。故可以計算因此，可以計算得到和根據定理1可知 B '是 Fq[E]的基。

顯然，易于證明上述求解 B ', A'算法所需時間是多項式時間算法。因為使用高斯消元法計算 B1的逆矩陣需要時間為 O ( n3)；計算 B '中矩陣乘積Bi，i=2,…, n 需要時間為(n-1)× O ( n3)= O ( n4)；計算 A '需要時間為2× O ( n3)= O ( n3)。這里假定 Fq上任意一次算術運算需要時間為1個單位時間。

證明 根據定理 2，可以在多項式時間內求解B', A'，且 B '也是 Fq[E]的基。

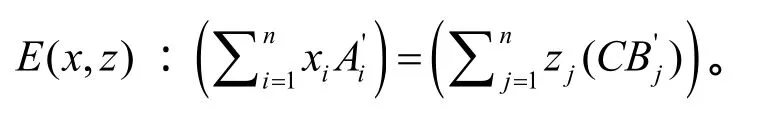
3)求解該方程組 E ( x, z)得一組非零解(x, z)

元法求逆得b。

6) 由(x, y)求出 E ( A', B ', C)的全部(q - 1 )個相互等價的解

7) 根據 HFEM 公鑰密碼方案，計算輸出明文P = x ? y 。

4 破解HFEM公鑰密碼方案舉例(n=3，q=5)

本節通過實例演示破解HFEM公鑰算法。首先生成 HFEM公鑰；然后根據公鑰求解基 B '和A'；最后根據 HFEM公鑰密碼方案對密文進行解密。

4.1 生成HFEM公鑰

根據定理1可知，選擇B只要為 Fq[ E ]的基即可，易于驗證上述選擇的B符合條件。計算輸出公鑰為

4.2 求解基 'B和 'A

現根據定理 2，使用公鑰RAB計算 Fq[ E]的基B'和 A '如下。

2)計算13W B逆

4.3 加密算法

給定公鑰RAB，設明文為 P =α?β=（4 2 3）?（2 3 1）。計算密文如下

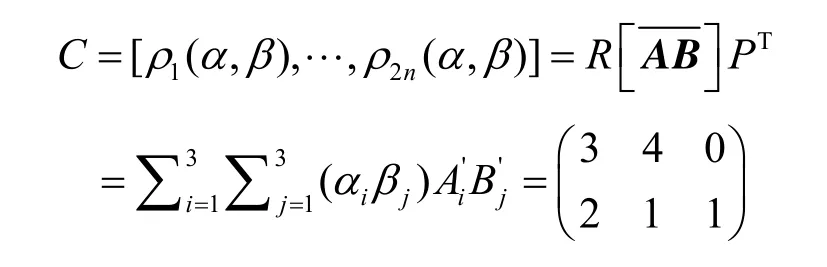
4.4 解密算法

1) 根據文獻[14]和求解的基 B '和 A '可列方程組 E ( A', B',C)

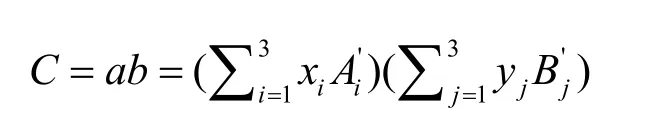
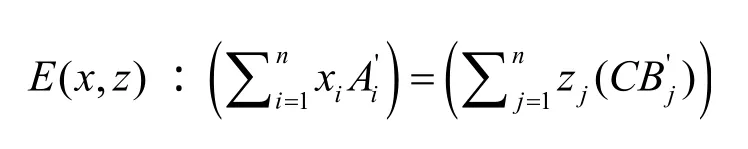
3) 求解該方程組E( x, z)得一組非零解x=（3 4 1）,z= （ 1 0 2） 。

6) 輸出明文 P ' = x ? y 。易于驗證明文 P = P '。

5 結束語

利用遍歷矩陣的性質，本文給出從HFEM公鑰密碼方案的公鑰直接求解其等價私鑰的多項式時間算法，從而破解了文獻[14]設計的HFEM公鑰密碼方案。最后，通過計算示例演示HFEM公鑰密碼方案的破解過程。

[1] SHOR P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM Journal on Computing, 1997, 26(5)：1484-1509.

[2] PROOS J, ZALKA C. Shor's discrete logarithm quantum algorithm for elliptic curves[J]. Quantum Information and Computation, 2003,3(4)：317-344.

[3] BUCHMANN J, DING J T. Post-quantum cryptography[A]. The Second International Workshop, PQCrypto 2008[C]. Cincinnati, USA, 17-19.

[4] 趙永哲, 黃聲烈, 姜占華. GF(2k)上的遍歷矩陣及其特性分析[J].小型微型計算機系統, 2005, 26 (12)：2135-2139.ZHAO Y Z, HUANG S L, JIANG Z H. Ergodic matrix over GF (2k)and its properties[J]. Mini-micro Systems, 2005, 26 (12)：2135-2139.

[5] ZHAO Y Z, WANG L O, ZHANG W. Information-exchange using the ergodic matrices in GF(2)[A]. 2nd International Conference, ACNS 2004[C]. Amsterdam： Icisa Press, 2004. 388-397.

[6] 趙永哲, 裴士輝, 王洪軍等. 利用有限域上的遍歷矩陣構造動態加密器[J]. 小型微型計算機系統, 2007, 28 (11)： 2010-2014.ZHAO Y Z, PEI S H, WANG H J, et al. Using the ergodic matrices over finite field to construct the dynamic encryptor[J]. Mini-Micro Systems, 2007, 28 (11)：2010-2014.

[7] PEI S H, ZHAO H W, ZHAO Y Z. Public key cryptography based on ergodic matrices over finite field[J]. Wuhan University Journal of Natural Sciences, 2006, 11(6)：1525-1528.

[8] 趙永哲，姜占華，黃聲烈. 基于F2上遍歷矩陣的Shamir三次傳遞協議的實現[J]. 小型微型計算機系統, 2006, 27(6)：986-991.ZHAO Y Z, JIANG Z H, HUANG S L. Implementation of Shamir’s three pass protocol based on ergodic matrix over finite field[J]. Mini-Micro Systems, 2006, 27(6)：986-991.

[9] 孫永雄，趙永哲, 楊永健等. 基于遍歷矩陣的單向(陷門)函數的構造方案[J]. 吉林大學學報： 信息科學版, 2006, 24(5)：555-560.SUN Y X, ZHAO Y Z, YANG Y J, et al. Scheme to construct one-way (trapdoor) functions based on ergodic matrices[J]. Journal of Jilin University： Information Science Edition, 2006, 24(5)：555-560.

[10] MONICO C. Semirings and Semigroup Actions in Public-Key Cryptography[D]. Notre Dame： University of Notre Dame, 2002.

[11] MAZE G. Algebraic Methods for Constructing One-Way Trapdoor Functions[D]. Notre Dame： University of Notre Dame, 2003.

[12] 黃華偉.半群作用問題在密碼學中的應用[D]. 西安： 西安電子科技大學, 2008.HUANG H W. Cryptographic Applications of Semigroup Action Problem[D]. Xi’an： Xidian University, 2008.

[13] 裴士輝,趙永哲,趙宏偉. 基于遍歷矩陣的公鑰加密方案[J]. 電子學報, 2010, 38(8)：1908-1913.PEI S H, ZHAO Y Z, ZHAO H W. Public key encryption scheme based on the ergodic matrices[J]. Chinese Journal of Electronics, 2010,38(8)：1908-1913.

[14] 趙永哲,趙博,裴士輝等. HFEM 公鑰密碼方案的設計與實現[J]. 通信學報,2011,32(6)：24-31.ZHAO Y Z, ZHAO B, PEI S H, et al. Design and implement on the HFEM public key scheme[J]. Journal on Communications, 2011,32(6)：24-31.

[15] HORN R A, JOHNSON C R. Matrix Analysis[M]. Cambridge University Press, 2005.