FSK-DWDM四波混頻的研究

張 鑫， 杜建新， 楊 輝

（南京郵電大學 光電工程學院，江蘇 南京 210046）

0 引言

頻移鍵控（FSK）憑借其高接收機靈敏度、對光纖的非線性有很高的容忍度、易解調、及其應用于光標記交換中在光載波頻段加入或提取標簽信息而不影響傳輸光強度等方面表現(xiàn)出來的優(yōu)勢，成為近年來光傳輸技術的研究熱點[1-3]。目前已有理論研究表明在單信道10 Gb/s的傳輸系統(tǒng)中，F(xiàn)SK調制與差分相移鍵控(DPSK)調制具有相當的靈敏度，并且在實驗條件下已經實現(xiàn)了在50 km的常規(guī)單模光纖（SMF）中得到速率為40 Gb/s，功率代價為0.8 dB的FSK信號[4]。隨著密集波分復用(DWDM)技術的發(fā)展[5]，光纖的非線性效應特別是四波混頻對其影響越來越大[6]。基于強度調制(OOK)調制格式，信道為非簡并，入射波為矩形脈沖波并且考慮到DWDM系統(tǒng)中的比特序列的隨機性、信道間脈沖走離效應等因素的影響情況下的四波混頻效應已被研究[7]，運用類似的方法對調制格式為FSK，入射脈沖為啁啾高斯脈沖的情況進行討論，考慮到多個信道對探測信道的影響，實例計算表明調制偏移頻率與四波混頻標準差的關系曲線圖并不是簡單的遞增遞減關系，而是當調制偏移頻率取一定的值時，四波混頻標準差有極小值，也就是最優(yōu)值。特征寬度值的大小基本不會影響到這一曲線關系，但是較小的特征寬度值能得到較小的四波混頻效應，然而群速度色散對這一曲線關系影響較大，其絕對值取很小的情況下，這一曲線基本呈線性遞增關系，隨著絕對值的增大，曲線呈震蕩變化。

1 理論計算模型

FSK調制格式下光波電場表示如下：

式中，Pimax為脈沖峰值功率，f0為信道中心頻率，Δf為調制偏移頻率[8]，T0為比特寬度，V+，V_為脈沖群速度，τr為信道r內的隨即序列相對參考信道的初始時延。

當比特信息為“1”時，比特序號為n的峰值功率歸一化的啁啾高斯脈沖在入射點的光波的電場的復振幅可以表示為：

式中，C為初始啁啾參量。

考慮到群速度色散效應：

式中，β2表示群速度色散[9]。

假設未調制載波的中心角頻率為ω0。當中心角頻率由于調制變?yōu)棣?＋Δω時，對應的信號為比特“1”，反之，當中心角頻率由于調制變?yōu)棣?－Δω時，對應的信號為比特“0”。

由于非簡并四波混頻效應產生的光場對比特“1”產生干擾對應的信道組合分以下3種情況：

在以下討論中，公式中凡是出現(xiàn)A，B，C的分別對應上面3種情況。

3種情況下的四波混頻噪聲光電流：

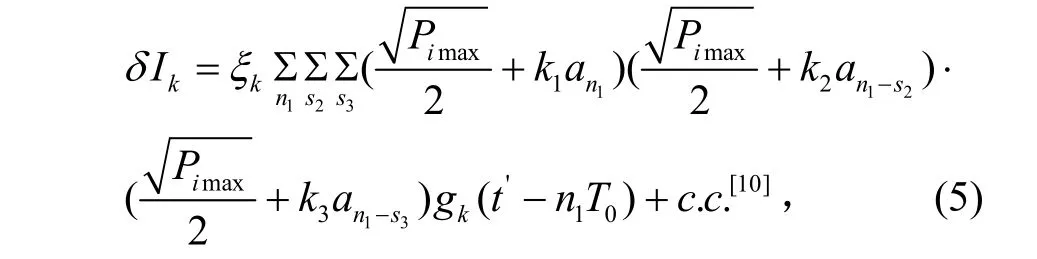
式中，k取 A，B，C，當 k=A時，k1=k2=k3=1，當k=B時，k1=1，k2=k3=-1，當 k=C時，k1=1，k2=k3=-1。

以ω1信道為探測信道：

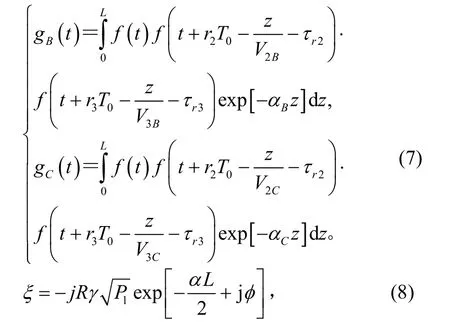
式中，R為響應度，α為光纖的損耗系數，重疊函數g(t)的計算方法類似于參考文獻[7]。

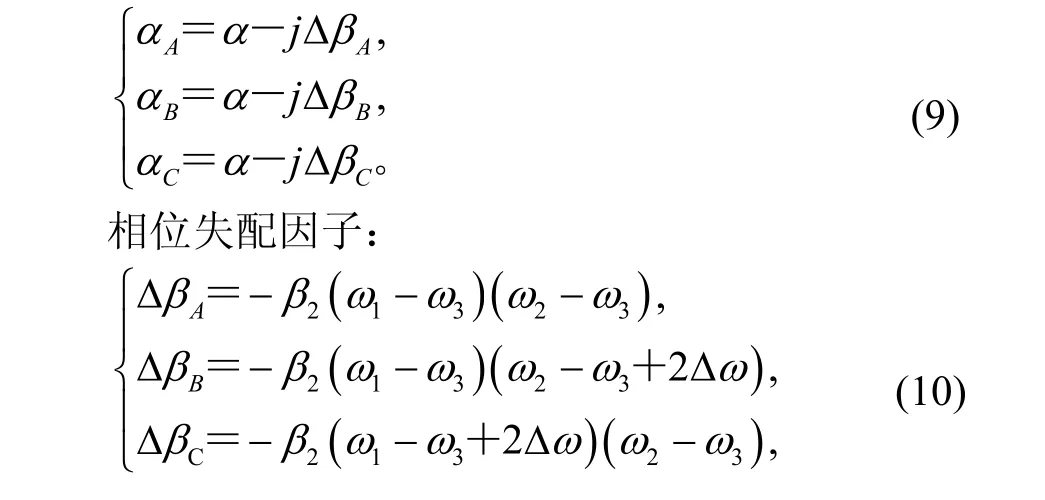
群速度的倒數表達式為：

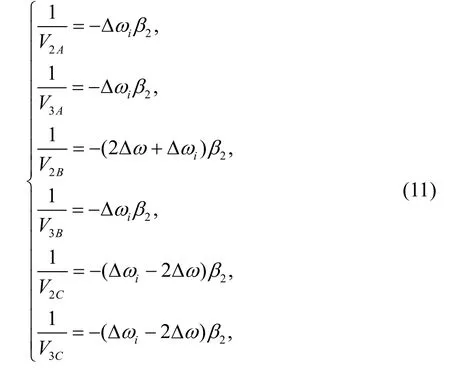
式中，Δωi為各信道間的角頻率間隔。

考慮到相關變量的隨機性，可得：

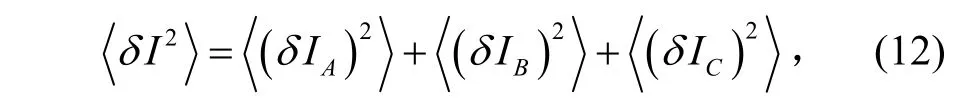
即四波混頻效率滿足：

噪聲光電流δI( t)的均方值為一個時間變量，其表達式為：

2 仿真結果及討論

設定 pimax=5 mw ,非線性系數γ=4.86 W-1km-1,以分貝作為單位的光纖損耗系數為0.217 dB/km，光波傳輸距離L=50 km ，單信道的速率為10 Gb/s，中心信道頻率 fso=190.90 THz，3個信道的啁啾高斯脈沖的初始啁啾統(tǒng)一設為 0，系統(tǒng)相鄰信道的信道間隔為100 GHz。考慮17個信道對中心信道的影響，以上參數在討論中保持不變。

圖1的參數設置為：群速度色散β2=-22ps/km，特征寬度T0=20 ps。從圖1中可以發(fā)現(xiàn)四波混頻標準差并不是遞增遞減的曲線，而是在30 GHz左右的地方有一個極小值。考慮到調制偏移頻率越大解調越方便的因素可以認為調制偏移頻率取 30 GHz左右時是比較合適的。

圖2的參數設置為：群速度色散β2=-22ps/km,特征寬度T0取了3個不同的值分別為40 ps，60 ps，80 ps，這3個值分別對應的是三角形，星形，圓形標志的曲線。從圖2中可以發(fā)現(xiàn)T0的不同并沒有影響到圖1中的最佳調制偏移頻率值，但是特征寬度T0的大小是與四波混頻標準差的大小呈正比的關系，為了減小四波混頻的影響盡量的取較小一些的特征寬度值比較合適。

圖3的參數設置：特征寬度T0=20 ps，群速度色散β2取了3個不同的值分別為-12ps/km，-5 ps2/km，-9 ps2/km，這3個值分別對應的是三角形，星形，圓形標志的曲線。從圖3中發(fā)現(xiàn)群速度色散值對調制偏移頻率與四波混頻標準差的關系曲線有較大的影響，群速度色散取-12ps/km時，曲線基本呈現(xiàn)線性遞增關系。而群速度色散取-52ps/km,-92ps/km時，曲線就呈現(xiàn)了起伏變化。

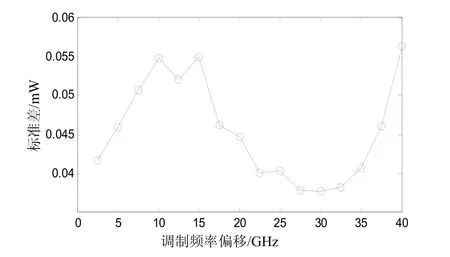
圖1 β2=-2 ps2/km，T0=20 ps情況下四波混頻標準差與調制偏移頻率的關系

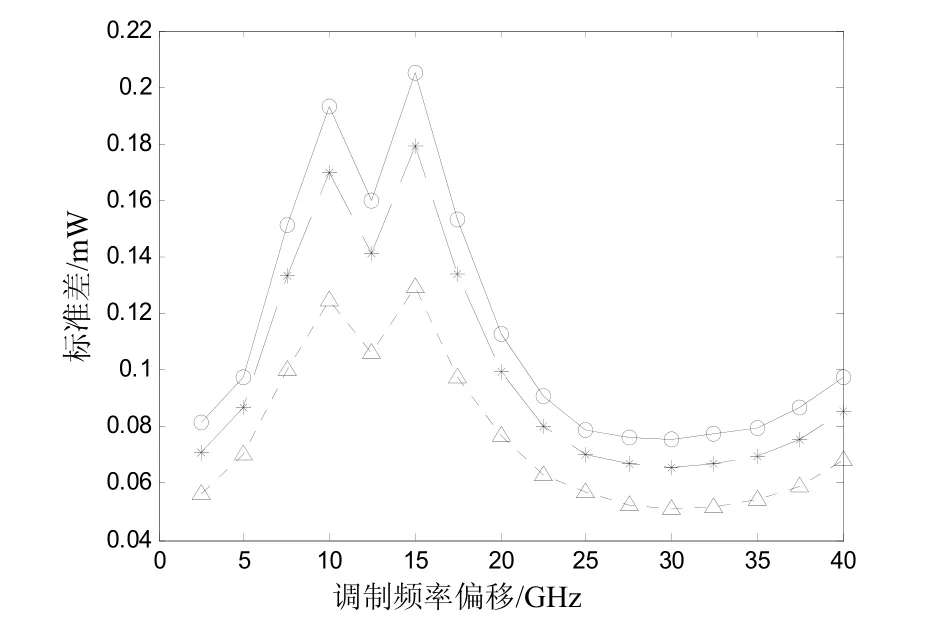
圖2 T0取不同值，β2=-2 ps2/km情況下四波混頻標準差與調制偏移頻率的關系

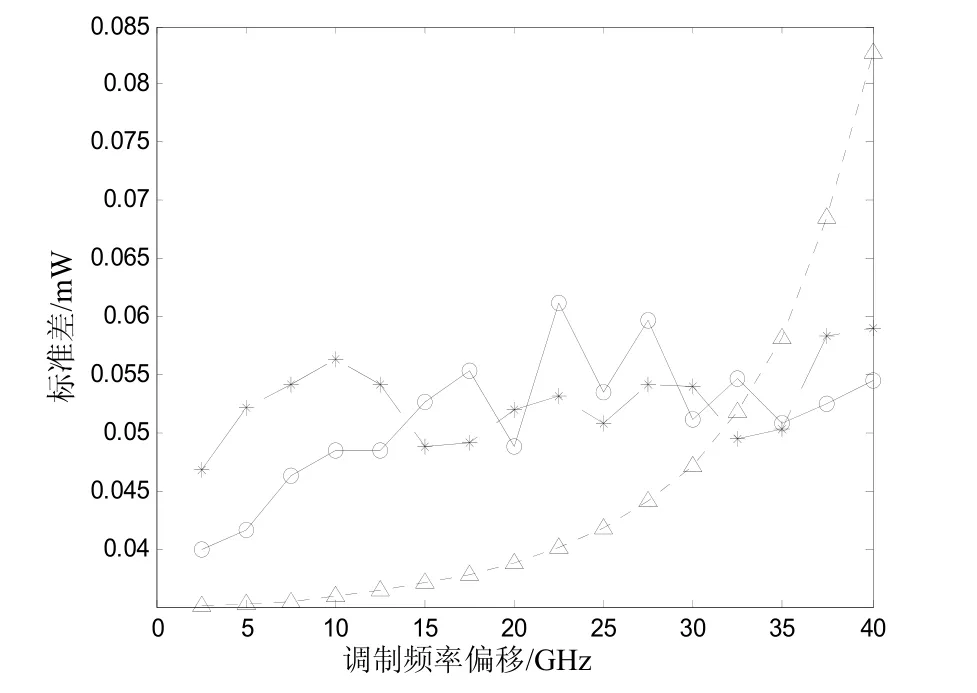
圖3 β2取不同值，T0=20 ps情況下四波混頻標準差與調制偏移頻率的關系

3 結語

考慮到DWDM系統(tǒng)中的比特序列的隨機性、信道間脈沖走離效應等因素的影響。給出了調制格式為 FSK，信道為非簡并，入射脈沖為啁啾高斯脈沖波情況下的四波混頻噪聲標準差的理論計算模型。在考慮到多個信道對于探測信道的影響的情況下用實例對其進行分析。研究結果表明在討論調制偏移頻率域四波混頻噪聲標準差的關系中發(fā)現(xiàn)它們并不是簡單的遞增遞減關系，而是當調制偏移頻率取一定的值時，四波混頻標準差有極小值，此時的調制偏移頻率為最優(yōu)取值，特征寬度值不會影響到最優(yōu)值的選取但是較小的T0值可以得到比較小的四波混頻效應。然而群速度色散對調制偏移頻率與四波混頻標準差曲線關系影響較大，其絕對值取很小的情況下，這一曲線基本呈線性遞增關系，隨著絕對值的增大，曲線呈震蕩變化。因此在具體的模型選取中需要綜合考慮這些因素。

[1]何舟.高速光通信系統(tǒng)中先進調制格式研究[D].湖北:華中科技大學,2011.

[2]李明浩.先進調制格式的產生及其全光信號處理[D].湖北:華中科技大學,2006.

[3]楊桂林,電力線載波通信接口電路的設計[J].通信技術,2010,43(05):77-81.

[4]CHI Nan,YU Siyuan.Transmission Properties of a 40 Gb/s Signal in FSK Modulation Format[J].ECOC 2005 Proceedings,2005,114(03):729-730.

[5]劉佳,黃宏光.DWDM技術及其在城域網中的應用[J].通信技術,2009,42(02):18-20.

[6]沈建華,邵鐘浩.四波混頻對 DWDM系統(tǒng)的影響[J].光纖與電纜及其應用技術,2001(04):6-9.

[7]DU Jianxin.Analysis of Non-degenerate Four-wavemixing Crosstalk in DWDM System[J].Acta Physica Sinica,2009, 58(02): 1046-1052.

[8]INOUE K,NAKANISHI K,ODA K,et al.Crosstalk and Power Penalty Due to Fiber Four-Wave Mixing in Multichannel Transmissions[J]. Journal of Lightwave Technology,1994,12(08):1423-1439.

[9]DU Jianxin.Calculation of Degenerate Four-wavemixing Noise for Chirped Gaussian Pulse in DWDM System[J].Chinese Journal of Quantum Electronics,2009,26(06):1007-5461.

[10]KUMAR S.Analysis of Degenerate Four-Wave-Mixing Noise in Return-to-Zero Optical Transmission Systems Including Walk-off[J].Journal of Lightwave Technology,2005,23(01):310-320.