色散管理WDM系統中簡并FWM噪聲的研究

楊 輝， 杜建新， 張 鑫

（南京郵電大學 光電工程學院，江蘇 南京 210046）

0 引言

隨著波分復用系統（WDM）的發展，脈沖間的非線性效應特別是四波混頻（FWM）已成為限制WDM傳輸系統性能的主要因素。FWM是一種重要的非線性效應，對于等間隔的WDM系統由FWM產生的新的光場和探測信道的頻率一致時，就會對探測信道產生串擾[1-3]，故分析四FWM對WDM系統性能影響程度，對優化系統性能有著重要意義。在分析時必須考慮到各種隨機因素的影響[4]；基于傳輸光波為連續波的情況，Inoue等人考慮到比特流及脈沖初始相位的隨機性，給出了強度調制／直接檢測(IM／DD)及頻移鍵控／直接檢測(FSK／DD)FWM功率代價的計算，并發現在較小的功率代價情況下，FWM噪聲的分布近似高斯型[5]。對于矩形脈沖波，Kumar利用頻譜分析理論，考慮到信道間脈沖走離效應，給出了簡并情況下的FWM噪聲標準差的半解析理論計算模型[6]。當前對于傳輸波為啁啾高斯脈沖波的情況有了充分的研究[7]，但其所分析的系統為無集總放大的光纖鏈路系統。Wu等人分析了傳輸波為連續波的集總放大及色散補償光纖鏈路中的FWM噪聲，并用信噪比大小進行了量化[8]。色散管理技術是現代光網絡中實現波分復用系統長距離傳輸的一項關鍵技術。基于色散管理技術的光纖鏈路中的各種非線性效應的研究，已經取得了一定的成果[9-10]，但缺少基于入射波為啁啾高斯脈沖時，色散管理光纖鏈路中FWM的研究。

理論計算模型的建立是基于已有 FWM噪聲標準差模型和方法[9]，假設入射脈沖為啁啾高斯脈沖，模型中采用不同的重疊函數，具體表現為脈沖表達式的不同；同時考慮到多信道組合的情形，計算出了多個信道組合情況下的FWM噪聲標準差值，詳細推導了啁啾高斯脈沖在色散管理光纖鏈路中的振幅表達式，得出此種情況的簡并FWM噪聲標準差的理論計算模型。通過對此模型仿真計算，仿真計算結果分析表明：脈沖特征寬度對FWM噪聲標準差的影響比較明顯，FWM噪聲標準差值隨脈沖特征寬度的增加而增加；當歸一化的特征寬度較小時，啁啾參數對FWM噪聲標準差的影響不可忽略，優化的啁啾參數值可降低FWM噪聲標準差；優化的色散管理方案可以使得噪聲標準差有較小的值；對局部群速度色散系數絕對值進行優化，可得到較小的噪聲標準差值。

1 理論計算模型

色散管理的色散圖設計如圖1所示,該色散圖中的色散管理單元是由具有群速度色散系數符號相反、絕對值相等且長度可變的兩段光纖組成，放大器間隔等于色散圖周期，放大器與色散管理單元的位置關系如圖1所示。修正文獻[9]中的理論計算模型會發現，這一模型考慮的矩形脈沖波在光纖鏈路傳播過程中，其波形變化幅度較小而被忽略。當入射脈沖為啁啾高斯脈沖時，啁啾高斯脈沖在光纖鏈路傳播過程中，其脈沖形狀會出現較大幅度的周期性振蕩，這種脈沖形狀的周期性振蕩會導致理論計算模型和已有模型中的重疊函數存在差異。

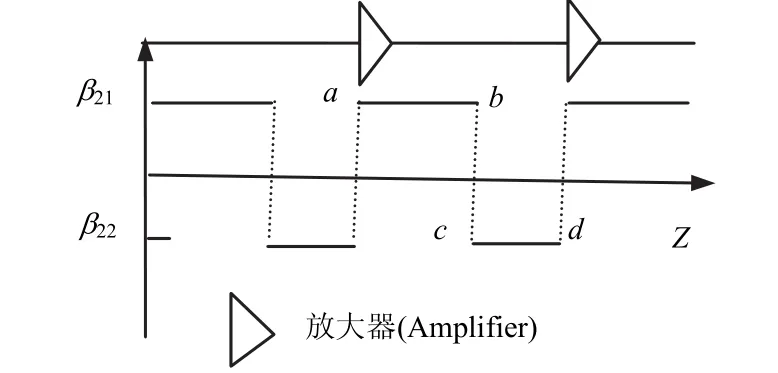
圖1 色散圖及放大器的設置

假設Pimax為信道i內的入射脈沖的峰值功率，T為比特周期，ni為第i信道內的比特序列中的某個比特的序號，τi～a為信道i內的比特序列在a點相對于光波在鏈路初始點的時延，τi～0為第i信道在鏈路初始點的時延；在第i信道內，設 0 ＜ τi～0＜T ,比特信息為“1”時，比特序號為ni，且峰值功率歸一化的啁啾高斯脈沖在第R個色散管理單元入射點a點的光波的電場的復振幅可表示為：

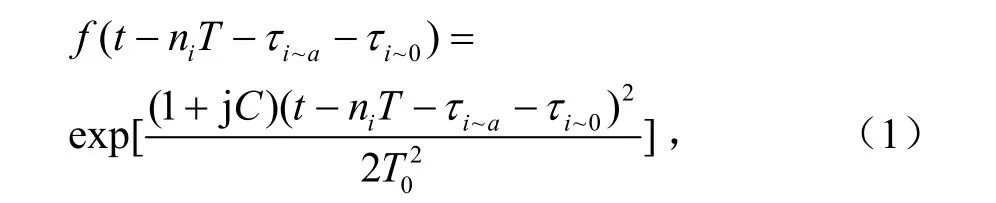
式中，C為初始啁啾參量，T0為特征寬度（光強在峰值的1/e處）。

考慮到采用色散管理的情況，在ab段內，光脈沖傳輸到相對a點距離為za的光場復振幅方程為：

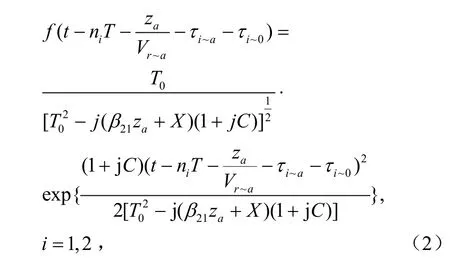
式中，X表示前R-1段光波傳輸過程中的色散積累值，β21是色散圖中群速度系數為正、長度為L1的群速度系數。

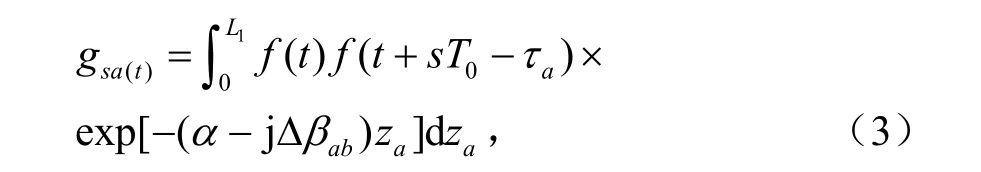
式中，Δβab為相位失配因子，aτ為第二信道相對于第一信道在脈沖傳輸到距離為za時的延遲：

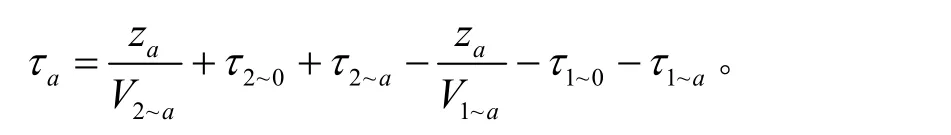
同理可得在經過第R個色散管理單元中的cd段時，其重疊函數與段類似，考慮到位相和延遲的變化后，最大的區別在于啁啾高斯脈沖波形在色散管理單元內的不同；在第i信道內，比特序號為ni的且峰值功率歸一化的啁啾高斯脈沖在色散管理單元在段內，光脈沖傳輸到相對c點距離為zc的光場復振幅方程為：

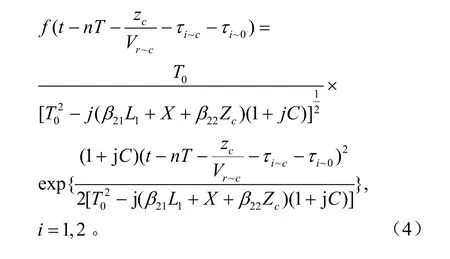
對文獻[9]中的理論計算模型進行修正、求解FWM噪聲標準差的過程中，求解出重疊函數的表達式尤為重要。對于矩形脈沖波，不考慮色散效應的情況下，重疊函數可被直接積分出解析表達式，而對于考慮到群速度色散效應的入射脈沖波為啁啾高斯脈沖的情況，重疊函數求不出解析表達式，只能得到數值積分結果。

2 仿真計算結果及討論

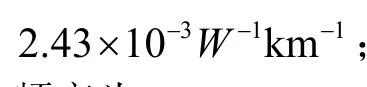
圖2的參數設置：對高斯脈沖的特征寬度進行歸一化處理，x軸表示脈沖的特征寬度與脈沖的初始比特周期之比（）；高斯脈沖的特征寬度隨傳輸距離的變化而變化，這一變化對FWM噪聲標準差的值產生了一定的影響。圖2分3種情況進行了討論，色散管理單元個數R分別取值為：5,8和10；各信道啁啾參數均設為0.2，局部群速度系數的絕對值為，每個色散管理單元中群速度為正的光纖長度占管理單元長度之比為0.2。由圖2可以看出，噪聲標準差隨高斯脈沖的特征寬度增加而增加。

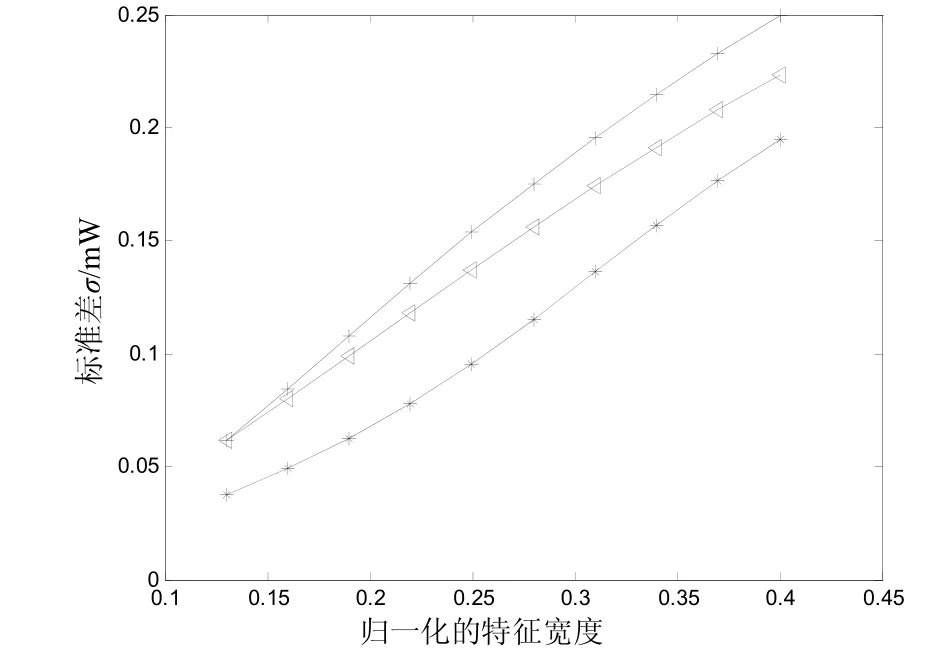
圖2 σ與歸一化的特征寬度T0／T的關系（▽,*,+分別對應色散周期數為5,8和10的情況）

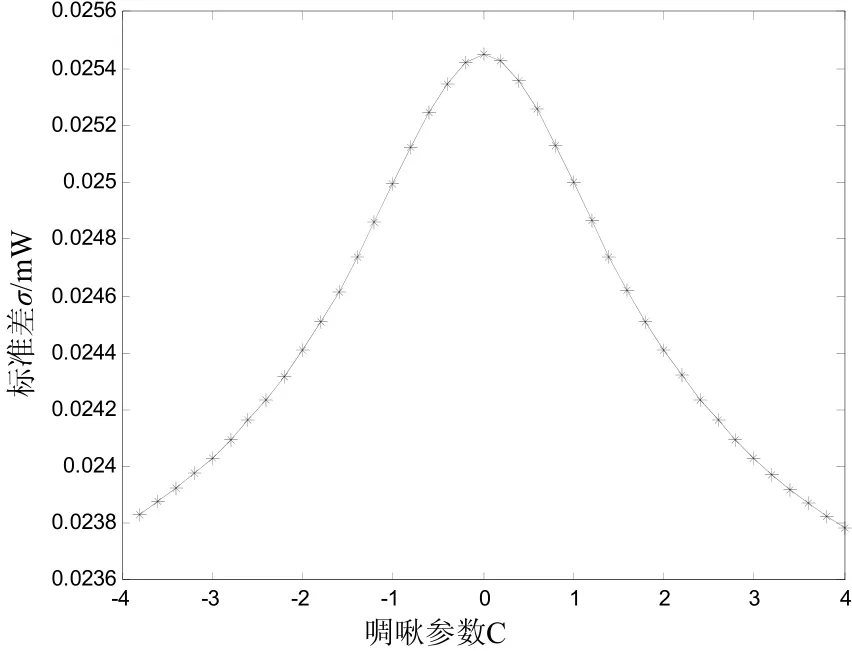
圖3 σ與啁啾參數的關系（T0／T=0.05，=1ps2/km ）

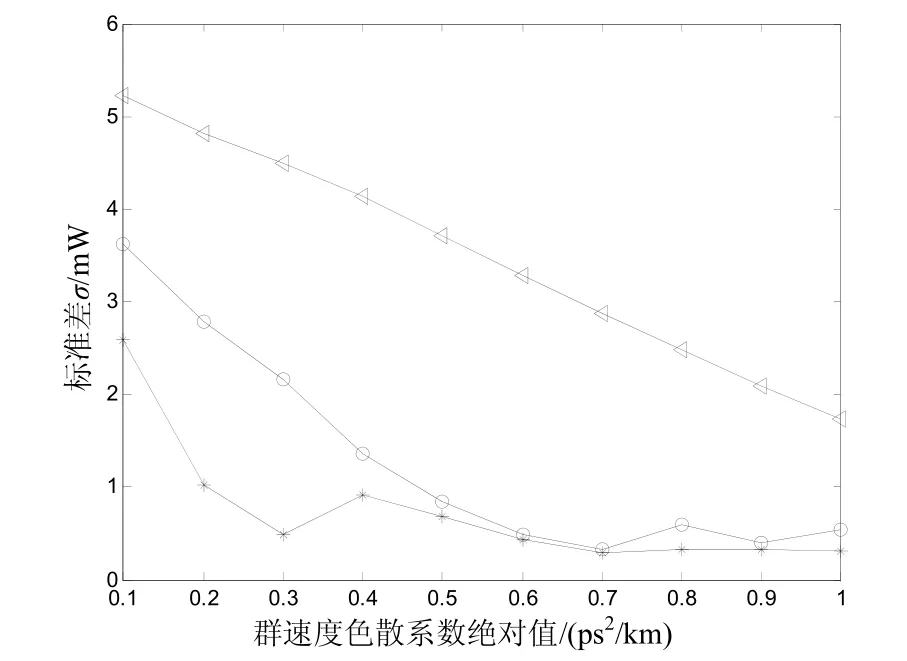
圖4 σ與群速度色散系數絕對值的關系（T0／T=0.2）

3 結語

已有的強度調制直接檢測波分復用系統中簡并FWM噪聲標準差的理論計算模型是基于入射波為連續波，或為矩形脈沖波，但沒有考慮色散管理的情況以及各信道色散效應導致的脈寬展寬的情況下得到的。文中假設入射脈沖為啁啾高斯脈沖并且考慮到色散管理的情況和各信道色散效應的情況下分析了簡并FWM噪聲標準差與系統參數之間的一些關系，數值計算結果表明除了群速度色散、色散管理方案等是影響此種標準差的重要因素外，當入射脈沖的脈寬較小時，各信道比特序列的相對初始時延、初始啁啾參量及脈寬隨距離的變化都對這種標準差的值有較大影響。

[1]INOUE K.Four-wave Mixing in an Optical Fiber in the Zero-dispersion Wavelength Region [J].J.Lightwave TechnoI.,1992,10(11):1553-1561.

[2]TKACH R W,CHRAPLYVY A R,FORGHIERI F,et a1.Fourphoton Mixing and High-speed WDM Systems[J].J.Lightwave Techno1.,1995,13(05):841-849.

[3]BOGONI A,POTI L,BONONI A.Accurate Measurement of In-band FWM Power in DWDM Systems over Nonzero Dispersion Fibers[J].IEEE Photonics Technology Letters,2003,15(02):260-262.

[4]SINKIN O V,GRIGORYAN V S,MENYUK C R.Accurate Probabilistic Treatment of Bit-pattern-dependent Nonlinear Distortions in BER Calculations for WDM RZ Systems[J].Lightwave Techno1.,2007,25(1o):2959-2967.

[5]INOUE K,NAKANISHI K,ODA K,et a1.Crosstalk and Power Penalty Due to Fiber Four-wave Mixing in Multi-channel Transmission Transmissions[J].Lightwave Techno1.,1994,l2(08):1423-1439.

[6]KUMAR S.Analysis of Degenerate Four-wave-mixing Noise in Return-to-zero Optical Transmission Systems Including Walk-of[J].Lightwave Techno1.,2005,23(01):310-320.

[7]杜建新.DWDM系統啁啾高斯脈沖簡并四波混頻噪聲標準差的計算[J].量子電子學報,2009,26(06):736-743.

[8]WU M,WAY W I.Fiber Nonlinearity Limitations in Ultra-dense WDM Systems[J].J.Lightwave Techno1.,2004,22(06):1483-1497.

[9]杜建新.色散管理波分復用系統中的簡并四波混頻噪聲[J].光學學報,2009,29(09):2361-2367.

[10]DU Jianxin, LOU Qihong.Collision-induced Timing Jitter in Dispersion-managed WDM Soliton System with Filtering[J].Chin.opt.Lett.,2004,2(12):688-690.

[11]朱軍,柴曉冬,劉志超.多模光纖鏈路信號傳輸特性分析[J].通信技術,2008,41(10):15-16.

[12]劉飛,張曉峰,張秀珍.多路數據光纖傳輸系統[J].通信技術,2008,41(10):21-22.