一維傾斜場伊辛模型中的糾纏特性*

王琪 王曉茜

(長春理工大學理學院,長春 130022)

1 引言

近些年來,由于量子糾纏在量子計算、稠密編碼和量子隱形傳態等技術中起到關鍵作用,所以量子糾纏的確切量子力學特性備受關注.量子糾纏被認為是量子通信和量子計算的關鍵物理資源.

最近的一些研究發現,系統的可積性和不可積性對系統的兩體糾纏和整體糾纏有著微妙的影響.開始對不可積體系中的多體糾纏的研究用Harper模型[1-3],而隨后的工作則用到量子baker映射[4]、Frenkel-Kontorova模型[5]和無序自旋鏈[6](disordered spin chains).而后Lakshminarayan和Subrahmanyam[7]利用受激伊辛模型討論了系統的可積性和不可積性對兩體糾纏及整體糾纏的影響,結果表明系統的不可積性促進整體糾纏生成,不可積性還會使平均糾纏度增大.近期另外的一些研究討論了Dicke模型經典相空間與量子動力學演化之間的關系,由體系的整體糾纏動力學特性,發現可以更好地揭示相空間的混沌和規則結構[8].Wang等[9,10]研究了QKT(quantum kiched top)模型中量子混沌對自旋壓縮和量子糾纏的影響.伊辛模型作為最簡單的海森堡模型[11,12],是一個簡單而且現實的固態系統,這種模型可以十分理想地制備和控制量子糾纏.對伊辛模型中量子糾纏特性的研究將會有效推動量子計算機的研究和量子信息科學的發展.

基于上面的分析,本文利用一維傾斜場伊辛模型來對量子糾纏特性進行研究[13].并發度(concurrence)[14]和Q測量函數(Q measure)[15]分別是兩種不同的糾纏的度量方法.前者是1998年由Wootters首次提出的,并發度很好地度量了系統的兩體糾纏,而后者是2002年由Meyer和Wallach定義的,可以對系統整體糾纏進行度量.本文討論了從可積到不可積范圍內自旋鏈中的兩體糾纏和整體糾纏特性,但是對于系統的兩體糾纏只涉及近鄰自旋之間的相互作用,同時這些相互作用是平移不變的.并且了解到在一維傾斜場伊辛模型中,不可積性會抑制兩體糾纏,但卻能促進系統整體糾纏生成.不可否認的是,對糾纏的整體度量只是最近才開始探索,而且似乎在多體量子態情況下,不同形式糾纏的度量應該用到不同的方法,這些情況都需要更進一步的闡明.

2 并發度和Q測量函數

1998年由Wootters首次提出并發度來描述兩體量子體系的糾纏,也是目前刻畫兩體糾纏最好的度量方法[14].首先,根據兩量子比特混合態密度矩陣ρi,j構建一個自旋翻轉矩陣

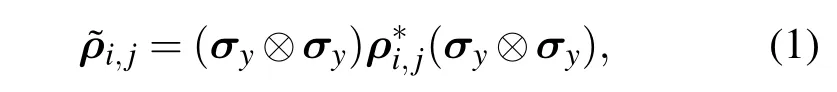
當C=0時,系統沒有兩體糾纏;當C＞0時,系統存在兩體糾纏.

2002年5月,Meyer和Wallach定義了Q測量函數來對整體糾纏進行幾何度量,并且討論了Q測量函數的相關性質.Q測量函數定義如下[15,16]:

2003年,Brennen[17]將Meyer-Wallach Q測量函數做了進一步的推廣,得出如下形式:

其中ρk是對除第k個量子比特外的所有量子比特進行部分求跡后的約化密度矩陣.表征整體糾纏的Q測量函數的取值范圍為0≤Q≤1,當且僅當|ψ〉為乘積態(product state)時Q測量函數為0.當Q測量函數等于1時,說明系統中單個量子比特與剩余量子比特間的整體糾纏最大[18].

3 一維傾斜場伊辛模型

如圖1所示,本文考慮L個自旋為1/2的一維傾斜場伊辛模型[13],我們考慮x-z平面內的傾斜磁場,其哈密頓量可以寫為

其中J為自旋耦合系數,B為外加磁場,L為系統的自旋粒子數,θ決定外場方向,和是Pauli矩陣.這里對于自旋鏈,采用周期邊界條件,即=(i=x,z).當θ=0時,外加磁場方向與自旋方向相同,此時模型是可積的[13],并且系統能級是高度簡并的.當θ=90?時,外加磁場方向與自旋方向垂直,稱為橫場伊辛模型,此時模型也是可積的,并且可以利用Jordan-Wigner變換[19,20]來對橫場伊辛模型進行求解.當0＜θ＜90?時,模型是不可積的[13].本文對一維傾斜場伊辛模型在可積情況和不可積情況下的兩體糾纏及整體糾纏進行討論.

圖1 自旋為1/2的一維傾斜場伊辛模型,考慮x-z平面內的傾斜磁場,自旋鏈滿足周期邊界條件

首先,我們考慮一維傾斜場伊辛模型基態的糾纏特性.圖2中紅色虛線描述的是近鄰兩量子比特之間的糾纏特性,用并發度來度量,本文中的并發度考慮的是近鄰情況下的兩體糾纏,即兩量子比特混合態密度矩陣ρi,j可以表示為ρi,i+1情況時所對應的并發度;藍色實線描述了每個量子比特與剩余量子比特之間的糾纏特性,用Q測量函數來度量.當用并發度來刻畫系統的相變情況時,可以發現,隨著磁場傾角的增大,對應于發生相變時的磁場強度會減小.另外,Q測量函數隨著磁場強度的增加由1逐漸減小,最后趨近于0.而且還可以發現,當磁場強度增大到某值后,并發度會大于Q測量函數的值,說明此時系統中的兩體糾纏較大,整體糾纏會隨著磁場場強的增大而減小.圖2中比較特殊的是磁場傾角θ=0時的情況,此時磁場方向與粒子自旋方向相同,而且系統是可積的.可以看到,在這種特殊情況下并發度始終為0,說明系統中始終不存在兩體糾纏.而Q測量函數會在磁場強度B=2時馬上變為0,而且在磁場場強B＞2以后,Q測量函數會一直為0,說明系統中的整體糾纏也會消失.

圖2 系統基態并發度C(紅色虛線)和Q測量函數(藍色實線)與外加磁場B的關系,磁場方向分別取θ=0,θ=π/6,θ=π/3,θ=π/2,耦合系數J=1,系統粒子數L=8

進一步,我們研究并發度和Q測量函數在一維傾斜場伊辛模型中的動力學特性.選取自旋相干態|1〉?L為系統的初態,其中|1〉表示粒子自旋向上,L表示粒子數目.從而得到初態的時間演化是 |ψ(t)〉=exp(-iHt)|ψ(0)〉,相應的密度矩陣為ρ =|ψ(t)〉〈ψ(t)|.

在確定耦合系數J=1,磁場場強B=1及自旋粒子數目L=8的條件下,我們計算并發度和Q測量函數的時間演化.圖3給出了磁場傾角分別為θ=0,θ=π/6,θ=π/3,θ=π/2情況下并發度的動力學演化曲線.當磁場傾角為θ=0或θ=π/2時,系統是可積的;當磁場傾角分別為θ=π/6和θ=π/3時系統是不可積的.由圖3可以發現,在不可積情況下,并發度在最初得到最大值后會迅速減小直至為零,此時系統沒有兩體糾纏.并且可以發現,系統處在不可積情況下,系統會長時間沒有兩體糾纏.而當系統可積時,一般情況下具有兩體糾纏,只有很短的時間內沒有兩體糾纏.

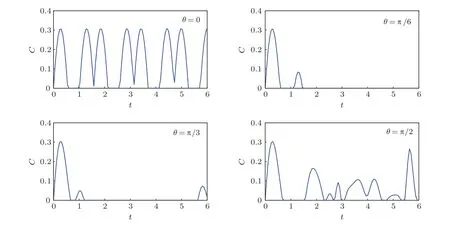
圖3 磁場傾斜角度不同情況下,并發度隨時間的動力學演化曲線 系統參數取值分別為J=1,B=1,L=8

圖4給出了磁場傾角分別為θ=0,θ=π/6,θ=π/3,θ=π/2情況下Q測量函數的動力學演化曲線.同樣,當磁場傾角為θ=0或θ=π/2時,系統是可積的;當磁場傾角分別為θ=π/6和θ=π/3時系統是不可積的.由圖可以發現,在不可積情況下,由Q測量函數表征的系統的整體糾纏最初由0迅速取得最大值,而且在隨后的演化過程中整體糾纏的幅度變化不大.而在系統可積的情況下,整體糾纏的變化幅度明顯比不可積的情況下要大.

對比圖3和圖4可以得到這樣的結論:在系統參數相同的情況下,并發度為0或較小時,系統的整體糾纏通常都處在較大值.并且可以說明在一維傾斜場伊辛模型中,不可積性會抑制兩體糾纏,但卻會促進系統整體糾纏生成.

圖4 磁場傾斜角度不同情況下,Q測量函數隨時間的動力學演化曲線 系統參數取值分別為J=1,B=1,L=8

圖5和圖6更全面地考慮了磁場傾角和磁場場強對并發度及Q測量函數的影響,并且可以看出在足夠長的時間內平均值的穩定性變化.這里考慮粒子數L=8(更多自旋粒子數目時與8自旋粒子情況本質上是相同的),耦合系數J=1時,200次時間演化過程.由圖5可以看到,當取磁場場強B=1時,隨著磁場傾角的增大,最初系統并發度的時間平均值有極小的增加,而后迅速減小,在減小到一定值后,并發度的時間平均值又有了極小幅度的增加,并且在磁場傾角為θ=π/2時,并發度的時間平均值取到了一個較大值.當取磁場場強B=2時,隨著磁場傾角的增大,最初系統并發度的時間平均值迅速減小,減小到一定值后又開始震蕩增大,在磁場傾角為θ=π/2時,系統并發度的時間平均值取到了最大值.由圖6可以看到,在磁場強度不變的情況下,隨著磁場傾角的增大,Q測量函數的時間平均值會先增大而后又減小.而磁場場強B=2的情況下,Q測量函數的時間平均值的增大和減小的幅度都大于磁場場強B=1的情況.最后可以知道,系統的不可積性使Q測量函數的時間平均值增大,相反會使并發度的時間平均值減小.同樣說明了在一維傾斜場伊辛模型中,不可積性會抑制兩體糾纏,而相反會促進系統整體糾纏生成.

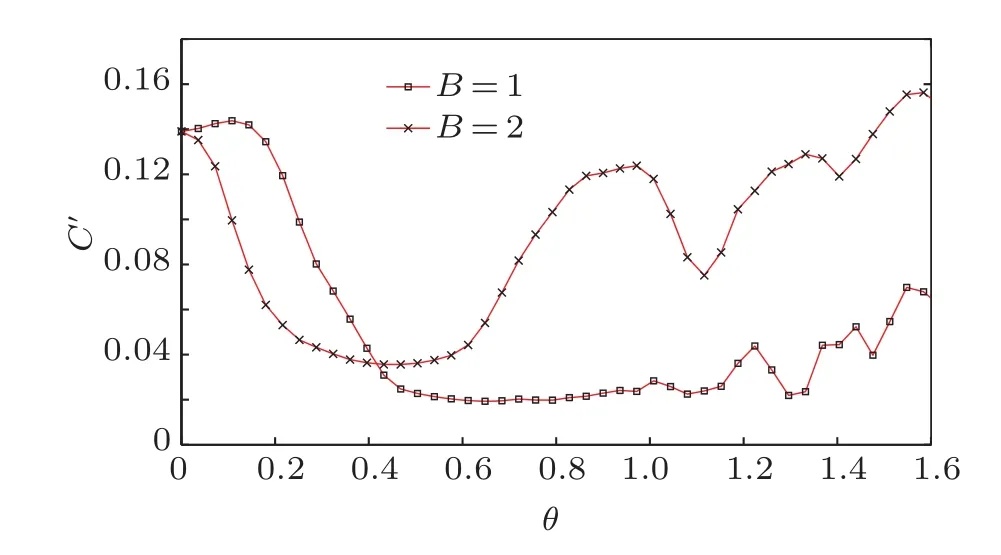
圖5 磁場強度分別為B=1,B=2時,系統并發度的時間平均值隨磁場傾斜角度變化的演化曲線,參量取值分別為J=1,L=8

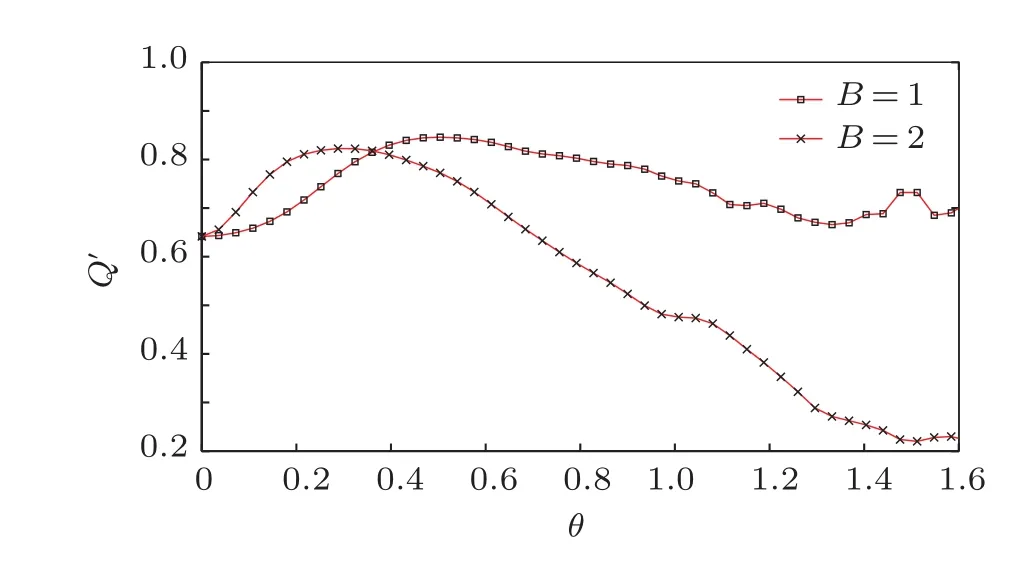
圖6 磁場強度分別為B=1,B=2時,系統Q測量函數的時間平均值隨磁場傾斜角度變化的演化曲線,參量取值分別為J=1,L=8

4 結論

本文對一維傾斜場伊辛模型中的量子糾纏特性進行了討論,運用了并發度和Q測量函數對系統的兩體糾纏和整體糾纏進行度量.

1)由系統基態的糾纏特性曲線發現,隨著磁場傾角的增大,并發度所刻畫的系統相變情況發生變化.隨著磁場強度的增大,Q測量函數由最大值1逐漸減小,隨后會趨近于0;并發度由0先增大后減小.在磁場傾角為0時,情況比較特殊,系統始終不存在兩體糾纏,而Q測量函數會在磁場場強B=2時突然由最大值1變為0,說明系統的整體糾纏也消失了.

2)選取自旋相干態|1〉?L為系統的初態,得到初態的時間演化(模型中參數分別取耦合系數J=1,外場場強B=1及粒子數目L=8).可以發現在一維傾斜場伊辛模型中,不可積性會抑制兩體糾纏,但卻會促進系統整體糾纏生成.

3)在一維傾斜場伊辛模型中,考慮并發度和Q測量函數的時間平均值隨磁場傾角的演化曲線,進一步說明了不可積性會抑制兩體糾纏,但卻會促進系統整體糾纏生成.

今后以一維傾斜場伊辛模型為基礎還有很多有意義的問題可以考慮,我們可以考察系統的不可積性對非近鄰兩體糾纏的影響,或系統的不可積性對量子關聯的影響.還可以考慮其他種類多體糾纏的情況,例如真實多體糾纏[21-23](genuine multipartite entanglement).

[1]Lakshminarayan A,Subrahmanyam V 2003 Phys.Rev.A 67052304

[2]Gu B J,Ye B,Xu W B 2008 Acta Phys.Sin.57695(in Chinese)[顧斌杰,葉賓,須文波2008物理學報57695]

[3]Ye B,Gu R J,Xu W B 2007 Acta Phys.Sin.563718(in Chinese)[葉賓,谷瑞軍,須文波2007物理學報563718]

[4]Scott A J,Caves C 2003 J.Phys.A 369553

[5]Wang X,Ghose S,Sanders B C,Hu B 2004 Phys.Rev.E 70016217

[6]Santos L F,Rigolin G,Escobar C O 2004 Phys.Rev.A 69042304

[7]Lakshminarayan A,Subrahmanyam V 2005 Phys.Rev.A 71062334

[8]Song L J,Yan D,Gai Y J,Wang Y B 2011 Acta Phys.Sin.60020302(in Chinese)[宋立軍,嚴冬,蓋永杰,王玉波2011物理學報 60020302]

[9]Wang X Q,Ma J,Zhang X H,Wang X G 2011 Chin.Phys.B 20050510

[10]Wang X Q,Ma J,Song L J,Zhang X H,Wang X G 2010 Phys.Rev.E 82056205

[11]Qin M 2010 Acta Phys.Sin.592216(in Chinese)[秦猛2010物理學報592216]

[12]Yang Y,Wang A M 2013 Acta Phys.Sin.62130305(in Chinese)[楊陽,王安民2013物理學報62130305]

[13]KarthikJ,SharmaA,LakshminarayanA2007Phys.Rev.A75022304

[14]Wootters W K 1998 Phys.Rev.Lett.802245

[15]Meyer D A,Wallach N R 2002 J.Math.Phys.434273

[16]Scott A J 2004 Phys.Rev.A 69052330

[17]Brennen G K 2003 Quantum Information and Computation(Vol.3)(Berlin:Springer)pp619–626

[18]Castro C S,Sarandy M S 2011 Phys.Rev.A 83042334

[19]Jordan P,Wigner E 1928 Z.Phys.47631

[20]Sachdev S 1999 Quantum Phase Transitions(London:Cambridge U-niversity Press)p46

[21]Ma Z H,Chen Z H,Chen J L 2011 Phys.Rev.A 83062325

[22]Chen J L,Deng D L,Su H Y,Wu C F,Oh C H 2011 Phys.Rev.A 83022316

[23]Deng D L,Gu S J,Chen J L 2010 Annals Phys.325367