利用超相對論量子分子動力學模型研究交變梯度同步加速器能區Au+Au碰撞中的核阻止效應*

袁穎

(廣西師范學院物理與電子工程學院,南寧 530023)

1 引言

超相對論能區重離子碰撞為研究極高溫度、密度條件下的強反應物質提供了機會[1-4].在高能核碰撞中會形成反應粒子的強激發體系[5].在此條件下夸克-膠子等離子體將會形成,可以利用輸運模型研究熱密核物質的許多基礎特性.目前輸運模型有很多,目的都是為了對粒子和核物理實驗中粒子探測器得到的末態強子分布進行準確模擬[6].

人們試圖從重離子碰撞數據中獲得熱密核物質的性質,這就需要對核阻止信息進行深入研究.事實上,人們可以通過研究反應末態的碎塊(或者自由核子)在橫、縱方向的快度分布來獲得核阻止信息[7].

為了研究核阻止效應,本文首先簡要介紹超相對論量子分子動力學(UrQMD)模型、核子-核子彈性散射反應截面的介質修正以及新的碎塊形成判斷條件.其次,將利用此模型得到的理論計算結果與實驗數據進行比較.研究表明,考慮了上述條件后,UrQMD模型能夠很好地描述交變梯度同步加速器(AGS)能區的自由質子快度分布.

2 超相對論量子分子動力學模型

UrQMD模型是一種基于所有重子在軌道上協變傳播的微觀輸運理論[8].UrQMD模型給出了一系列耦合積分-微分方程的Monte Carlo解,這些方程是各種粒子(N,Δ,Λ等)的相空間密度隨時間的演化[9].該模型主要用于描述德國重離子同步加速器(SIS)能區、美國相對論重離子對撞機(RHIC)能區和瑞士大型強子對撞機(LHC)能區的質子-質子、質子-核、核-核碰撞[10].它合并了不同的反應機制,能夠給出各種實驗觀測量的理論模擬結果.一般而言,在研究強子的輸運過程時,需要考慮粒子的平均場勢、兩體散射反應截面[11]和碎塊的形成判斷條件三個因素.

2.1 平均場勢

與量子分子動力學模型相同,UrQMD模型也是基于平行原則.在相空間中,強子用高斯波包表示,并根據下列哈密頓運動方程來傳播[12]:

在標準UrQMD模型中,勢能U包括兩體Skyrme項、三體Skyrme項、Yukawa項、Coulomb項和Pauli項[8,12],即

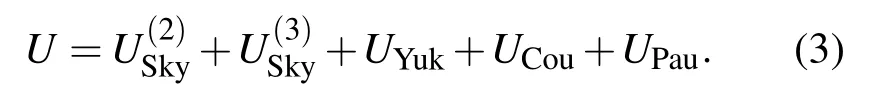
在高能區,重子的Yukawa勢、Pauli勢和對稱勢可以忽略,但Skyrme勢和動量相關項仍然影響著重離子碰撞的整個動力學過程[13].在強子的形成過程中,“預形成”粒子被認為是自由流,且減小的反應截面也僅僅是對領頭強子而言的.在考慮了形成和“預形成”粒子的平均場勢后,UrQMD模型的理論計算結果與實驗結果符合得很好[10,14].

2.2 核子-核子彈性散射反應截面的介質修正

在AGS能區,除了考慮平均場勢的修正外,還需考慮兩核子間反應截面的介質修正.本文只考慮了彈性散射反應截面的介質修正,非彈道仍采用實驗上自由空間的反應截面.共考慮了核子-核子彈性散射反應截面的σfree和兩種形式.這里σfree為自由的核子-核子彈性散射反應截面;為介質修正后的核子-核子彈性散射反應截面[15],

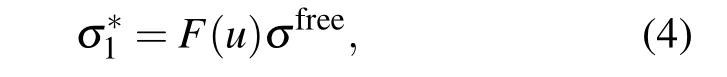
其中介質修正因子F依賴于核縮減密度u,即

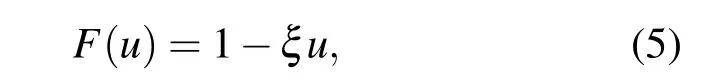
這里ξ=0.5,u=ρi/ρ0,且不考慮動量約束.

2.3 新的碎塊形成判斷條件

在中低能區,碎塊形成的判斷條件通常有兩種形式.一種是最小生成樹(minimum spanning tree,MST)模型:dr＜3.0 fm,dp＜0.2,其中,dr=-為兩核子相對距離,dp=-為兩核子相對動量.另一種是同位旋依賴的最小生成樹(Isospin dependent minimum spanning tree,Iso-MST)模型[16]:drpp＜=3 fm,drnp,nn＜=6 fm,dp＜0.25 GeV/c,其中,,和分別為質子-質子、質子-中子和中子-中子間相對距離.

由蘭州大學王永佳在2012年超重核合成機制與性質研討會上的報告可知,在反應條件相同的情況下,隨著入射能量的增加,運用這兩種判斷條件后自由質子的產額越來越接近,說明在高能區這兩種判斷條件給出的結果相似.

所以,在AGS能區本文采用MST模型的碎塊形成判斷條件,即 dr＜5.0 fm,dp＜0.5 GeV/c.同時得到的自由質子產額為=,其中,Nfreep為運用碎塊形成條件判斷后UrQMD模型計算得到的自由質子產額,為最終計算得到的自由質子產額,α為減小因子.在此模型中,α由理論計算結果與實驗結果擬合得到.

3 AGS能區自由質子快度分布

由于實驗上沒有提供在高能區粒子的橫向快度分布,所以一般僅采用粒子的縱向快度分布來描述核阻止效應[10].Yuan等[10]發現,加入形成和“預形成”粒子的平均場勢后模型的計算結果在中心快度區比實驗結果高.因此,本文考慮在UrQMD模型(3.3版)中加入形成和“預形成”粒子的平均場勢、核子-核子彈性散射反應截面的介質修正和新的碎塊形成判斷條件.

圖1所示為2A GeV的Au+Au中心碰撞(σ/σT＜5%)產生的自由質子快度分布.這里2A GeV表示實驗中單個入射核子的能量為2 GeV,σ為射彈與靶的反應截面,σT為總反應截面.圖1中的曲線代表利用UrQMD模型計算得到的理論結果,其中,實線為僅考慮自由的核子-核子彈性散射反應截面(σfree)的級聯(Cascade)UrQMD模型的計算結果,短劃線為加入形成和“預形成”粒子軟平均場勢(pf-part&f-B SM-EoS)和沒有考慮核子-核子彈性散射反應截面介質修正的UrQMD模型的計算結果,點線為加入形成和“預形成”粒子軟平均場勢和考慮介質修正后的核子-核子彈性散射反應截面()的UrQMD模型的計算結果,模擬中運用了碎塊形成判斷條件dr＜5.0 fm,dp＜0.5 GeV/c,數據點是E895合作組[17]的實驗結果.從圖1可以看出:在UrQMD模型中加入形成和“預形成”粒子的平均場勢后,中心快度區質子數偏高,但在[0.5,1]快度區內的自由質子分布趨勢與實驗結果相同;加入核子-核子彈性散射反應截面介質修正后,中心快度區質子數略有減少,且沒有改變[0.5,1]快度區間的質子分布趨勢.由此可知,利用UrQMD模型計算2A GeV核阻止效應時,形成和“預形成”粒子的平均場勢與截面介質修正都應考慮.

圖2所示為AGS能區實驗入射粒子能量Elab為2A,4A,6A,8A和11A GeV Au+Au中心碰撞(σ/σT＜5%)中自由質子的快度分布.圖2(a)給出了無核子-核子彈性散射反應截面介質修正的級聯模式UrQMD模型的計算結果,圖2(b)給出了加入形成和“預形成”粒子的平均場勢與截面介質修正后UrQMD模型的計算結果,模擬中運用了dr＜5.0 fm,dp＜0.5 GeV/c的碎塊形成判斷條件.圖2中的數據點是E895合作組[17]和E802合作組[18]的實驗結果.從圖 2可以看出,利用UrQMD模型計算AGS能區核阻止效應時,考慮形成和“預形成”粒子的平均場勢與截面介質修正后,給出的自由質子數分布趨勢更接近實驗結果,且在中心快度區得到的自由質子數隨著入射能量的增加偏差程度進一步減小.

圖3所示為AGS能區2A,4A,6A,8A和11A GeV Au+Au中心碰撞(σ/σT＜5%)中自由質子的快度分布.圖3中實線為加入形成和“預形成”粒子的平均場勢與截面介質修正后UrQMD模型的計算結果,模擬時運用了碎塊形成判斷條件dr＜5.0 fm,dp＜0.5 GeV/c以及自由質子產額=αNfreep,同時給出了α的值;數據點是E895合作組[17]和E802合作組[18]的實驗結果.從圖3可以看出,UrQMD模型計算結果在AGS能區與實驗數據符合得較好,且參數α的值隨著入射能量的增加而增大.

圖1 2A GeV的Au+Au中心碰撞(σ/σT＜5%)中自由質子的快度分布

圖2 AGS能區2A,4A,6A,8A和11A GeV Au+Au中心碰撞(σ/σT＜5%)中自由質子的快度分布 (a)無核子-核子彈性散射反應截面介質修正的級聯模式UrQMD模型的計算結果;(b)加入形成和“預形成”粒子的平均場勢與截面介質修正后UrQMD模型的計算結果

圖3 AGS能區2A,4A,6A,8A和11A GeV Au+Au中心碰撞(σ/σT＜5%)中自由質子的快度分布及相應的α值 (a)Elab=2A GeV;(b)Elab=4A GeV;(c)Elab=6A GeV;(d)Elab=8A GeV;(e)Elab=11A GeV

4 結論

本文運用修正的UrQMD模型研究了AGS能區Au+Au碰撞中的核阻止效應,該模型考慮了核子-核子彈性散射截面介質修正和新的碎塊形成判斷條件.模擬結果表明,考慮了平均場勢、截面修正和碎塊形成后的UrQMD模型能夠很好地再現實驗數據,但在高能區三者之間的關聯及其內部機制還有待進一步研究.

[1]Alt C,Anticic T,Baatar B,Barna D,Bartke J,Betev L,Bia?kowska H,Blume C,Boimska B,Botje M,Bracinik J,Bramm R,Bun?i? P,Cerny V,Christakoglou P,Chung P,Chvala O,Cramer J G,Csató P,Dinkelaker P,Eckardt V,Flierl D,Fodor Z,Foka P,Friese V,G′al J,Ga′zdzicki M,Genchev V,G?dysz E,Grebieszkow K,Hegyi S,H?hne C,Kadija K,Karev A,Kikola D,Kliemant M,Kniege S,Kolesnikov V I,Kornas E,Kowalski M,Kraus I,Kreps M,Laszlo A,Lacey R,van Leeuwen M,L′evai P,Litov L,Lungwitz B,Makariev M,Malakhov A I,Mateev M,Melkumov G L,Meurer C,Mischke A,Mitrovski M,Moln′ar J,Mrówczy′nski S T,Nicolic V,P′alla G,Panagiotou A D,Panayotov D,Petridis A,Peryt W,Pikna M,Pluta J,Prindle D,Pühlhofer F,Renfordt R,Richard A,Roland C,Roland G,Rybczy′nski M,Rybicki A,Sandoval A,Schmitz N,Schuster T,Seyboth P,Sikl′er F,Sitar B,Skrzypczak E,Slodkowski M,Stefanek G,Stock R,Strabel C,Str?bele H,Susa T,Szentp′etery I,Sziklai J,Szuba M,Szymanski P,Trubnikov V,Utvi? M,Varga D,Vassiliou M,Veres G I,Vesztergombi G,Vrani? D,Wetzler A,W?odarczyk Z,Wojtaszek A,Yoo I K,Zim′anyi J 2008 Phys.Rev.C 78034918

[2]Sun J X,Liu F H,Wang E Q 2010 Chin.Phys.Lett.27032503

[3]Wang E Q,Liu F H,Rahim M A,Fakhraddin S,Sun J X 2011 Chin.Phys.Lett.28082501

[4]Liu F H 2008 Chin.Phys.B 17883

[5]Anchishkin D,Muskeyev A,Yezhov S 2010 Phys. Rev. C 81031902(R)

[6]Abdel-Waged K,Felemban N,Uzhinskii V V 2011 Phys.Rev.C 84014905

[7]Reisdorf W,Andronic A,Gobbi A,Hartmann O N,Herrmann N,Hildenbrand K D,Kim Y J,Kirejczyk M,Koczo′n P,Kress T,Leifels Y,Schüttauf A,Tymi′nski Z,Xiao Z G,Alard J P,Barret V,Basrak Z,Bastid N,Benabderrahmane M L,?aplar R,Crochet P,Dupieux P,D?elalija M,Fodor Z,Grishkin Y,Hong B,Kecskemeti J,Korolija M,Kotte R,Lebedev A,Lopez X,Merschmeyer M,M?sner J,Neubert W,Pelte D,Petrovici M,Rami F,deSchauenburg B,Seres Z,Sikora B,Sim K S,Simion V,Siwek-Wilczynska K,Smolyankin V,Stockmeier M,Stoicea G,Wagner P,Wi?niewski K,Wohlfarth D,Yushmanov I,Zhilin A 2004 Phys.Rev.Lett.92232301

[8]Bleicher M,Zabrodin E,Spieles C,Bass S A,Ernst C,Soff S,Bravina L,Belkacem M,Weber H,Stocker H,Greiner W 1999 J.Phys.G 251859

[9]Yuan Y 2010 Ph.D.Dissertation(Taiyuan:Shanxi University)(in Chinese)[袁穎2010博士學位論文(太原:山西大學)]

[10]Yuan Y,Li Q F,Li Z X,Liu F H 2010 Phys.Rev.C 81034913

[11]Zhang Y X,Li Z X,Danielewicz P 2007 Phys.Rev.C 75034615

[12]Danielewicz P,Barker B,Shi L 2009 AIP Conf.Proc.1128104

[13]Li Q F,Bleicher M 2009 J.Phys.G 36015111

[14]Li Q F,Bleicher M,Stocker H 2008 Phys.Lett.B 659525

[15]Klakow D,Welke G,Bauer W 1993 Phys.Rev.C 481982

[16]Zhang Y X,Li Z X,Zhou C S,Tsang M B 2012 Phys.Rev.C 85051602(R)

[17]Klay J L,Ajitanand N N,Alexander J M,Anderson M G,Best D,Brady F P,Case T,Caskey W,Cebra D,Chance J L,Chung P,Cole B,Crowe K,Das A C,Draper J E,Gilkes M L,Gushue S,Heffner M,Hirsch A S,Hjort E L,Huo L,Justice M,Kaplan M,Keane D,Kintner J C,Krofcheck D,Lacey R A,Lauret J,Law C,Lisa M A,Liu H,Liu Y M,McGrath R,Milosevich Z,Odyniec G,Olson D L,Panitkin S Y,Pinkenburg C,Porile N T,Rai G,Ritter H G,Romero J L,Scharenberg R,Schroeder L,Srivastava B,Stone N T B,Symons T J M,Wang S,Wells R,Whitfield J,Wienold T,Witt R,Wood L,Zhang W N 2002 Phys.Rev.Lett.88102301

[18]Akiba Y,Ahle L,Akiba Y,Ashktorab K,Baker M D,Beavis D,Britt H C,Chang J,Chasman C,Chen Z,Chi C Y,Chu Y Y,Cianciolo V,Cole B A,Crawford H J,Cumming J B,Debbe R,Dunlop J C,Eldredge W,Engelage J,Fung S Y,Garcia E,Gonin M,Gushue S,Hamagaki H,Hayano R S,Hayashi S,Heintzelman G,Homma S,Judd E,Kaneko H,Kang J,Kim E J,Kumagai A,Kurita K,Lee J H,Levine M J,Luke J,Miake Y,Mignerey A,Moskowitz B,Moulson M,Muentz C,Nagamiya S,Namboodiri M N,Ogilvie C,Olness J,Remsberg L P,Sako H,Sangster T C,Seto R,Shea J,Shigaki K,Soltz R,Steadman S G,Stephans G S F,Tannenbaum M J,Thomas J H,Videb?k F,Wang F,Wang Y,Wu Y,Xiang H,Xu G H,Yagi K,Yang X,Yao H,Zajc W A,Zhu Q,Zhu F 1996 Nucl.Phys.A 610139