韋布爾分布海雜波的建模與FPGA 實現
陳 鬧
(電子科技大學 成都 611731)
1 引言
隨著現代雷達技術的發(fā)展,雷達雜波的建模與模擬越來越重要。雷達雜波是雷達工作環(huán)境的重要組成部分,雜波的特性對雷達目標檢測算法設計影響巨大。因此在雷達回波模擬器中,能否快速有效地模擬海雜波關系到雷達模擬器的性能參數是否可靠[1]。
目前對海雜波的建模方法主要有統(tǒng)計建模,散射機理建模以及近年來興起的混沌理論和多重分形理論建模[2,3],其中雜波統(tǒng)計建模是最常用的方式。海雜波模擬的實質是產生某種隨機序列,滿足某種特定的條件。目前常用的模擬方法主要有兩種:零記憶非線性法[4](ZMNL:Zero Memory Nonlinearity)和球不變隨機過程法[5](SIRP:Spherically Invariant Random Process)。零記憶非線性法的基本思路是首先產生相關的高斯隨機序列,然后經過某種非線性變換得到所需相關非高斯隨機序列。相比于球不變隨機過程法,零記憶非線性法計算量小,且易形成快速算法,具有良好的通用性。
本文先對海雜波中常用的韋布爾模型進行分析,并給出其零記憶非線性法產生原理,然后進行FPGA 實現。
2 韋布爾分布
典型的海雜波幅度分布模型有瑞利分布(Rayleigh)﹑韋布爾分布(Weibull)﹑對數正態(tài)分布(LogNormal)和K 分布。韋布爾分布是介于瑞利分布和對數正態(tài)分布之間的一種雜波模型,能在更廣的環(huán)境內精確地表示實際的雜波分布。
韋布爾分布的概率密度函數表達式如下所示:
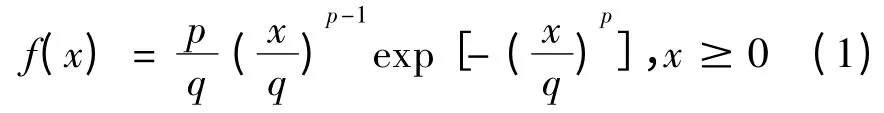
式(1)中,q >0 是尺度參數,表示分布的中位數;p >0 為形狀參數,表示分布的偏斜度。
韋布爾分布概率密度函數分布曲線如圖1所示。
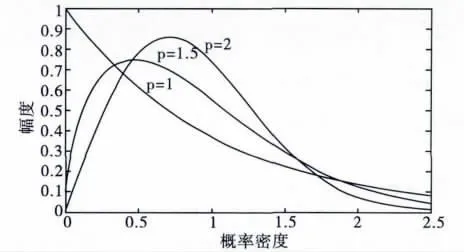
圖1 不同參數韋布爾分布概率密度(q=1)
3 ZNML 法產生韋布爾分布雜波原理
ZNML 法產生韋布爾分布的雜波序列原理如圖2 所 示,ν1,j,ν1,j是不相關的高斯隨機序列;H(ω) 為線性濾波器;u1,j,u2,j是ν1,j,ν1,j通過濾波器H(ω) 后的相關高斯隨機序列,相關系數為ρij;xi為服從韋布爾分布的隨機序列,相關系數為Sij。
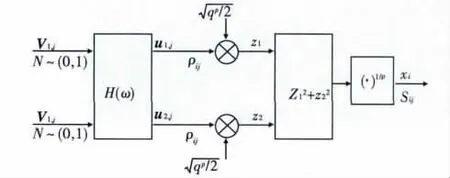
圖2 韋布爾分布序列產生原理框圖
Sij與ρij的關系如式(2):
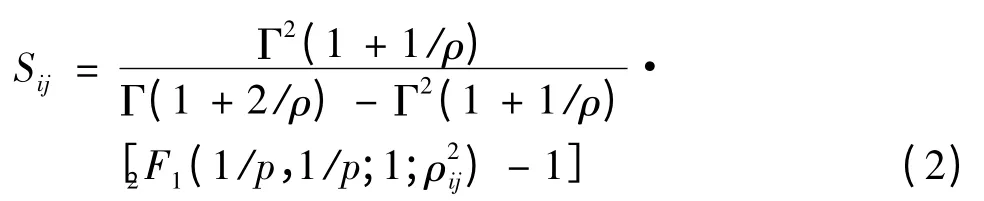
韋布爾雜波產生算法步驟如下:
a.選取合適的采樣率ω,對給定的功率譜密度函數S(ω)進行采樣得到序列
c.由式(2)求出相關系數ρij,i,j=1,2,...,N;
d.利用得到的ρij進行Levinson-Durbin 遞推,得到濾波器系數,產生標準相關高斯隨機序列{un,i},n=1,2,...,N,i=1,2,...,N;
4 韋布爾分布的FPGA 實現
4.1 FPGA 實現流程
韋布爾分布雜波序列的FPGA 實現框圖如圖3所示。
由圖3 可看出,韋布爾分布的實現主要由三部分組成:隨機序列的產生,濾波器的設計,非線性變換。首先通過反饋移位寄存器分別產生兩路均勻分布隨機序列,然后對產生的隨機序列進行BOX-MULLER 變換[6]得到兩路高斯分布隨機序列,將其中一路通過頻域濾波加入時間相關性,最后通過非線性變換得到具有相關性﹑服從韋布爾分布的雜波序列。

圖3 韋布爾雜波分布FPGA 實現框圖
對于FFT ﹑ IFFT 和FIR 濾波器在Xilinx 的庫中都有提供,因此FPGA 實現中最主要的是高斯分布隨機序列的產生。本文采用M 序列發(fā)生器產生均勻分布隨機序列,然后采用基于CORDIC 算法的BOX-MULLER 變換法產生高斯分布隨機序列,其原理框圖如圖4 所示。
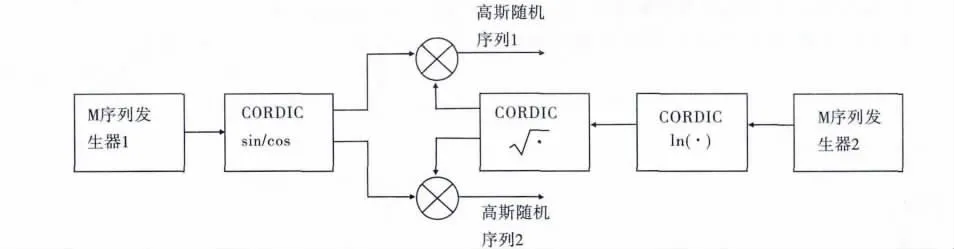
圖4 高斯隨機序列產生原理
4.2 實現結果
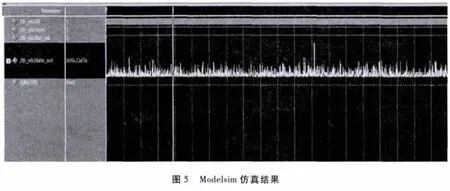
本文采用Xilinx 公司的Spartan-6 系列芯片XC6SLX16-3FTG256C 來實現,選取韋布爾分布的形狀參數p=1.5,尺度參數p=2,功率譜為高斯譜。Modelsim 仿真結果如圖5 所示,將產生的雜波數據導出與理論值對比如圖6 所示,功率譜曲線以及概率密度曲線基本吻合。
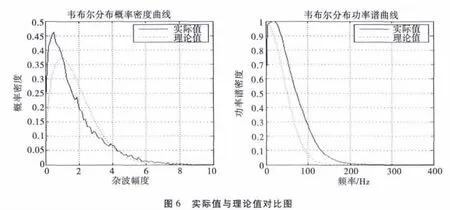
5 結論
本文先對韋布爾分布雜波進行建模分析,闡述了韋布爾分布雜波產生的原理,然后用FPGA 進行硬件實現,且產生雜波序列與理論值分布相吻合,得到了很好的效果,可應用于雷達模擬器的設計中。
[1]周雪峰.船舶導航雷達的回波研究與模擬[D].大連:大連海事大學,2008-03.
[2]K.D Ward,S.Watts.Use of Sea Clutter Models in Radar Design and Development[J].IET Radar Sonar Navig.2010,4(2) :146-157.
[3]張長隆.雜波建模與仿真技術及其在雷達信號模擬器中的應用[D].長沙:國防科技大學,2004.
[4]L.James,Jr.Marier.Correlated K-distribution Clutter Generation for Radar Detection an Track[J].IEEE Transaction On Aerospace and Electronic System,1995,31(2) :568-580.
[5]E.Conte,M.Longo,M.Lops.Modelling and Simulation of Non-Rayleigh Radar Clutter[J].IEE Proceedings-F,1991,138(2) :121-130.
[6]夏陽.三種高斯隨機序列的FPGA 實現分析[J].現代電子術,2011,34(17) :11-14.

