我國技術進步對能源效率影響的實證分析

詹國華，陳治理

（江西財經大學統計學院，南昌 330013）

0 引言

我國各區域的能源發展極不平衡，空間格局的不平衡性也表現在各區域的經濟、技術水平等各方面。能源問題越來越受到世界各國的高度關注，我國也開始重視能源利用效率問題，并提到了國家戰略的高度。

技術進步與能源效率的關系也逐漸被國內外專家學者所關注并取得了一定的研究成果，我國也有專家學者針對我國的能源效率及技術進步與能源效率的關系進行了深入研究。從相關文獻中我們發現我國能源效率存在區域集聚性或區域差異性，因此在分析我國技術進步對能源效率的影響時應當考慮能源效率的空間效應。目前實際的技術進步對我國能源效率研究文獻中，所使用的數據集計量模型，要么只利用時間序列數據，分析隨著時間的推移我國技術進步對能源效率的影響；要么只利用橫截面數據，進行地區與地區之間的靜態的影響研究。然而在實際中，技術進步對能源效率的影響關系是在時間和空間兩個尺度上耦合進行的，僅利用時間序列數據或橫截面數據無法滿足技術進步對能源效率影響分析的需要，也難以深入而深刻地研究技術進步對能源效率影響的動態發展過程及演變機制。因此筆者認為使用考慮空間效應的時間序列和橫截面融合的空間面板數據模型，更能將能源利用效率以及技術進步對能源效率的影響在時間上的變化和跨橫截面的變化在不同時間點上可以將區域性差異分離開來。

1 樣本數據和空間面板模型

1.1 變量選取和樣本選擇

有關能源效率的測度指標有多種，本文選取最常用的宏觀經濟指標，用nyxl表示單位能耗產值，其計算公式為：nyxlit=GDPit/nyxfit。其中，GDPit表示t時期i區域國內生產總值，nyxfit表示t時期i區域能源消費總量，該比值越大說明t時期i區域的能源利用效率越高，反之，則越低。地區國內生產總值數據來源于《2010年中國統計年鑒》，地區能源消費總量數據來源于《2010年中國能源統計年鑒》。

本文選取以下四個反映技術進步的變量：外商直接投資（FDI）、地區研究與試驗發展投入（RD）、人力資本（HC）和專利授權書（PAT）。考慮到統計指標的時間連續性和統計口徑的一致性要求，用各地年末登記的外商投資企業投資額代表外商直接投資，數據來源于《中國貿易外經統計年鑒》（2009、2010）。用各地區研究與開發機構研究與試驗發展經費內部支出代表地區研究與試驗發展投入，數據來源于各年《中國科技統計年鑒》。用各地區研究與開發機構從事科技活動人員數代表人力資本，數據來源于各年《中國科技統計年鑒》，由于2009年數據與以往年份相比統計口徑不一致，本文采取2007、2008年數據的簡單加權平均獲得2009年份的數據。用三種專利授權數代表各地區的專利授權數，數據來源于各年《中國統計年鑒》。因統計年鑒中無西藏地區的能源消費總量數據，因此本文的研究樣本為我國的30個省市自治區，所用數據為2005～2009年30個省市自治區的面板數據或平行數據。

1.2 空間自相關檢驗模型

空間自相關是空間場中的數值集聚程度的一種度量。距離近的事物之間的聯系性強于距離遠的事物之間的聯系性，如果一個空間場中的類似的數值有集聚的傾向，則該空間場就表現出很強的正空間自相關，反之，表現為負空間自相關。因此，空間自相關描述的是某一位置上得屬性值與相鄰位置上得屬性值之間的關系。空間自相關性檢驗分為全局空間相關性檢驗和局域空間相關性檢驗，全局空間自相關整體刻畫我國能源效率的空間集聚特征和區域間的相互作用，Moran I是常用的全局空間自相關性指標，其計算公式如下：

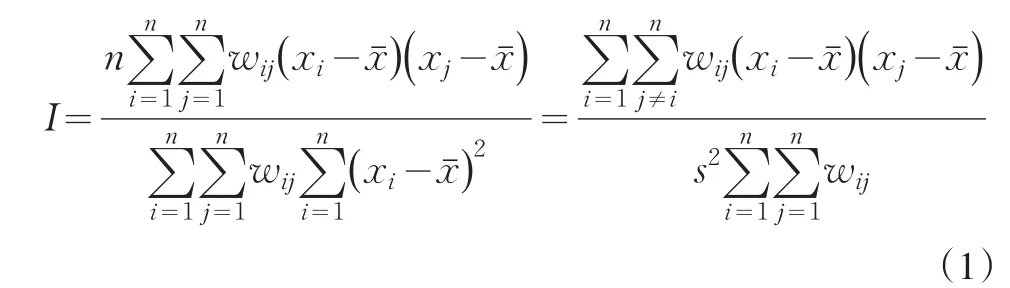
對于Moran I的計算結果，可分別采用漸進正態分布和隨機分布兩種假設進行檢驗（本文采用漸進正態分布），其標準化形式為：

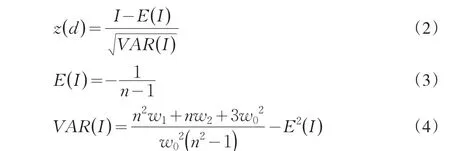
在全局空間自相關顯著而樣本量較大時，全局自相關可能會掩蓋完全隨機化的樣本數據子集，因此有必要進行局域相關性檢驗。其常用的衡量指標是局域Moran I（LISA,空間聯系局域指標），針對某個空間單元i，其計算公式為：

當Ii的取值大于零表示該區域單元周圍相似值（高值或低值）的空間集群，Ii的取值小于零則表示該區域單元周圍非相似值的空間集聚。通過繪制Moran散點圖，可以將我國各省的能源利用效率分為四種類型的集聚模式：HH型、LL型、LH型和HL型，關于四種集聚模式的特征實證分析部分有詳細介紹。

1.3 空間面板模型

Elhorst提出了包括固定效應、隨機效應、固定參數和隨機參數模型在內的面板數據估計方法。在面板數據分析中，通常樣本個體數值之間存在一定的差異，這種差異解釋為固定效應或隨機效應，固定效應是指不同個體之間的差異變動是確定性的，而隨機效應則指不同個體之間的差異變動是隨機性的。當樣本是隨機地抽取于所考察的總體時，設定隨機效應模型更為恰當，然而本文的研究樣本是所有的總體即中國30個省市自治區（除西藏外），因而采用固定效應模型更為合理。固定效應主要包括地區固定效應、時間固定效應和時空固定效應。根據模型設定時對“空間依賴性”的表現方式不同，空間面板計量模型主要分為空間滯后面板模型和空間誤差面板模型，考慮固定效應以后相應的模型變為固定效應空間滯后面板模型和固定效應空間誤差面板模型。

固定效應空間滯后面板模型：

式（7）、（8）中，Y為NT×1因變量，表示各個省份的能源利用效率，X為NT×k的解釋變量矩陣，分別是外商直接投資、國內R&D投入、人力資本和專利授權數，參數β反映的是解釋變量對因變量的影響。IT?W是矩陣的kronecker乘積，IT是T×T的單位矩陣，W為N×N的空間權重矩陣，N和T表示研究對象的個數N=30，研究樣本的時間跨度T=5。η=iT?sF、tF?iN表示矩陣的kronecker乘積，分別對應每個觀測值的地區固定效應列向量和時間固定效應列向量，其中iT和iN分別是T維和N維元素全為1的列向量，sF=(α1,α2,…,αN)T、tF=(δ1,δ2,…,δT)T分別為地區固定效應的N維列向量和時間固定效應的T維列向量。

式（7）中，空間自相關系數ρ意味著一地區影響能源利用效率的解釋變量，都會通過空間傳導機制作用于其他地區，而式（8）中，空間誤差系數λ則反映了鄰近地區能源利用效率的誤差沖擊對本地區能源利用效率的影響程度。這也正是空間滯后模型與空間誤差模型空間依賴性的體現與不同，很好地解決了回歸模型中復雜的空間相互作用于空間依存性問題。

2 實證分析

2.1 實證模型與模型估計方法

文中采用2005～2009年間我國30個省市自治區區劃的面板數據（篇幅有限原始數據略），由于西藏、港澳臺地區的數據不全或指標的統計口徑不一致，不納入分析的范圍。根據面板模型（7）、（8），同時考慮地區固定效應和時間固定效應的影響，可以得到我國技術進步對能源效率影響的空間面板數據模型：

固定效應空間滯后面板模型：

令nyxlt=(n yxl1t,nyxl2t,…,nyxl30t)，表示第t期30個省市自治區的能源利用效率值，研究樣本的時期跨度T=5,t=1，2，3，4,5，將不同時期數據堆迭即得nyxl=(n yxl1,nyxl2,…,nyxl5)T；同理，FDIt=(FDI1t,FDI2t,…,FDI30t)，表示第t期我國30個省市自治區的外商直接投資額，FDI=(F DI1,FDI2,…,FDI5)T,以此類推可以得到其他自變量的表達式。βi(i =1,2,3,4)表示自變量系數，其余參數的含義同模型（7）、（8）。

由于面板模型中存在空間滯后被解釋變量和空間滯后誤差項，傳統最小二乘法（OLS）的估計結果將是有偏或不一致的，通常采用極大似然法（ML）估計空間計量經濟模型，但ML不適合估計引入面板數據的面板模型參數，而用蒙特卡羅方法來近似對數似然函數中雅克比行列式的自然對數是很好的選擇。本文的實證分析主要借助Geoda095i和Matlab7.0軟件完成，程序代碼參考了LeS-age、Elhorst等人編寫的空間計量程序包。

2.2 實證分析步驟與結果

2.2.1 空間自相關性檢驗

首先利用全局自相關檢驗模型（1）、（2）、（3）、（4）計算得到我國區域能源消費的Moran I值以及該Moran I值在近似正態分布的假設條件下的期望值E()I、標準差S()

I、標準化以后的Z值以及相應的概率 p值，2005～2009年我國區域能源利用效率區域空間分布全局Moran I值如下表1：

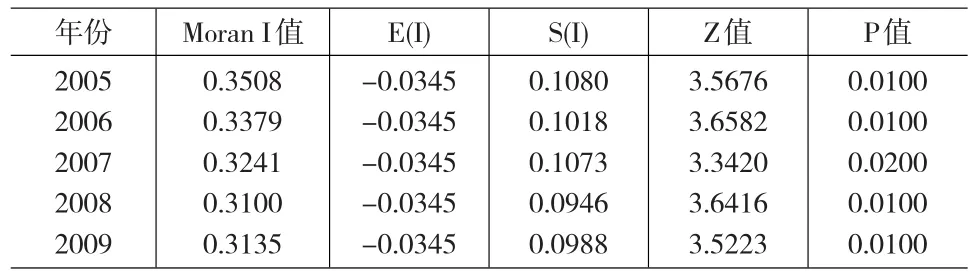
表1 2005～2009年我國能源利用效率區域空間分布的Moran I值

由表1可知，2005～2009年我國30個省市自治區能源利用效率Moran I值的正態統計量Z值均大于正態分布函數在0.05顯著性水平下的臨界值1.96，統計量Z值對應的伴隨概率p值都小于0.05，表明我國區域能源利用效率存在很強的正空間自相關性。也就是說我國區域能源利用效率在空間分布上并沒有表現出完全隨機的狀態，而是存在區域間的空間溢出效應：能源利用效率較高的省份相對的相互鄰接，能源利用效率較低的省份相對的相互靠近，由于有溢出效應的存在，本省的能源利用效率會影響到鄰省的能源利用效率。從總體變動趨勢來看，我國能源利用效率的空間溢出效應應有下降的趨勢，總之，我國能源利用效率的地區分布存在不可忽視的空間維度的正相關性。

為了進一步考察各省市自治區能源利用效率在空間上的集聚模式，根據模型（5）、（6）計算空間聯系局域指標（LISA）。通過計算局域Moran I值及其顯著性檢驗，發現我國能源利用效率各年度之間的HH、HL、LH和LL四種集聚模式的集聚地區變化不大。局域Moran I值較大且顯著的“熱點區”（HH）主要分布在我國東部沿海一帶，上海、浙江、福建、江蘇等地，表示這些省份及其周圍省份都有較高的能源利用效率，而位于西部的甘肅、青海、寧夏、新疆等地處于“盲點區”（LL）,表示這些省份及其周圍省份能源利用效率較低。處于“熱點區”或“盲點區”的省市自治區，其地區能源利用效率的差異不大，存在較強的正空間自相關。處于HL集聚模式的省份主要有北京、天津、河南、吉林和黑龍江，表示這些省份的能源利用效率高于其周邊鄰省，河北、內蒙古、遼寧和湖北則處于LH集聚模式，表示這些省份的能源利用效率低于其周邊鄰省，處于HL和LH集聚模式的省份，存在負空間自相關關系。

通過以上的全局自相關和局域自相關分析可知，我國區域能源利用效率存在不可忽視的空間維度的依賴性和差異性。具體來說，我國區域能源效率呈現出東高西低的空間分布格局；較高能源利用效率的東部沿海地區的溢出效應沒有完全擴散出來，區域能源效率的非均衡性依然存在。

2.2.2 空間面板模型估計

上述Moran I和LISA檢驗結果表明，我國各省市自治區的能源利用效率存在正空間相關性，采用極大似然估計方法，借用Matlab7.0軟件估計空間滯后面板模型和空間誤差面板模型。根據固定效應的不同，得到如下6個模型：SAR（空間滯后模型）的地區固定效應模型、SAR的時間固定效應模型、SAR的時空固定效應模型、SEM（空間誤差模型）的地區固定效應、SEM的時間固定效應模型、SEM的時空固定效應模型。其中，地區固定效應表示不同省份地理特征的影響，時間固定效應表示經濟波動或制度政策的階段性影響，時空固定效應則表示同時考慮不同省份的地理特征和經濟波動對能源利用效率的影響。考慮到各變量數量級不同對回歸方程的影響，回歸方程變量單位調整為如下形式：萬元/萬噸標準煤、百萬美元、萬元、人和件，回歸估計結果如下表2、表3。

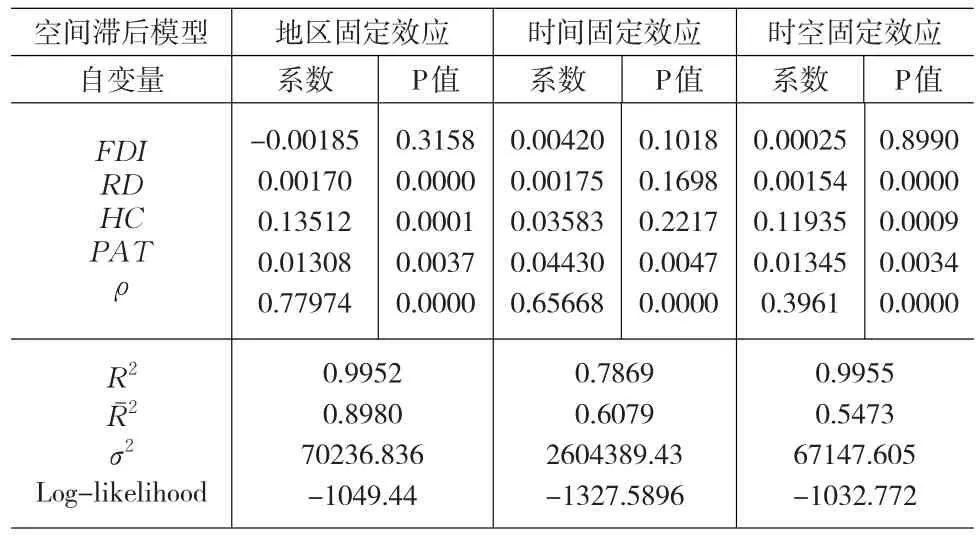
表2 空間滯后面板模型估計結果

在以上的空間滯后模型和空間誤差模型中，地區固定效應、時間固定效應和時空固定效應的系數、相應的概率P值以及擬合優度指標如上表。標志空間依賴關系的空間自相關系數（ρ）和空間誤差系數（λ）在6種情況下都通過了顯著性水平0.01的檢驗，進一步說明我國能源利用效率具有空間依賴現象，鄰近省、直轄市和自治區之間形成了一定的空間依賴作用和正的空間溢出效應。通過表2、表3可知地區固定效應模型的擬合優度都要好于時間固定效應模型，表明能源利用效率在我國的區域分布呈現的區域特征強于階段性或時間性特征，省份之間的個體差異是影響我國能源利用效率空間分布格局的主要因素。

綜合考慮各變量系數及其P值、空間自回歸系數、空間誤差系數和各模型的擬合優度，采用地區固定效應的空間滯后面板模型作為分析工具更準確、合理。由該模型的回歸結果可以知道，RD、HC和PAT變量的伴隨概率P值都小于0.01，說明在我國國內R&投入、人力資本和專利授權數都對提高我國區域能源利用效率都有積極的作用，其中人力資本的回歸系數較大，表明在我國每增加一個人從事科技活動工作，百萬噸標準煤的產值平均將增加0.13萬元。同時也應注意到FDI回歸系數為較小的負值，相應的P值達到了0.3，這說明2005～2009年期間外商直接投資在提高我國能源利用效率方面并沒有發揮積極作用，這與我國長期以來堅持的保持經濟高速增長目標，大力招商引資的政策有關，各級政府片面最求引資的總量而忽視了“資本”的質量問題，先進的技術、設備和高效的管理理念等引進的較少。

3 結論與啟示

影響能源利用效率的因素很多，本文從技術進步這一視角分析了2005～2009年期間其對我國能源利用效率的影響關系，采用空間面板模型很好地揭示了技術進步在時間、空間和時空維度對提高我國能源利用效率的作用機制。

我國區域能源利用效率的全局Moran I和局域LISA分析可知，我國能源利用效率表現出較強的正空間依賴現象，同時各省份的能源利用效率存在一定差異性。總體上來說，我國能源利用效率的區域分布呈現出區域地理特征強于階段性或時間性特征，表現出東部沿海地區能源利用效率較高、而西部地區能源利用效率較低的東高西低格局。國內R&D投入、人力資本以及專利授權數等在促進我國能源利用效率方面發揮了積極的作用，改革開放以來，全國上下把保持經濟增長放在首位，大力積極招商引資，各級政府在招商引資的過程中只注重“量”而忽視了“質”，導致外商直接投資在提高能源利用效率方面沒有發揮到應有的作用。

通過以上的分析，⑴我國能源利用效率的區域依賴性和差異性特點，決定了各省市自治區在制定本地區政策時，應考慮本地區的區域特征，進一步擴大區域能源利用效率正的溢出效應。⑵目前我國處于產業結構調整的關鍵時期，利用該契機，大力發展科技產業，給予研究與開發機構更多的經費投入，培養優秀的科技人才。儲備大量的人力資本，這樣不僅可以提高我國自主創新能力，而且可以更好、更快地學習國外的先進技術和先進的管理理念，使其本土化。⑶地區固定效應空間滯后模型FDI系數在顯著性水平0.05時顯著為零，說明外商直接投資在改善能源利用效率方面并沒有發揮應有的作用。在要求經濟快速增長的同時注重能源效率的提高，這就要求各級政府在招商引資當中，應當注意先進的技術、先進的設備和高效的管理理念的引進，盡可能為其提供優良壞境。⑷最后，國家應重視將東部沿海地區的先進技術轉移至西部地區，使西部地區的能源利用效率得到改善，盡可能發揮能源利用效率較高東部沿海地區的溢出效應的作用。

[1]Elhorst J P.Specification and Estimation of Spatial Panel Data Models[J].International Regional Science Review，2003,26（3）.

[2]Baltagi B H.Econometric Analysis of Panel Data(2ndEdtion)[M].Chichester:Wiley，2001.

[3]Anselin L，Hudak S.Spatial Econometrics in Practice:a Review of Software Options[J].Regional Science and Urban Economics，1992,22（3）.

[4]Barry Ronald P，Pace R Kelley.Monte Carlo Estimates of the Log De?terminant of Large Sparse Matrices[J].Linear Algebra and its Applica?tions,1999,289（1～3）.