諧波齒輪傳動柔輪的變形分析*

祝海林 蔣 宇 王鋮龍 錢志達 寧 鵬

(常州大學機械工程學院，江蘇常州213016)

諧波齒輪傳動是上世紀50年代后期為適應空間科學、宇航尖端技術的發展而出現的一種新型傳動技術，它具有結構簡單、傳動比大、承載能力高、齒面相對滑動速度低、傳動平穩、噪聲小等優點［1］，所以在航天航空、仿生技術、原子反應堆、機床、儀器儀表、機器人、汽車、常規武器、印刷機構及醫學器械等領域得到了廣泛應用［1－2］。

諧波齒輪傳動是通過撓性構件(柔輪)的彈性變形來實現運動和動力的傳遞，工作過程中，柔輪上各點的徑向變形量是不斷變化的，因而其主要失效形式是柔輪的疲勞破壞，特別在承載扭矩較大的場合，經常出現因柔輪的徑向變形量過大而導致柔輪過早發生疲勞損壞。為了提高柔輪與剛輪的嚙合性能、延長諧波齒輪傳動裝置的使用壽命，很有必要對易損件——柔輪的變形情況進行分析。

近年來，有人提出了彈性波發生器的概念，這種波發生器的優點在于通過調整變形力改變柔輪徑向變形量，使柔輪與剛輪的輪齒實現無側隙嚙合［3］。而要實現無側隙嚙合，必須先對柔輪的變形與變形力進行研究。目前，國內主要是對杯形柔輪開展了變形、應力研究，對環形柔輪的理論研究還不深入，設計過程中主要依靠經驗和試驗的方法［2］。為此，本文運用材料力學解決超靜定結構的方法，建立了雙波諧波齒輪傳動環形柔輪變形量、截面彎矩的計算模型，并以Matlab軟件為平臺，對柔輪的徑向變形量與柔輪齒數、中性層曲率半徑變化與柔輪截面位置的關系進行了仿真分析，可為柔輪的性能評價與進一步改進提供理論依據。

1 諧波齒輪傳動的特點

諧波齒輪傳動裝置主要由3個基本件組成，即波發生器1、具有外齒的柔輪2和具有內齒的剛輪3，如圖1所示。通常波發生器為主動件，而剛輪和柔輪之一為從動件，另一個為固定件。按照波發生器上滾輪數的不同，有雙波傳動、三波傳動等，目前最常用的是雙波傳動［4］。在未裝配前，柔輪的原始剖面呈圓形(參見圖2的中性圓1)，柔輪與剛輪的周節相同，波發生器的最大直徑比柔輪變形前的內圓直徑略大。把波發生器裝入柔輪內時，由于波發生器的作用，迫使柔輪產生變形，柔輪變成橢圓(如圖2所示)。

波發生器轉動時，迫使柔輪變為不斷旋轉的橢圓，長軸兩端附近的齒與剛輪的齒完全嚙合、短軸附近的齒則與剛輪的齒完全脫開，其余不同區段上的齒處于逐漸嚙入或嚙出的過渡狀態。波發生器連續轉動時，柔輪的變形部位也隨之轉動，使輪齒依次進入嚙合，然后又依次退出嚙合，從而實現嚙合傳動。諧波齒輪傳動的齒數差等于波數或波數的整數倍，為了實際加工的方便，諧波齒輪的齒形多采用漸開線［4］。

諧波齒輪傳動的基本特點是柔輪連續不斷地變形，柔輪工作在非對稱的應力循環狀態下，其工作條件惡劣，所以柔輪是影響諧波齒輪傳動裝置工作性能的關鍵零件，諧波齒輪傳動裝置的壽命、可靠性、運動精度等主要受到柔輪的限制。由于柔輪的初始變形與剛輪的嚙合相關，為了達到更好的嚙合狀態，就需要準確掌握在裝入波發生器后柔輪的變形情況，以便確定兩種齒輪的嚙合參數。因此，長期以來柔輪的變形與疲勞強度一直是諧波齒輪傳動領域研究的難點和熱點。

2 柔輪的中性層與中性軸

柔輪的變形分析，一般以波發生器與柔輪裝配前后柔輪中性層曲線不伸長為前提條件。所謂中性層，是材料力學里的一種假設，包括幾何中性層、應力中性層和應變中性層。借助于中性層的概念，可以使復雜的材料力學問題得以簡化。

幾何中性層指的是材料(如桿件)內部的中間面，這個面上的每一點到桿件兩邊的法向距離都相等。應力中性層是桿件發生彎曲變形時，其內部切向應力為零的所有點形成的面。根據材料力學的平面假設，可把桿件看成由無數縱向纖維所組成，比較變形區內桿件彎曲前后相應位置的網格線長度可知，靠近外側的纖維受拉而伸長，靠近內側的纖維受壓而縮短，從內、外側至桿件的中心，其縮短和伸長的程度逐漸變小。由于材料的連續性，在伸長和縮短兩個變形區域之間，必定有一個既不伸長也不縮短的過渡層，該層不發生線性應變，這一過渡層就稱為應變中性層。即，在桿件彎曲變形時，應變中性層纖維的長度在彎曲前后保持不變。在桿件發生彈性彎曲時，應變中性層與應力中性層是重合的，且通過桿件橫截面的中心，即也與桿件的幾何中性層重合。

研究材料受力彎曲變形時所說的中性層一般就是指應變中性層，中性層和橫截面的交線，叫做中性軸，即橫截面上正應力為零的各點的連線。當桿件發生平面彎曲，且處于線彈性范圍時，中性軸通過橫截面的形心，且垂直于載荷的作用平面。根據文獻［5］知，桿件平面彎曲時中性層的曲率半徑ρ與截面彎矩M之間存在如下的關系:

式中:ρ為桿件變形后中性層的曲率半徑;E為桿材料的彈性模量;I為桿件截面對中性軸的慣性矩;EI為桿的抗彎剛度;M為在載荷平面內，使桿件產生曲率變化的彎矩。

應變中性層的確定是進行柔輪變形分析、計算的重要依據。當柔輪彎曲變形程度較小時，應變中性層基本上處于柔輪厚度的中心，通常認為應變中性層與幾何中性層重合;但當柔輪彎曲變形程度較大時，應變中性層與柔輪的幾何中心層不重合，而是向柔輪的內側移動。變形量愈大，內移量愈大。

在柔輪與剛輪嚙合過程中，受波發生器的制約，柔輪中性層由圓變成不斷旋轉的橢圓，柔輪環承受交變的彎曲變形。但是中性層在彎曲過程中的長度和彎曲前一樣，即柔輪中性層的長度保持不變，所以中性層是計算柔輪展開長度的基準。柔輪環變形過程中，柔輪的橫截面繞中性軸轉動，橫截面上任一點處的正應力與該點到中性軸的距離成正比，而在距中性軸等距離的同一橫線上各點處的正應力相等。諧波齒輪傳動中，柔輪的彈性變形可視作小變形。研究表明，把柔輪齒圈輪緣的中線(即幾何中性層)作為柔輪的應變中性層已經足夠精確［6］，所以一般認為柔輪的中性層位于柔輪壁厚的1/2處。

3 柔輪變形與截面彎矩數學模型的建立

為了研究柔輪變形與其結構參數之間的關系，必須先建立柔輪截面彎矩的計算模型。由于柔輪是一個具有輪齒的圓柱殼體，直接建立柔輪的力學模型很復雜，一般將其簡化為當量光滑圓柱殼體來進行分析。下面以環型柔輪為例，用圓柱形柔輪作為柔輪中性圓環變形計算的模型，如圖3a的A1B1C1D1所示。在等截面柔輪圓環直徑A1B1的兩端，波發生器對柔輪圓環施加了方向相反的一對F力，顯然這屬于超靜定結構［5］。

考慮到柔輪圓環的幾何形狀、載荷具有對稱性，假如沿水平直徑C1D1將圓環切開，由載荷的對稱性可知，截面C1和D1上的剪力為零，只有軸力和彎矩。利用平衡條件容易求出軸力大小等于F/2，而彎矩Mx屬于多余約束。由于圓環對于垂直直徑A1B1和水平直徑C1D1都是對稱的，所以只需要研究四分之一圓環，如圖3b。因為對稱截面A1和D1處的轉角等于零，可以把截面A1作為固定端，而把截面D1處的轉角為零作為變形協調條件。據此可以寫出力學的正則方程(限于篇幅，推導過程從略)，求得彎矩Mx= －Frm(0.5－1/π)，進一步得到柔輪圓環任意截面上的彎矩為

式中:F為波發生器對柔輪圓環的作用力;rm為柔輪圓環中性層變形前的圓半徑;φ為從水平截面D1起算的圓環截面的位置，φ=0～90°，逆時針為正。

由式(2)可以看出，柔輪圓環截面受到的彎矩大小與波發生器施加于柔輪的力F及圓環中性圓的半徑rm成正比，彎矩最大的位置在截面A1和B1處，所以此兩處屬于危險截面。

因為柔輪中心層橢圓長半軸方向和短半軸方向上的變形對剛輪、柔輪的嚙合影響最大，所以必須對柔輪圓環的垂直直徑A1B1和水平直徑C1D1的長度變化進行分析。

在一對F力作用下，柔輪圓環垂直直徑A1B1的長度變化，也就是F力作用點A1和B1的相對位移δAB。應用莫爾積分［5］沿整個圓環積分，可求得直徑A1B1的伸長量，即A1、B1兩點的相對位移 δAB為

式中:E為柔輪圓環材料的彈性模量;I為圓環截面對中性軸的慣性矩;EI為柔輪圓環的抗彎剛度，反映材料抵抗彎曲變形的能力。

考慮到慣性矩 I=bδ3/12，則

式中:b為柔輪圓環的軸向寬度;δ為柔輪圓環的厚度(也稱為柔輪的壁厚)。

柔輪圓環垂直直徑A1B1的長度伸長，水平直徑C1D1的長度必定是縮短的，應用莫爾積分，可求得C1、D1兩點的相對位移，即直徑C1D1的縮短量δCD為

由于δAB＞δCD，所以柔輪中性層上各點的徑向位移的最大值出現在力作用點處，柔輪的徑向最大變形量(參看圖2)為

柔輪變形前的分度圓直徑為dR=mZr，柔輪齒根高為hfR=，柔輪圓環體壁厚一般取［4］δ=(0.01 ～0.015)dR，本文取 δ=0.01dR。這里，m、Zr、分別是柔輪的模數、齒數和齒根高系數。根據通用諧波齒輪漸開線齒廓常用標準，對于α=20°，剛輪、柔輪都是正常齒時，齒根高系數按文獻［7］取=1.35。

若柔輪是標準齒輪(不變位)，則柔輪的中性圓半徑:rm=0.5dR－hfR－0.5δ，從而

在柔輪材料、柔輪圓環的軸向寬度確定以后，如果波發生器產生的力一定，則柔輪的徑向最大變形量W0將與(rm/δ)的三次方成正比，即

4 柔輪變形的敏感度分析

為了分析柔輪齒數對柔輪變形的影響，現提出柔輪變形的敏感度這個概念。

由前面的式(8)知道，柔輪徑向的最大變形量W0與(49.5－135/Zr)3成正比。所謂柔輪變形的敏感度，是指柔輪齒數改變時，柔輪徑向最大變形量W0如何變化。柔輪變形的敏感度并非表示變形量W0的絕對值，而是反映W0變化的態勢。式(8)表明，柔輪最大變形量對齒數的變化比較敏感。

應用MATLAB軟件的曲線繪制命令，根據式(8)可以畫出柔輪最大變形量的變化態勢與齒數之間的關系曲線，如圖4所示。從圖中可以看出，在柔輪齒數少于80時，隨著齒數的增加，變形量急劇增大，表明柔輪齒數的改變，對柔輪的變形影響特別明顯(很敏感)。當柔輪齒數大于100以后，柔輪齒數對變形量的影響逐漸減弱，變得不敏感了。特別是齒數超過200后，隨著齒數的增加對變形量的影響逐漸減小，且當齒數增加到一定值時，變形量基本上趨于恒定。

為了更清楚地看出柔輪齒數對變形的影響，我們對式(8)求Zr的導數，得柔輪徑向最大變形量W0的變動快慢(速率)為

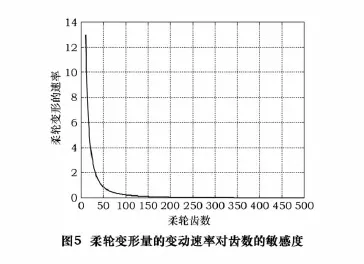
圖5是根據式(9)畫出的柔輪變形量的變動速率W01與齒數Zr之間的關系。從圖5中同樣可以得出與圖4類似的結論:柔輪齒數低于80時，齒數的改變引起的變形量的變化很大(很敏感);隨著齒數的增加，徑向變形量的變化速率迅速遞減。柔輪齒數超過200以后，變形量的變動處于平緩，齒數對變形量的影響就不敏感了，且當齒數大到一定值后，變形量基本上不再變化。

波發生器裝入柔輪之后，柔輪在強迫力的作用下發生彎曲變形，勢必在圓環內部產生應力，而應力與柔輪的變形程度有關。為了提高柔輪的工作壽命，必須減小柔輪的變形量，即在設計諧波齒輪傳動時，柔輪的齒數應當大于200，這也印證了為什么現有諧波減速器的柔輪齒數都較大。

柔輪的變形敏感程度也可以用柔輪中性層的曲率來衡量。將式(2)代入式(1)并考慮到I=bδ3/12，得到柔輪變形后中性層的曲率半徑為式中:φ是從水平截面D1起算的圓環截面的位置(參見圖3)，φ =0～90°，逆時針為正。

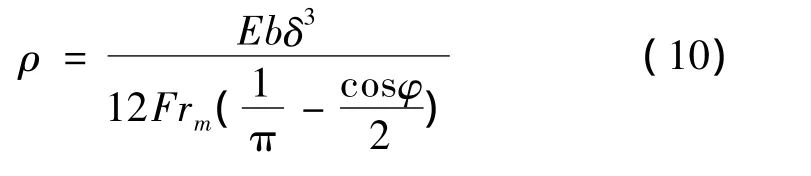
當柔輪材料、柔輪軸向寬度、壁厚、中性層半徑及波發生器對柔輪圓環的作用力確定以后，中性層的曲率半徑 ρ將與(1/π －0.5cosφ)成反比，即

根據式(11)可以畫出柔輪變形后曲率半徑與柔輪截面位置之間的關系曲線，如圖6所示。因為柔輪結構和變形受力的對稱性，只繪制了0°～90°的范圍(即1/4柔輪)。從圖6中可以看出柔輪變形后中性層的曲率變化情況:在角度區間為35°～65°時，柔輪中性層彎曲方向有變;當柔輪截面在50°這個角度附近，曲率半徑發生了突變(截面位置的改變引起的變形量的變化很敏感)，即柔輪的彎曲變形情況在此處，出現了圓環往外側彎曲向往內側彎曲的變化。在強度計算時，也應該把50°這個截面作為危險截面考慮。

5 結語

本文運用材料力學解決超靜定結構的方法，建立了環型柔輪初始變形量、截面彎矩的計算模型。通過對諧波齒輪傳動機構柔輪中性層變形規律的分析，可以得出以下結論:

(1)柔輪的徑向最大變形量與波發生器施加于柔輪的力F、柔輪中性圓半徑rm的三次方成線性關系。

(2)柔輪的齒數、模數、波發生器的結構決定了柔輪的變形規律及其疲勞強度，如果不是尺寸受限，柔輪齒數最好大于200。

(3)在波發生器作用力方向上柔輪的徑向變形量最大，此處齒根部容易出現應力集中，為危險截面位置;柔輪圓環位置角為 50°、130°、230°、310°的截面也應該作為危險截面考慮。

［1］陽培，張立勇，王長路.諧波齒輪傳動技術發展概述［J］.機械傳動，2005，29(3):69 －72.

［2］彭寶林，王華坤，柳勝.基于Abaqus的諧波齒輪環形柔輪變形仿真分析［J］.機械制造與自動化，2011，40(3):85 －88.

［3］辛洪兵.一種用于諧波傳動的浮動式波發生器:中國，200320103345.7［P］.

［4］饒振綱.行星傳動機構設計［M］.2版.北京:國防工業出版社，1994.

［5］劉鴻文.材料力學［M］.4 版.北京:高等教育出版社，2004.

［6］［蘇］沃爾闊夫，克拉伊聶夫.諧波齒輪傳動［M］.北京:電子工業出版社，1985.

［7］范又功，曹炳和.諧波齒輪傳動技術手冊［M］.北京:國防工業出版社，1995.