非對稱混合級聯型多電平逆變器調制方法研究

王鵬帥 韓如成

（太原科技大學電子信息工程學院，太原 030024）

級聯型多電平逆變器基于低壓小容量逆變器級聯的組合方式，技術成熟，易于實現，較適合七電平或九電平以上的多電平逆變器應用場合，具有易實現模塊化、易于擴展和調制方法簡單的優點。所以近幾年級聯型多電平逆變器在電機驅動、大功率有源電力濾波等場合得到了廣泛應用[1-3]。

傳統的 2H橋級聯型多電平逆變器，各單元直流電源電壓相等，各級聯單元采用相同的開關器件，在級聯的基本單元數目為N的情況下，其輸出的最大電平數為（2N-1），并且需要N個獨立的直流源。需要數目眾多的獨立直流源在一定程度上限制了級聯型多電平逆變器的應用范圍[4]。另一方面，當級聯數目為N時，需要的開關器件數目為4N，數目眾多的開關器件致使調制電路非常的龐大和復雜，所以如何簡化拓撲結構就成為多電平逆變器領域一個重點的研究方向。最近各國學者提出了幾種新型級聯型多電平逆變器拓撲[5-7]。

本文在新型拓撲電路的基礎之上，提出一種非對稱混合級聯型多電平逆變器拓撲電路，該拓撲電路結合混合型拓撲電路以及非對稱結構的優勢，充分發揮了不同類型開關器件的優勢和特點，減少了開關器件的使用從而簡化了調制電路。不同的拓撲電路只有搭配與之相適應的調制方法才能充分體現其優勢，國內外對于對稱型的拓撲電路調制方法研究已經相當成熟，如多載波正弦脈寬調制法、相移SPWM法、諧波消除法等，而非對稱型的拓撲電路調制方法的研究相對較少。但是不對稱的現象在很多場合都存在，比如：光伏并網重要環節的級聯式逆變器由于光伏電池的 V-I特性不同、接收光強的差異以及經過按MPPT算法后的DC/DC輸出等都會造成逆變器的直流源電壓等級的不同，即所謂的非對稱[8]。

由于存在上述問題，本文在一種新型非對稱混合級聯型多電平逆變器拓撲電路的基礎之上，提出一種與之相適應的調制方法。該方法兼具階梯波和正弦脈寬調制[9]的優點，充分發揮了新型拓撲電路的優勢。文章最后對提出的方法進行了仿真研究，驗證了該方法的正確性與有效性。

1 非對稱混合級聯多電平逆變器的拓撲及其工作原理

文獻[7]提出的新型拓撲結構如圖1所示，當直流源V1=V2=…=Vn，并且開關器件均采用如圖所示的IGBT時，該拓撲結構即為對稱型多電平逆變器。當V1≠V2≠…≠Vn，且各單元采用不同類型的開關器件時，該拓撲電路就稱為非對稱混合級聯結構，其工作原理和各開關狀態所對應的輸出電壓，見表1。

表1中輸出電壓為H橋部分開關器件t1和t2導通時的輸出，合理控制H橋部分的開關器件的通斷，就能實現對稱的反向電壓輸出。

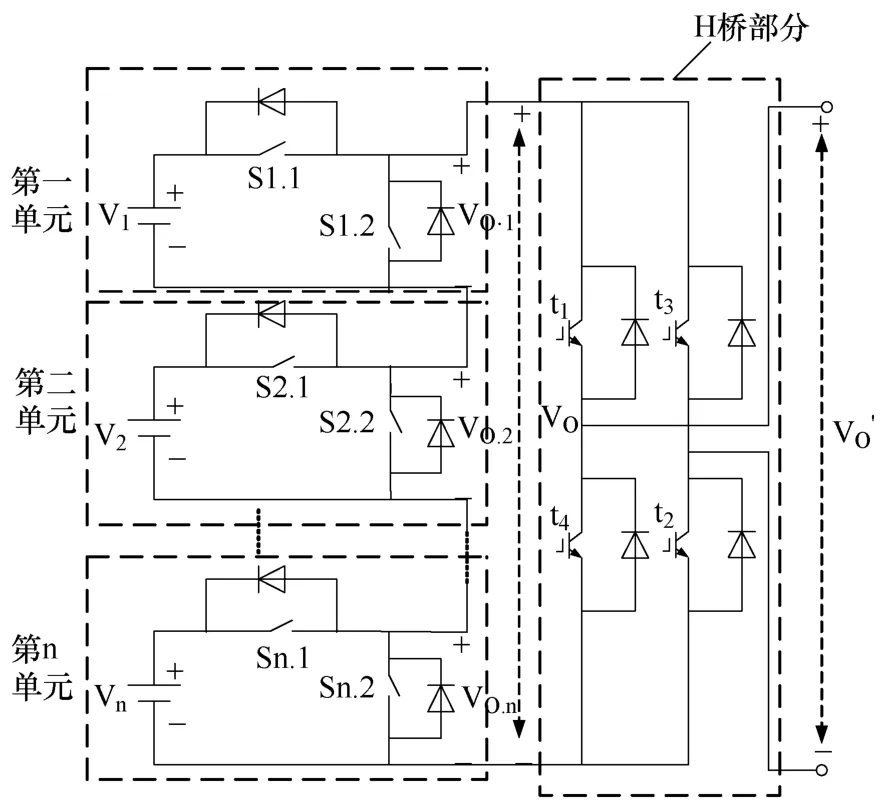
圖1 新型拓撲結構

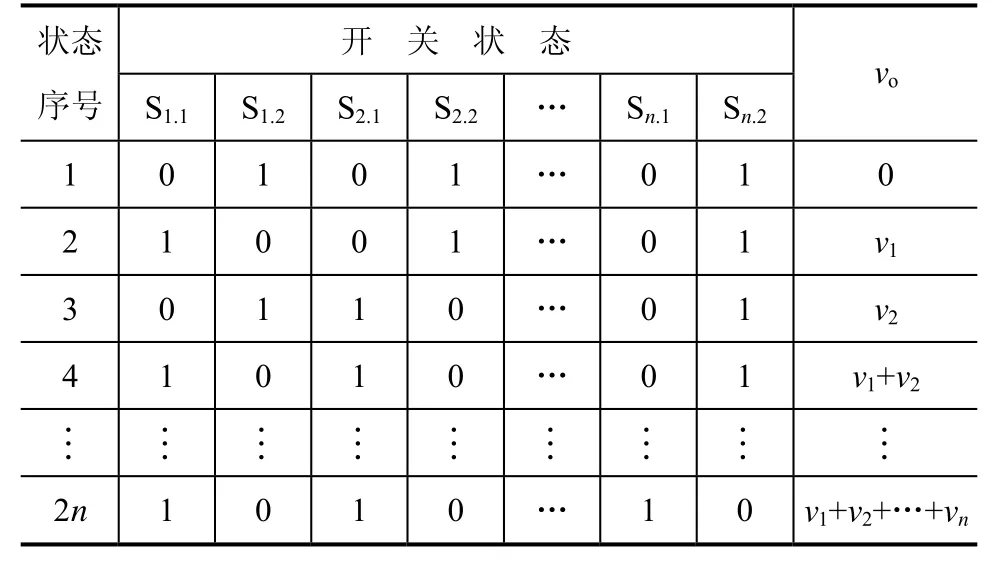
表1 基本單元級聯結構的輸出電壓Vo及其對應的開關狀態

如果令第一個直流電壓源v1為基準電壓，且

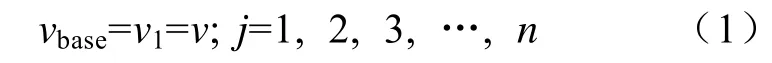
那么，這種級聯型逆變器就稱為對稱多電平逆變器，其最大輸出電壓可表示為

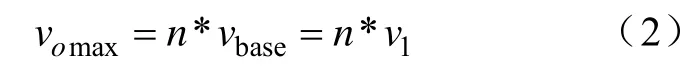
式中，n為H橋的個數，而其最多有效地輸出電平數為

不對稱的拓撲結構可以在不增加H橋數目的基礎上，增加輸出電壓的電平數。在文獻[7]中提出了一種不對稱多電平逆變器的電壓選取方案，其最大輸出電壓和電平數可由下式表示：

當vj= 2j-1v1，其中j=1, 2, 3, …, n

對應的最大打壓等級：

當vj= 2j-1v1，其中j=1, 2, 3, …, n

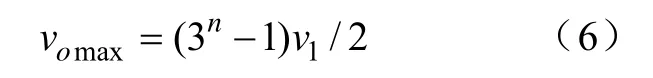
當vj= 3j-1v1，其中j=1, 2, 3, …, n

其對應的最大電壓等級：

當vj= 3j-1v1，其中j=1, 2, 3, …, n

當圖 1中的電路結構采用非對稱式的電路結構，并且開關器件采用不同類型的開關器時，該級聯型逆變器電路結構就稱為非對稱混合型多電平逆變器。

2 調制方法的研究

本部分通過二單元級聯與三單元級聯的拓撲電路來進行對上文中提出的非對稱混合級聯多電平逆變器的調制方法進行研究。

2.1 兩單元級聯

對于圖2中的兩單元級聯型拓撲結構，第一單元的開關器件采用GTO，第二個單元則采用IGBT，由于GTO具有更高的耐壓值，而IGBT則具有更高的開關頻率，所以第一個單元采用消諧波 PWM而第二單元采用SPWM，不同于傳統SPWM的地方是其調制波為正弦調制波us與第一單元的輸出電壓的波形之差，即

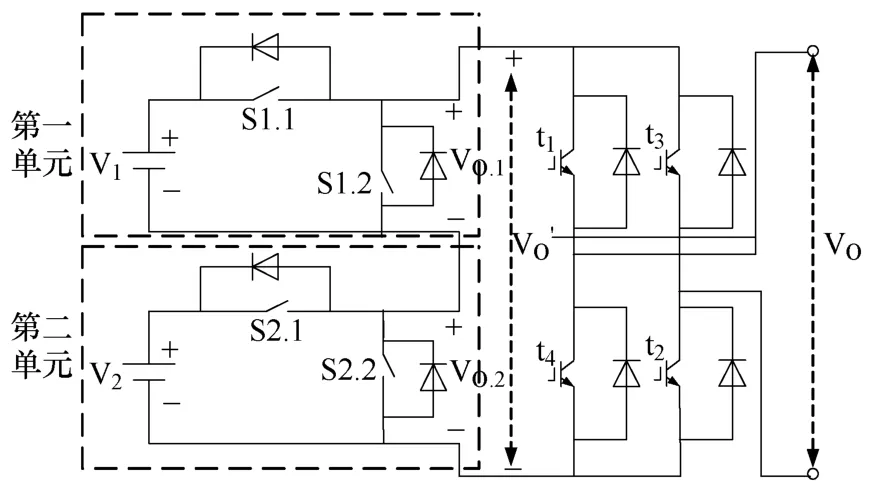
圖2 二單元級聯電路

其調制和輸出波形在0～π區間內的如圖3所示。

對第一單元的輸出電壓波形進行傅里葉分析可得

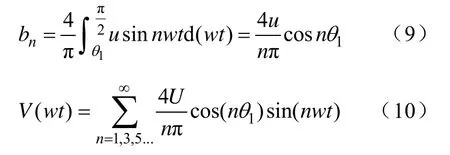
在n=5時，令cos（5θ1）=0，可以得到開關切換角θ1=π/10。

2.2 三單元級聯

對于圖4中的三單元級聯型拓撲結構，一單元和二單元均采用耐壓值較高的開關器件，如GTO，而第三單元則采用開關頻率較高的器件，如IGBT。

其調制方法為：第一單元采用固定觸發角驅動，以消除5次諧波，第二單元采用給定的觸發角驅動法，而第三單元采用高頻載波的SPWM控制法用來改善波形消除諧波。需要指出的是第三單元的調制波是正弦波us與一二單元的輸出電壓瞬時值波形之差的電壓波形 us=（up1+up2）。各個單元的輸出電壓up1、up2、up3的串聯疊加，就可以合成圖中所示的輸出電壓uo的波形。

圖4 三單元級聯電路

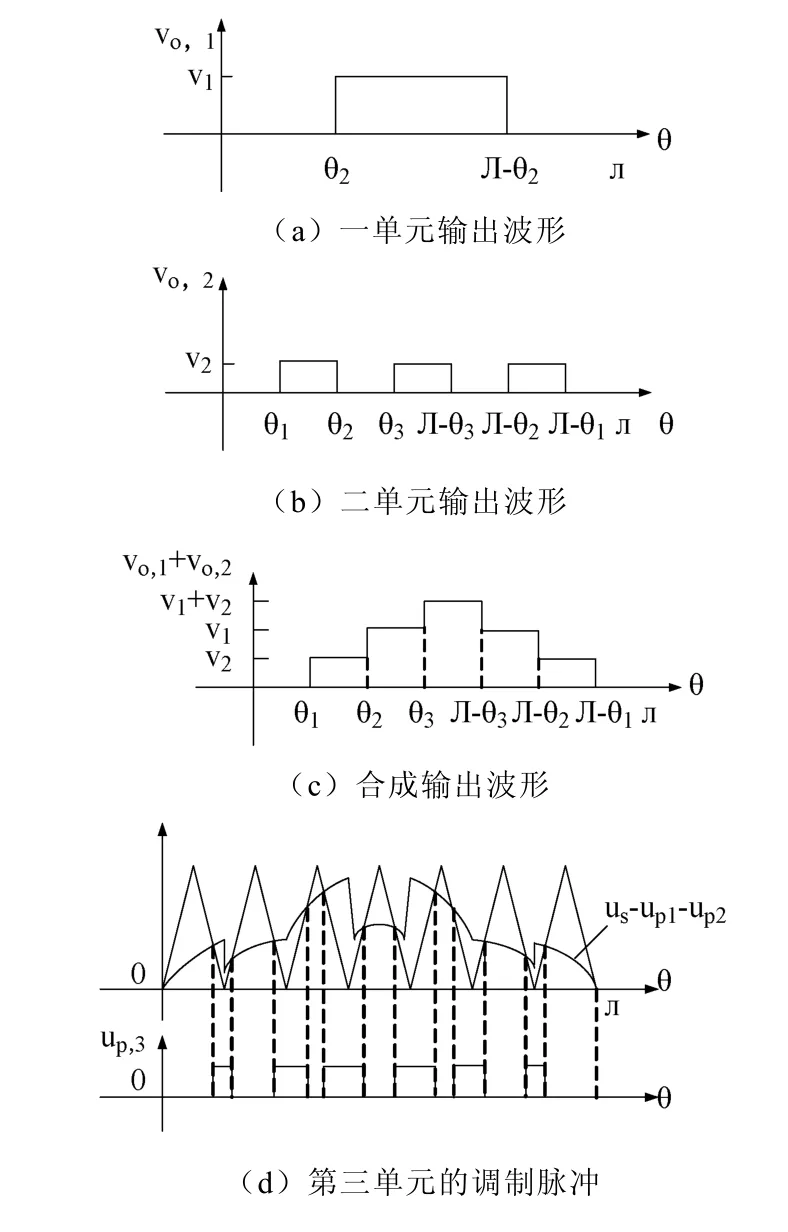
圖5 調制和輸出波形

圖5（c）中所示的輸出電壓波形的傅里葉級數展開為

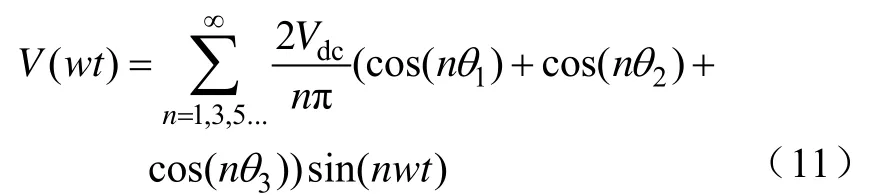
式中，n為一二單元輸出電壓所含有的諧波次數，理想情況下，給定的基波電壓V1，可以通過計算得出開關角θ1θ2θ3使高次諧波全部為零。這時V(wt)=V1sin(wt)。對于三相的多電平逆變器，每相中的三次諧波可以在線電壓中自動消除。本文要實現的目的是計算出基波電壓，并且消除5次和7次諧波。要解決的問題就是下面的式子：

3 仿真結果

在仿真軟件包Matlab/Simulink平臺上搭建了二單元和三單元非對稱混合級聯型多電平逆變器的模型，對本文中提出的調制方法進行了仿真驗證。仿真結果驗證了本文中提出的調制方法的正確性。

3.1 二單元級聯仿真

仿真參數：V1=3500V, V2=1500V，負載R=10Ω,L=0.01H，載波比：fc/fr=50，調制度 M=0.85，開關切換角：θ1=π/10。設置仿真時間為 0.04s，仿真結果如下。

仿真結果分析：從仿真結果可以看出，多電平逆變器的電壓輸出等級得到提高，同時5次諧波得到了很好的抑制。但是電壓波形受到影響，具有較多的高次諧波，不過諧波問題可以在增加級聯數目的條件下得到很好地解決。

圖6 二單元級聯仿真

這是一個有三個未知數的超越方程組。可以有很多種方法來得到這三個開關角，本文采用在Matlab中編寫m文件來計算得到。本文中定義調制比

3.2 三單元級聯仿真

仿真參數：V1=4000V, V2=2000V, V3=1000V，負載R=10Ω，L=0.01H，載波比：fc/fr=50。

設置調制度m=1.5，計算超越方程組：

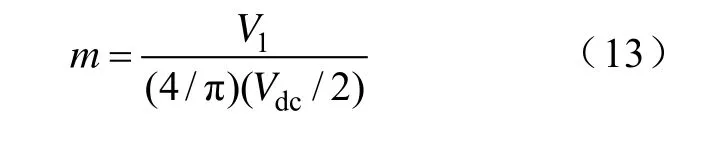
文獻[4]中關于超越方程組的分析，設置初始切換角度：θ1=40°, θ2=56°, θ3=80°，在 Matlab 中編寫 m文件，經過迭代計算可得：θ1=39.76°,θ2=55.99°, θ3=81.78°。設置仿真時間為 0.04s，仿真結果如圖7所示，從輸出波形頻譜圖7（b）中可以看出5次和7次諧波得到了很好的抑制。

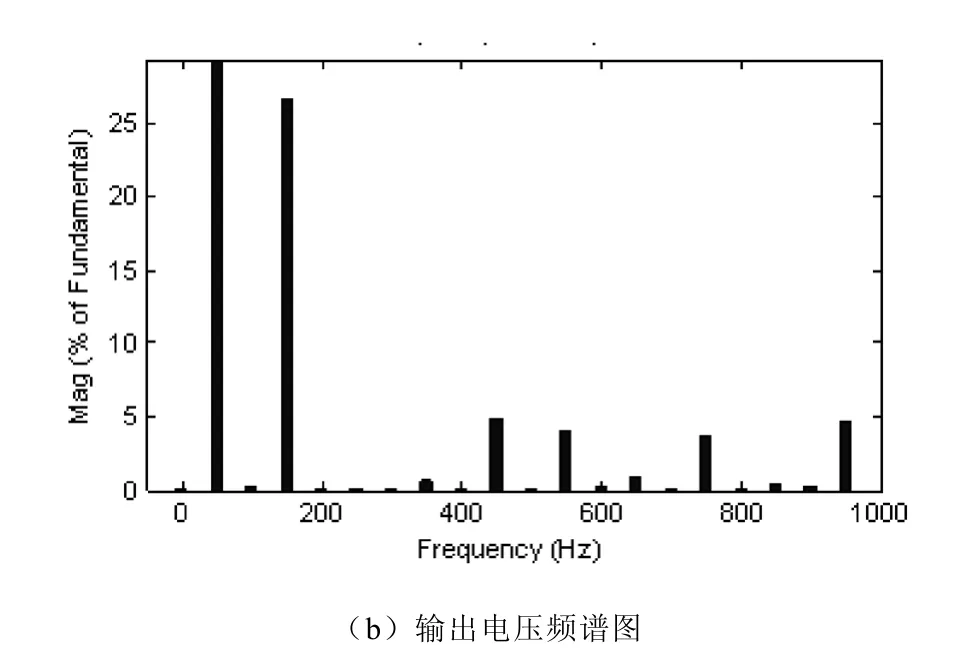
圖7 三單元級聯仿真

仿真結果分析：從3單元級聯結構的仿真結果可以看出，較2單元聯結構，輸出電壓的波形得到改善，減少了高次諧波的產生。同時可以看出，開關切換角的確定方法正確，5次和 7次諧波得到了很好的抑制，含量極少。

4 結論

本文在新型級聯型多電平逆變器的基礎之上，研究了非對稱混合級聯情況下該新型拓撲的調制方法。提出了階梯波和正弦脈寬調制相結合作用于該新型拓撲電路的思路，該方法充分發揮了不同開關器件的優勢，對非對稱的情況尤其適用，具有一定的應用價值。

[1] 劉風君,多電平逆變器技術及其應用[M].北京：機械工業出版社, 2007.

[2] TOLBERT L M, PENG F Z, HABETLER T G,Multilevel converters for large electric drivers[J].IEEE. Trans. on. Ind. Appl, 1999, 35(1)： 36-44.

[3] ZHANG D, TOLBERT L M, CHIASSON J N,OZPINECI B, LI H, Huang A Q： HYBRID CASCADED H-BRIDGES multilevel motor drive control for electric vehicles[C]. IEEE Power electronics specialiconference. Juju, Korea, 2006, 6：1-6.

[4] ZHONG D, TOLBERT L M, OZPINECI B, CHIASSON J N. Fundamental frequency switching strategies of a seven-level hybrid cascaded H-Bridge multilevel inverter[J]. IEEE in IEEE Transactions on Power Electronics. 2009, 24(1)： 25-33.

[5] BABAEI E. A cascade multilevel converter topology with reduced number of switches[C]. IEEE Trans Power Electron 2008, 23(6).

[6] HINAGO Y A Single-Phase multilevel inverter using switched series/parallel DC voltage sources. IEEE Transactions On IndustrialElectronics 2010, 57(8).

[7] BABAEI E, HOSSEINI S H. New cascaded multilevel inverter topology with minimum number of switches[J]. Energy Conversion and Management 2009(50)： 2761-2767.

[8] 陳元娣,劉滌塵,宋慶國.階梯波調制級聯逆變器觸發角的一種簡便算法[J].電工電能新技術, 2010, 29(1)：35-40.

[9] 費萬民,呂征宇,姚文熙.多電平逆變器特定諧波消除脈寬調制方法的研究[J].中國電機工程學報, 2003,23(9)： 11-15.